基于区间分析的发动机悬置系统稳健优化设计*

谢 展，于德介，李 蓉，吕 辉

(湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082)

前言

汽车发动机悬置系统是汽车的关键弹性支承元件，对汽车的平顺性、安全性和舒适性等有着重要影响。从被动隔振的角度看，它能隔离地面传递过来的低频振动，从而保证发动机稳定工作；从主动隔振的角度看，它能阻止发动机产生的振动向车架(车身)传递，从而降低车内振动与噪声。提高发动机悬置系统的隔振性能及其稳健性，对于提高整车的NVH性能具有重要意义。

针对参数不确定问题，研究人员已经提出了3种数学模型，即随机模型、模糊模型和区间模型。文献[1]中基于多目标优化与稳健设计理论，提出了一种汽车悬架系统的多目标随机优化方法。文献[2]中利用响应面法和区间分析方法构建悬置系统的优化模型，并采用连续二次规划方法对其进行优化。文献[3]中采用区间数学中的区间数描述悬置刚度的不确定性，提出了计算悬置系统固有频率和解耦率的区间分析方法。但目前悬置系统的不确定性研究均只针对悬置刚度，没有考虑悬置元件安装位置的不确定性，但是它对隔振性能的影响更明显[4]，设计中必须予以考虑。

本文中针对汽车发动机悬置系统参数的不确定性问题，基于区间分析理论，将稳健设计与多目标优化相结合，对发动机悬置系统进行稳健优化设计。在区间数学的基础上建立发动机悬置系统稳健优化模型，应用加权方法将多目标优化转化成单目标优化，以克服多目标优化的计算困难；采用多层次遗传算法解决稳健优化模型中的优化嵌套问题。悬置系统传递到车身的动反力大小直接表征了系统隔振性能的优劣，动反力的波动过大不但达不到优化的目的，而且会影响发动机的工作性能。为兼顾动反力的优化及其稳健性，该方法以动反力及其变化范围最小为目标函数，即悬置系统优化性能的评价标准，以固有频率的合理配置为约束条件，以悬置刚度为设计变量，并考虑悬置系统参数的不确定性，将悬置刚度和悬置位置的变化范围设为区间参数，对悬置系统进行优化，达到良好的效果。

1 悬置系统的固有频率和动反力

1.1 悬置系统的动力学模型

汽车发动机悬置系统的固有频率一般在30Hz以下，而汽车动力总成各部分的一阶弹性模态频率一般都在60Hz以上，两者相差甚远。因此，在对悬置系统进行隔振降噪优化时，发动机和车架可以被视为刚体。于是，汽车发动机在空间中的运动具有6个自由度，即沿3个相互垂直的轴线方向的往复直线运动和绕此3根轴线的回转运动，这样发动机悬置系统有6个振动模态以及相应的6个固有频率。悬置系统的6自由度动力学模型[5]如图1所示。

根据拉格朗日方程，6自由度汽车发动机悬置系统的振动微分方程为

(1)

其中{X}=(xyzθxθyθz)

式中：{X}为系统的广义坐标；[M]为系统的质量矩阵；[K]为系统的刚度矩阵；[C]为系统的阻尼矩阵。

由于橡胶悬置元件的阻尼很小，且对固有频率影响不大，所以阻尼可以忽略不计。因此式(1)可以改写为

(2)

根据以上汽车发动机悬置系统动力学模型，在测得发动机的总质量、转动惯量和惯性积以及各悬置的刚度、安装位置和角度后，便可求得发动机悬置系统的模态参数。

1.2 悬置系统的固有频率配置

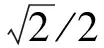
(3)

式中：i为气缸数；n为发动机转速；τ为冲程数。

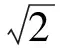
另外，从避免共振的角度来看，要求对系统的固有频率进行合理配置。发动机悬置系统的各阶振动频率应有一定间隔，一般要求最小差值在1Hz左右[6]。

1.3 悬置系统的动反力

汽车发动机在怠速工况且不考虑阻尼的情况下，悬置系统的强迫振动微分方程为

(4)

式中：{Fe}为系统所受的简谐激励力矢量。

悬置系统受迫振动的稳态解为

{Udyn}=([K]-ω2[M])-1{Fe}

(5)

于是，第i个悬置传递给车身的动反力[5]为

{fi}={-[ki] [ki][ri]}{Udyn}

(6)

式中：[ki]为第i个悬置在全局坐标系中的刚度矩阵；[ri]为第i个悬置位置坐标的反对称阵。

因此，怠速工况下悬置系统传递给车身的总动反力为

(7)

式中：fxi、fyi、fzi为第i个悬置在怠速工况下动反力的3个分量。

作为汽车的最主要振源，发动机传递到车身的动反力大小是悬置系统隔振性能的直接指标，其值越低则表征系统隔振性能越好。此外，动反力的波动范围过大会使发动机工作环境不稳定，影响发动机的工作性能，故应控制动反力的波动范围。

2 基于区间分析的稳健优化设计

在汽车发动机悬置系统的确定性优化设计中，相关参数和设计变量都是确定性数值，其优化模型为

(8)

式中：f(X)为目标函数；gi(X)为约束函数；n为约束的个数；X为悬置刚度；S为设计空间。

然而，在工程实际中，汽车零部件在生产制造、安装使用和汽车行驶环境中都存在着大量的不确定性。而参数的细微偏差或波动则可能导致系统性能大的波动，甚至导致系统失效。因此，在悬置系统的优化设计过程中，必须考虑悬置参数的不确定性而进行稳健设计。稳健设计通过调整变量的取值及其容差，使系统性能在参数发生一定变动的情况下仍能满足设计要求。与确定性优化相比，稳健设计进行了不确定性分析，更好地反映了悬置元件的实际情况，使悬置系统的设计与工程实际相吻合。针对参数的不确定性问题，区间理论近年来得到了广泛的关注。由区间理论建立的汽车发动机悬置系统不确定性优化模型为

(9)

式中：f(X,U)为目标函数；gi(X,U)为约束函数；n为约束的个数；U为表示悬置位置的区间参数；UL和UR分别为区间参数的上下限；X为悬置刚度，取为设计变量；S为设计空间。

在式(9)中，目标函数和约束由于区间参数设计变量的不确定性，其取值也是一个区间。文献[7]中根据序关系提出：在工程实际中，不但要求目标函数的设计目标值要小，且要求其取值范围也要小。因此，目标函数应为

(10)

其中

(11)

式中：m(f(X,U))为目标函数的设计目标值；w(f(X,U))为目标函数的取值区间；fR(X,U)与fL(X,U)分别为目标函数取值的上下限。

由式(10)和式(11)，式(9)所示的不确定性优化问题可转换成一个多目标的确定性优化问题。对于多目标优化问题，直接进行优化会给计算带来困难，必须对其进行相应的处理。本文中采用加权法，即将多目标优化问题通过加权转化成单目标优化问题，以便于优化计算。加权处理后的汽车发动机悬置系统不确定性稳健优化模型为

(12)

式中：X为悬置刚度；XL与XR为悬置刚度取值的上下限；α为加权系数，其取值范围为0～1。

从式(10)可知，基于区间分析的不确定性优化问题，既要求得目标函数的目标值，也要求得目标函数的最小值，这就产生了优化嵌套问题。本文中采用遗传算法对稳健优化模型进行多层次全局优化计算，以稳健优化模型的目标函数为遗传算法的适应度函数，其寻优过程分为两步：首先，以悬置刚度为设计变量，在其设计空间内产生第一层次初始种群；然后，以第一层次初始种群中的个体和悬置位置参数为区间变量，在其变化区间内产生第二层次初始种群代入适应度函数计算；最终，通过上述迭代寻优计算得到稳健可靠的优化解。

基于区间分析的汽车发动机悬置系统稳健优化设计流程如图2所示。

3 数值算例

对图1所示的某轿车发动机悬置系统进行稳健优化设计，该车发动机的布置方式是斜置式，并采用四点支撑方式。悬置系统的设计参数有悬置刚度、位置和安装角度，但由于悬置位置和安装角度涉及到整车尺寸设计，不易做出调整，因此选择悬置刚度作为设计变量(共12个)，悬置位置(共12个)作为区间参数进行优化。优化前发动机悬置系统的刚度值和惯性参数值分别如表1和表2所示。

表1 优化前各悬置的静刚度值 N/mm

表2 发动机悬置系统的惯性参数值 kg·mm2

该车发动机为直列式四缸四冲程发动机，怠速转速为900r/min，主要激励力为2阶往复惯性力，根据式(3)计算得其激励频率为30Hz。从隔振的角度出发，根据1.2节可算得悬置系统固有频率的取值范围应为4～21Hz。从避免共振的角度出发，各阶固有频率之间的差值应在1Hz以上。以悬置系统固有频率的合理配置为优化模型的约束条件，可表示为

(13)

本文中以动反力及其波动范围最小为目标函数，考虑到悬置刚度不能太“软”也不能太“硬”，其取值区间为50～305N/mm，则悬置系统的确定性优化模型为

(14)

考虑到悬置元件由于生产制造、安装和测量过程中的不确定性，取位置参数的变化范围为5mm,并且取加权系数为0.5，则悬置系统的稳健优化模型可表示为

(15)

对悬置系统初始模型进行模态参数和动反力计算，结果如表3所示。由表可见：1阶与2阶、3阶与4阶固有频率很接近，差值小于1Hz，从1.2节的分析可知，悬置系统容易发生共振；且悬置系统的动反力比较大，达到了287.28N；动反力的波动区间亦较大，变化范围为48.33N。因此，须对此悬置系统进行优化。

悬置系统确定性优化后各悬置的静刚度值如表4所示，优化后的结果如表3所示。从表3可知，优化后系统各阶频率之间的差值增大，都在1Hz以上，符合频率合理配置的要求；动反力也得到较大改善，最小值只有185.10N，降幅达到了35.6%。但若考虑到悬置刚度的不确定性，假定其变化范围为其优化值的10%。在这个波动范围内，对悬置系统的动反力进行稳健性分析，计算得到其变化区间为[184.87,253.96]，波动幅度达到了最优值的37.3%，说明即使不考虑悬置位置的不确定性，确定性优化结果的稳健性也很差。因此，须对此悬置系统进行稳健优化设计。

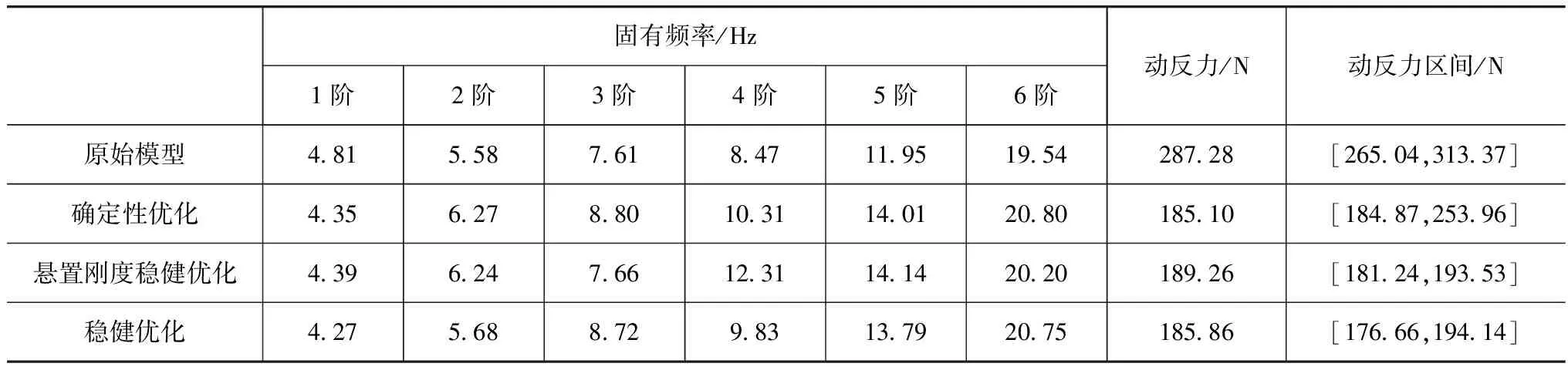
表3 悬置系统优化前后参数对比

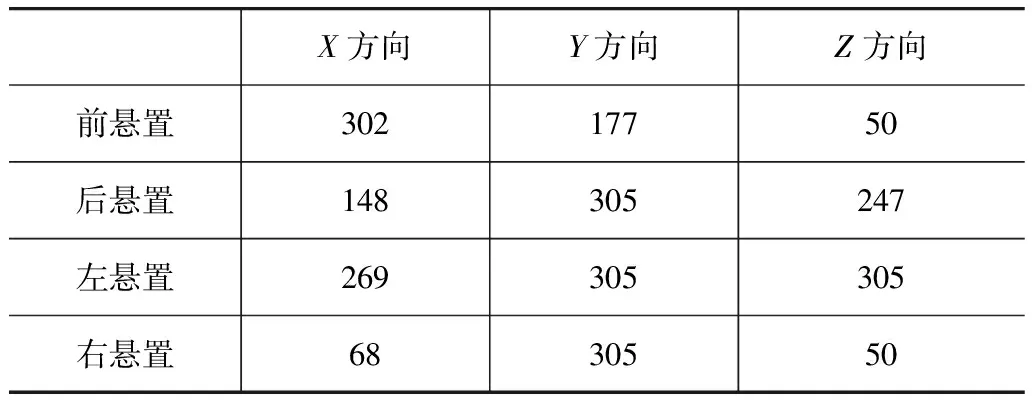
表4 确定性优化后各悬置的静刚度值 N/mm

稳健优化后的静刚度值如表5所示，优化后的结果如表3所示。从表3可知，优化结果满足频率合理配置要求，且动反力的变化范围降至最优值的6.49%，稳健性得到了提高，但动反力有一定的增大。若考虑悬置位置在5mm的范围内波动，得到动反力的变化区间为[178.52,203.41]，动反力的变化范围为其最优值的13.2%，比刚度稳健优化设计的动反力变化区间大一倍多。可见，悬置位置参数对悬置系统的影响比悬置刚度要明显。因此，须同时考虑悬置系统的悬置刚度和悬置位置参数的不确定性。

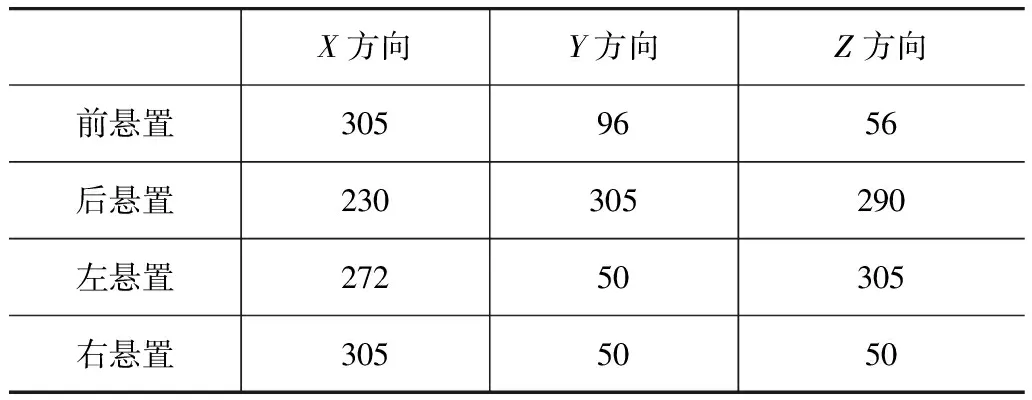
表5 刚度稳健优化后各悬置的静刚度值 N/mm

由于汽车发动机悬置位置参数是通过测量得到的，且悬置系统并不是在一个静态的环境中工作，因此必须考虑二者引起悬置位置参数的不确定性，假设悬置系统位置参数取值在测量值附近的变化范围为5mm。另外由于悬置元件的不确定性，其刚度值也会有一定的波动，假设其变化范围为目标值的10%。根据式(15)算得优化后的各悬置的静刚度值如表6所示，优化后系统固有频率及动反力结果如表3所示。从表3可知，优化后系统固有频率满足合理配置的要求；与悬置刚度稳健优化的结果相比，其动反力目标值进一步降低，且其变化区间也进一步缩小，其波动幅度为目标值的9.4%，稳健性得到了提高，满足稳健设计要求。

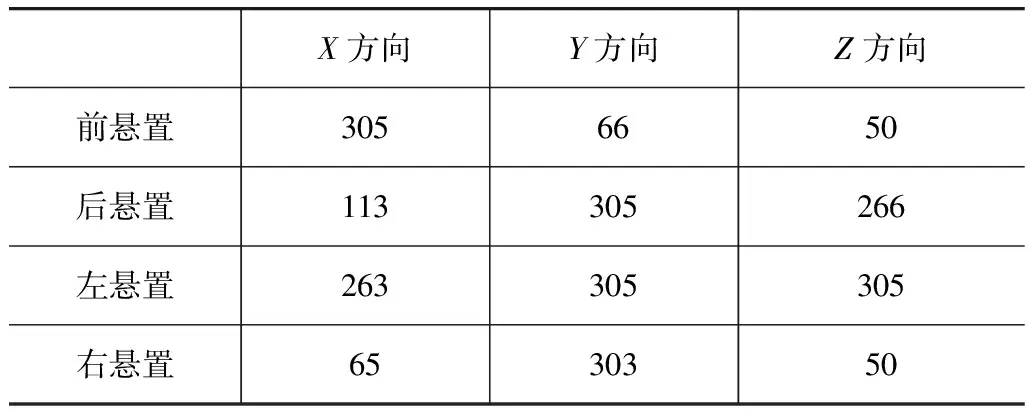
表6 稳健优化后各悬置的静刚度值 N/mm

4 结论

(1) 在区间分析理论的基础上，将稳健优化设计与多目标优化设计相结合，应用遗传算法，对悬置系统进行稳健优化设计。该方法在对悬置刚度进行寻优的同时，还考虑了悬置刚度和悬置位置参数的不确定性，从而在实现优化的同时提高了悬置系统优化结果的稳健性。

(2) 对某轿车的发动机悬置系统进行稳健优化设计，结果表明：在固有频率满足合理配置要求的同时，稳健优化设计不仅大幅降低了悬置系统的动反力，且动反力的变化范围也明显缩小，说明该方法能有效用于悬置系统的优化设计。

[1] Massimiliano Gobbi,Francesco Levi,Giampiero Mastinu.Multi-objective Stochastic Optimization of the Suspension System of Road Vehicles[J].Journal of Sound and Vibration,2006,290(3-5):1055-1072.

[2] 包健,成艾国,何智成,等.区间响应面悬置固有频率匹配研究[J].噪声与振动控制,2011,31(2):21-24.

[3] 吴杰,周胜男.动力总成悬置系统频率和解耦率的稳健性优化方法[J].振动与冲击,2012,31(4):1-7.

[4] 刘丹,侯之超.动力总成悬置设计中惯性参数的灵敏度分析[J].汽车工程,2007,29(10):884-888.

[5] 周冠南,蒋伟康,吴海军.基于总传递力最小的发动机悬置系统优化设计[J].振动与冲击,2008,27(8):56-58.

[6] 樊逸斌.基于灵敏度分析的悬置系统设计及优化[J].上海汽车,2010(6):17-20.

[7] Jiang C,Han X,Liu G R,et al.A Nonlinear Interval Number Programming Method for Uncertain Optimization Problems [J].European Journal of Operational Research,2008,188(1):1-13.

[8] 吴杰.区间参数振动系统的动力优化[J].力学学报,2003,35(3):373-376.

[9] 翁建生,张斌,汪洋.汽车动力总成的区间模糊多目标优化[J].现代车用动力,2006(3):28-31.

[10] Hiroshi Ito,Hiromitsu Ohmori,Akira Sang.Analysis of Robust Performance with Multiple Objectives[J].Systems and Control Letters,1995,25(2):141-149.

[11] Jiang C,Han X,Guan F J,et al.An Uncertain Structural Optimization Method Based on Nonlinear Interval Number Programming and Interval Analysis Method[J].Engineering Structures,2007,29(11):3168-3177.

[12] David Moens,Dirk Vandepitte.Interval Sensitivity Theory and Its Application to Frequency Response Envelope Analysis of Uncertain Structures[J].Computer Methods in Applied Mechanics and Engineering,2007,196(21-24):2486-2496.