基于相平面法的制动方向稳定性分析*

李 静，王子涵,2，王宣锋

(1.吉林大学,汽车仿真与控制国家重点实验室，长春 130022； 2.上海泛亚汽车技术中心有限公司,上海 201201;3.中国第一汽车集团技术中心,长春 130011)

前言

制动方向稳定性是指在制动过程中，汽车按驾驶员给定的轨迹行驶的能力，即维持直线行驶或按预定弯道行驶的能力[1]，对车辆安全具有重要影响，本文旨在评价分析汽车制动方向稳定性，完善制动方向稳定性的评价方法。

目前，较多学者从整车特征参数时域角度对制动方向稳定性展开研究，如文献[2]中对转向制动的研究和文献[3]中对差动制动稳定性的研究，它们均应用如横摆角速度、质心侧偏角等整车参数的时间历程曲线对制动稳定性进行定性分析，但也仅局限于定性评价。

文献[4]中在前轮转向控制研究中应用了质心侧偏角-横摆角速度相平面，该类相平面通常用于转向稳定性分析，较好地反映了转向稳定域，但其稳定域受车速影响较大，不适用于速度实时变化的制动稳定性分析；文献[5]中基于大量实验提出β相平面稳定域，实现制动稳定性分析和判断，该类相平面随速度变化相对较小，可用于制动稳定性分析，但未明确提出稳定域边界函数的判定方法；文献[6]中针对β-r相平面，通过求解2自由度模型稳定点和相轨迹的向前合并与向后合并，得到了该类相平面的稳定域；同时，文献[7]中通过神经网络和遗传算法提出一种得到稳定边界的方法，但较为复杂。除此之外，文献[8]中提出能量相平面方法，用于分析两轴车操纵稳定性，通过能量相平面表征了诸如侧向能量、转向瞬态半径等运动特性变化规律。

结合以上研究，本文中基于两轴汽车Simulink模型，应用β相平面和能量相平面法进行制动方向稳定性分析，并针对β相平面，提出基于鞍点和初始稳定相点分布的稳定域边界计算方法。

1 7自由度动力学模型

为分析制动方向稳定性，须分别计算各轮纵向力与侧向力。因此，本文中建立了7自由度动力学模型，包括整车3自由度和4个车轮转动自由度，既考虑了侧向运动，又考虑了纵向运动，全面分析了整车运动状态。

建立动力学模型之前，作如下假设：忽略空气阻力，认为汽车只做平行于地面的平面运动；假设轮胎滚动阻力矩为一定值，并且没有轮胎变形引起的回正力矩，车轮半径为定值，将每个车轮简化为具有转动惯量、只有转动的单自由度系统；不考虑载荷的转移，制动器简化为理想的1阶惯性元件。

图1为整车受力分析图，包含建模所用的3种坐标系：地面固定坐标系OXYZ、车辆坐标系oxyz和轮胎坐标系owxwywzw。其中车辆坐标系的原点位于车辆质心o，x轴位于车辆的纵向对称平面内，且指向前进方向为正向，规定y轴正向指向驾驶员左侧，指向上方规定为z轴正向；规定轮胎坐标系xw轴在车轮中分平面与水平地面的交线上、且指向前进方向为正，规定xw轴与车轮旋转轴线在水平地面投影线的交点为轮胎坐标系的原点ow，yw轴位于水平地面内、且规定面向xw正方向时、指向左侧为yw轴正方向，规定指向上方为zw轴正方向。

1.1 整车模型

假设整车模型包括簧载质量、前非簧载质量和后非簧载质量3部分。整车的3个自由度为纵向速度u，侧向速度v和横摆角速度r。经过化简，得整车模型计算公式为

(1)

(2)

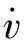
(3)

式中：mf、mr为前、后轴非簧载质量，kg；Izzf、Izzr为前、后轴非簧载质量横摆转动惯量，kg·m2；Iz为通过车身质心关于z轴的转动惯量，kg·m2；u为整车质心纵向速度，m/s；v为整车质心侧向速度，m/s；r为整车横摆角速度，rad/s；lf、lr为前、后轴中心到质心的距离，m；mb为簧载质量，kg。且Qu、Qv、Qr分别为对应自由度u、v和r的广义力，N，公式为

Qu=(Fxw1+Fxw2)cosδf-(Fyw1+Fyw2)sinδf+Fxw3+Fxw4

(4)

Qv=(Fxw1+Fxw2)sinδf+(Fyw1+Fyw2)cosδf+Fyw3+Fyw4

(5)

[(Fxw2+Fxw1)sinδf+(Fyw1+Fyw2)cosδf]lf+

(6)

式中：Fxwi为第i轮纵向力，N；Fywi为第i轮侧向力，N；δf为转向轮转角，rad；af为前轴轮距，m；ar为后轴轮距，m。

1.2 制动器模型

制动器模型指制动器力矩与制动压力间的关系，假设制动器为理想元件，则制动方程为

Mbi=ki·Pi

(7)

式中：Mbi为第i轮制动力矩，N·m；ki为第i轮制动器制动因数,N·m/kPa；Pi为第i轮制动压力，kPa。对于制动压力到制动力转换环节，在此简化为一个带迟滞的1阶惯性环节，传递函数为

(8)

式中Km和Tm为制动器参数。

1.3 轮胎滚动动力学模型

对车轮进行受力分析，如图2所示。建立车轮转动动力学模型，输入为车轮的纵向力Fxwi、制动力矩Mbi；输出为各轮角速度ωi。其中i=1、2、3、4分别代表不同车轮。

根据牛顿第二定律对每个车轮列动力学平衡方程，得出车轮转动的动力学方程为

(9)

式中：rdi为第i轮的滚动半径，m；Iwi为第i轮绕轮心的转动惯量，kg·m2。

1.4 轮胎模型

在此，轮胎模型采用GIM轮胎模型，输入为各轮胎坐标系下的轮心纵向线速度uxwi、车轮转动角速度ωi、侧偏角βwi和垂向载荷Fzi，输出为各轮所受纵向力Fxwi和轮胎侧向力Fywi。其中uxwi、侧偏角βwi通过车辆平面运动分析得到。

基于上述动力学和运动学分析，建立包含ABS系统的2自由度整车动力学模型如图3所示。

2 应用于制动方向稳定性的β相平面及其稳定域边界函数

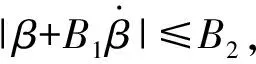
为便于非线性方程求解[11]，通过简化目标车得到2自由度模型，求解非线性方程鞍点和结点。基于鞍点和相平面稳定初始相点分布图，得到相平面稳定域边界函数，用于制动方向稳定性的分析。

为简化动力性模型，便于绘制相平面，简化的2自由度模型示意图如图4所示，其动力学方程为

(10)

式中：Izz为整车相对oz轴转动惯量，kg·m2；m为整车质量，kg；Fyf为前轮侧向力，N；Fyr为后轮侧向力，N；其余参数与7自由度模型相同，且

结合以上公式，并简化得

(11)

(12)

轮胎受力Fyf和Fyr通过GIM模型计算。通过式(11)和式(12)求稳定点，包括结点和鞍点，稳定点即对应式(11)和式(12)右侧为0。对于β相平面的平衡点求解应满足如下关系式：

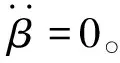
图5为β相平面及其奇点分布图，图中星点表示式(11)和式(12)所求在合理范围内的结点(中间的稳定点)和鞍点(两端的不稳定点)。

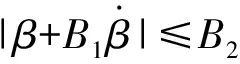
3 制动方向稳定性的能量相平面分析

能量相平面的分析机理为通过车辆转向动能与前进动能之比表征车辆方向稳定性。制动失稳时，产生侧向滑移等失稳现象会导致侧向能量的增大。根据前述动力学方程，可得总能量为

(13)

式中：ms为车辆总质量，kg；Izs为整车对z轴转动惯量，kg·m2。沿坐标系纵轴ox的纵向动能为ETrx：

(14)

沿oy轴的侧向动能为ETry：

(15)

侧向能量和纵向能量之比为

(16)

(17)

分别以v/u为横坐标、ρr/u为纵坐标做出能量相平面图，在一定初始条件下开始仿真，绘成的曲线看成是一种相平面曲线，该曲线上任意一点T，其坐标值为(x，y)，对应的向量oT的模代表了转向能量相对前进能量的水平，从能量的角度对运行过程中侧向能量进行表述，进而说明是否失稳。

转向时瞬心半径rds基本满足关系rds·r=u，且能量相平面纵坐标为ρr/u，则纵坐标与转向瞬心半径成反比关系，结合相平面纵坐标可进行转向情况的表征。

4 制动方向稳定性的能量相平面分析

为验证能量相平面和β相平面评价制动方向稳定性效果，进行了极限工况转向制动仿真，通过制动轨迹、能量相平面和β相平面对不同工况制动方向稳定性进行评价。仿真工况包括：(1)无ABS时，高/低附着路面转向制动；(2)有/无ABS低附着路面转向制动运动。

一方面通过无ABS系统时高低附着路面转向制动，再现转向制动无失稳与失稳工况，验证相平面法对于制动方向稳定性表征的有效性；另一方面通过低附着路面有/无ABS转向制动，验证控制算法对制动方向稳定性的作用。

4.1 高低附着路面转向制动

仿真工况为无ABS系统高低附着路面转向制动。高附着路面附着系数为1.0，低附着路面附着系数为0.2，初始制动车速为60km/h，转向盘转角为1.4rad。仿真结果如图7～图9所示。

由图7可知，高附着路面车辆可较好地按照驾驶员意图实现转向制动，而低附着路面车辆几乎无法实现转向动作。由图8可见，每个圆形虚线表明一个能量级，能量级越大对应侧向能量相对纵向能量比例越大，稳定性越差。表1为能量相平面数据表，可定量进行制动方向稳定性分析。结合图表可知，低附着路面侧向能量与纵向能量比值大约为高附着路面的5倍，且由纵坐标可知，低附着路面转向半径小于高附着路面，无法保证车辆转向能力。

表1 高/低附着能量相平面数据表

由图9可知，低附着路面的相轨迹越过稳定域边界，进入非稳定区域，进一步表明已失去制动方向稳定性，而高附着路面仍保持在稳定区域内。

4.2 低附着路面有/无ABS系统转向制动

4.2.1 基于PID控制的ABS控制器

制动方向稳定性的准确评价可提高相关控制策略的有效性。为验证相平面分析方法对控制算法的评价效果，建立了基于PID控制的ABS控制器[12]，完成有/无ABS控制器低附着路面转向制动方向稳定性评价。

PID控制器是利用设置给定的目标值和实际控制输出值的偏差，对控制对象进行的一种控制，如图10所示，以目标滑移率s0和实际滑移率sx之差为控制偏差e，即e=s0-sx，通过对其进行比例放大、微分放大和积分放大，进行制动压力的调节进而实现滑移率的良好控制，其控制规律为

(18)

式中：pi为第i轮制动压力；KP为比例系数；KI为微分系数；KD为积分系数。在离线仿真模型的基础上，通过大量实验实现了3个参数的匹配。

4.2.2 低附着路面有/无ABS转向制动仿真分析

基于7自由度整车模型和PID控制的ABS控制器，进行低附着路面有/无ABS转向制动稳定性评价。仿真工况为：低附着路面(附着系数为0.2)，初始制动车速为60km/h，转向盘转角为1.4rad。仿真结果如图11～图13所示。

由图11可知，有ABS系统制动过程与高附着路面制动过程类似，可按驾驶员意图完成转向动作。

同图8，图12中每个圆形虚线表明一个能量级，能量级越大对应侧向能量相对纵向能量比例越大，稳定性越差。表2为有/无ABS转向制动能量相平面数据表，可定量进行制动方向稳定性分析。结合图表可知，无ABS时侧向能量与纵向能量比值大约为有ABS时的3.4倍，且由纵坐标可知，有ABS时转向半径较无ABS时小。

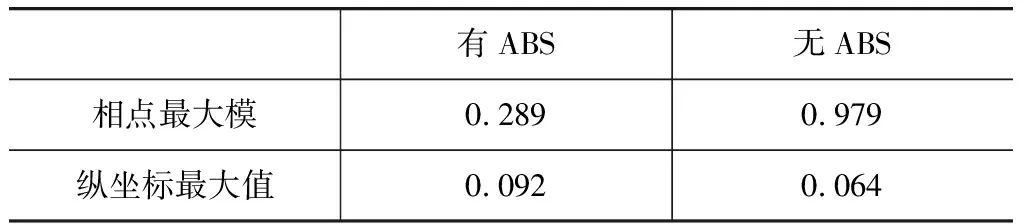
表2 有/无ABS能量相平面数据表

图13为有/无ABS转向制动时β相平面图。由图可见，无ABS时系统很快失稳，进入非稳定区域，而有ABS时，相轨迹随着ABS作用，重新回到稳定区域，表明ABS控制保证轮胎附着力，进而起到了提高制动方向稳定性的功能，验证了β相平面对ABS评价的有效性。

5 结论

(1) 基于Matlab/Simulink搭建了7自由度整车模型和ABS控制器，应用相平面法对制动方向稳定性进行定量分析与评价，所用相平面法包括能量相平面和β相平面。

(2) 针对β相平面，基于鞍点与初始稳定相点提出稳定域与非稳定域边界函数的求解方法。

(3) 基于以上模型和分析方法，通过有/无ABS和高/低附着下的离线仿真，验证了相平面法定性判断和定量分析制动方向稳定性的可行性和有效性。

[1] 刘翔宇,陈无畏.基于DYC和ABS分层协调控制策略的ESP仿真[J].农业机械学报,2009(4):1-6.

[2] Dahlberg E. Yaw Instability Due to Longitudinal Load Transfer During Braking in a Curve[J]. Intelligent Transport Systems (ITS) Research and Applications, SP-1467,1999.

[3] Chen N, Zhang B J, Zhong G H. Enhancements in Vehicle Stability with Yaw Moment Control via Differential Braking[C]//Vehicular Electronics and Safety (ICVES),2009 IEEE International Conference on. IEEE,2009:136-140.

[4] Ono E, Hosoe S, Tuan H D. Bifurcation in Vehicle Dynamics and Robust Front Wheel Steering Control[J]. Control Systems Technology, IEEE Transactions on,1998,6(3):412-420.

[5] Koibuchi K, Yamamoto M, Fukada Y, et al. Vehicle Stability Control in Limit Cornering by Active Brake[J]. Training,1996,2008:06-23.

[6] Ko Y E, Lee J M. Estimation of the Stability Region of a Vehicle in Plane Motion Using a Topological Approach[J]. International Journal of Vehicle Design,2002,30(3):181-192.

[7] Akihiko Shimura, Kazuo Yoshida. Rule Extraction with Connection Forgetting from Neural Network DYC Controller[C]. AVEC’02 2001,67(661):2837-2842.

[8] 郭孔辉.汽车操纵动力学[M].长春:吉林科学技术出版社,1991.

[9] Yasui Y, Tozu K, Hattori N, et al. Improvement of Vehicle Directional Stability for Transient Steering Maneuvers Using Active Brake Control[C]. SAE Paper 960485.

[10] Inagaki S, Kshiro I, Yamamoto M. Analysis on Vehicle Stability in Critical Cornering Using Phase-plane Method[C]//International Symposium on Advanced Vehicle Control (1994: Tsukuba-shi, Japan). Proceedings of the International Symposium on Advanced Vehicle Control 1994.

[11] Wu D H, Lin Y H. Directional Response Analysis of Tractor-trailer with Multi-axle-steering Carrying Liquid Load[C]. SAE Paper 2005-01-0415.

[12] 聂晋,周萍.基于PID控制的ABS仿真研究[J].山东交通学院学报,2011,18(4):6-9.