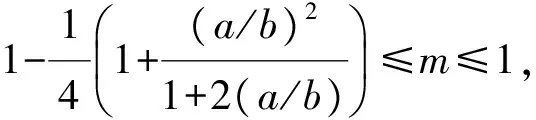截面所受弯矩M为
(5)
截面所能承受的极限弯矩Ms为
(6)
m可表示为
(7)
将式(4)代入式(7)得
(8)
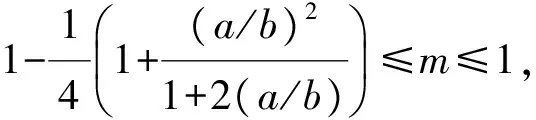
上述推导表明,对于受轴向压力和弯矩组合载荷作用的薄壁梁,当0.67≤m≤1且0≤n≤0.5时,弯矩起主导作用,薄壁梁产生弯曲变形。
1.3 轴向压力起主导作用的情况
当m<0.67且n>0.5时,轴向压力起主导作用,截面的应力分布见图3(b)。此时,压力较大的一侧先屈服,开始产生轴向压溃。而产生塑性变形的截面,其抗弯能力会大大降低。此时如果变形截面受到的弯矩较大,也可能产生弯曲变形;如果弯矩较小,则继续轴向压溃。即在轴向压力起主导作用的情况下,会产生两种可能的结果:轴向压溃、伴随弯曲的压溃,二者之间存在一个产生轴向压溃的临界状态。
截面所受弯矩M可表示为:M=F×e。减小截面所受轴向力F或偏心距e,都可以降低M,从而避免弯曲的产生。F主要来自起主导作用的轴向压溃力,轴向压溃力由薄壁梁的截面设计参数等决定。初始的偏心距则是一个不确定因素。
薄壁梁的轴向压溃力的波形示意图如图5所示,压溃开始时,产生第一个褶皱所需压力值为Fmax,Fmax主要由诱导条件决定。通过诱导设计减小
Fmax,就可以减小F,从而降低截面所受弯矩M。
2 数值模拟
2.1 有限元模型和模拟结果
2.1.1 小尺寸简化模型
为简化运算,先建立尺寸较小的正方形截面薄壁梁模型1和模型2,正方形截面的边长为C,板厚为t,纵长L=160mm。设计参数如表1所示,材料采用理想刚塑性假设,屈服强度为375MPa。边界条件如图6所示,通过施加轴向速度v保证足够大的轴向压力,同时施加横向载荷P实现轴向压力和弯矩的组合载荷状态。诱导方式见图6,在两个相对的平面上凸出d1;在另一对相对的平面上凹入d2。诱导的深度d1和d2决定Fmax的大小,d1或d2越大,Fmax越小。2H为一个压溃褶皱的长度,主要取决于截面边长和板厚。各个方案的模拟结果如图7所示。

表1 小尺寸有限元模型的设计参数和加载条件
2.1.2 实车前纵梁模型
从实车的有限元模型中取前纵梁的前半部分,如图8所示,后端刚性固定,前端受压、弯联合作用,通过改变θ角改变两种载荷的比例。θ=0°时,为仅受轴向压力状态;θ=90°时,为仅受弯矩作用状态。取不同的θ值,其变形如图9所示。注意:当θ=90°时,v的方向为垂直向上。
2.2 结果分析与讨论
2.2.1 轴向压溃的临界状态
(1) 小尺寸简化模型
薄壁梁只受无偏心的轴向压力作用时,可以产生理想的轴向压溃(1-a,2-a)。轴向压力和横向载荷同时作用,横向载荷较小时,虽然有弯曲的倾向,但也可以产生压溃褶皱(1-b,2-b);横向载荷增大到一定程度时,产生了伴随弯曲的压溃(1-c,2-c)。通过将横向弯矩逐步增大的过程,可以发现,1-b,2-b可看作产生轴向压溃的临界状态,1-d,2-d为只受弯矩作用时的弯曲变形。获取方案1-b,2-b和1-d,2-d在距梁底部2H处的截面弯矩-时间曲线,如图10和图11所示。从图10中虚线A、B处获取方案1-b,2-b变形开始时,变形截面所受弯矩M,作为产生轴向压溃的临界弯矩Mc,M=Mc;从图11中虚线A、B处获取截面的极限弯矩Ms。计算m=Mc/Ms,如表2所示,两个模型轴向压溃临界状态时的m都约为0.15。此结果表明:在约为M<0.15Ms的范围内,薄壁梁可以不发生弯曲,产生轴向压溃。

模型12Mc/(N·m)115213Ms/(N·m)7801350m01470158
(2) 前纵梁模型
图9中前纵梁的变形结果表明,其产生轴向压溃的临界状态约在θ为30°~40°之间,根据模拟运算的结果获取各方案的m值,如表3所示。结果表明,该前纵梁模型在压、弯组合载荷作用下,产生轴向压溃的临界条件与上述的小尺寸简化模型基本相同,约为M<0.15Ms。

表3 不同θ值的各方案m值
2.2.2 诱导的作用
方案2-c与2-e的模型尺寸、材料特性和加载条件等完全一致,只有诱导条件不同,通过诱导使方案2-e的Fmax比方案2-c小,轴向压溃力-时间曲线见图12。图13为变形过程中二者的截面弯矩-时间曲线,2-e截面所受的弯矩明显小于2-c,结果2-e产生了轴向压溃而2-c则发生弯曲。此模拟结果验证了前面的理论分析。
3 结论
经过理论分析和数值模拟,可得到以下结论。
(1) 压、弯联合作用的薄壁梁,主要可能产生轴向压溃和弯曲两种变形模式。当M≥0.67Ms且F≤0.5Fs时,弯矩起主导作用,薄壁梁产生弯曲变形;当M<0.67Ms且F>0.5Fs时,轴向压力起主导作用,可能产生两种结果:轴向压溃、伴随弯曲的压溃。
(2) 轴向压力起主导作用时,当M<0.15Ms薄壁梁可以不发生弯曲而产生轴向压溃。
(3) 通过诱导设计减小轴向压溃所需压力,可以降低截面所受弯矩,从而避免弯曲的产生。
(4) 采用的有限元模型较为简化,边界条件等设定较为理想,这导致薄壁梁的刚性比实际偏大,实际碰撞过程中薄壁梁可能更容易弯曲,而压溃条件对应的弯矩会更小。
[1] Abramowicz W. Simplified Crushing Analysis of Thin-walled Columns and Beams[J]. Rozprawy Inzynierskie,1981,29(1):5-26.
[2] Wierzbicki T, Abramowicz W. On the Crushing Mechanics of Thin-walled Structures[J]. Journal of Applied Mechanics,1983,50(4a):727-734.
[3] Abramowicz W, Wierzbicki T. Axial Crushing of Multicorner Sheet Metal Columns[J]. Journal of Applied Mechanics,1989,56(1):113-120.
[4] Abramowicz W, Jones N. Transition from Initial Global Bending to Progressive Buckling of Tubes Loaded Statically and Dynamically[J]. International Journal of Impact engineer,1996,12(5-6):415-436.
[5] Abramowicz W. Thin-walled Structures as Impact Energy Absorbers[J]. Thin-walled Structures,2003,41(2-3):91-107.
[6] Wierzbicki T, Recke L, Abramowicz W, et al. Stress Profiles in Thin-walled Prismatic Columns Subjected to Crush Loading-Ⅱ. Bending[J]. Computers and Structures,1994,51(6):625-641.
[7] Kim H, Wierzbicki T. Numerical and Analytical Study on Deep Biaxial Bending Collapse of Thin-walled Beams[J]. International Journal of Mechanical Sciences,2000,42(10):1947-1970.
[8] Kim H, Raid S. Bending Collapse of Thin-walled Rectangular Section Columns[J]. Computers and Structures,2001,79(20-21):1897-1911.
[9] Kim H, Wierzbicki T. Crush Behavior of Thin-walled Prismatic Columns Under Combined Bending and Compression[J]. Computers and Structures,2001,79(15):1419-1432.
[10] 张金换,杜汇良,马春生,等.汽车碰撞安全性设计[M].北京:清华大学出版社,2010.