缸盖沸腾冷却气泡控制的研究*

张体恩,张卫正,曹元福,2,宋立业

(1.北京理工大学机械与车辆学院，北京 100081； 2.中国北方车辆研究所，北京 100072)

前言

随着内燃机向高功率密度方向发展，发动机冷却能力的提高势在必行。将强制对流欠热沸腾用于发动机冷却系统，可以保证在对发动机冷却水道做细微更改的前提下，大幅度提高换热系数。

将沸腾冷却用于解决缸盖热负荷的过程中，气泡消失是个亟待研究的问题。如果气泡在缸盖中不能迅速地消失，那么它将随流道流向节温器等系统件，对节温器等造成穴蚀。而目前研究对气泡消失行为缺乏清晰的认识。

为避免气泡对系统件的损耗，充分利用沸腾冷却方式，必须研究并分析气泡消失演变规律，对气泡提出有效控制措施。目前针对气泡消失的研究并不多，因为气泡消失并没有作为估计沸腾换热系数的重要参数。当前沸腾气泡演变过程主要基于热扩散方程，然后简化初始与边界条件进行求解[1]。目前关于气泡的诸多研究都是基于热扩散方程来进行能量分析的[2-4]。

文献[5]中基于热扩散控制方程假定，借助能量方程分析气泡演变规律，提出基于热扩散控制方程的气泡消失模型。该模型考虑了包括汽化潜热在内的能量转化过程，针对球形小气泡行为的估计取得了满意的结果。但是由于对能量转化过程考虑不充分，该模型针对大气泡尤其是变形气泡的行为估计结果并不令人满意。

除了能量分析，计算气泡生长与凝结速率目前主要基于归一化关系式[6]。该模型是依据试验数据建立的，其实用价值高，但理论支撑不足。此外，文献[7]中对低压低流速工况下的沸腾气泡行为进行了试验研究,建立了基于试验的无量纲预测模型。

本文中基于试验数据，借助能量方程分析气泡消失行为，考察变形对气泡消失的影响，从而对气泡控制提供指导性建议。

1 气泡消失可视化试验研究

图1为搭建的沸腾换热试验平台的系统示意图。该试验平台由冷却水泵、散热器、带PID温度控制的加热水箱、试验件夹持装置、试验件支撑支架、耐热管道、控制箱、高频电磁感应加热器、进出水温度传感器、进出水压力传感器和流量传感器等组成。

采用外径27mm、壁厚3mm的半环形铸铁铁板为试验件，铁板面上通过人为制造凹坑来形成不同脱离半径的气泡。在铁板外罩以外径32mm、内径28mm的石英管，在石英管外侧利用高频感应加热器对试件进行加热，在试件冷热两侧布置热电偶来测量试件温度和热流密度，试验装置如图2所示。

试验件受热面冷热两侧的温度通过镍铬-镍硅热电偶进行测量，其测量范围为0～1 370℃，测量精度为1℃。通过数据采集仪对试验件进行温度采集，采集频率为10Hz，热流密度采用稳态导热公式计算得到。试验中热流变化如图3所示。由于背侧加热器更靠近测点1，故测点1热流密度最高，而几乎所有的大气泡均在此产生。因此，取测点1为观测点，这里忽略气泡行为对热流密度测量的干扰。

流量通过涡轮流量传感器LWGY25测量，量程为10m3/h，精度为0.01m3/h。在试验段两端安装压力和水温传感器，取两端的测量均值为测试段的水温和压力值。利用高速摄像机拍摄气泡行为，高速摄像机的最高分辨率为1 024×1 024，对应的采样频率为3 600fps，试验采用此采样频率。通过测量气泡上下左右最高点的位置来获取气泡行为信息，每隔0.83ms测量一次。试验工况选择见表1。

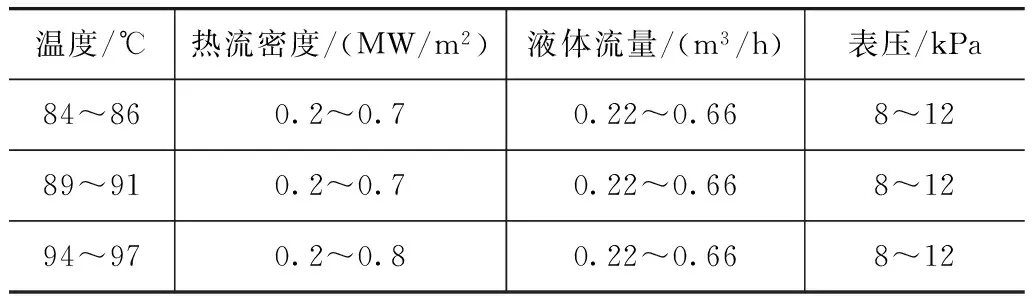
表1 试验工况选择

据试验观察，在低流速高热流密度情况下，气泡脱离和消失状况呈以下特征。

(1) 气泡脱离时局部会依附于加热面，气泡形状不是规则的球形，导致气泡尺寸远大于可估算尺寸。目前常用的气泡脱离尺寸预测模型，如Levy模型[8]、Zeng模型[9-10]预测的气泡脱离直径与本试验观测值并不相符。

(2) 气泡消失是一个失稳的剧烈汽化过程，文献[11]中探讨了变形气泡的失稳过程和作用力。气泡内部压力不稳定，导致在气泡底部形成射流，此外，气泡由于变形会导致换热面积增加。试验中观测到气泡失稳区间为：欠热度(5～14K)。气泡失稳过程如图4所示。

试验中局部流速和温度的变化以及气泡的随机性导致气泡消失行为具有不确定性。因此需要对气泡的极限状况进行评估，从而提出控制气泡的有效措施。本文中假定试验观测的气泡极限尺寸即为该工况下的最大气泡尺寸。文献[12]中的数据表明，相同工况下，气泡脱离直径与平均脱离直径的比值在0.8～1.2之间变动。本试验也观察到，同一工况下气泡尺寸相差并不大。因此，可用观测的最大气泡尺寸代替极限气泡尺寸。

水温为95℃、流量为0.44m3/h和表压为12kPa时的气泡消失状况如图5所示。

2 沸腾气泡消失模型

分析前人研究成果和气泡实验数据，针对缸盖流道特征提出气泡消失假设如下。

(1) 气泡消失时的形状基本为球形，其直径利用气泡长短轴的均值代替。

(2) 气泡内温度不变，近似为饱和液体温度。

(3) 气泡通过液体薄层导热与周围液体进行热交换，气泡散热热量主要来自汽化潜热。

(4) 假定气泡消失过程为气泡生长的逆过程。

(5) 气泡外由过热液体层包围，气泡外液体薄层厚度采用文献[13]中提出的厚度关系式。则气泡消失对应的液体薄层厚度为

(1)

式中：δ为液体薄层厚度；αf为液体热扩散率；tall为消失周期；t为气泡消失时刻。

(6) 假定气泡半径小于30μm时，即认为气泡已经消失。小于30μm的气泡均为球形气泡，由Florschuetz关系式[5]可知，对于起始半径大于3mm的气泡，基于该假设得到的气泡消失时间与理论气泡消失时间误差在2%以内。该假设的提出主要是由于高速摄影在本试验观测角度下的最小观测尺寸为30μm。

大气泡消失作为一种失稳过程，气泡换热面积的增加导致气泡消失速度加剧。通过测量气泡外的凸起点面积得到气泡换热面积，根据试验观测得到：初始气泡半径为R0时，气泡半径在0.9R0～R0区间内气泡换热面积剧烈变化，直到0.9R0达到稳定；在低欠热状态下，气泡尺寸大幅增加和流场温度极度不均是气泡变形的主要原因，因此认为气泡形变因子C主要受流体欠热度和气泡半径R影响，即

C∝(R,(Ts-Tf)-n)

(2)

式中：Ts为液体饱和温度；Tf为流体温度；n为系数。饱和温度与流体温度之差为主流体欠热度ΔTsub。

根据实验数据拟合得到

(3)

式中k为欠热度因子。

根据假设，建立气泡消失模型如下：

(4)

对式(4)进行整理得到

(5)

式中：ρv为饱和蒸汽密度；hfg为汽化潜热；Kf为导热系数；Tb为气泡温度。

3 模型实验验证

气泡消失选取水温为95℃、流量为0.44m3/h和表压为12kPa的工况为验证工况。气泡消失实验与理论对比如图6所示。

利用Florschuetz[5]消失模型预测的气泡消失时间为0.39s，与实验数据相差甚远，主要原因在于大气泡因变形会导致散热面积增大，从而消失速度增加。而本文中模型预测的气泡消失曲线与实验数据符合良好，尤其是气泡消失时间预测与实验符合良好。

不同气泡脱离半径对应不同气泡消失时间。主流体欠热度为7K，流量为0.22～0.66m3/h，气泡消失时间与脱离半径关系如图7所示。

主流体欠热度为12K，流量为0.22～0.66m3/h，对比不同气泡脱离半径的消失时间如图8所示。

气泡消失时间预测与实验数据符合良好，验证了气泡消失模型的合理性。

4 模型误差讨论

(1) 模型忽略了气泡内温度变化，而气泡内实际温度场并不规则，由此导致模型气泡换热计算与实际存在偏差。

(2) 模型中气泡能量仅考虑了起主要作用的汽化潜热能量，忽略了热流体向冷流体传递的能量。

(3) 由于能量方程的简化忽略了对流这一因素，所以模型未考虑流速对气泡消失的影响。实验观察证明，流速仅对气泡脱离半径产生影响，对气泡消失速度的影响可以忽略。

(4) 气泡由于变形导致换热面积增加，是根据实验观察、测量提出的，而其中影响面积增加的因素很多，对换热面积测量的误差是模型误差的主要原因。

(5) 以观测得到的气泡尺寸代替气泡的极限尺寸，势必导致气泡尺寸的估计误差。

5 缸盖气泡消失控制分析

5.1 具体控制要求分析

发动机缸盖水腔鼻梁区具有以下特点：局部区域流道窄，流速慢，热流密度大，产生气泡多等。由此得到缸盖冷却水道气泡控制要求：保证气泡快速消失；保证换热系数保持不变甚至有所提高；保证水流畅通，避免发生气阻。其中保证气泡快速消失是气泡控制的主要难点。由鼻梁区末端到缸盖出口的距离约为50mm，由缸盖出口至节温器的距离约为100mm。为避免节温器受到损耗，需要保证气泡在150mm的距离内快速消失。缸盖内水流速度一般为2.5～3.2m/s[14]，从文献[15]中的实验数据看出，气泡脱离加热面后的移动速度一般为液体流速的0.8～1倍。由此，考虑极限情况，得到气泡的平均移动速度为3m/s，则气泡应保证在0.05s内快速消失。

5.2 气泡消失参数控制

在不改变流道形状的前提下，基于建立的气泡消失模型，对缸盖尤其是鼻梁区沸腾气泡的控制主要由主流体欠热度来控制。

考虑气泡脱离半径的影响。由于气泡的再附着作用，脱离半径难以准确预测，须通过实验进行估计。实验观察发现，当鼻梁区局部流速为0.1～0.3m/s时，气泡最大脱离半径均小于7mm；当流速高于0.3m/s时，气泡最大脱离半径均小于5mm。因此，通过改变流场结构，提高局部流速，能有效降低气泡脱离半径，从而避免大气泡的产生。

两种气泡初始半径，不同欠热度下的气泡消失时间如图9所示。

当局部流速小于0.3m/s时，为使所有气泡在0.05s内快速消失，流体欠热度应大于15K；当局部流速大于0.3m/s时，为使所有气泡在0.05s内快速消失，流体欠热度应大于7K。随着流道流速的增加，欠热度的选择可以相应降低。

现代发动机循环水冷系采用散热器盖，水冷封闭系统内的压力可以提高98kPa以上，而相应的冷却液沸点提高至120℃左右[6]。因此，当受热面局部流速小于0.3m/s时，流体温度设定在105℃以下即可；当局部流速大于0.3m/s时，流体温度可提高至113℃。

5.3 气泡聚合抑制

气泡控制还须考虑气泡聚合问题，避免气泡聚合才能有效避免大气泡的产生。为避免气泡聚合，须在气泡形成过程中使气泡核化点分散化，以降低气泡聚合概率。由核化理论得知，形成气核需要一定的过热度和一定的凹穴半径[1]。

(6)

式中：ΔTsat为液体过热度；Rm为摩尔气体常数；σ为表面张力；M为摩尔质量；ρf为液体密度；rc为空穴半径。

在流速和主流体欠热度不变的前提下，考虑到液体过热度不可更改，根据气核形成条件，应该尽量减小空穴半径rc，即保证水腔表面凹坑尽量小而均匀。因此要求缸盖水腔在铸造过程中应尽量避免砂眼、大凹坑等表面缺陷出现，以抑制气泡聚合。

6 结论

(1) 建立了沸腾气泡可视化试验平台，利用高速摄影对气泡消失行为进行了观测。

(2) 基于能量方程并通过气泡变形分析建立了低欠热下的气泡消失模型。

(3) 缸盖内气泡控制需要保证气泡在0.05s内消失。根据散热器放水压力，流体温度应控制在105℃以下，流体流速提高流体温度也可随之提高。

(4) 为防止气泡聚合，缸盖铸造过程中应防止砂眼等表面缺隐出现。

参考文献

[1] 徐济鋆,等.沸腾传热和气液两相流[M].北京:原子能出版社,2001.

[2] Lind S J, Phillips T N. Spherical Bubble Collapse in Viscoelastic Fluids[J]. Non-Newtonian Fluid Mech,2010,165:56-64.

[3] Brujan E A. Cavitation Bubble Dynamics in Non-Newtonian Fluids[J]. Polym. Eng. Sci,2009,49:419-431.

[4] Wu W, Jones B G, Newell T A. A Statistical Model of Bubble Coalescence and Its Application to Boiling Heat Flux Prediction—Part I: Model Development[J]. ASME J. Heat Transfer,2009,131(121013):1-11.

[5] Florschuetz L W, Chao B T. On the Mechanics of Vapor Bubble Collapse[J]. J. of Heat Transfer, Trans. ASME, Series C,1965,87:209-220.

[6] Akiyama M, Tachibana F. Motion of Vapor Bubbles in Subcooled Heated Channel[J]. Bulletin of J.S.M.E,1974,17(104):241-247.

[7] Prodanovic V, Fraser D, Salcudean M. Bubble Behavior in Subcooled Flow Boiling of Water at Low Pressures and Low Flow Rates[J].International Journal of Multiphase Flow,2002,28:1-19.

[8] Levy S. Forced Convection Subcooled Boiling Prediction of Vapor Volumetric Fraction[J]. Int. J. Heat Mass Transfer,1967,10:951-965.

[9] Thorncroft G E, Klausner J F, Mei R. An Experimental Investigation of Bubble Growth and Detachment in Vertical Upflow and Downflow Boiling[J]. Int. J. Heat Mass Transfer,1998.41:3857-3871.

[10] Zeng L Z, Klausner J F, Bernhard D M, et al. A Unified Model for the Prediction of Bubble Detachment Diameters in Boiling Systems - II. Flow Boiling[J]. Int. J. Heat Mass Transfer,1993,36:2271-2279.

[11] 倪明玖.浮力作用下上升气泡的变形和驻涡形成机理研究[J].工程热物理学报.2009,1(30):76-80.

[12] Rong Situ, Takashi Hibiki, Mamoru Ishii, et al. Bubble Lift-off Size in Forced Convective Subcooled Boiling Flow[J]. Int. J. Heat Mass Transfer,2005,48:5536-5548.

[13] Plesset M S, Zwick S A. The Growth of Vapor Bubbles in Superheated Liquids[J]. J.Appl. Phys.,1954,25:493-500.

[14] 傅松,等.柴油机缸盖水腔流动与沸腾传热的流固耦合数值模拟[J].农业机械学报,2010,4(41):26-30.

[15] Tomio Okawa, Tatsuhiro Ishida, Isao Kataoka, et al. On the Rise Paths of Single Vapor Bubbles After the Departure From Nucleation Sites in Subcooled Upflow Boiling[J]. Int. J. Heat Mass Transfer,2005,48:4446-4459.

[16] 陈家瑞,等.汽车构造:上册[M].5版.北京:人民交通出版社,2007.