CDMA多用户双向中继系统中一种新的功率控制算法

张二伟， 邱 玲

中国科学技术大学个人通信与扩频实验室，合肥230027

随着无线通信系统中数据速率需求的增加，双向中继技术(two-way relaying,TR)作为辅助信息交换技术应运而生.相比于传统中继，双向中继可以将用户之间的信息交换时隙数目从4降至2或3，因而可以成倍提高频谱效率[1].然而在提高频谱的同时，由于时隙数目的减少，用户之间的干扰增加了.

在单用户对场景下，主要应用物理层网络编码(physical-layer network coding,PNC)来解决两个用户之间的自干扰问题，并取得了显著效果[2].但在多用户对场景下，用户对之间的干扰问题涉及到不同的多址方式，比如正交频分多址(orthogonal frequency division multiple access,OFMDA)、码分多址(code division multiple access,CDMA)、时分多址(time division multiple access,TDMA)、空分多址(space division multiple access,SDMA)等.不同的多址接入方式各有优劣：1)SDMA受天线数量的限制；2)OFMDA对相位误差很敏感；3)TDMA所需时隙数较多；4)CDMA自干扰较严重等.目前，这几种接入方式在有关多用户双向中继研究的文献中都有提及[3-6].考虑到OFMDA、TMDA用户对之间没有干扰，已有文献大多研究第2跳的功率分配[3-5]，通过中继功率在不同用户对之间的分配来实现功率效率的优化.然而，采用CDMA接入方式的多用户双向中继系统有干扰受限的特性，造成用户对之间的多用户干扰，于是第1跳的功率控制就成为抑制干扰的关键.

针对上述问题，本文提出了一种CDMA多用户双向中继系统中基于效用函数的功率控制算法，不但可以以较快的速度收敛，而且能够有效降低用户的发射功率.当用户对数目较大时，本文提出的功率控制算法与文献[8]中的算法相比，能够有效降低用户对平均发射功率.

1 系统模型

考虑图1所示的多用户双向中继系统模型，系统中有K个用户对和一个中继节点，bi,j表示用户节点(i∈[1,K]为用户对标号，j∈[1,2]为用户对中用户标号)，R表示中继节点.假设所有用户和中继的工作方式均为半双工且安装1根天线，用户之间没有直接链路，中继端采用MMSE接收机.

图1 系统模型Figur e 1 System model relay to users

多址方式和中继端处理策略参照文献[7]，第1跳的多址方式采用CDMA，且码字之间非正交.中继端采用JD-XOR-F策略进行双向中继的传输处理，则整个传输过程分为两个步骤：

步骤1 所有用户向中继发送数据.假设所有用户均采用二进制相移键控(binary phase shift keying,BPSK)调制，且每个用户对中的两个用户都可以调整自己的发射功率，从而使它们到达中继端的接收功率相同.中继对每一个用户对进行多用户检测，得到每一个用户对中两个用户的叠加符号(-2、0、2)，然后依据文献[7]设计的准则估计两个用户发送符号的异或值.

步骤2 中继得到各个用户对发送符号异或的估计值后，于第2时隙分别在不同的码道上发送.接收端分别在自己分配到的码道上进行接收，只要接收到来自中继端的符号，就能与自己发送的符号进行异或运算得到想要的符号.

(7)第四系。测区第四系广布，约占测区面积的1/3，主要分布于岩溶平原、谷地和柳江两岸。主要发育有河流冲积、溶蚀残余堆积、残坡积、洞穴堆积和风化堆积等五种成因类型。

由于双向中继系统中的性能主要受限于第1跳，故本文研究第1跳中的功率控制算法.在中继端采用MMSE接收机的情况下，中继端的干扰加噪声可以近似为高斯分布[7].第1跳中继接收端接收到用户对i的信干噪比表达式[7]为

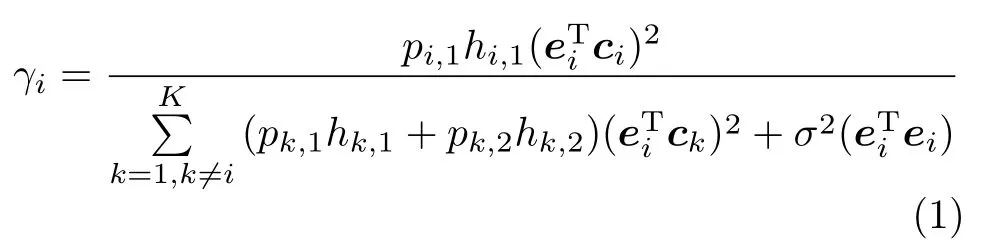
式中，hk,1和hk,2分别表示用户对k中用户1和2与中继之间的信道增益，pk,1和pk,2分别表示用户对k中用户1和2的发射功率，ck表示第k个用户对的扩频码，σ2为中继端的接收噪声，ei为第i个用户对在中继端的MMSE接收向量，具体如下：

2 功控算法设计

针对经典DPC算法的缺陷，文献[10]给出了一种新的基于效用函数的功率控制算法，其最终目标是用户能够以较小的发射功率为代价获得较高的信干噪比.算法的效用函数设计为

式中，b、c均为非负的权重系数，Pr(γi)为用户对i在第1跳的BER，其BER上界为[7]

然而，把式(5)代入到式(4)得到的效用函数在纳什均衡的存在性证明上是无法完成的，于是本文将式(5)进行曲线拟合处理. Pr(γi)为指数曲线，设f(x)=αe-βx.由于拟合函数为非线性函数，需要线性化，故两边取ln得到F(x)=lnα-βx，其中F(x)=ln(f(x)).本文采用文献[11]中的最小二乘法准则进行线性拟合，具体如下：

首先对式(5)取ln，然后等间距取L个点，坐标为(xl,yl),其中l=1,2,···,L，那么拟合后的均方误差为

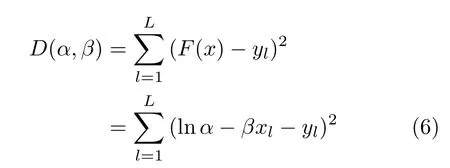
由多元函数的极值原理可知，min{D(α,β)}需满足

求解式(7)可得

再令a=c/α，得到新的效用函数的表达式为

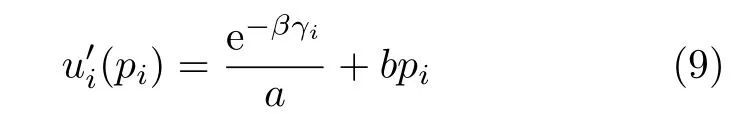
在这个博弈模型中，每个用户对的发射功率最终会达到均衡，即如果将纳什均衡功率表示为p∗，那么系统中某用户对单独改变其发射功率，使其功率偏离这个均衡，于是它的效用将增大，即

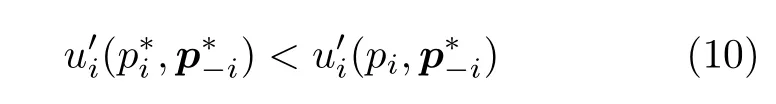
将式(3)代入式(11)，得到用户对i的发射功率表达式

为求解式(12)，本文给出功率控制的迭代算法

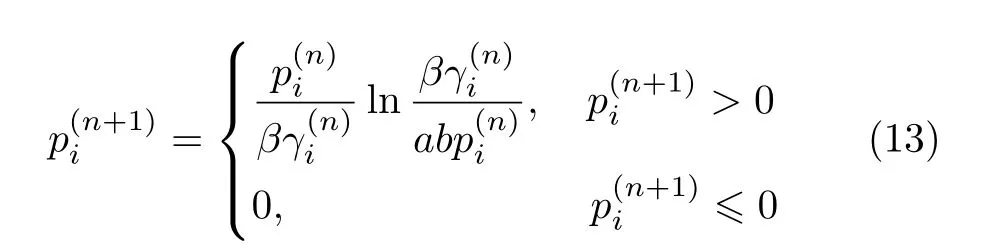
3 纳什均衡的存在性与唯一性

3.1 纳什均衡的存在性证明

根据文献[10]可知：要证明纳什均衡的存在性，只需证明效用函数对总功率的二阶偏导数大于0即可.由式(11)可以得到

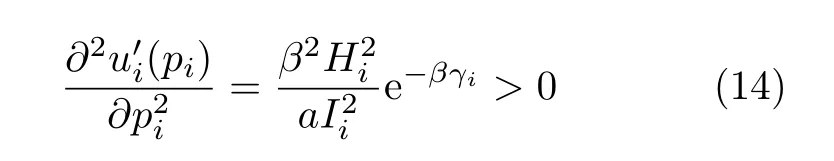
3.2 纳什均衡的唯一性证明

为了证明算法的收敛性，假设函数f(pi)=，则函数f(pi)应该满足以下3条性质[10].

性质1正性f(pi)＞0.

性质2单调性如果p′＞p，那么f(p′)＞f(p).

性质3可扩展性对于任意µ＞1，满足µf(p)＞f(µp).

根据文献[10]给出的求解方法，对满足上述3个性质时需要的条件进行求解可知，若能保证，则性质1～3都可以得到满足.而由式(11)可知，eβγi=，故eβγi＞e，可得信干噪比满足γi＞1/β，即当γi＞1/β时，纳什均衡的唯一性就得到满足.因此，本文将目标信干噪比γtar设置为大于1/β，同时保证系统内所有用户对的信干噪比都大于或等于此目标信干噪比.

4 仿真分析

本节首先验证第2节近似拟合的合理性.取L=10000(保证取样点足够多)，根据式(8)可以计算出α=0.3467，β=0.5610，并得到近似拟合曲线和原曲线的对比图，见图2.可以看出，两条曲线在0～13d B之间几乎重合，平均相对误差为6.77%，说明了本文提出的效用函数能够准确反映真实BER和功率的相互关系，因而是合理的.

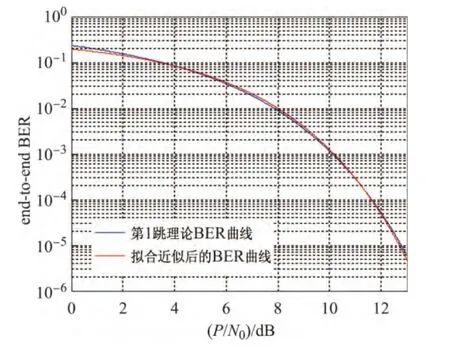
图2 BER函数近似后的拟合度对比图Figur e 2 A comparison of the BER function

其次为了验证本文提出的功控算法的优越性，本节对此算法进行仿真验证.为便于对比，采用文献[10]给出的仿真参数.考虑一个单小区系统，共有30个用户均匀分布在一个2000 m×2000 m的正方形小区内，用户之间随机配对，中继位于小区中心.系统中每个用户对的最大发射总功率都为pmax=0.1W，接收噪声功率σ2=2×10-13mW.信道增益h=A/rµ，其中A=10-11，µ=4.采用256长的扩频序列，同时设置参数a=4,b=0.1，用户对初始发送总功率为2.22×10-16mW，目标SINR设置为γtar=5d B.功控算法的更新表达式[8]为

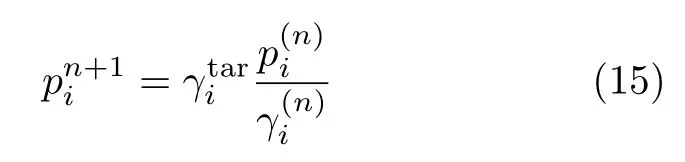
图3比较了本文提出的功控算法和文献[8]提出的功控算法的收敛性.可以看出本文算法具有很好的收敛特性，系统中每个用户对的总发射功率和等效SINR约经10次迭代就可收敛，而文献[8]中的算法需20次选代才能收敛.图4给出了两种功控算法收敛时的SINR，可以看出文献[8]中算法的等效SINR恒定为5dB，这是因为该算法的优化目标就是保证用户对的SINR达到目标SINR；本文给出的功率控制算法的SINR在5d B周围波动，这是因为本文算法以优化功率效率为目标，而没有保证所有条件下达到目标信干噪比的机制.如图5所示，本文算法的收敛功率小于文献[8]中算法的发射功率，达到收敛后UE对的总发射功率为10mW，而文献[8]提出的算法达到收敛后UE对的总发射功率为17mW.可见总功率约减少了40%，而平均信干噪比略有下降.

图3 两种功控算法的收敛速度对比图Figure 3 Comparison of convergence speed of two power control algorithm

图4 两种功控算法达到收敛时的SINRFigure 4 SINR of two power control algorithm transmit when achieve convergence

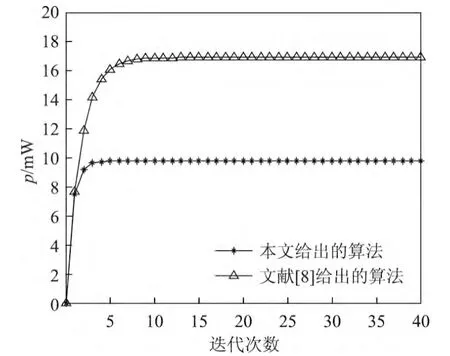
图5 用户对为15时的总发射功率对比图Figure 5 A comparison of total average power when user number is 15

下面比较两种功率控制算法下的发射功率，其中用户对与中继之间的等效距离定义为

图6给出了用户对与中继等效距离和发射功率的关系，可以看出对于与中继等效距离较小的用户对来说，采用本文算法比采用文献[8]中的算法得到的发射功率大；反之，采用本文算法得到的发射功率显著下降.这是因为本文算法在效用函数中引入了功率惩罚因子，惩罚了距离中继较远的用户对，减小了发射功率，但SINR得不到保证.而对于距离中继较近的用户对来说，相同的发射功率可以获得更高的SINR，故采用本文算法会减小发射功率.

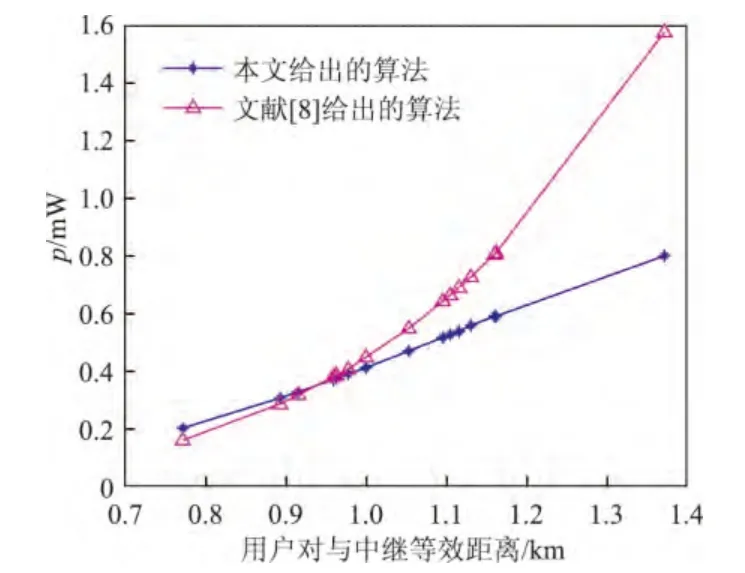
图6 两种功控算法达到收敛的发射功率与等效距离Figure 6 Relationship between transmit power and equivalent distance when achieve convergence

最后比较两种算法在用户对数目增加的情况下，达到收敛的用户对平均发射功率的大小，如图7所示.当用户对数目为8时，两种算法平均发射功率的差距基本为0，但当用户对数目为15时，文献[8]中的算法所对应的平均发射功率是本文算法的1.69倍，两者之间的差距随用户对数目的增加而增大.这是因为随着用户对数目的增加，系统中干扰加大.文献[8]提出的算法不计代价地保证满足目标SINR，需要消耗较多的功率；本文算法把功率用到效用最高的用户对上，但在一定程度上牺牲了部分边缘用户对的SINR性能.

5 结语

在多用户对双向中继系统中，用户对之间的干扰直接影响整个系统的性能，而抑制用户对之间干扰的有效手段之一就是功率控制.为此，文献[8]提出了一种多用户CDMA双向中继系统中的功控算法，实质上就是经典的DPC算法，但其收敛速度慢，达到收敛时的功率较大.本文针对上述问题，提出了一种新的基于效用函数的功控算法，根据第1跳BER的近似拟合设计新的效用函数.与文献[8]提出的算法相比，本文算法收敛速度快，达到收敛的功率小，且更适用于用户对数目较多的场景，因此具有更广阔的应用前景.

图7 用户对总平均发射功率与用户对数的关系Figure 7 Relationship total average transmit power and user number

[1]YANG H J,LEE K C,CHUN J H.Zero-forcing based two-phase relaying[C]//IEEE International Conference on Communications,2007:5224-5228.

[2]POPOVSKI P,YOMO H.Physical network coding in two-way wireless relay channels[C]//IEEE International Conference on Communications,2007:707-712.

[3]XU H W,ZOU J N.Auction-based power allocation for multiuser two-way relaying networks with network coding[C]//Global Telecommunications Conference(GLOBECOM 2011),2011:1-6.

[4]SHIN W J,LEE N Y,LIM J B,SHIN C Y.Power allocation for two-way relay system based on sequential seconf price auction[C]//2011 Third International Conference on Ubiquitous and Future Networks(ICUFN),2011:146-151.

[5]CHEN M,YENER A.Power allocation for F/TDMA multiuser two-way relay networks[J].IEEE Transactions on Wireless Communications,2010,9:546-551.

[6]CHENM,YENERA.Multiuser two-way relaying:detection and interference management strategies[J].IEEE Transactions on Wireless Communications,2009,8(8):4296-4305.

[7]CHEN M,YENER A.Multiuser two-way relaying for interference limited systems[C]//IEEE International Conference on Communications,2008:3883-3887.

[8]CHEN M,YENER A.Interference management for multiuser two-way relaying[C]//Information Sciences and Systems,2008:246-251.

[9]ZANDER J.Performance of optimum transmitter power control in cellular radio systems[J].IEEE Transaction on Vehicular Technology,1992,41(1):57-62.

[10]喻的雄，蔡跃明，钟卫.CDMA系统中一种新的分布式博弈功率控制算法[J].电子与信息学报，2008，30(2):443-446.YUDixiong,CAIYueming,ZHONGWei.A novel distributed power control algorithm in CDMA system:a game theoretic approach[J].Journal of Electronics&Information Technology,2008,30(2):443-446.(in chinese)

[11]石振东，刘国庆.实验数据处理与曲线拟合技术[M].哈尔滨：哈尔滨船舶工程学院出版社，1991:184-189.