一类线性切换系统的观测器设计

杨 寅， 孙文安， 裴炳南

大连大学信息工程学院，辽宁大连116622

切换系统是一类较为重要的混合系统,它由多个子系统及其切换规则构成[1-3].切换系统的控制器的设计大多基于状态反馈，但在实际系统中的状态往往不可直接观测，于是本文尝试设计相应的状态观测器来解决该问题.

由于切换系统本身的复杂性，对其观测器的设计也相对复杂.现有的研究成果大致分为两类，一类是已知切换系统的切换规则，另一类是未知切换系统的切换规则.对于切换规则和观测状态都需要估计的观测系统，研究成果还不多见.文献[2]提出的模型包括连续观测器和定位观测器两部分，前者可以估计切换系统的连续部分，即系统状态；后者可以估计切换系统的离散动态事件，即切换规则，如图1所示.

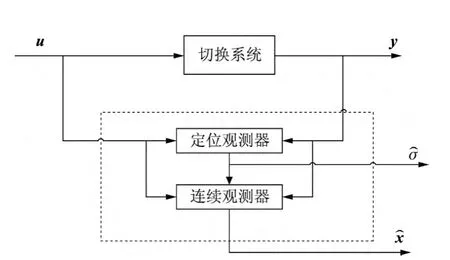
图1 观测器模型Figure 1 Model of the observer

在文献[2]的基础上，文献[4]针对一类非线性切换系统设计了相应的模型预测控制器，并给出了该系统闭环状态一致有界的充分条件；文献[5-6]则利用有限状态机(f inite state machine,FSM)设计了一类定位观测器，可以由已知的参数在一定时间内识别出切换系统的切换规则，同时借助于共同Lyapunov函数法研究了一类具有切换延迟的观测器，给出了该系统的估计误差是稳定的结论.文献[7]将切换延迟和L2增益分析相结合，根据平均驻留时间方法研究了一类具有切换时延的切换系统的稳定性，同时也给出了相应的L2性能.文献[8]考虑了一类线性离散切换系统的滤波器设计问题，在候选子滤波器和对应的子系统之间存在异步行为的条件下，利用平均驻留时间方法研究了相应的切换律和稳定的充分条件，并给出了系统的H∞性能.文献[9]研究了一类存在不可观测子系统的非线性切换系统，采用平均驻留时间法设计观测器，随后根据多Lyapunov函数法证明了该系统的稳定性.

本文同样基于文献[2]，重点研究连续观测器部分的设计，不考虑定位观测器的设计即假设已经设计好了定位观测器，它总是能在某一段时间内正确地跟踪到切换系统当前的切换规则.同时本文假设切换系统经过有限次切换后渐近稳定以及定位观测器的跟踪时间小于被观测系统的切换时间，利用共同Lyapunov函数法得到了观测系统的状态估计误差指数衰减的结论.最后类似于卡尔曼对观测器的改进[10]，利用基于超平面概念的投影法对状态进行修正，进一步加快了估计误差的收敛速度.

1 系统的描述与准备

如图1所示的线性切换系统[2]，其连续部分数学模型可以描述为

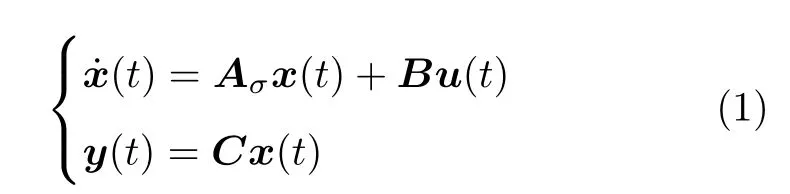
式中，x(t)∈Rn为系统的状态向量，u(t)∈Rp为控制输入，y(t)∈Rq为量测输出，Ai∈Rn×n,B∈Rn×p,C∈Rq×n为常值矩阵.σ:[0,+∞)→M={1,2,···,m}是系统的切换信号，决定了在某一确定时刻ti时系统i的启动依赖于时间t的分段常值函数.定义切换系统的切换时间集合如下：

对于系统(1)，定义连续输出观测器系统

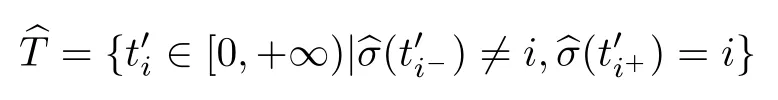
本文研究的切换系统在有限时间内切换有限次，且满足以下4条假设：

假设1 系统(1)存在某一切换律σ(t)，使得作用在该切换律下的系统(1)的状态经过有限次切换后渐近趋向于0.

假设3 矩阵对(Ai,C)是可观测的.

假设4 定义观测误差为~x=x-^x，系统的观测误差状态~x存在某一边界值

式中，ε＞0.同时存在某一时刻τ0＞0以及某一常数xmax＞0，使得

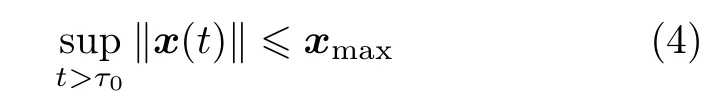
误差系统的动力学描述为

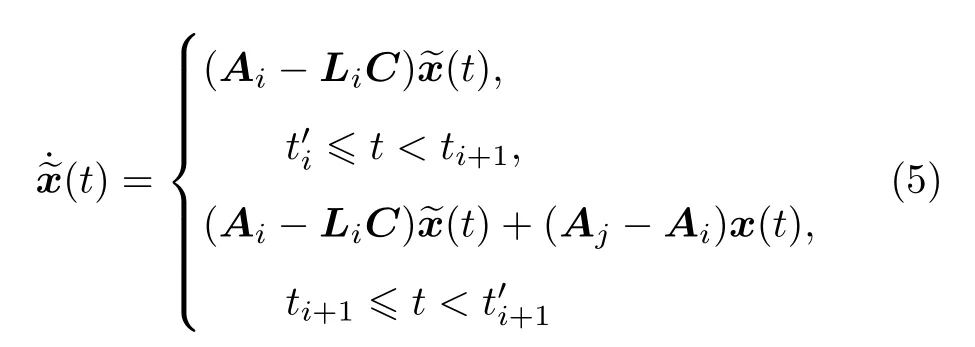
式中，ti+1表示切换时刻ti的下一次切换时刻，j∈σ(t),i∈.显然，当系统(2)还未辨认出系统(1)的运行模式即t∈时，i/=j；随后经过时间fi，i=j，如图2所示.

图2 两种切换时间的示意图Figure 2 Illustrate of two kinds of switching time

定义1[5]如果存在正定矩阵P，常数θ＞0及分段常值的切换函数，使得正定函数V(~x)=沿系统(5)轨线的导数满足

引理1[11]设Y、M、N为具有适当维数的矩阵，其中Y是对称矩阵，则对任意满足ΓTΓ≤I的矩阵Γ，有

当且仅当存在常数λ＞0，使得

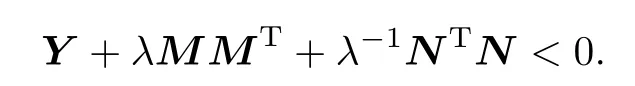
2 主要结果

为了书写简洁，在下列矩阵中均以符号“*”表示矩阵的对称结构.

2.1 线性切换系统的观测器设计

定理1 若系统(1)满足假设1～4，并且存在矩阵Di∈Rn×q，实正定对称阵P∈Rn×n，以及常数ε、γ、α、β、λi均大于0，使得下列矩阵不等式可解，则误差系统(5)是指数稳定的.这里选取观测增益矩阵为Li=P-1Di.

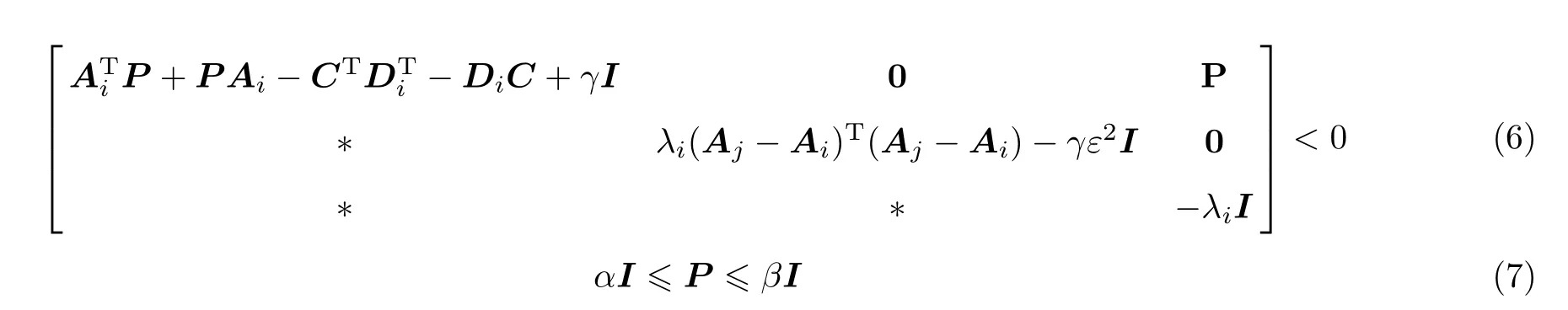
证明 对于误差系统(5)，构造Lyapunov函数V(t)=,t∈，则Lyapunov函数沿着系统(5)的导数为

1)当t∈[ti+1,)时，i/=j，

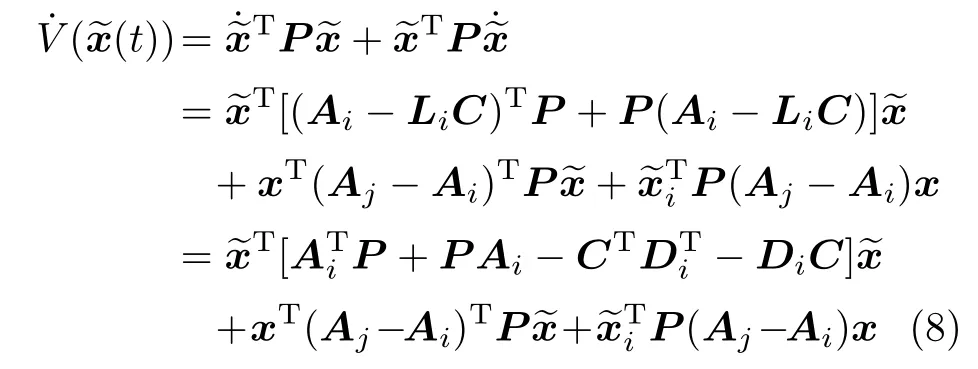
根据引理1可得

将其代入式(8)得

总之，在布雷顿森林协议基础上建立的现行的国际经济秩序，尽管在制度设计上存在着自由主义因素，这些因素包括自由平衡贸易的思想、古典经济学货币数量论以及保留了大危机之前建立的主张金融自由的跨国金融组织，但是总体而言，它的运行主要是为给西方国家的国内政府干预政策提供良好的外部环境。因此，它的政策选择次序是先国内、后国际，先贸易、后金融。这一制度特征在1945～1958年间没有发生本质性的变化。

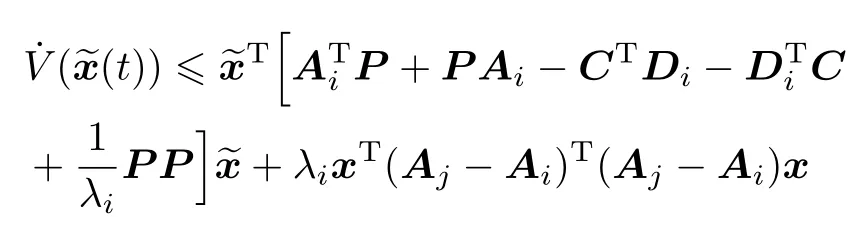
将上式化为二次型的形式

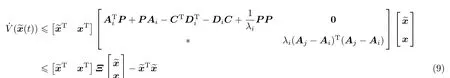
式中

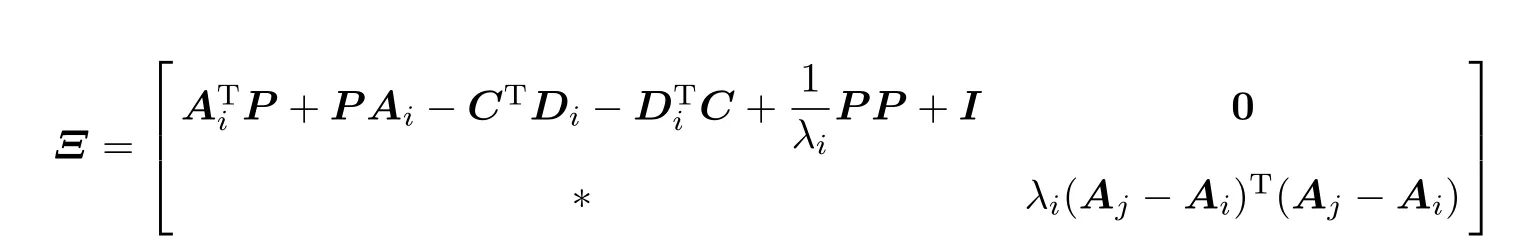
下面将式(3)变换为二次型形式

改写成

式中

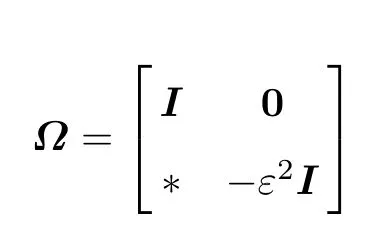
根据Schur补引理可知条件(6)等价于

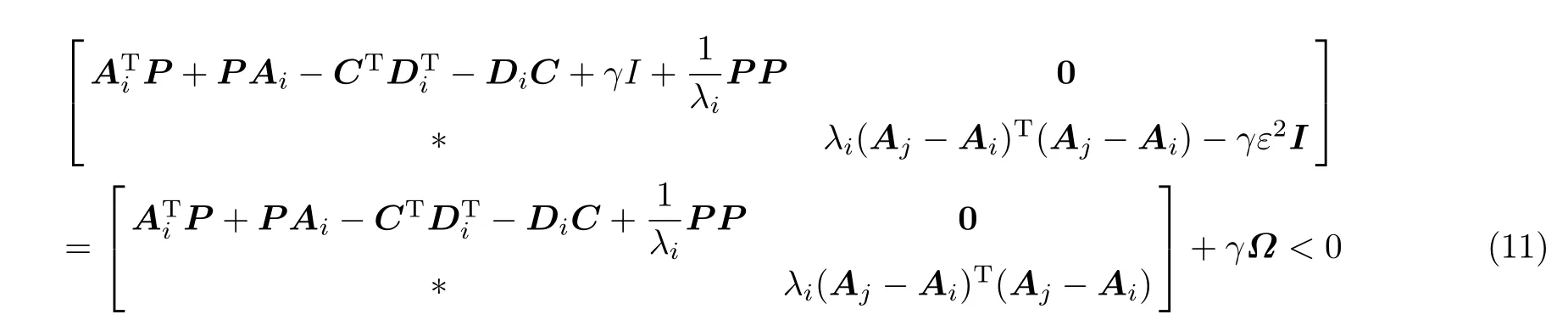
将式(9)进行恒等变换，并结合式(10)和(11)可得

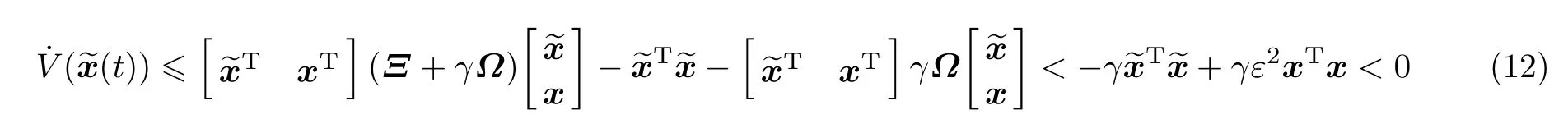
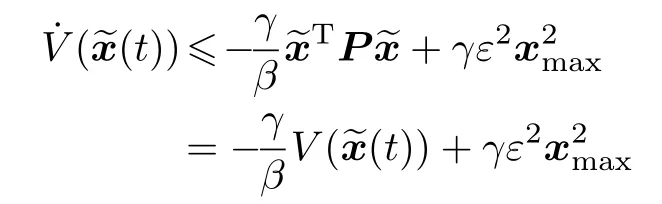
解得

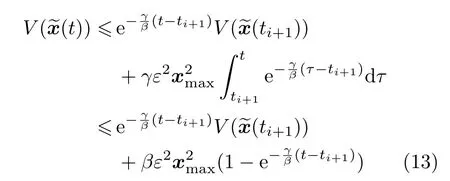
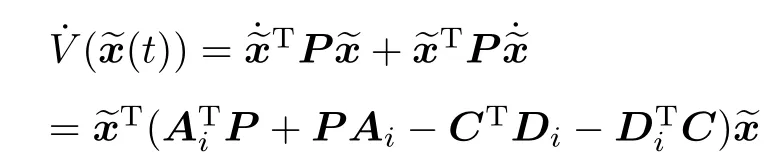
类似于上面的证明，并利用(6)中的条件(Ai-LiC)TP+P(Ai-LiC)+γI＜0，可以得到如下不等式：

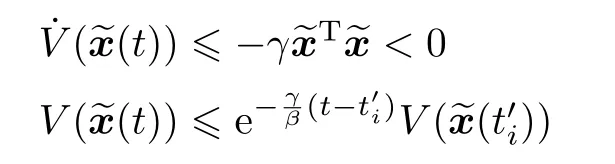
由假设1可知系统(1)经过i+1次切换后渐近稳定，即不再切换了，此时观测系统(2)的切换律在跟踪上系统(1)后不再改变.当t→∞时，有

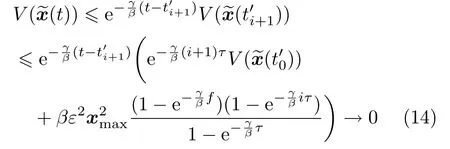
根据定义1取θ=γ，则此时的误差系统(5)指数收敛，定理1得证.

注1 当切换系统的运行时间为无穷时，式(14)的后一项不会趋向于零，则误差系统的能量函数存在某一上界.此时尽管存在观测误差，但通过设计合适的γ、β、ε等参数，可以获得满意的误差范围.

2.2 线性切换系统的观测器优化设计

接下来，通过加入状态跳变来改进观测系统的估计误差收敛速度.

定理2 若每次在系统(1)的切换时刻ti上，观测器状态存在跳变

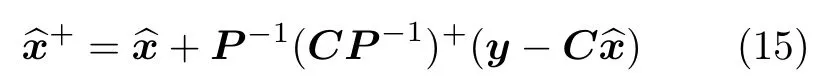
式中，(∗)+表示矩阵∗的广义逆矩阵.

证明 由上述讨论可知P是实正定矩阵，故对其求逆矩阵是成立的.同时由定理2中的条件知y=Cx=，状态x和处于同一超平面上，如图3所示.

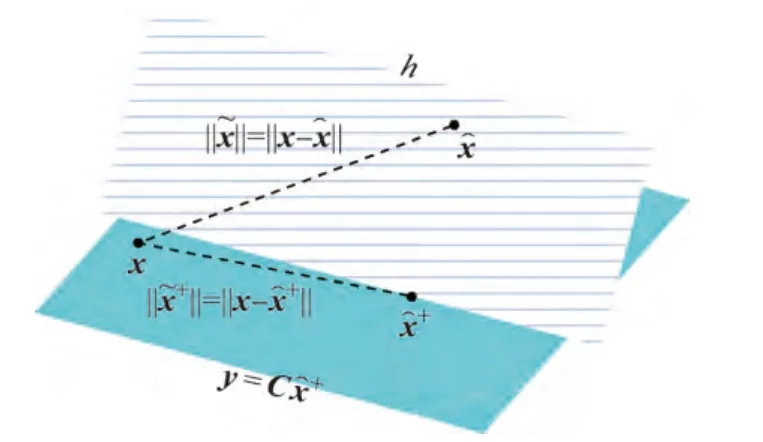
图3 状态^x投影到超平面y=上的示意图Figure 3 Projection of^x onto the plane y=

从图3中可以看出，当^x+和^x处于同一个正交于y=C^x+的超平面h上时，利用勾股定理可以得到

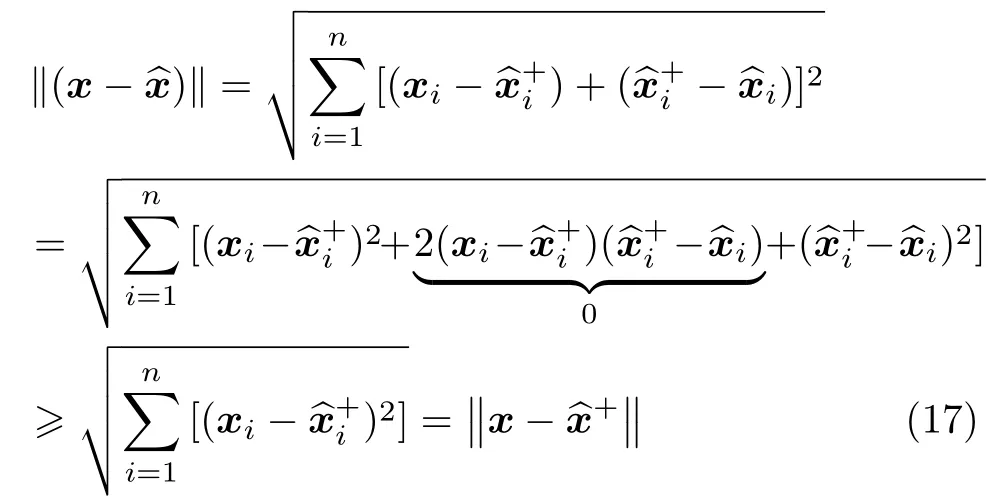
式中，广义逆矩阵(CP-1)+的存在性由假设3即矩阵C∈Rq×n是行满秩这一条件保证，由此证明完成.

注2 在观测器中加入状态跳变后，在每次的切换时刻估计误差的值总小于原先未加入跳变时的值，于是加快了估计误差的衰减速度，使误差系统(5)更快地收敛到平衡点，从而改善了观测器的性能.

3 仿真算例

以两个子系统综合仿真上面所提出的结论，定义系统(1)模型如下：

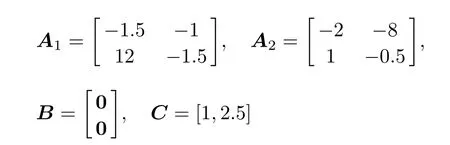
定义系统(1)的切换面为

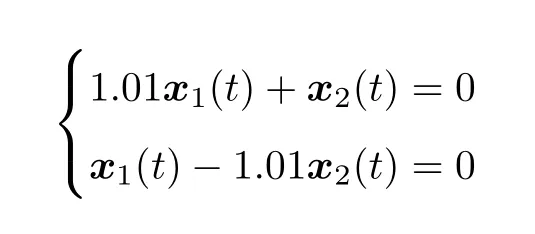
选择α=1，ε=3.67，λ1=1.3，λ2=0.5，由定理1解LMI得，同时得到β =46.16，γ=12.83.仿真结果如图4和5所示，其中系统的初始状态为x(0)=[10,6]T，观测器的初始状态为^x(0)=[12,7.5]T.

图4 未改进的观测系统(2)与切换系统(1)的状态轨迹线Figur e 4 State trajectories of system(2)and(1)without using projection

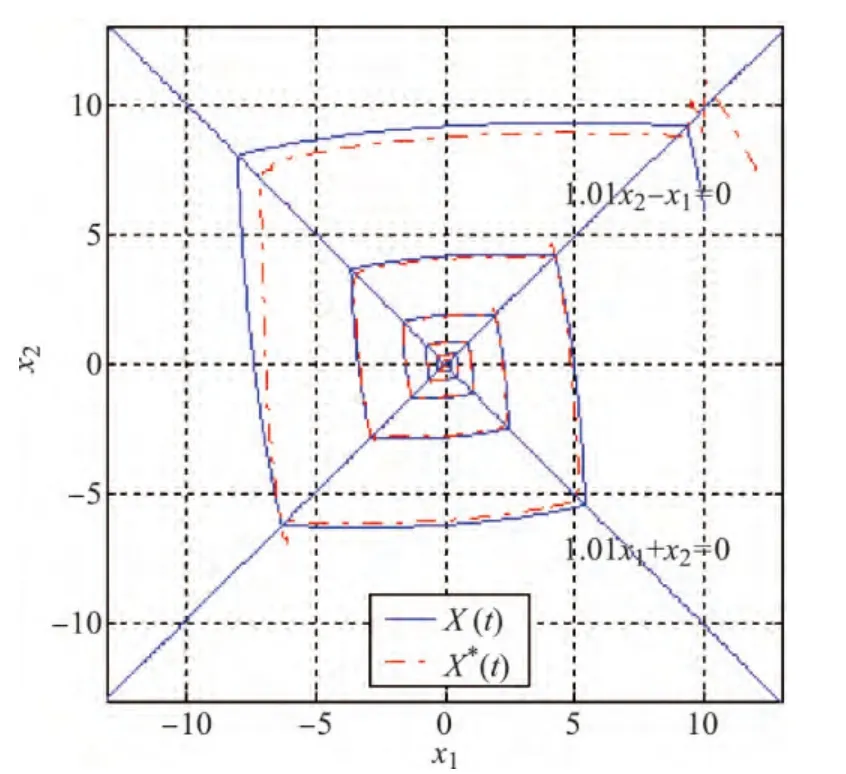
图5 改进后的观测系统(2)和切换系统(1)的状态轨迹线Figur e 5 State trajectories of system(2)and(1)using projection

图6切换系统(1)和观测系统(2)的切换信号Figure 6 Switching signal of the system(1)and(2)

图4 ～6中的X(t)、X′(t)分别表示切换系统的状态x(t)=[x1,x2]T及观测系统的状态由图4可以看出，跟踪状态和原状态之间的误差越来越小，且由假设1知这两种状态都收敛至平衡点.图5中状态之间的误差明显小于图4，这与定理2所证结果一致.

4 结语

本文考虑了一类未知切换规则的线性切换系统状态观测器的设计问题，利用共同Lyapunov函数法给出了观测器误差系统指数稳定的充分条件，并通过仿真实例验证了本文结论的有效性，从而为切换系统的状态观测器的设计提供了一种有效的方法.

[1]XIEG,WANGL.Stabilization of switched linear systems with time-delay in detection of switching signal[J].Journal of Mathematical Analysis and Applications,2005,305(1):277-290.

[2]PETTERSSON S.Switched state jump observers for switched systems[C]//Proceedings of the 16th IFAC Word Congress,2005,Prague.Tu—E12—TO/5.

[3]ZHANG Lixian, GAO Huijun.Asynchronously switched control of switched linear systems with average dwell time[J].Automatica,2010,46(5):953-958.

[4]LIU Jinfeng,MUÑOZD,PEÑAB D L,CHRISTOFIDES P D.Distributed model predictive control of nonlinear systems subject to asynchronousnext term and delayed measurements[J].Automatica,2010,46(1):52-61.

[5]PETTERSSON S.Observer design for switched systems using multiple quadratic Lyapunov functions[C]//2nd IFAC Conference:Analysis and Design of Hybrid Systems,2006,Alghero:18-23.

[6]De SANTIS E,DI BENEDETTO M D.Observer design for discrete-time linear switching systems[C]//Proceedings IFAC Workshop on Dependable Control of Discrete Systems,2007,ENS Cachan,France:311-316.

[7]XIE D,WANG Q,WU Y.Average dwell-time approach to L2gain control synthesis of switched linear systems with time delay in detection of switching signal[J].Control Theory&Applications,2009,3(6):763-771.

[8]ZHANG Lixian,CUI Naigang,LIU Ming,ZHAO Ye.Asynchronous f iltering of discrete-time switched linear systems with average dwell time[J].IEEE Transactions on Circuits and Systems,2011,58(5):1109-1118.

[9]向峥嵘，向伟铭.一类非线性切换系统观测器设计的新方法[J].系统工程与电子技术，2009,31(2):416-419.

XIANGZhengrong,XIANGWeiming.A new approach to observer design for a class of switched nonlinear systems[J].Systems Engineering and Electronics,2009,31(2):416-419.(in Chinese)

[10]KALMANR E.A new approach to linear f iltering and prediction problems[J].ASME Journal of Basic Engineering,1960,82(4):35-45.

[11]顾则全，刘贺平，廖福成，王允建.基于LMI的不确定时滞切换广义系统的保成本控制[J].系统工程与电子技术，2010,32(1):147-151.

GUZequan,LIUHeping,LIAOFucheng,WANGYunjian.Guaranteed cost control for uncertain timedelay switched singular systems based on LMI[J].Systems Engineering and Electronics,2010,32(1):147-151.(in Chinese)