刚度对转子系统随机响应的影响＊

王正浩， 席庆泰， 熊兴荣， 孟庆欣， 杨兴涛

（沈阳建筑大学交通与机械工程学院 沈阳，110168）

引 言

随着旋转机械向着高性能、高效率方向发展，近年来国内外学者针对旋转机械从不同角度开展了广泛研究［1-9］。在抗震设计中，研究发电机转子等在地震激励下的振动特性是一个非常重要的问题，对复杂转子系统进行随机响应分析是系统安全可靠运行的重要保证，但由于问题的困难和复杂性，这方面的研究较少，数值计算也不多见［10-11］。转子系统随机响应分析的方法有蒙特卡罗法和功率谱算法等，但由于其计算过程过于复杂，计算量非常大，往往使工程人员望而却步。林家浩等提出的虚拟激励法是对线性随机振动系统进行谱分析的有效工具［12］，该方法将平稳随机激励转化为稳态简谐激励，将非平稳随机激励转化为瞬态确定性激励，具有简单、高效、精确等优点。考虑到现代机械的高速、高精度化，笔者针对计及机匣弹性、陀螺力矩并同时考虑机匣与定子间的弹性联接的悬臂双盘转子系统，应用虚拟激励法，分析了系统在轴承回转随机动力激励、转子不平衡随机激励和地面平稳随机地震激励下的随机响应，并讨论了系统刚度变化对随机响应的影响，为转子系统工作参数的合理选择和随机振动控制提供依据。

1 轴承回转随机动力激励

在航空燃气涡轮发动机等旋转机械中，由于制造误差等原因，滚动球轴承的内外圈与滚动体之间实际上存在有微小间隙。如果滚动体直径不相同，则在大的滚动体插入方向上，如图1所示，径向间隙变小，刚度增大Δk，而在其垂直方向上径向间隙变大，刚度减小Δk，即在相互垂直的方向上存在轴承刚度差。这种轴承刚度差随转动坐标系Ox′y′按滚动体的公转角速度ω′旋转，激发转子系统振动。在y′和x′方向上轴承的弹性恢复力大小分别为

图1 轴承刚度差Fig.1 Model of the bearings stiffness difference

根据坐标变换，得到

其中：φ为在［0～2π］上均匀分布的随机变量。

在y和x方向上的弹性恢复力大小分别为

将式（2）代入式（3）得

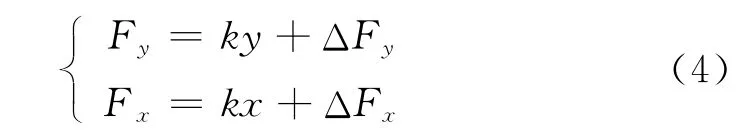
其中：ΔFy和ΔFx分别为由于轴承回转随机动力激励引起的y和x方向上弹性恢复力大小的改变量。

转动坐标系Ox′y′旋转角速度ω′＝αω，其中：α＝D／［2（D＋d）］，D和d分别为轴承内圈直径和滚动体直径；ω为轴旋转角速度。轴承刚度差Δk＝εk，其中：ε为轴承回转随机动力激励参数；k为轴承刚度。

2 系统力学模型与随机运动微分方程

转子系统力学模型如图2所示。设机匣为具有线性径向接触刚度的弹性圆环，在随机激振力作用下，系统随机运动微分方程为

图2 转子系统力学模型Fig.2 Model of rotor system

位移列阵、随机激振力列阵、质量矩阵、陀螺矩阵、阻尼矩阵和刚度矩阵分别为

其中：

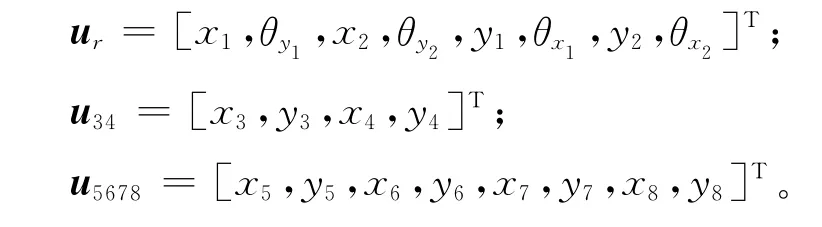
随机激振力列阵F＝F1＋F2，其中随机激振力列阵F1中的元素包括重力、转子不平衡随机激振力和轴承回转随机动力激励，随机激振力列阵F2为地面随机地震激励，F1和F2分别为

φ，φ1，φ2为在［0～2π］上均匀分布的随机变量。

分析表明，水平方向地震时转子系统的随机响应相对比较强烈，故取惯性力指示向量为

其中：

其中：

其中：

C123456为8行8列对称矩阵，主对角线上的元素为

第1行第5列元素为－C3x，第2行第6列元素为－C3y，第3行第7列元素为－C4x，第4行第8列元素为－C4y，其余元素为零。

其中：Kr1和Kr2由转子柔度矩阵确定；K1和K2为交叉刚 度 矩 阵；K3＝diag（k3x，k3y，k4x，k4y）；K4＝diag（k3x＋k5x＋kj1x，k3y＋k5y＋kj1y，k4x＋k6x＋kj2x＋kj3x，k4y＋k6y＋kj2y＋kj3y）；K5＝diag（k7x＋kj3x，k7y＋kj3y，k8x＋kj1x＋kj2x，k8y＋kj1y＋kj2y）。

3 系统随机响应的虚拟激励分析

按虚拟激励法的基本原理［11-12］，应构造虚拟激励，由系统随机运动微分方程式（6），得到系统虚拟振动微分方程

求解虚拟振动微分方程式（8），可得虚拟响应为

其中：

进而可得到位移随机响应的功率谱矩阵

其中：上标“＊”代表取复共轭。

4 系统随机响应数值计算

在随机响应数值计算中采用的计算数值为：轴材料密度ρ＝7.8×103kg／m3；弹性模量E＝210×109N／m2；三段轴直径均为di＝30mm（i＝1，2，3）；三段轴截面惯性矩Ii＝π／64（i＝1，2，3）；三段轴长度分别为l1＝210mm，l2＝330mm和l3＝240 mm；轴颈质量m3＝3kg，m4＝3kg；圆盘质量mii＝24.335 3kg（i＝1，2）；圆盘等效质量分别为m1＝25.900 9kg，m2＝24.725 1kg；半径Ri＝120mm（i＝1，2）；厚度Bi＝69mm（i＝1，2）；极转动惯量JPi＝mii／2（i＝1，2）；直径转动惯量Jdi＝Jpi／2；机匣质量mi＝2m1（i＝5，6，7，8）；滚动轴承阻尼Cix＝Ciy＝0（i＝3，4）；滚动轴承为深沟球轴承6304，α＝0.36；机匣阻尼Cix＝Ciy＝20Ns／m（i＝5，6，7，8）；材料内阻尼Cc＝20Ns／m，外阻尼Cei＝Ce＝350Ns／m（i＝1，2）；地震方向为水平方向；平稳白噪声地震激励谱密度SO＝1.35×10－1m2／s3；圆盘偏心矩e1＝e2＝e＝0.02mm；轴承回转随机动力激励参数ε＝0.006；转速n＝8kr／min。

4.1 机匣刚度kjx对随机响应的影响

取机匣之间的弹性联接刚度kjix＝kjiy＝kj（i＝1，2，3）＝107N／m，滚动轴承刚度kix＝kiy＝k（i＝3，4）＝6×107N／m。图3为机匣刚度分别为kix＝kiy＝kjx（i＝5，6，7，8）＝107N／m（曲线1），kjx＝108N／m（曲线2），kjx＝109N／m（曲线3）和kjx＝2×109N／m（曲线4）时圆盘和轴承的随机响应功率谱密度。由图3可知：机匣刚度对随机响应的影响较大，特别是对轴承的随机响应影响更大；当机匣刚度大于108N／m以后，机匣刚度对随机响应的影响基本稳定；机匣刚度的选取原则上应该大于108N／m。

4.2 机匣联接刚度kj对随机响应的影响

取机匣刚度为kix＝kiy＝kjx（i＝5，6，7，8）＝108N／m，滚动轴承刚度kix＝kiy＝k（i＝3，4）＝6×107N／m。图4为机匣联接刚度分别为kjix＝kjiy＝kj（i＝1，2，3）＝0（曲线1），kj＝106N／m（曲线2），kj＝108N／m（曲线3）和kj＝1010N／m（曲线4）时圆盘和轴承的随机响应功率谱密度。由图4可知：机匣联接刚度对轴承随机响应的影响明显，而对圆盘随机响应的影响不大；机匣联接刚度大于108N／m比较合适。

4.3 轴承刚度k对随机响应的影响

取机匣刚度为kix＝kiy＝kjx（i＝5，6，7，8）＝108N／m，机匣联接刚度为kjix＝kjiy＝kj（i＝1，2，3）＝107N／m。图5为轴承刚度分别为k＝1.5×107N／m（曲线1），k＝2×107N／m（曲线2），k＝1 0×107N／m（曲线3）时圆盘和轴承的随机响应功率谱密度。由图5可知：轴承刚度越小，随机响应（特别是低频随机响应）越强烈；轴承刚度取值大于2×107N／m为宜。

图3 机匣刚度对随机响应的影响Fig.3 The influence of casing stiffness on random responses

图4 机匣联接刚度对随机响应的影响Fig.4 The influence of casing connection stiffness on random responses

图5 轴承刚度对随机响应的影响Fig.5 The influence of bearing stiffness on random responses

5 结束语

应用虚拟激励法，分析复杂转子系统在多参数耦合随机激励－轴承回转随机动力激励、转子不平衡随机激励和地面平稳随机地震激励作用下的随机响应是适宜的。通过数值模拟得到的主要结论是：机匣刚度、机匣联接刚度和轴承刚度的变化对随机响应都有较大影响；比较合适的系统刚度数值为机匣刚度和机匣联接刚度应大于108N／m，轴承刚度应大于2×107N／m。

［1］ 闻邦椿，武新华，丁千，等.故障旋转机械非线性动力学的理论与试验［M］.北京：科学出版社，2004：2－4.

［2］ Yanbe S.Rotor vibration due to collision with annular guard during passage through critical speed［J］.ASME Journal of Vibration and Acoustics，1998，120：544－550.

［3］ Yuan Huiqun，Li He，Wen Bangchun.Study on stability and bifurcation behavior of the rotor with local rubbing［C］∥Proceedings of the First International Conference on the Integration of Dynamics，Monitoring and Control.Manchester：［s.n.］，1999：305－308.

［4］ Wen Bangchun，Li Z P，Yao Hongliang，et al.Dynamics of rotor－bearing system with coupling faults of pedestal looseness and rub－impact［C］∥Proceedings of the 11th World Congress on Theory of Machine and Mechanism.Tianjin：［s.n.］，2004：156－165.

［5］ Sankaravelu A，Noah S T，Burger C P.Bifurcation and chaos in ball bearings［J］.Nonlinear and Stochastic Dynamics，1994，192（78）：313－325.

［6］ Wang Y.Prediction of periodic response of rotor dynamics stems with nonlinear supports［J］.ASME Journal of Vibration and Acoustics，1997，119：346－353.

［7］ Zhang Yimin，Wen Bangchun.Reliability sensitivity for rotor－stator systems with rubbing［J］.Journal of Sound and Vibration，2003，259（5）：1095－1107.

［8］ 刘长利，谢朋儒.基于有限元的呼吸裂纹转子动力学特性［J］.振动、测试与诊断，2011，31（2）：185－190.

Liu Changli，Xie Pengru.Dynamics characteristics of rotor with breathing crack using finite element method［J］.Journal of Vibration，Measurement ＆Diagnosis，2011，31（2）：185－190.（in Chinese）

［9］ 张义民，何永慧，朱丽莎，等.多平行轴齿轮耦合转子系统的振动响应［J］.振动、测试与诊断，2012，32（4）：527－531.

Zhang Yimin，He Yonghui，Zhu Lisha，et al.Vibration response of multi－shaft rotor system with coupled gear mesh［J］.Journal of Vibration，Measurement ＆Diagnosis，2012，32（4）：527－531.（in Chinese）

［10］赵岩，林家浩，曹建华.转轴系统平稳随机地震响应的变异性分析［J］.工程力学，2002，19（2）：26－31.

Zhao Yan，Lin Jiahao，Cao Jianhua.Variation analysis of shaft systens subjected to stationary random seismic excitations［J］.Engineering Mechanics，2002，19（2）：26－31.（in Chinese）

［11］赵岩，林家浩，曹建华.转子系统的平稳／非平稳随机地震响应分析［J］.计算力学学报，2002，19（1）：8－11.

Zhao Yan，Lin Jiahao，Cao Jianhua.Seismic analysis of rotor system under stationary nonstationary random earthquake excitations［J］.Journal of Computational Mechanics，2002，19（1）：8－11.（in Chinese）

［12］林家浩，钟万勰.关于虚拟激励法与结构随机响应的注记［J］.计算力学学报，1998，15（2）：217－223.

Lin Jiahao，Zhong Wanxie.Some notes on FEM and structural random response analysis［J］.Journal of Computational Mechanics，1998，15（2）：217－223.（in Chinese）