基于网格遍历曲率线的曲面网格重划算法

高云凯，张婷婷，杨肇通，罗 键

（同济大学 汽车学院，上海201804）

用一定的测量手段对实物或模型进行数据测量，然后重构实物的CAD（computer aided design）模型，实现产品设计或制造过程，即为逆向工程中实物的逆向重构过程［1］.曲面重建是采用逆向工程方法生产CAD模型的关键步骤［2］.近年来，随着计算机辅助几何设计CGAD（computer graphic aided design）及测量技术的不断发展，曲面重建技术在机械产品设计制造数字化过程中发挥着举足轻重的作用.因此，如何高效获得较高精度的重建曲面已经成为越来越多生产设计者关注的重点.

实现曲面重建较为传统的方法是基于特征面的区域分割法，具体流程如图1a所示.该方法首先分析了曲面的微分信息，提取相应的特征边或特征面并进行数据分块，最后根据不同曲面的特性利用相关多项式进行拟合，完成曲面的逆向重构.国内外许多学者在这方面研究较为深入，如Huang等［3］提出先基于网格边的方向曲率来识别边界，然后利用区域增长对网格面片进行分组的区域分割法；董明晓等［4］提出基于数据点曲率变化的区域分割法；刘胜兰［5］提出基于三角网格模型的四边域重构法等.这些算法结构简单，对特征较为明显或曲面较为规则的模型能够较好实现曲面重构的质量，但一旦涉及复杂程度较高的车身曲面或自由曲面，其适用性就会不足，原因是这些复杂曲面的特征相比一般规则区域并不明显，且较为分散.

在传统曲面重构算法的基础上，为了适应复杂曲面的重构，一些学者提出了基于曲率线追踪的曲面重构法.如图1b所示，该算法的核心是依据获取的主方向通过数值积分的方式［6］对曲率线进行追踪.如Alliez等［7］提出在曲面参数空间求解微分方程来确定追踪步的曲率线追踪法，但该算法在全局参数化的基础上进行追踪映射过程中精度难以保证，而且计算量大；庞旭芳等［8］提出利用邻域点信息建立曲率场并通过点对应的曲面微分信息来实现追踪，但曲率线在曲面特征处变化不明显；Marinov等［9］提出基于三角网格面片的局部参数化法来追踪曲率线，Kalogerakis等［10］提出在离散点云数据中直接迭代步长的空间免映射追踪法，这2种方法数值积分的过程较为繁琐，且需要复杂的数据结构进行网格密度的控制.

本文基于曲率线追踪的思想提出一种基于网格遍历的曲面网格重划算法，该算法简化了曲率线追踪过程，提出的邻域点剔除法能够灵活控制重划网格密度，保证网格分布均匀可靠，实现较好的曲面网格重划.算法的实现基于逆向过程中的三角网格模型，先采用局部参数化的一般二次曲面法来估算网格曲面的微分信息，并在此基础上建立模型的半边数据结构及提取模型的自由边界特征，最终采用基于网格遍历的曲率线算法采样.

图1 曲面重建算法流程Fig.1 Flowchart of surface reconstruction algorithm

1 三角网格顶点数据预处理

1.1 顶点主曲率场的建立

通常来讲，曲面的一阶偏导量为切向量和法向量，二阶偏导量为曲率等相关信息，曲率信息主要指主曲率及主方向.三角网格顶点的主曲率为该点所有法曲率中的最大值与最小值，主方向则为主曲率对应法平面上的切向量，它们都是曲面重要的微分几何特性.因此，确定三角网格顶点的离散微分量是网格重划的基础.

本文采用局部一般二次曲面法［5］来确定网格顶点的主曲率场.空间任意复杂曲面的局部形状都可由一般二次曲面片S（u，v）=（u，v，h（u，v））来近似拟合，其中S（u，v）是一般二次曲面片在局部坐标系下的参数形式，且二次多项式h（u，v）的数学表达式为

式中：u，v，h分别为局部坐标系puvh中u，v，h轴对应的坐标值；A，B，C，D，E，F为二次多项式系数.

对于离散网格的任意顶点P=｛pi｝，pi∈R3，i为网格顶点编号，i∈｛1，…，N｝，N为网格顶点数.本文采用质心面积夹角法［11］来估算顶点的法矢Npi.以Npi为局部坐标系的h轴建立一组单位正交基｛u，v｝，uv平面垂直于h轴，形成局部坐标系puvh.利用三角网格的拓扑关系，分别选取顶点对应的二阶邻域点集，投影至建立好的局部坐标系puvh中，作为曲面拟合的样本点.

在获取邻域点的局部信息后，二次曲面片就可通过加权最小二乘法来拟合.

式中：i为当前网格顶点的编号；j为对应的邻域点编号；uj，vj，hj为以点i为原点的局部坐标系puvh下j的坐标值；ωij为权值.

权值的分配按照邻域点pj与中心点pi的距离来确定，即

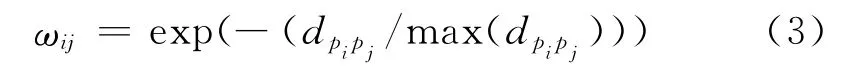
式中：dpipj为邻域点pj距顶点pi的距离，max（dpipj）为所有邻域点距顶点pi的最大距离.二次多项式的系数可由法方程来求得.

在获取离散顶点pi的局部最佳拟合多项式后，可用原点p（u=0，v=0）的微分特性来求解离散顶点的微分量，即通过拟合多项式的系数和微分几何的相关定义来确定主曲率及主方向.

1.2 自由边界的识别

自由边界是半封闭模型的重要特征之一，它既是曲率线追踪的终止条件，又是网格重划的起点或终点.自由边界不但可以保证网格重划的完整性，而且在曲面性质、受力分析等方面也起到了重要作用.因此，该特征需要从模型中提取出来，进而为后期的算法做准备.

根据半边结构的特性，利用初始化的数据结构可提取模型的自由边界.首先，遍历模型的半边数组，判断该半边的对边是否存在；若存在，则该边就不是自由边界；若不存在，则该边为自由边界，将其标记并存储在自由边数组中.

在查找完所有网格的自由边界后，同样利用半边结构的特性对自由边数组进行排序.如图2所示，设a为自由边数组中的第1个元素，a的下一个半边为b，b的对边为d，f为d的下一个半边，由此找到自由边数组中a的下一个元素f，以此类推，直至回到a，最后完成当前数组的排序.每组自由边界均为闭环.

图2 自由边界的识别Fig.2 The detection of free boundary

2 网格遍历的曲率线追踪

曲率线分为最大曲率线及最小曲率线.由定义可知，最大曲率线上每个点的切向量均与当前点的最大曲率的曲面主方向共线；同理，最小曲率线上每个点的切向量均与当前点最小曲率的曲面主方向共线［7］.最大曲率线和最小曲率线相交成直角，构成曲面上的一张正交网［12］，若对曲率线两两求交，则连接交点就会形成曲面的重划网格.基于曲率线追踪的曲面重构算法效率高、效果好，能够实现较少的人机交互，适用范围广.

本文提出基于网格遍历的曲率线追踪算法，算法的核心是：沿追踪点的主方向将该点投影至二维参数平面来寻找下一个追踪点，且所有的追踪点均位于三角网格面片的顶点或边.

曲率线追踪的过程分为沿最大、最小主方向的追踪.在追踪最大主方向时，首先设定所有的网格顶点为曲率线段的种子点集，然后在追踪每一组最大的曲率线段时将标记过的网格顶点从种子点集中剔除，最后直至种子点集为空才完成最大曲率线段的采样.同理，重新设定所有的网格顶点为曲率线段的种子点集，按上述步骤完成最小曲率线段的采样.

2.1 曲率线段追踪起始点的采样

曲率比值δi=Ki，max/Ki，min记录了曲面在这一点沿不同方向的弯曲程度，其中Ki，max与Ki，min分别为点i的法曲率的最大值与最小值.显然，各向异性区域越广，主曲率方向越明显，反之则亦然.在脐点处，曲面沿各个方向的弯曲程度相同，即δi为零，此时的主曲率方向为任意方向［13］.因此，应寻找种子点集中曲率比值最大的点为每组曲率线段的追踪起始点.这里需要注意的是，追踪起始点不能为自由边界上的点，原因就在于追踪过程涉及一阶邻域三角形，而自由边界上点的一阶邻域三角形不完整，会导致无法追踪.

2.2 曲率线段的追踪

在确定曲率线段的追踪起始点后，可根据种子点的曲率信息展开各向异性区域的追踪.由于追踪点可能为网格顶点或网格边上的点，所以将追踪的起始位置分为2种情况，即基于点的追踪和基于边的追踪.

基于点的追踪采用重心坐标法来进行局部参数化［14］.首先，标记追踪点为P，Qj为其一阶邻域点，分别计算点P到Qj之间的距离dj，找到距离最大的点Q0并将其投影至过点p与法矢NP垂直的切平面上，以Q0的投影点Q′0为基准，沿着邻域三角网格面片的排列顺序（逆时针）将点P的一阶邻域点及一阶邻域边按顺序展开，形成如图3a所示的分块区域.其切平面的示意如图3b所示，θi为原三角网格面片在P处的内角，参数α满足公式（4）：

然后，投影点P处的主方向T至切平面并标记为T′，根据T′与向量PQ′0的夹角θ′来判定T′所属的分块区域，这样就可以确定下一个追踪点所属的三角网格面片.

最后，将上一步确认的三角网格面片投影至切平面形成△PQ′iQ′i+1，i∈（0，n），如图4所示，求T′与该投影三角形的交点K′及K′到其所在边的2个顶点的距离比dQ′2K′/dK′Q′1映射关系来获取下一个追踪点K所在三角网格边上的位置.

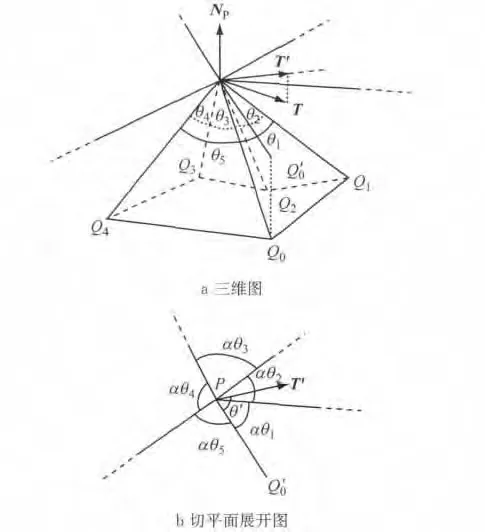
图3 重心坐标法的局部参数化示意Fig.3 Local parameterization using barycenter coordinates method

图4 当前追踪点P的邻域三角网格投影示意Fig.4 The projection diagram of current tracking point on neighborhood triangular meshes

基于边的追踪采用基平面展开法来进行局部参数化［15］.基平面是指当前追踪步的前一个追踪线段所在的三角网格面片，即第n步追踪的曲率线段所在的网格面片为基平面，则第n+1步追踪的网格面片就为目标平面，具体示意如图5所示.假设点K为当前某一边上的追踪点，点P为点K的前一个追踪点，那么线段KP所在的三角网格就是基平面，这里记为△P0P1P2；与此同时，与点K所在边的相邻三角形就为目标平面，即△P1P2P3.点K的下一个追踪点的求解方式也在切平面上展开，首先，将点P1，P2，P3及K的主方向TK依次投影至过点K的切平面上，从而获得目标映射平面△P′1P′2P′3及投影后的主方向T′K；然后，在二维平面△P′1P′2P′3内过点K沿T′K的方向求下一条边上的映射追踪点L′；最后，根据点L′在边P′3P′2的位置来逆映射出追踪点L在边P3P2上的位置.

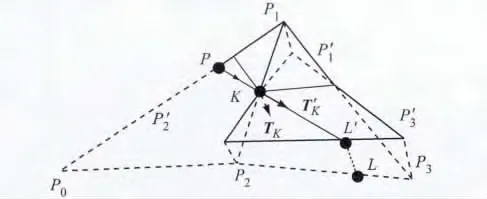
图5 基平面展开法的局部参数化示意Fig.5 The base plane parameterization diagram using barycenter coordinates method

追踪点微分信息的求解可分为2种情况，即若追踪点为网格顶点，则其主曲率及主方向可直接获取；若追踪点为网格边上的点，则可用线性插值法来确定.

2.3 曲率线段的分布

曲率线段的追踪流程如图6所示.首先，对种子点集进行点采样，用以确定曲率线段的追踪起始点并对其进行标记；然后，展开各向异性区域的曲率线分布并分析追踪点位置，从而有针对性地展开基于点、边的追踪算法，以便确定下一个追踪点的位置.这里需要注意，若下一个追踪点与邻近网格顶点的距离小于用户设定的阈值（设L为当前追踪点所在三角网格的边长，本文取0.05L），则将当前追踪点替换为邻近的网格顶点.

图6 曲率线段的追踪流程Fig.6 Flowchart of curvature line tracking

当每组曲率线段的追踪遇到下述2种情况时，追踪终止.

（1）追踪到敏感区域.所谓敏感区域，是指已被追踪过的区域，其微观表现为数据结构中的敏感性.一个三角网格面片有2个方向的敏感性，即最大主曲率方向敏感与最小主曲率方向敏感.如果被定义在最大主曲率方向上敏感，则当最大主曲率线段追踪到该三角网格面片时子追踪步应立即停止；同理，当最小主曲率线段追踪到最小主曲率敏感的三角网格面片时，该子追踪步也应当停止.简单地说，每追踪到一个三角网格面片时，都要对该网格面片进行标记.

（2）追踪线段到达模型的自由边界.在曲率线段追踪完毕后，需要设定曲率线段的密度来控制网格分布的大小.曲率线段的密度是指2条相邻的曲率线段间的空间距离大小，其分布将会影响网格重构的质量.因此，在进行曲率线段的追踪时应考虑它在给定位置处的理想密度［4］.本文提出一种动态控制曲率线段密度的方法，即实时邻域点剔除法.该算法的核心是：在每条追踪线段完毕后，将追踪线段所在的三角网格m阶邻域点进行标记（m为用户自定义，本文选取m=5），标记过的点不会成为追踪起始点.

如图7所示，假设顶点A为某三角网格模型中曲率比值最大的点，B，C，D紧随其后；3组线段为追踪的曲率线段.那么，当完成以点A为追踪起始点的子追踪步后，接下来应选取除A外的曲率比值最大点，则B应作为第2组曲率线段的追踪起始点，但由于点B，C均处在第1组曲率追踪线段所在网格面片的m阶邻域范围内，所以下一组曲率线段的追踪起始点为不在范围内的点D.

图7 曲率线段的密度控制示意Fig.7 The diagram of curvature line density control

按上述追踪方法沿网格顶点的最大、最小主方向循环进行曲率线段的追踪，直至形成正交的主曲率网格.对网格上所有的节点进行求交，这些交点便是重划网格的采样点，而重划的网格边则为采样点的主曲率线段，由此来获取逆向过程中曲面模型的重划网格.

3 算法应用实例分析与比较

通过一些三角网格模型的实例，如管道、车门、车身翼子板等来测试曲面网格的重划算法，从而实现自曲率估算→自由边界特征的提取→曲率线段的追踪→网格重划等一系列过程.图8～10为算法应用实例，图11及12为相关算法与本文算法实例比较.

本文采用绝对值分组法来显示曲率的估算结果，根据人眼对颜色的分辨能力，按照色带由红到绿再到蓝，亮度由暗到亮再到暗的变化方式选出10种最具代表性的颜色来绘制曲率，相应的颜色及RGB（red，green，blue）值为：紫（0.5，0，0）、红（1.0，0，0）、橙（1.0，0.5，0）、浅红（1.0，0.5，1.0）、浅黄（1.0，1.0，0.5）、绿（0，1.0，0）、浅蓝（0，1.0，1.0）、蓝绿（0.5，0.5，1.0）、蓝（0，0，1.0）、青（0，0.5，0.5）.曲率值由大到小等分为10组，对应上述10种颜色由亮到暗变化.

图8 管道的网格重划过程Fig.8 The surface remeshing of pipe

图9 车门的网格重划过程Fig.9 The surface remeshing of car door

如图8b，9b，10b所显示的曲率估算结果来看，在圆角、孔洞等过渡曲面处色彩鲜明，曲率值明显较大，而在平面或曲面较为平缓区域曲率渲染色彩位于曲率值较小的范围内，颜色较暗，模型各区域的曲率渲染色彩分布充分反映曲面曲率值大小，因此曲率估算结果较接近真实值.如图8c，9c，10c所示，管道的上下端的自由边界，车门及翼子板的外围自由边界都能够完全被识别，因此利用半边数据结构查找自由边的方法为后期曲率追踪终止条件的设定奠定坚实的基础.最后，如图8a，8d，8e，8f，9a，9d，9e，9f，10a，10d，10e，10f所示，最大、最小曲率线沿曲率线的主方向展开形成规则的曲率线网，网格的大小分布合理；曲率较大位置（圆角或倒角处）的网格分布较密；曲面平坦处分布较疏.所以，对特征不明显或较为分散的复杂曲面，该算法能够提供理想的曲面网格重划结果.

图10 车身翼子板的网格重划过程Fig.10 The surface remeshing of fender

如图11所示，维纳斯模型在嘴角右下方有凹陷，头部发型复杂，脖颈曲面较为规则.相比文献［8］算法，本文算法不仅在凹陷处实现较为规则的网格重划，且对不同复杂程度的曲面都具有良好的适应性.

图11 文献［8］算法与本文算法的比较Fig.11 Comparison with reference［8］

如图12所示，本文算法已经达到了通过追踪来分割离散曲面的目标，兔子网格密度能按照曲面的变化合理分布，兔子后背处网格较头部更密集，体现了其肌肉的纹理变化.但是要获得高质量的结果，仍需要增加网格简化（mesh simplification）、凸分解（convex decom-position）等后处理步骤.

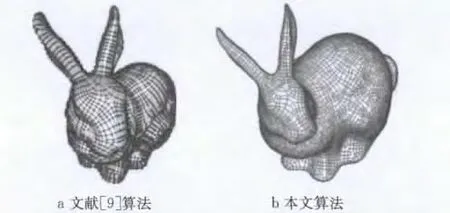
图12 文献［9］算法与本文算法的比较Fig.12 Comparison with reference［9］

4 结语

主要研究了逆向工程中曲面网格的重划算法.首先，采用局部一般二次曲面法建立了三角网格顶点的主曲率场，并提出了基于半边结构的自由边界识别法，该方法能够完全识别出模型的自由边界；然后，提出了一种基于网格遍历的曲率线段追踪法，该方法采用了将目标三角网格投影至切平面的二维参数化法，准确、高效地追踪到了曲率线段；最后，在追踪过程中提出了基于邻域点剔除思想的曲率线段动态密度控制法.

本文提出的方法能够在特征不明显或结构复杂的网格曲面上进行曲率线段的追踪，并实现密度适中的曲率线分布，从而最大限度减小了后期重构曲面与原始网格模型间的差距，为三角网格模型的曲面重建提供了保障.

［1］ 邢健，付大鹏，郝德成.基于逆向工程的汽轮机叶片型面CAD建模方法的研究［J］.机械设计与制造，2011（5）：223.XING Jian，FU Dapeng，HAO Decheng.Study of CAD modeling for turbine blade profile based on reverseengineering［J］.Machinery Design &Manufacture，2011（5）：223.

［2］ 盛忠起，蔡光起.逆向工程及曲面重建技术［J］.机械设计与制造，2001，12（6）：102.SHENG Zhongqi，CAI Guangqi.Reverse engineering and surface reconstruction［J］.Machinery Design &Manufacture，2001，12（6）：102.

［3］ Huang J B，Menq C H.Automatic data segmentation for geometric feature extraction from unorganized 3-D coordinate points［J］.IEEE Transactions on Robotics and Automation，2001，17（3）：268.

［4］ 董明晓，郑康平，姚斌.曲面重构中点云数据的区域分割研究［J］.中国图象图形学报，2005，10（5）：575.DONG Mingxiao，ZHENG Kangping，YAO Bin.Research on point cloud data segmentation in surface reconstruction，2005，10（5）：575.

［5］ 刘胜兰.逆向工程中自由曲面与规则曲面重建关键技术研究［D］南京：南京航空航天大学，2004.LIU Shenglan.Research on key technology inreconstruction of free-form ®ular surfaces in reverseengineering［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2004.

［6］ Allize P，Ucelli G，Gotsman C，et al.Recent advances in remeshing of surface［M］.Mathematics and Visualization.Berlin：Springer-Verlag，2008.

［7］ Alliez P，Cohen S D，Devillers O，et al.Anisotropic polygon remeshing［J］.ACM Transaction on Graphics（TOG），2003，22（3）：485.

［8］ 庞旭芳，宋展.散乱点云曲率场的计算［J］.中国科学院先进技术研究通报，2010，4（7）：39.PANG Xufang，SONG Zhan.High-throughput multi-antigen immunoassays on a microfluidicchip［J］.Bulletin of Adavanced Technology Research，2010，4（7）：39.

［9］ Marinov M，Kobbelt L.Direct anisotropic quad-dominant remeshing［C］//Proceedings of Pacific Graphics.Seoul：IEEE，2004：207-216.

［10］ Kalogerakis E，Nowrouzezahrai D，Simari P，et al.Extracting lines of curvature from noisy point clouds［J］.Computer-Aided Design，2009，41（4）：282.

［11］ 齐宝明.三角网格离散曲率估计和Taubin方法改进［D］.大连：大连理工大学，2008.QI Baoming.Curvatures estimation and the improvementof Taubin’s method on triangular mesh［D］.Dalian：Dalian University of Technology，2008.

［12］ 朱心雄.自由曲线曲面造型技术［M］.北京：科学技术出版社，2000.ZHU Xinxiong.Curve and curved surface model technology［M］.Beijing：Scientific and Technical Publishers，2000.

［13］ 朱为鹏，高成英，罗笑南.全局各向异性四边形主导网格重建方法［J］.软件学报，2012，23（5）：1305.ZHU Weipeng， GAO Chengying，LUO Xiaonan.Global anisotropic quad-dominant remeshing［J］.Journal of Software，2012，23（5）：1305.

［14］ Welch W，Witkin A.Free-form shape design using triangulated surfaces［C］//SIGGRAPH94 Conference Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques.Orlando：SIGGRAPH，1994：247-256.

［15］ Sorkine O，Cohen D，Goldenthal R，et al.Bounded-distortion piecewise mesh parameterization ［C］//Proceedings of the Conference on Visualization’02.Washington D C：IEEE，2002：355-362.