变系数模型的核权二次推断函数方法

李静茹，钱伟民

（同济大学 数学系，上海200092）

1 引言

非参数回归模型由于其形式自由、对数据的假定要求小、稳健性高等优点而越来越受到重视.但常用的非参数估计方法在估计多元的非参数回归函数时需要大量数据，估计极不稳定，人们称这种现象为“维数祸根”.对于高维数据近年来半参数回归分析受到广泛关注，其中变系数模型是一个研究的热点，它具有结构简单、容易解释、应用广泛等特点.

本文讨论变系数模型：

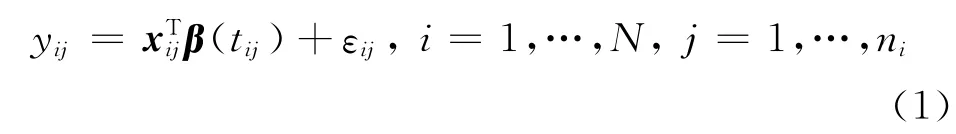
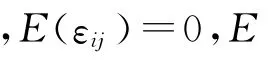
变系数模型是一般线性模型的推广，由Hastie和Tibshirani［1］提出.对于函数项系数的估计，主要方法有核估计最小二乘方法；光滑样条补偿最小二乘法（Wahba［2］）；局部多项式法［3-5］等.Hoover等［6］将变系数模型推广到纵向数据的分析，给出了函数项系数的局部多项式估计.

在非参数纵向数据的局部模型中，考虑相关结构十分重要.Wang［7］、Lin等［8］证明了使用真正的相关结构的核光滑样条方法要比使用独立结构得到的估计更有效.但在实际中方差结构通常是未知的，经验上估计非构造的相关结构很困难，存在可能非正定、不可逆和冗余参数多等对估计至关重要的问题.采用Liang等［9］提出的使用工作相关矩阵的广义估计方程方法，又会产生大量的不必要的待估参数.Qu等［10］提出了二次推断函数方法，用一系列基矩阵的线性组合来逼近工作相关矩阵.这一方法的好处是可以把线性组合中的系数视为冗余参数，不予理睬，而通过最小化二次推断函数，直接获得参数的估计.Qu和Li［11］将这一思想应用于纵向数据变系数模型，通过惩罚样条方法得到函数系数的估计.

本文利用了二次推断函数的思想，使用局部多项式（一阶）光滑法建立了纵向数据变系数模型的核权二次推断函数，基于此得到函数系数的估计，并证明了估计的渐近性质.在随机模拟中对核权二次推断函数估计与非构造协方差结构的最小二乘估计做了比较.Lin和Carroll［12］指出，最渐近有效的核估计是在完全忽略样本相关性得到的.但在实际中充分大的样本容量和趋向于0的窗宽都不易达到，模拟中会发现独立结构下的估计并不总是最好的.由此可以给出了一种选取核权二次推断函数方法窗宽的一种方法，以及如何确定拟合的工作相关结构.

2 估计方法

3 渐近性质

假设以下条件成立：

条件1：系数函数βk（·）有连续二阶导数，k=1，…，p.

条件2：tij，i=1，…N，j=1，…ni独立同分布，密度函数f（t）有连续一阶导数.

定理证明略去.

综上，使用局部多项式拟合构造了核权二次推断函数，可以证明由此得到的函数系数具有渐近正态性和强相合性.与Qu等［11］的使用惩罚样条方法所得到的的结论是类似的.与样条方法相比，局部多项式拟合的计算速度略慢，但却具有同时估计系数函数及其各阶导数的优势.样条方法通过控制节点数和惩罚系数来控制拟合的误差与光滑度，而局部多项式估计是选取合适的窗宽来完成这一任务的，两者均是非参数回归的主要方法.同时局部多项式估计时线性估计类中的最佳估计，它具有几个吸引人的特点，例如它有好的最小最大性质，可适用于各种设计，如随机设计和固定设计等；它容易解释、实施并适应于导数的估计等.

4 随机模拟

数据生成模型类似于Qu等［11］中的例2，具体如下：

（3）εi～MV（0，Σi），Σi为对角线为2，其余位置为1.6的ni阶方阵.

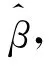
图1 固定窗宽h＝1.2时，100次模拟的MADE比值散点图Fig.1 Scatter diagrams for the MADE’s ratios ofrespectively in 100simulations with fixed h＝1.2

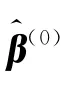
R h 0.4 0.8 1.2 1.6 2.0 2.4 1 1.078 0.98 1.00 1.04 1.00 0.98 2 1.09 0.94 0.85 0.80 0.87 1.03 3 1.25 1.05 1.06 0.96 0.92 0.96 4 1.16 1.21 1.05 0.99 0.97 1.02 5 0.99 0.99 0.89 0.98 1.11 1.25 1 1.10 0.99 0.94 0.99 1.10 1.21 2 1.10 0.95 0.91 0.98 1.13 1.25 3 0.95 0.90 0.93 0.96 1.06 1.15 4 1.06 1.05 0.98 0.99 1.06 1.16 5 1.06 0.93 0.99 1.13 1.30 1.44 R=MADE，β^ex MADE，β^（0）N=100 R=MADE，β^QIF4 MADE，β^（0）N=100

序号 R h0 hQIF4序号 R h0 hQIF4 1 1.03 1.53 1.80 11 0.86 1.53 1.80 2 1.01 1.53 1.6212 1.11 1.35 1.80 3 0.93 1.53 1.8013 1.00 1.62 1.71 4 0.89 1.35 1.3514 0.89 1.44 1.71 5 1.28 1.62 1.5315 0.92 1.62 1.80 6 0.93 1.53 1.8016 1.04 1.80 1.53 7 0.95 1.44 1.8017 1.01 1.53 1.62 8 1.20 0.99 0.9018 0.90 1.44 1.80 9 1.17 1.80 1.7119 1.03 1.62 1.44 10 1.15 1.26 1.3520 0.97 1.62 1.80

众所周知，核估计中窗宽h的选择至关重要，h选择过大，会使估计的偏差加大，h选择过小虽然可以减少估计的偏差，但却增加了估计的方差，造成“过拟合”的现象.通过以上模拟可以看到，使用核权二次推断函数方法，选择合适的h，在局部范围内适当引入了数据间的相关结构，既可以保证估计的效果足够令人满意，也不会造成“过拟合”的结果.

［1］ Hastie T J，Tibshirani R J.Varying-coefficient models（with discussion）［J］.Journal of the Royal Statistical Society Series B，1993，55（4）：757.

［2］ Wahba G.Spline models for observational data ［M ］.Philadelphia：SIAM，1990.

［3］ Stone C J.Consistent nonparametric kernel regression［J］.Annals of Statistics，1997，5（4）：595.

［4］ Cleveland W S.Robust locally weighted regression and smoothing scatterplots［J］.Journal of the American Statistical Association，1979，74：828.

［5］ Fan J.Design-adaptive nonparametric regression［J］.Journal of the American Statistical Association，1992，87：998.

［6］ Hoover D R，Rice J A，Wu C O，et al.Nonparametric smoothing estimates of time-varying coefficient models with longitudinal data［J］.Biomatrika，1998，85：809

［7］ Wang N.Marginal nonparametric kernel regression accounting for within-subjuct correlation［J］.Biometrika，2003，90：43.

［8］ Lin X，Wang N，Welsh A H，et al.Equivalent kernels of smoothing splines in nonparametric regression for clustered/longitudinal data［J］.Biometrika，2004，91：177.

［9］ Liang K Y ，Zegger S L.Longitudinal data analysis using generalized linear models［J］.Biometika，1986，73：12.

［10］ Qu A，Lindsay B G，Li B.Improving geralised estimating equations using quadratic inference functions［J］.Biometrika，2000，87：823.

［11］ Qu A，Li R.Quadratic inference function for varyingcoefficient models with longitudinal data［J］.Biometrics，2006，62：379.

［12］ Lin X，Carroll R J.Nonparametric function estimation for clustered data when the predictor is measured without/with error［J］.Journal of the American Statistical Association，2000，95：520.

［13］ Wedderburn R W M.Quasi-likelihood functions，generalized linear models，and the Gauss-Newton method［J］.Biometrika，1974，61：439.

［14］ Qu A，Lindsay B G.Building adaptive estimating equations when inverse-of-covariance estimation is difficult［J］.Journal of the Royal Statistical Society Series B，2003，65：127.