一种旋转调制器成像技术研究

魏 星 王 锋 肖无云 艾宪芸 张 斌 张 磊 马新华

（防化研究院 国民核生化灾害防护国家重点实验室 北京102205）

一种旋转调制器成像技术研究

魏 星 王 锋 肖无云 艾宪芸 张 斌 张 磊 马新华

（防化研究院 国民核生化灾害防护国家重点实验室 北京102205）

γ射线成像技术在核安全领域正逐渐受到人们重视。为了在提高成像系统灵敏度的同时尽可能降低系统复杂度和成本，一种采用非位置灵敏探测器的旋转调制器成像技术被首次引入到核监测技术领域。为研究该技术的理论基础、调制传递函数、图像重建方法等，开展了仿真研究工作。结果表明，同等探测器面积下，旋转调制器成像系统的灵敏度约为编码孔成像系统的62%，但旋转调制器成像系统的探测器数量扩容性很强，能在系统复杂度增加不多的情况下提高探测器总面积，从而极大提高系统灵敏度；通过迭代重建方法能得到超过系统几何角度分辨率的目标图像，在像距80cm，探测器直径3.8cm时，重建图像的角度分辨率约为0.8°。最后根据仿真结果提出了适于小型车辆或机器人等移动平台的原理性装置的设计方案。

γ射线成像，旋转调制器，系统灵敏度，图像重建，迭代法

国际原子能机构(IAEA)非法贩运数据库(ITDB)的数据[1]表明，涉及核及其他放射性材料的非法贩运、遗失、盗窃和其他非法活动或事件确实存在，证明了核和辐射恐怖主义的潜在危险。2011年日本福岛核事故的发生，再一次使核能安全成为全球关注的焦点。我国拥有大量放射源、射线装置、核设施等[2]，且已经规划扩展核电规模。这表明我国面临的核安全形势将会越加严峻，也对我国核监测能力建设提出了更高要求。因此以技术革新的方式增强我国核监测水平势在必行。γ射线成像技术正是一种可在非接触或非拆卸方式下发现、定位、鉴别危险放射性目标的高端核监测技术，是提升核监测技术水平的关键技术之一。

20世纪90年代，美国劳伦斯·利弗莫尔国家实验室(Lawrence Livermore National Laboratory, LLNL)研制的GRIS[3]系统标志着γ射线成像技术被应用于核监测领域。此后，国外各大公司相继推出具有γ射线成像功能的产品。我国中国原子能科学研究院、清华大学、中国科学院高能物理研究所等单位的相关研究组也在这方面开展了研究，有些已经取得了比较成熟的研究成果。这些在研或产品化的γ射线成像系统，基本采用了源于天文学研究的编码孔(Coded Aperture, CA)成像技术。CA成像过程包括空间编码和解码两步，因此是一种多重技术。编码孔技术的缺点在于实现具有大面积探测器的成像系统的代价较大。

旋转调制器(Rotating Modulator, RM)成像技术是Durouchoux等[4]于1983年提出的一种成像技术，初衷是为了研制硬X射线、γ射线天文望远镜。RM技术目前仅在天文学领域处于实验研究阶段[5]，我国尚无关于该技术的研究。陈勇等[6]曾对RM成像技术的前身旋转调制准直器(Rotating Modulation Collimator, RMC)技术进行过研究。与CA成像技术一样，RM成像技术也属于多重技术，其区别在于RM成像属于时间调制技术。RM成像系统采用一个栅条状准直器和多个非位置灵敏探测器(图1)。准直器围绕其中心以角频率ω转动，栅条投影会周期性扫过每个探测器，使得探测器输出呈现按时间周期性调制的起伏变化。通常栅条宽度和栅条间隔相等，等于探测器直径，因此RM准直器透光率达到50%，与CA相当。RM系统的几何角度分辨率Δθ由栅条间隔b和像距L（准直器到探测器的距离）之比决定：

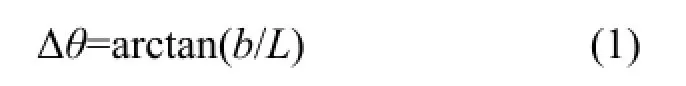
与CA系统的探测器像素尺寸比较，RM系统所用的探测器直径很大，为了保证整个系统的尺寸重量等指标，系统的像距又不可能很大，所以RM系统的几何角度分辨率通常较低，通过适当的图像重建方法，可以提高角度分辨率，达到或超过CA系统的水平。

RM系统的最大优点在于采用非位置灵敏探测器阵列来构成具有位置灵敏探测功能的系统，其数量扩容性强，即系统探测器总面积扩展性强。由于非位置灵敏探测器无需位置分辨能力，因此探测器厚度不受闪烁光弥散效应等限制，由此可以扩展RM系统探测的能量范围。时间调制的特性使得RM系统能够很好地探测本底随时间的变化，消除本底由于时间上的不均匀引起的图像质量下降。此外，RM系统中个别探测器失效除了降低系统整体灵敏度外，不会对重建图像造成影响；而CA系统中如果探测器失效则会使得重建图像失真，甚至根本无法得到图像。正是因为RM成像技术的这些优点，使其在建造大面积γ射线成像探测系统中具有优势，因此针对弱源、远距离等情况下的γ射线成像应用，选择了采用RM成像技术。

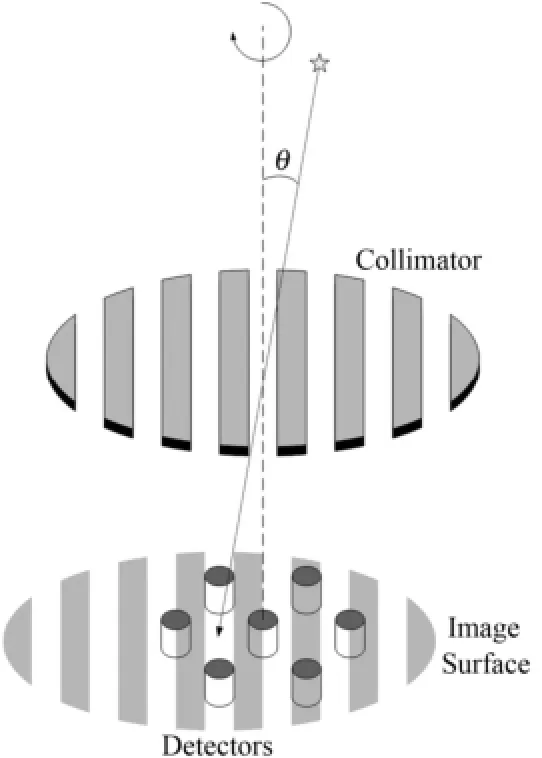
图1 RM成像系统示意图Fig.1 Rotating modulator imaging system.

本文介绍了RM成像数学模型推导和图像重建方法，对RM成像技术开展了仿真研究，根据仿真结果，给出了一种原理性装置的设计方案。

1 RM成像数学模型推导

RM成像数学模型推导可参考文献[4]，用d表示探测器编号，t表示时间，则探测器输出表示为Od(t)。用n表示目标空间像素索引，则目标空间源强度分布表示为S(n)。目标空间位于像素n的点源在时刻t向探测器d的调制传递函数表示为Pd(n,t)，于是可得RM系统探测过程的数学表达为：

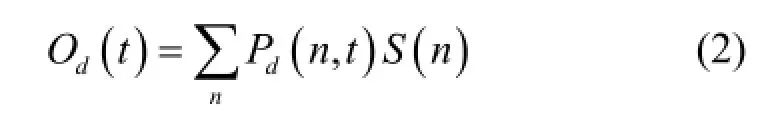
为了计算调制传递函数，建立如图2所示的坐标系(x, y)和(x′, y′)。其中(x, y)坐标系是准直器相对于无限远处位于极角θ、方位角ψ的点源的投影确定的坐标系，原点为投影中心；(x′, y′)坐标系是准直器本身确定的坐标系，原点为准直器实际位置中心。在以下推导中，为简化表达式，两个坐标系都以探测器直径为单位长度。

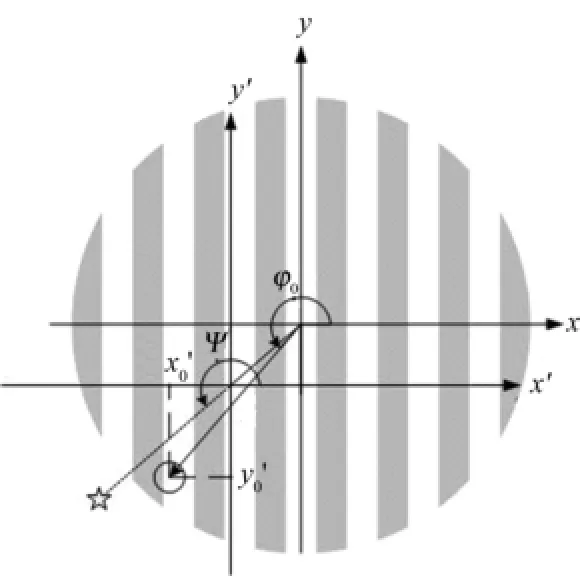
图2 RM调制传递函数计算坐标系Fig.2 Coordinates for calculation of RM modulating function.

栅条阴影对探测器的遮挡区域为一个弓形区域，在其他条件一定的情况下，探测器计数率由该弓形区域面积决定，而区域的面积与其拱高相关，即与探测器中心在(x, y)坐标系下的x坐标相关，可由探测器中心在(x, y)坐标系下的极坐标(r, φ)计算：

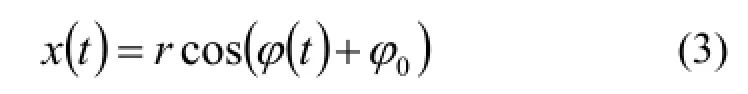
r和φ0由像距L、极角θ、方位角ψ和探测器在(x′, y′)坐标系的坐标(x0′, y0′)确定：

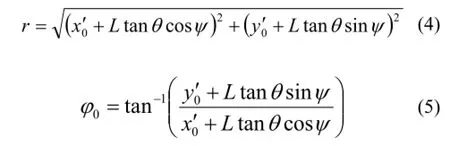
由于探测器直径、栅条阴影宽度和阴影间隔都为1，因此根据x(t)计算弓形阴影拱高x*(t)的公式为：

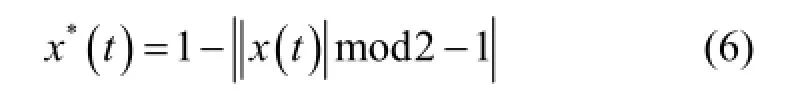
由此可得物面空间某点n到探测器d的调制传递函数：

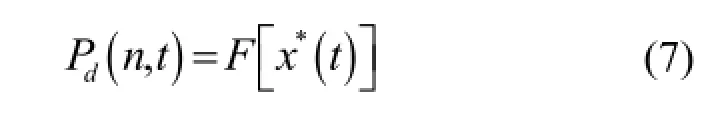
式中，d是探测器索引；n是物面空间点源位置的索引；t是时间；F(τ)表示探测器未被遮挡区域所占的面积比例，F(τ)=1-F*(τ)。这里F*(τ)是弓形阴影面积所占比例：

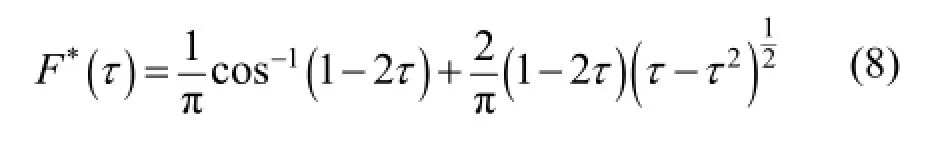
2 图像重建

在已知系统调制传递函数和测量数据后，图像重建的目的就是通过方程(2)求解S(n)，但测量数据属于时间域，方程难以求解。为了将数据从时间域转换到图像空间，采用互相关法。假设目标空间划分为N个像素，测量时间离散化为M个采样周期。那么对每个探测器，Pd是1×N的矩阵，矩阵中每个元素是一个M维向量。探测器输出Od也是M维向量。S(n)是N×1的矩阵。将方程(2)两边同时乘以Pd的转置PdT，则互相关法计算公式：

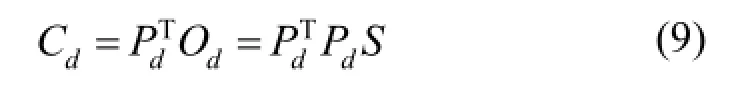
通过式(9)将时间域测量数据Od转换到图像空间，得到由探测器d的输出数据重建的互相关图像Cd。令Ad=Pd，则矩阵乘法中，两个矩阵元素的乘积是对应的两个向量的点积和：

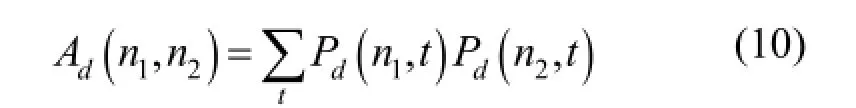
式中，n1、n2的取值范围是1-N。根据式(10)，式(9)写为：

将各探测器的互相关图像求和，即得到总的互相关图像：

但对各探测器逐一求解效率较低，根据矩阵乘法的性质，令：

可得：

虽然通过互相关法，得到图像C，但C呈现出源所在位置有较强的峰，而四周有波纹状起伏边缘的形式。为了获得更好的重建图像，必须对C进一步处理，消除波纹状边缘。式(14)是一个典型的投影方程，源图像S通过传递矩阵A投影到观测图像C，在C和A已知的情况下，有很多方法可以求解这种方程，得到源图像S的估计。在众多方法中，一类最常用的方法是迭代法。在RM成像的图像重建中，采用了Gauss-Seidel代数迭代重建算法，其迭代公式为：

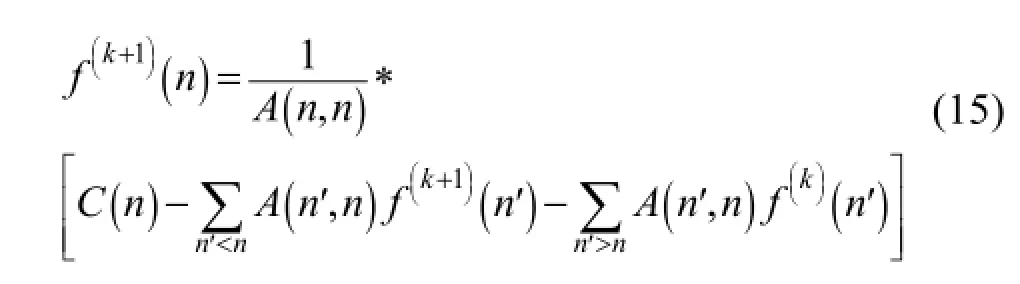
代数迭代算法不能直接考虑数据中的噪声，对噪声和传递系数的误差等敏感，迭代过程中容易出现噪声放大，而在重建图像中出现伪像，或者使真实信号淹没在噪声中，无法得到正确图像。为解决这一问题，采用了一种噪声补偿代数迭代重建算法(Noise-Compensating Algebraic Reconstruction, NCAR)[7]，该算法迭代时加入随机噪声补偿，数据中的噪声由于随机噪声相互叠加被消除，最后只在真实源位置留下相应的峰，即真实源的图像。NCAR在迭代过程中用C(k+1)替代C，对含噪声的数据进行补偿。

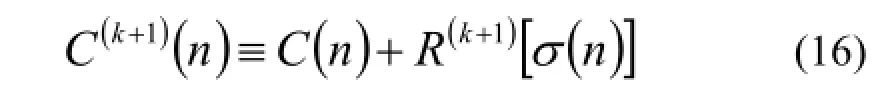
式中，R[σ]是服从均值为零，标准差为σ的正态分布的随机变量；σ是互相关图像C中各像素的误差。如果误差仅由泊松分布引起的，则

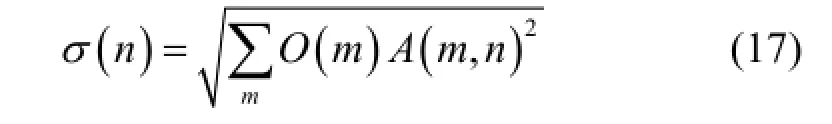
式中，O(m)表示向量的第m个分量。NCAR迭代公式为：

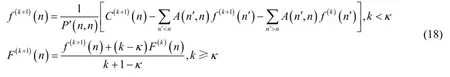
F(k+1)即是源图像的最终估计。为了更直观解释NCAR逼近源图像的过程，并解释如何确定κ，定义归一化β函数如下：

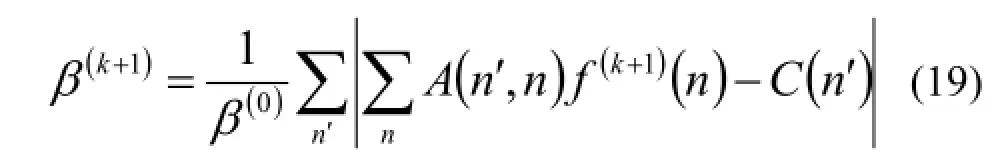
β(k+1)是第k+1次迭代的重建图像对互相关图像的残差和，表明了重建图像在传递矩阵为A的情况下与互相关图像的相似程度，图3是用NCAR算法重建图像时，β值与迭代次数之间的关系曲线。

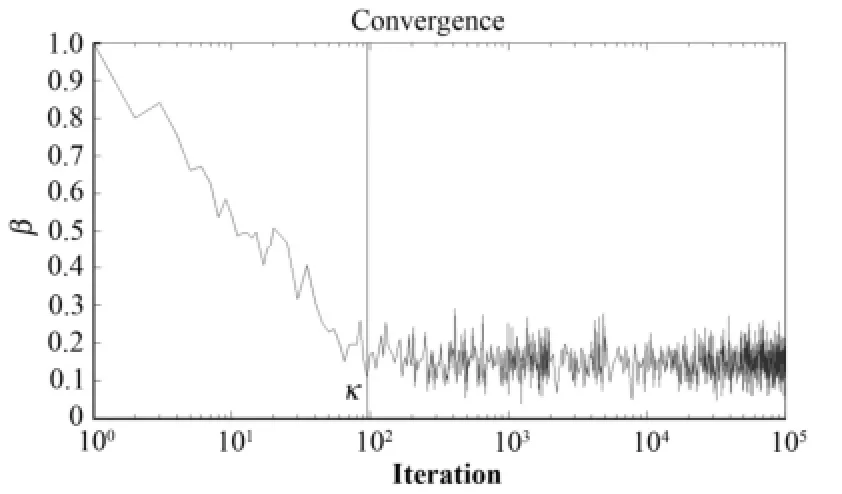
图3 β-迭代次数曲线Fig.3 β, plotted against iteration number.

随迭代次数增加，重建图像逼近互相关图像，迭代次数达到κ后，逼近程度在某一值附近起伏，将此后所有迭代结果求平均，达到噪声补偿的目的，这也是式(18)的迭代过程分成两部分的原因所在。这种求平均的方法要求迭代次数多，因此NCAR算法计算速度较慢。此外，相对于CA成像技术采用二维编码、解码矩阵重建图像，RM技术的图像重建迭代公式是一维形式，也导致RM技术的图像重建过程计算量大，重建过程复杂。

3 仿真

仿真工作采用了蒙特卡罗粒子输运程序MCNP4和数学软件Matlab。在Matlab中编写了调制传递函数Pd(n,t)、传递矩阵A和图像重建的计算程序，并仿真了理想情况下的测量数据及图像重建结果；在MCNP4中仿真了存在泊松噪声情况下的测量数据，并用Matlab计算程序重建图像。7个NaI探测器排列如图4，探测器直径4 cm，系统几何角度分辨率约为2.86°。理论上，RM系统中的探测器数量不受限制，位置可以任意排列，只要根据探测器位置计算相应的调制传递函数即可。但因为准直器旋转的原因，系统有效视场必然为圆形，因此探测器均匀排列在圆周上可以最大化利用视场范围，并使得系统对目标空间各处的灵敏度更加均匀。RM系统中探测器数量越多，系统灵敏度越高，但考虑到仿真过程中的数据处理量，选择了7个探测器的组合。

准直器转动过程中，栅条阴影对探测器的遮挡面积按转动角度以π为周期变化，因此将调制传递函数的参数t映射到转角，并将传递系数归一化。图5是计算得到的目标空间位于(θ=0°, ψ=0°)的像素向2号探测器的调制传递函数。

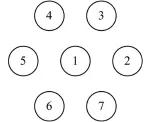
图4 探测器排列Fig.4 Detector array for simulating.

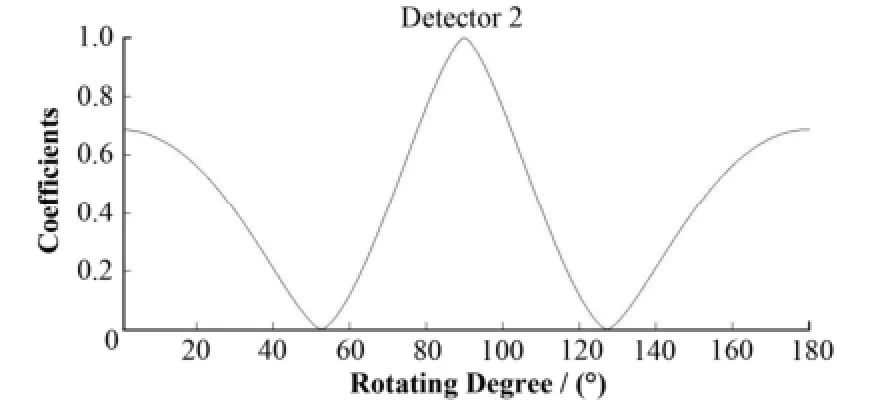
图5 调制传递函数示例Fig.5 Simulated modulating function.

仅考虑泊松噪声时，成像系统灵敏度定义为

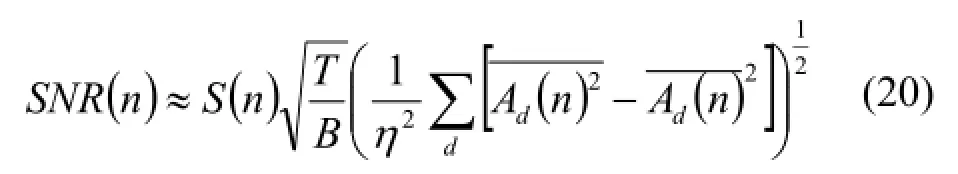
RM系统包含多个探测器，系统灵敏度为

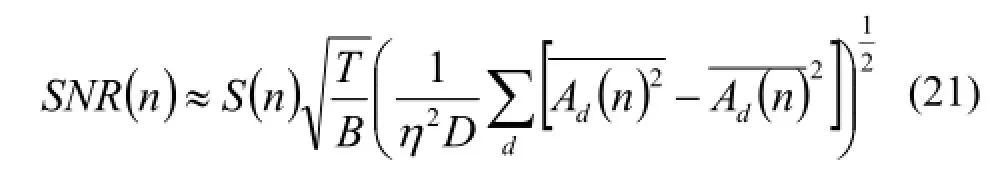
式(20)、(21)中，S(n)是位于像素n的源在探测器处引起的计数；T是测量时间；B是本底计数；D是探测器数量；η是超采样因子。对RM系统，η=1。对于CA系统，为了满足耐奎斯特采样定律，要求编码孔尺寸b至少是探测器像素尺寸a的2倍，有：

因此对CA系统，η≥1。取η=1，将CA系统传递矩阵和RM系统的传递矩阵分别代入式(20)、(21)，并以S(n)(T/B)1/2为单位，将灵敏度归一化，得到CA系统对整个目标空间的灵敏度为0.5，而RM系统对目标空间不同位置的灵敏度不同，其平均值约为0.31。可知，在探测器状态相同的情况下，RM系统灵敏度约为CA系统的62%。但是如果考虑S(n)(T/B)1/2项，则探测器面积越大，灵敏度增加越多。因此，如果扩展RM系统的探测器数量，可以提高系统整体灵敏度。图6是仿真得到的RM系统对目标空间的不同像素的归一化灵敏度值分布，左边是7个探测器的总灵敏度，右边是1号探测器的灵敏度。从1号探测器对中心像素的灵敏度为0，这是由于准直器转动过程，该像素的投影始终没有遮挡1号探测器（未调制）造成的。对每个探测器相应地都有一个不受调制的点。这也是RM成像采用多探测器组合的原因之一，以保证对整个目标空间的灵敏度都不为0。

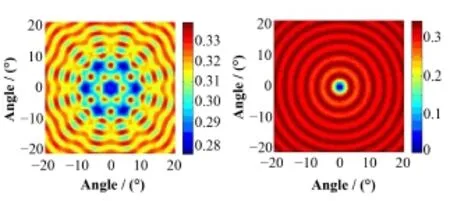
图6 归一化灵敏度Fig.6 Normalized SNR.

不含噪声时，对10 m外视野中心(θ=0°, ψ=0°)活度3.7×106Bq的137Cs源成像，准直器旋转频率5r/min，测量10 min，得到的归一化互相关图像（图7）。分别用Gauss-Seidel迭代和NCAR重建图像，迭代5000次，得到的归一化图像(图8)。由于NCAR方法迭代过程中加入的随机噪声补偿，使得重建图像中在点源周围出现随机模糊边缘，因此增加了目标源尺寸的不确定度，这是NCAR方法的一个缺点。在同样参数下，用蒙卡仿真了含泊松噪声的测量数据，在Matlab中进行重建。得到的归一化互相关图像(图9)。得到的归一化重建图像(图10)。含噪声时，Gauss-Seidel迭代出现局部噪声放大，重建图像中出现伪像。而NCAR方法抑制了伪像。

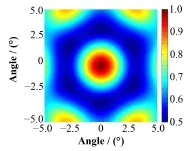
图7 理想情况中心点源的互相关图像Fig.7 Cross-correlation image for a point source at θ=0°, ψ=0° without noise.

对10 m外间隔分别为1°、0.8°、0.6°的两个137Cs点源成像，点源活度都为3.7×106Bq，准直器旋转频率5 r/min，测量时间10 min，用蒙卡仿真获取了含有泊松噪声的测量数据，之后在Matlab中对测量数据进行重建。得到的归一化互相关图像如图11所示，在互相关图中，两个点源相互重合，无法分辨。用NCAR方法重建图像，迭代次数5000次，得到的归一化图像如图12所示，为了更清楚地显示图像，选择-2° - 2°，对图像进行了局部放大。重建图像中能够较好地分辨间隔0.8°的两个点源。当两个点源间隔0.6°时，它们的重建图像相互重叠。在该仿真实验中，相对于2.86°的几何角度分辨率，NCAR方法达到约3.5倍的超分辨。

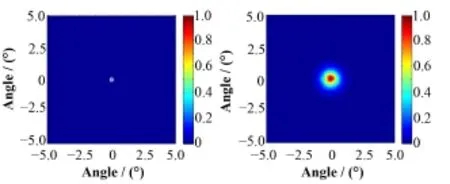
图8 无噪声情况中心点源的重建图像左：Gauss-Seidel迭代，右：NCAR迭代Fig.8 Reconstructed images for a point source at θ=0°, ψ=0° without noise. Left: Gauss-Seidel, Right: NCAR

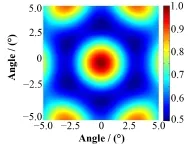
图9 泊松噪声情况中心点源的互相关图Fig.9 Cross-correlation image for a point source at θ=0°, ψ=0° with poisson noise.

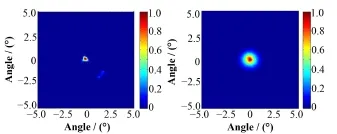
图10 含泊松噪声中心点源的重建图像左：Gauss-Seidel迭代，右：NCAR迭代Fig.10 Reconstructed images for a point source at θ=0°, ψ=0° with poisson noise. Left: Gauss-Seidel, Right: NCAR

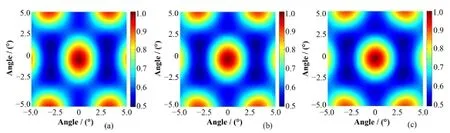
图11 含泊松噪声情况两个点源的互相关图间隔：(a) 1°，(b) 0.8°，(c) 0.6°Fig.11 Cross-correlation images for two point sources with poisson noise using NCAR algorithm. Separation: (a) 1°, (b) 0.8°, (c) 0.6°

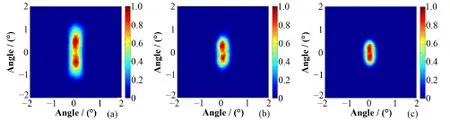
图12 含泊松噪声情况两个点源的重建图像间隔：(a) 1°，(b) 0.8°，(c) 0.6°Fig.12 Reconstructed images for two point sources with poisson noise using NCAR algorithm. Separation: (a) 1°, (b) 0.8°, (c) 0.6°

在点源间隔1°的情况下，还用Gauss-Seidel迭代进行了重建，得到的图像如图13所示。图中出现了明显的伪像，证明代数迭代方法的局部噪声放大效果。

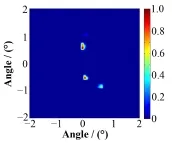
图13 Gauss-Seidel重建图像Fig.13 Reconstructed image for two point sources with poisson noise using Gauss-Seidel algorithm.

4 装置设计

仿真实现了RM成像的调制传递函数的计算，并验证了图像重建算法，在此基础上，提出了一种原理性装置的设计方案。由于采用多个探测器，且探测器直径较大导致必须有较大的像距来满足角度分辨率要求，因此RM技术不适合研制便携式仪器。本设计面向小型车辆或机器人等移动平台，平衡考虑了装置尺寸、重量和角度分辨率等指标间的关系。

RM成像装置的探测器选用12个Φ40mm×40mm的NaI(Tl)探测器，探测器排列如图14所示，探测器分为三层，中心有一个探测器，中间层间隔60°分布6个探测器，外层间隔60°分布6个探测器，相邻三个探测器构成一个等边三角形，三角形边长66 mm。

图14 RM装置探测器排列Fig.14 Detector array for prototype design.

准直器材料为铅，厚度10 mm，对662 keV γ射线的衰减约为69%，栅条状的铅由不锈钢壳包裹。准直器包含10个栅条，栅条宽度和栅条间隔都为40 mm。准直器旋转中心位于非栅条区域，这样可以减少一条铅条，减轻准直器重量。根据式(1)，装置像距设为60-100 cm可调，计算出理论视场角约为13.8°-22.3°，几何角度分辨率约为3.8°-2.3°，如果按照3.5倍超分辨，则可以达到约1.1°-0.66°的角度分辨率。

5 结语

RM成像技术采用旋转准直器和多个非位置灵敏探测器，能够在系统复杂度增加不多的情况下，扩展探测器数量，从而提高整个系统探测器面积和灵敏度。这使得RM成像系统更容易探测弱源，或者在更远距离进行成像探测。受探测器直径相对较大的影响，RM技术必须采用更大的像距来满足角度分辨率要求，因此RM技术不适合便携式仪器。但在研制基于车辆或机器人平台的大面积成像系统时，相对于CA技术，RM技术可以简化系统复杂度。由于RM技术采用了时间调制方式，因此其原始输出数据属于时间域，为了重建目标图像，需要采用互相关法将数据从时间域转换到图像空间。相对CA成像技术，RM成像技术的图像重建方法更加复杂，因此图像重建的加速算法值得研究，如通过分组迭代、直接解调等方法加快收敛速度。RM图像重建的NCAR方法可以有效抑制迭代中产生的局部噪声放大，避免伪像出现，但NCAR方法迭代次数较多，点源图像周围出现随机边缘，这是NCAR方法的缺点。在本文所做的仿真工作中，用NCAR方法能够分辨间隔0.8°的两个点源。我们也正在寻找一种可以替代NCAR的方法，以期在抑制伪像的同时，克服NCAR的缺点，进一步提高迭代重建图像的超分辨能力。

设计的RM成像装置正在建造当中，RM成像装置的实验研究正是即将开展的工作。研究结果将对仿真工作进行验证。作为一种新的γ射线成像技术，RM技术在核辐射监测领域的应用值得关注。本文对RM技术的仿真工作，实现了调制传递函数计算和图像重建。在下一步工作中，将进一步深入研究，包括给出更加精细的调制传递函数模型，本底扣除，时间域数据去噪和图像去噪等。

1 IAEA. IAEA Illicit Trafficking Database (ITDB)[R/OL]. http://www-ns.iaea.org/downloads/security/itdb-fact-sheet .pdf, 2011

2 NNSA. 国家核安全局2009年年报[R/OL]. http://haq.mep.gov.cn/pv_obj_cache/pv_obj_id_7900F2C B0E70E0D99E629309AFD40FB0B59C2701/filename/P0 20110104449064484726.pdf

NNSA annual report 2009[R/OL]. http://haq.mep.gov.cn/ pv_obj_cache/pv_obj_id_7900F2CB0E70E0D99E629309 AFD40FB0B59C2701/filename/P0201101044490644847 26.pdf

3 Ziock K P, Hailey C J, Gosnell T B, et al. A gamma-ray imager for arms control[J]. IEEE Transactions on Nuclear Science, 1992, 39(4): 1046-1050

4 Durouchoux P, Hudson H, Hurford G, et al. Gamma-ray imaging with a rotating modulator[J]. Astronomy and Astrophysics, 1983, 120(1): 150-155

5 Budden B, Case G L, Cherry M L. Image reconstruction with a LaBr3-based rotational modulator[J]. Nuclear Instruments and Methods in Physics Research A, 2011, 652(1): 610-614

6 Chen Y, Li T P, Wu M. Direct demodulation technique for rotating modulation collimator imaging[J]. Astronomy and Astrophysics Supplement Series, 1998, 128(2): 363-368

7 Budden B, Case G L, Cherry M L. Noise-compensating algebraic reconstruction for a rotating modulation gamma-ray imager[J]. IEEE Transactions on Nuclear Science, arXiv: 1003.5223v2, last revised 12 Oct 2010

CLCTL812

Study on rotating modulator imaging technique

WEI Xing WANG Feng XIAO Wuyun AI Xianyun ZHANG Bin ZHANG Lei MA Xinhua
(Research Institution of Chemical Defense, State Key Laboratory of NBC Protection for Civilian, Beijing 102205, China)

Background: Nuclear security and safety is becoming one of the most concerned topics around the world after Fukushima nuclear accident. Recent reports of IAEAshow that the potential risks exist internationally and domestically. A good solution of promoting nuclear security and safety is to develop advanced nuclear radiation monitoring technologies including γ-ray imaging. Purpose: In order to improve the sensitivity of a γ-ray imaging system with little increase of system complexity and cost, rotating modulator (RM) imaging technique using non-position-sensitive detectors was first introduced in nuclear monitoring studies. Methods: Modulation pattern of RM system was deduced mathematically and its profile was calculated by a dedicated program written in Matlab. The system sensitivity was analyzed based on the profile. Detector outputs were produced by Monte Carlo simulation. The Noise-Compensating Algebraic Reconstruction (NCAR) algorithm was applied to the image reconstruct from simulated outputs. Results: A RM imaging system has a relative sensitivity of 62% compared with a coded aperture system when detector areas of the two systems are equal. On condition that the detector diameter is 3.8 cm and image distance is 80 cm, an angular resolution of 0.8° is achieved. Conclusion: Based on the simulating results, a RM system design suitable for vehicle and robotic platform is proposed.

γ-ray imaging, Rotating modulator, System sensitivity, Image reconstruction, Iteration method

TL812

10.11889/j.0253-3219.2014.hjs.37.020401

魏星，男，1981年出生，2006年于北京防化研究院获硕士学位，现为在读博士研究生，核辐射监测技术

2013-11-05，

2013-12-13