分层均匀假设求解源非均匀分布技术

张连平 吴伦强 党晓军 韦孟伏

（中国工程物理研究院 绵阳 621900）

分层均匀假设求解源非均匀分布技术

张连平 吴伦强 党晓军 韦孟伏

（中国工程物理研究院 绵阳 621900）

定量分析放射性废物中的核素残留量可为放射性废物的分类、处理处置提供主要依据。本文采用分层均匀假设求解放射性核素分布权重的方法解决了废物样品中放射性核素的非均匀分布问题，为γ能谱法定量分析放射性废物中核素残留量时的源峰探测效率计算提供了重要技术支撑。研究表明，通过两次测量、求解矩阵方程非负解获取样品中核素的大致分布是可行的。

放射性废物，残留量，分层均匀假设

核设施运行过程中会产生大量的放射性废物。定量分析放射性废物中放射性核素的残留量，对于核材料的回收利用，放射性废物分类、处理处置等方面具有重要作用。

从核设施生产运行过程中产生的放射性废物通常大小不一，分布杂乱，且废物中放射性核素的分布很不均匀，取样化学分析时无法解决取样代表性的问题，同时放射性废物样品通常具有强的放射性和化学毒性，取样时需要进行特殊的防护，化学分析难度很大。采用无损整体测量的方式可评估整件放射性废物中总的放射性核素残留量，但同样需要采取一定的方式减小核素非均匀分布对测定结果的影响。本文拟对被测放射性废物样品采取不同方位两次测量，利用测量的不同能量多条特征γ射线强度信息，通过求解矩阵方程解的形式得到放射性核素在样品中的大致分布，从而大大减小样品中核素分布不均匀对源峰探测效率计算的影响，实现γ谱无损评估样品中放射性核素残留量的目的。

1 基本原理

1.1 源峰探测效率

在γ能谱中，被测核素的质量(m)与放射性核素的特征γ射线特征峰的净计数率(n0)的关系可表示为：

式中，M为核素的原子量；NA为阿伏加德罗常数；P为特征γ光子的分支比；λ为衰变常数；C为核素同位素的丰度值；εsp为被测核素特征γ射线的源峰探测效率。

当用γ谱分析测定放射性废物中核素总量时，源峰探测效率εsp的获取有两种定量分析方法：有标比较分析和无标理论计算。有标比较分析要求被分析对象与标准之间在物理量和几何量等方面基本保持一致，在放射性废物样品分析中这点是不可能满足的。故只能采用Monte Carlo (MC)模拟γ光子输运过程方法得到源峰探测效率值εsp。然而影响εsp计算的因素较多，尤其是废物基体吸收和源分布的影响[1]。样品中核素的非均匀分布是εsp计算的一个重要难点，本文提出分层均匀假设法的思路，对被测放射性废物样品采取不同方位两次测量，利用测量的不同能量多条特征γ射线强度信息，通过求解矩阵方程解的形式得到放射性核素在样品中的大致分布，来解决εsp计算中核素的非均匀分布难题。

1.2 分层均匀假设

γ测量放射性废物中核素总量时，γ特征峰的源峰探测效率主要随探测距离、样品层对出射γ射线的吸收等条件变化。如果探测器正对的样品深度方向上尺度适当，以切片的方式将被测样品分层考虑，对每一薄层样品中各点出射的粒子而言，探测距离、样品吸收层厚度差别很小，同一层中各点的核素粒子对探测效率的贡献基本一致。假定每层中放射性核素含量服从均匀分布，即可用MC方法方便地计算出该层核素辐射的特征γ射线对探测器探测到的光电峰的贡献[2]，层与层之间核素分布不均匀，为每层的放射性核素含量设定一个质量权重值。分层假设法的测量示意图如图1所示。

图1 分层假设时样品测量示意图Fig.1 Sketch of the layered hypothesis.

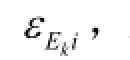
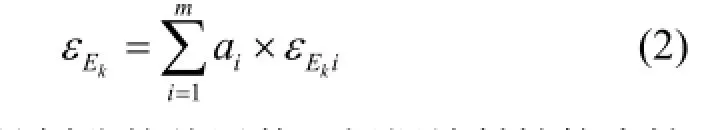
式中，m为样品划分的总层数。根据放射性核素性质选取来自同一核素的多条γ射线，这样，每选择一条γ射线，根据上面的关系式就能列出一个方程。如果所测的γ全谱中，能够找到n条方便解谱的单能射线，k=1,…,n，一次测量就可以列出n个方程，即：

方程组中，只需要设定一种能量γ射线的总源峰探测效率值jEε为未知数，因为选定的特征γ射线来源于同一核素，由式(1)可知，其余的kEε(k=1, …, n；k≠j)值可以根据测量到的不同能量γ全能峰计数率的比值乘以一个已知的系数(分支比不同引起)计算得到，即kEε=εE·jEε，常数ck=(nk·pj)/(nj·pk)，所以方程组中未知数的个数为m+1。方程组(3)变为方程组(4)的形式。

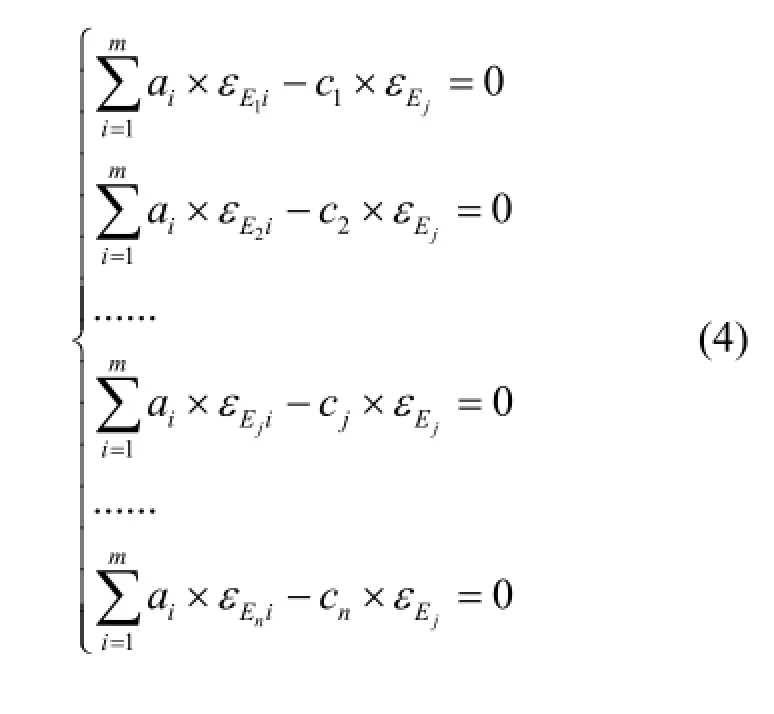
再在不同方位增加一次测量，由于两次测量的是同一对象，两次测量时式(1)中的核素质量m相等，对同一能量射线而言，测量计数率正比于测量条件下总的源峰探测效率，第二次测量时的效率参数εE'等于前次测量时的效率εE乘以两次测量得到的计数率比值n'/n，即εE'/εE=nE'/nE。这样，两次测量后总的未知数个数仍为m+1，加上所有层上权重值ai满足的归一化条件：

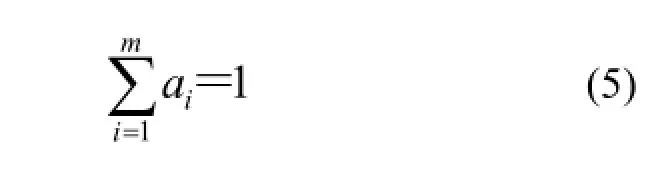
由式(4)、(5)，总共可列出的方程个数为2n+1个，未知向量为X=[a1, a2, …, am,jEε]'，共m+1个未知数，这样，可将样品划分的最大层数m等于2n。

根据上面思路建立起矩阵方程组后，利用数学方法求解矩阵方程组的非负解就可得到被测样品中各层核素的权重分布，进而可求出某条γ特征线总的源峰探测效率，根据式(1)求出样品中核素总量。

2 分层均匀假设方法求解源非均匀分布

2.1 特征能量选取

分层均匀假设方法求解源分布时利用的是同一核素的多条特征γ谱线信息，同时不同能量γ射线的强度存在较大差异，为了保证γ能峰的准确解析，需要选择单色性好、比活度较大、穿透能力较强的γ射线组合进行分析，对准确计算源分布有重要意义。

2.2 非负解求解方法

本项工作中需要求解如下数学问题的非负解：

式中，A为n×n矩阵，b为n×1的列矩阵，均为已知数据。就实际问题本身而言，尽管上面方程应该有解，但由于测量误差和其它各种因素的影响，使得数据A和b都不可避免地存在一些误差，这样就可能造成式(6)性态较差或根本无解。因而对于式(6)通常要做一些处理。最小二乘法是比较常用的一个手段，即考虑如下问题：

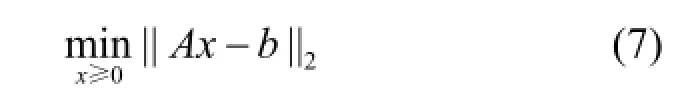
矩阵方程组解的精度很大程度上依赖于系数矩阵的特征，系数矩阵的微小扰动能引起解的巨大偏差的方程称为病态方程，病态线性方程组的判断和求解技巧如下：

计算矩阵方程解的精度可用式(8)表示(x为Ax=b的精确解)：

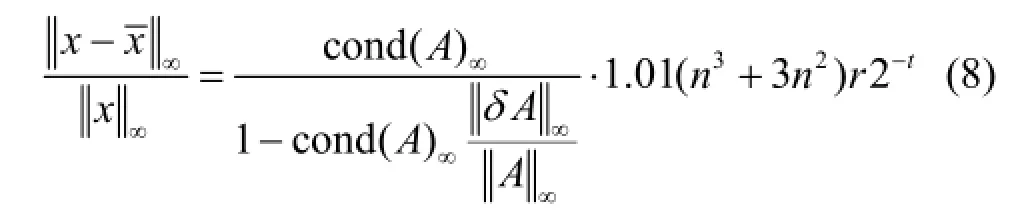
式(8)表明，计算线性方程组解的精度依赖于系数矩阵的条件数cond(A)，元素的增长因子，方程组阶数n，计算机字长t。对一般矩阵引进选主元素技巧的根本作用是为了对增长因子进行控制。完全选主元素及列主元素方法都是数值稳定的算法(即对舍入误差的增长得以控制的算法)。

条件数远大于1的矩阵称为病态矩阵，病态系数矩阵或者常数项向量的微小扰动或计算舍入误差会对求解结果带来很大变化，这样的方程组称为病态方程组。用选主元素的消去法不能解决病态问题，对于病态方程组可采用高精度的算术运算(采用双倍字长进行运算)或者采用预处理方法，即将矩阵方程Ax=b转化为一等价方程组然后求解。常用的预处理方法是将系数矩阵中的元素进行统一的缩放，减小矩阵元素与列向量b中元素数量级上的差异，这样处理后可大幅减小矩阵条件数[3]。

实际测量过程中，由于测量统计误差和γ能谱各特征能峰解谱误差无法消除，采用分层均匀假设方法建立的系数矩阵病态性往往比较严重，求解结果不能真实反映核素在样品中的实际分布。加上对上述矩阵方程组而言，非负解才是具有物理意义的解，只有在保证矩阵方程病态性不严重的情况下求解得到的核素分布结果才可用于实际测量条件下的探测效率计算。实际应用中，用求解矩阵方程组得到的各层样品中的源权重值进行插值获得源在整个样品中的分布，根据这个源分布计算几个不同能量特征γ射线的源峰探测效率，与实际测量值比较，根据实际测量的不同能量特征γ射线的相对强度情况作为判断计算得到的源分布是否接近真实分布的依据。

Matlab库函数中提供了一个求解矩阵方程组非负解的函数lsqnonneg ()，函数说明如下：

函数调用形式为：

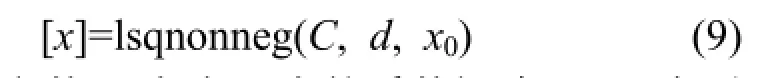
式中，输入参数C为式(4)中的系数矩阵A，d为列向量b，C、d必须为实数；可选项x0为迭代初始点(x0所有元素需大于0)，当x0为空或者只有两个输入参数时，使用x0的缺省值，缺省值为原点。

3 结果与讨论

将U3O8标准物质分装成27个小样品，采用点阵排布的方式放置在1000 mm×800 mm×500 mm的支架上组成空间非均匀分布的样品源。用高纯锗γ谱仪在样品的前、后、左、右方位分别进行测量，测量结果见表1。

表1 实验验证样品不同方位的测量结果Table1 Measurement results of validating samples from different orientations.

235U有143.76 keV、163.33 keV、185.72 keV、205.31 keV特征γ射线。选择上述γ射线，在不同方位两次测量时，可将样品划分为8层，设定8个权重值，求解9次线性方程组进行计算处理。

形成式(4)方程组时，系数矩阵中层内均匀假设下的各层分效率值jEiε用经验证的自编MC效率计算程序[4]计算得到。实验条件下计算得到的源峰探测效率约为10-5量级，比归一化条件方程中ai的系数值1小很多，所以最后组成的系数矩阵可能为一个病态矩阵，求逆过程中的舍入误差会给计算结果带来很大的影响，将方程两端同乘以104，可有效减小矩阵的病态性。

以左、右面的测量数据为依据，将样品箱分割成8层，每一层的探测距离分别为125 cm、133.6cm、142.1 cm、150.7 cm、159.3 cm、167.9 cm、176.4 cm和185 cm，各层上核素的权重设为a1-a8，假设左、右面测量时，185 keV射线的总绝对探测效率为ε185L、ε185R，ε185L是未知数，ε185L/ε185R= n185L/n185R。ε143L/ε185R=(n143L/n185L)·(p185/p143)，由测量数据得到，其中p185为能量为185 keV γ射线的能量分支比。共9个未知数，列9个线性方程。计算两组系数矩阵下求解矩阵方程非负解，得到左右面测量时各层权重值，计算得到185 keV γ射线的总探测效率值ε185L、ε185R，从而可求出被测核素235U的质量。

构建参照样品时，将U3O8粉末样品装入27个直径为24 mm的小玻璃瓶内，铀核素的几条特征γ射线能量均较低，U3O8粉末样品的自吸收和玻璃瓶对特征射线的吸收对各层分效率的计算有显著影响。计算吸收矩阵时，在不考虑参照源样品自吸收的条件下计算得到分效率值的基础上，同乘以特征γ射线在一个小玻璃瓶中的等效穿透系数，作为U3O8粉末样品的自吸收和玻璃瓶对特征射线的吸收的校正。这种处理无法考虑特征γ射线路径上其他样品瓶的吸收，所以计算效率值偏大，得到的核素质量值会偏低。系数矩阵及对应结果见表2。

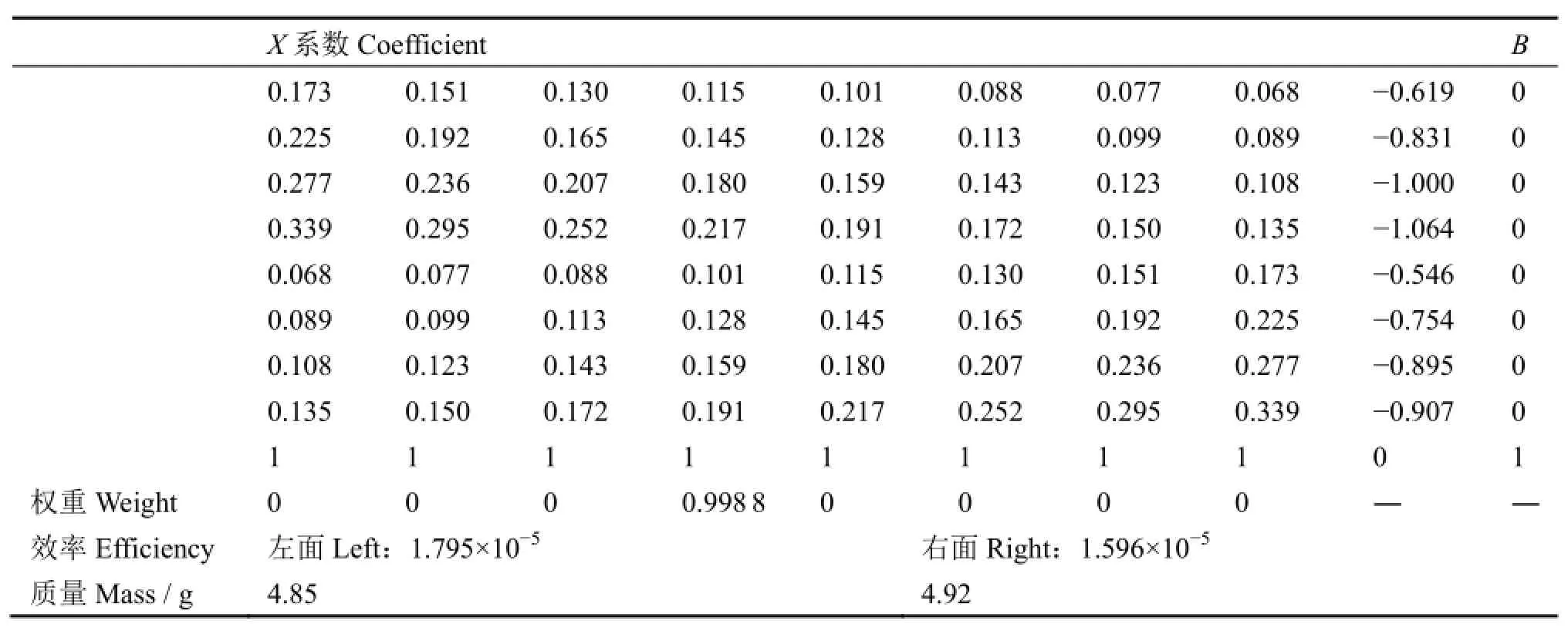
表2 左、右两次测量时系数矩阵及计算结果Table2 Coefficient matrixes and results from the left and right.

同样，以前、后面的测量数据为依据，将样品箱分割成8层，各层上核素的权重设为a1-a8，假设185 keV射线的绝对探测效率为ε185F，是一个未知数，ε185F/ε185B=n185F/n185B。ε143F/ε185F=(n143F/n185F)× (p185/p143)，由测量数据得到。共9个未知数，列9个线性方程，系数矩阵及对应结果见表3。

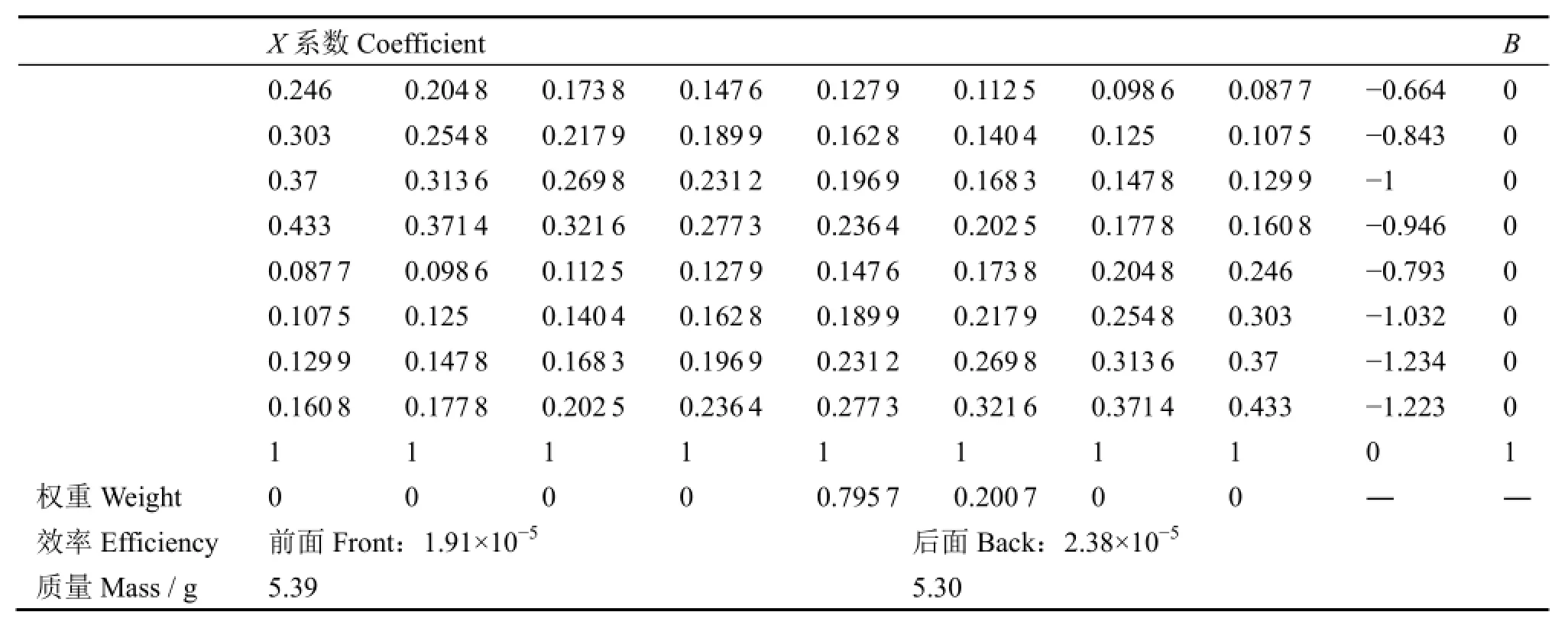
表3 前、后两次测量时系数矩阵及计算结果Table3 Coefficient matrixes and results from the front and back.

从表3和表4的计算结果看出，以左、右面的测量数据和以前、后面的测量数据为依据计算得到的235U质量值比较接近，但均与标称值7.256 g相差较大，分析偏差较大的主要原因如下：

(1)235U可供选择的几条特征γ射线能量低，介质吸收作用强，介质吸收作用对测量结果有较大的影响，由此引起的系统偏差较大。

(2)235U可供选择的几条特征射线能量间隔很小，不同能量射线携带的核素在源中分布的信息较弱，不如钚同位素特征射线的明显，利用235U的几条不同能量特征γ射线信息求解源中核素分布会带来较大偏差。

由于放射性废物中填充物的大小不一、分布散乱，空隙率未知，γ无损分析放射性废物样品中的核素残留量的不确定度主要源于源中核素的未知分布和计算样品介质质量吸收系数时介质实际密度的不确定性。为了将待测的放射性废物样品中的核素残留量测量结果评估的不确定度控制在一个可接受的范围内，γ测量前应对待测的放射性废物样品做适当的前处理，通过将样品分装成若干小尺寸样品来减小测量样品的尺寸，从而减小源分布对测量结果的影响；尽量将样品夯实以减小样品的空隙率，从而可减小样品介质吸收计算时引入的不确定度。

4 结语

基于分层均匀假设，利用不同能量多条特征γ射线强度信息，构建矩阵方程组求解了放射性核素在样品中的分布权重，有效减少了样品内核素未知非均匀分布对源峰探测效率计算时的不确定性。构建铀参照样品，通过不同方位的两次测量、求解矩阵方程非负解获得了样品中核素的大致分布，但由于235U可选特征线能量间隔很小，计算得到的235U质量值与标称值相差较大，其计算结果可能还需要进一步验证。

1 Vargas M J, Timon A F, Diaz N C. Monte Carlo simulation of the self-absorption corrections for natural samples in gamma-ray spectrometry[J]. Applied Radiation and Isotopes, 2002, 57(6): 893-898

2 Ewa I O B, Bodizs D, Czifrus Sz, et al. Monte Carlo determination of full energy peak efficiency for a HPGe detector[J]. Applied Radiation and Isotopes, 2001, 55(1): 103-108

3 孙苏亚, 杨兴东, 张佳静, 等. 一类线性方程组解的条件数估计[J]. 南京信息工程大学学报(自然科学版), 2011, 3(2): 190-192

SUN Suya, YANG Xingdong, ZHANG Jiajing, et al. The condition number estimation for a class of linear systems[J]. Journal of Nanjing University of Information Science & Technology, 2011, 3(2): 190-192

4 韦孟伏, 张连平, 蒋国强, 等. γ辐射场探测特征γ全能峰绝对探测效率的Monte Carlo计算[J]. 核技术, 2004, 27(5): 344-349

WEI Mengfu, ZHANG Lianping, JIANG Guoqiang, et al. Monte Carlo simulation of absolute efficiencies of coaxial HPGe detector for known source distribution[J]. Nuclear Techniques, 2004, 27(5): 344-349

CLCTL271+.99

Acquiring the nuclide distribution based on the hypothesis of layered uniform distribution

ZHANG Lianping WU Lunqiang DANG XiaoJun WEI Mengfu
(China Academy of Engineering Physics, Mianyang 621900, China)

Background: The running of the nuclear system would produce a mass of radioactive waste, and the nuclide residual in these radioactive waste had to be analyzed. Purpose: The aim is to provide a main support to solve the problem of waste classifying and disposal by the quantitative analysis of the nuclide residual in the radioactive waste by gamma-ray spectra. Methods: The nuclide distribution has been researched by solving the weighted factor in every layer based on the hypothesis of layered uniform distribution, which could provide an important support for the calculation of detecting efficiency. Results: The weighted factor in every layer was calculated based on the hypothesis of layered uniform distribution. The measurement results from two different orientations, and the more accurate efficiency of source-peak were acquired. Conclusion: The results show that it is feasible to acquire the nuclide distribution by two-time measurement and solving the non-negative result of the matrix equation.

Radioactive waste, Residual, Hypothesis of layered uniform distribution

TL271+.99

10.11889/j.0253-3219.2014.hjs.37.020602

张连平，男，1975年出生，2006年于中国工程物理研究院获硕士学位，副研究员，从事核技术应用研究工作

2013-10-10，

2013-11-24