于桥水库溃坝洪水演进研究

2014-02-15廉铁辉黄毅

海河水利 2014年4期

关键词：溃口溃坝洪水

廉铁辉，黄毅

（1.天津市引滦工程于桥水库管理处，天津301900；2.天津市水利科学研究院，天津300061）

于桥水库溃坝洪水演进研究

廉铁辉1，黄毅2

（1.天津市引滦工程于桥水库管理处，天津301900；2.天津市水利科学研究院，天津300061）

于桥水库作为天津市唯一一座具有防洪、城市供水、发电、灌溉等综合功能的大（1）型水库，作用和地位十分重要。开展溃坝研究编制风险图的目的是水库遭受特大洪水、强烈地震、地基地质变化等情况时，能正确预测溃口流量过程线及溃坝致灾情况，以便为避险、抢险、洪水保险等工作提供依据。针对于桥水库土坝渐溃溃口采用DAMBRK模型进行分析，针对下游平原采用二维网格离散，形成了土坝溃决洪水演进的数值模型并计算分析。

溃坝；溃口；DAMBRK模型；洪水演进；于桥水库

1 概况

于桥水库建成于1960年，是天津市最大的水库，也是引滦入津工程重要的调蓄水库。水库建成以来，为下游的防洪安全、保障供水等发挥了巨大的效益，特别是1983年引滦入津工程建成通水以来，为天津市经济社会可持续发展和社会稳定作出了重要贡献。于桥水库防洪标准为千年一遇设计、可能最大洪水校核，总库容15.59亿m3，控制流域面积2 060 km2，正常蓄水位21.16 m（大沽高程，下同），正常蓄水面积86.8 km2，平均蓄水水深4.6 m。大坝为均质土坝，坝顶长2 215 m（主坝桩号0+000-1+935，副坝桩号-0+280-0+000），最大坝高24 m，最大泄洪能力4 138 m3/s。水库遭遇超标准洪水，溢洪道闸门无法开启并且主坝坝体存在重大险情时，应急措施是将副坝桩号0+000以南凹形山口段炸开，宣泄洪水。

2 溃口模型

一般情况下，导致土坝溃决的原因有两类，即漫溢和管涌，其中以坝顶漫溢较为常见。破坏程度取决于溃坝流量和持续时间，即溃口流量过程。管涌破坏历时最短，但溃口形成的最终形状同漫溢一样。坝体溃决的形式有渐溃和瞬溃两类，土坝溃决大多是渐溃形式，其洪水过程线较长，起涨段可达十几分钟至数小时，退水过程较慢。

选用DAMBRK模型计算于桥水库由于漫溢原因造成的渐溃情况。DAMBRK模型是美国国家气象局的溃坝洪水预报模型，由弗雷德（Fread）在1988年开发研制。溃口形状由溃决历时、溃口最终底宽、溃口底部高程和溃口边坡4个输入参数确定。模型假定溃口底部从1个点开始，在整个历时内其宽度以线性速率增长，一直到溃口最终宽度；同时，溃口的底部高程也不断发展，直到最终位置。根据流体力学理论计算坝址泄水过程和向下游河道的演进。溃口洪水由宽顶堰流公式计算，考虑行进流速及下游水位对堰流可能产生的淹没影响，并以一维非恒定流方程组的隐式有限差分解计算溃坝洪水向下游的演进。选用土坝瞬溃中普遍使用的宽顶堰流公式，计算由于炸副坝原因造成的瞬溃情况流量过程。

2.1 渐溃溃口流量过程

于桥水库控制流域面积较小，因此渐溃方式下不再考虑上游来水量。于桥水库大坝渐溃发生在洪水溢出坝顶后，漫溢洪水对坝体冲刷后逐渐形成溃口且逐渐扩大[1]，导致渐溃险情。水库下泄流量由两部分组成，一是通过溃口的下泄流量（Qb），二是通过泄水建筑物的下泄流量（Qs），其计算公式为：

渐溃溃口为梯形时，堰流计算公式如下：

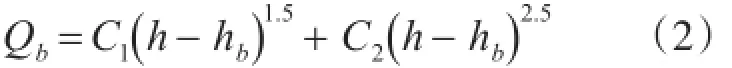
其中：

Cv的计算公式为：

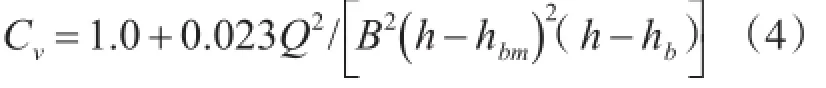
其中：

式中：Q为水库总下泄流量（m3/s）；h为漫顶溃坝时的水位（m）；hb为瞬时溃口底部高程（m）；bi为瞬时溃口底宽（m）；Cv为行进流速修正系数；Ks为堰流受尾水影响的淹没修正系数；Z为坡度；B为坝址处的水库水面宽度（m）；hbm为终极溃口底高程（m）；ht为尾水位（靠近坝下游的水位）（m）；hd为坝前水深（m）；tb为溃口形成时间（h）；τ为溃口形成历时（h）；b为终极溃口底宽（m）。

尾水位（ht）可由曼宁公式推算得到：

式中：n为曼宁糙率系数；S为坡降；A为过流断面面积（m2）；B为过流断面的水面宽（m）。

溢洪道下泄流量（Qs），按照给定的溢洪道泄量曲线拟合成如下公式，根据不同的水位（h）计算。

经过计算，最终溃口形状为梯形，底宽300 m，高24 m，坡比为1.47，溃口形成历时为2 h。水库在渐溃开始后22 h停止下泄洪水，总下泄水量约15亿m3，如图1-2所示。

2.2 瞬溃溃口流量过程

于桥水库大坝炸副坝方案中，副坝最大坝高3.5 m，其下是稳固地质，所以溃口深度取3.5 m，溃口长度为副坝长280 m。瞬溃溃口形状可近似为矩形，堰流计算公式如下：

式中：σ为沉溺系数（淹没系数），取σ=1；m为宽顶堰流量系数，取m=0.36；ε为侧向收缩系数，取，其中hd是堰高（m）、H0是坝前水深（m）、b为溃口长度（m）、B为坝址水面宽度（m）。

图1 渐溃流量变化

图2 渐溃水位变化

假设在水位达到27.72 m时，于桥水库采取炸副坝的措施，经计算瞬溃瞬间溃口最大流量为2 777 m3/s，其后的溃口流量采用宽顶堰流量公式计算，在溃坝约50 h后停止下泄，总下泄水量约为7亿m3，如图3-4所示。

图3 瞬溃流量变化

图4 瞬溃水位变化

3 下游平原洪水演进模型

3.1 数学模型

由于坝址下游紧邻蓟县山前平原地区，这种情况下，一维模型计算结果准确性较低，适宜采用二维网格模型计算洪水演进情况，因此实际计算中不采用DAMBRK模型中计算下游洪水演进的部分。

由于计算中要考虑溃坝洪水漫过州河、泃河、蓟运河大堤的情况，所以采用水力学一、二维模型耦合的方法计算下游洪水演进。其中，一维模型用于计算州河、泃河、蓟运河河道内洪水的演进，二维模型用于计算溃坝洪水在平原地区的演进，两者耦合可以计算一维河道内的洪水是否溢出到平原二维网格中，或二维网格中的洪水是否流进河道中。

一维非恒定流基本方程包括水流连续性方程和水流运动方程。

水流连续性方程为：

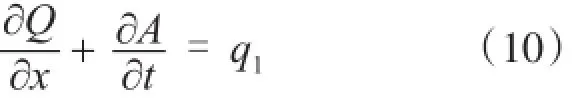
水流运动方程为：

式中：Q为流量（m3/s）；x为沿程距离（m）；A为过水断面面积（m2）；t为时间（s）；q1为侧向单位长度注入流量（m2/s）；β为动能修正系数；g为重力加速度（m/s2）；Z为水位（m）；n为糙率系数；R为断面水力半径（m）。采用有限体积法处理一维模型，并用迎风格式处理其中的对流项。

二维非恒定流基本方程包括水流连续性方程和水流运动方程。

水流连续性方程为：

水流运动方程为：

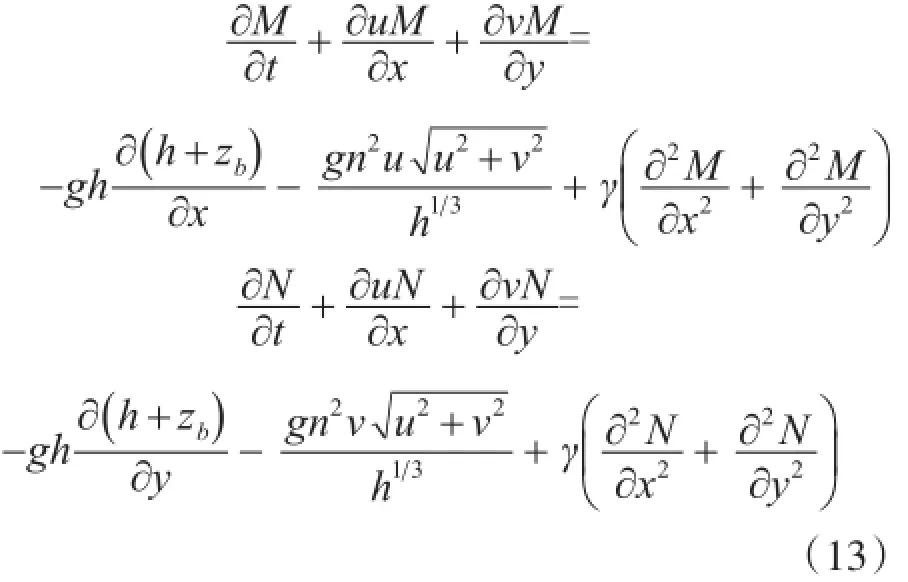
式中：Z为水位（m）；M=uh；N=vh；h为水深（m）；zb为河床高程（m）；u和v分别为x和y方向的流速（m/s）；γ为紊动黏性系数。方程离散时空间上采用有限体积法，运用守恒格式对水流连续性方程进行离散，保证计算域内水量守恒；时间上采用蛙跳法，使用交错网格计算物理量的分布。

3.2 网格划分

在下游洪水演进计算中，网格划分是至关重要的。下游计算涉及蓟县、宝坻、宁河3个区县。研究对象包括：研究范围内的主要河流及其堤防，主要蓄滞洪区，与此项目相关的闸门，主要铁路及高速公路等。其中，河流包括州河、泃河、蓟运河、鲍邱河；蓄滞洪区包括青甸洼、太和洼、黄庄洼、盛庄洼；闸门包括南周庄闸、邵庄子闸、东赵闸；公路铁路包括津蓟高速公路、京沈高速公路、大秦铁路、京秦铁路、津蓟铁路。如何将这些有阻水作用的建筑物嵌入DEM地形中是网格划分的关键点。

首先，利用现有2010年的天津市1∶10 000电子地图提取出地形高程点及研究对象的坐标（包括堤防、闸门、高速公路、铁路）。其次，由于研究对象的高程在现有2010年天津市1∶10 000电子地图中资料不全，还需要收集研究对象的高程。涉及高速公路包括津蓟高速公路、京沈高速公路，采用实地查勘的方式得到每个查勘点在高速公路上的相对位置及每个查勘点对于地面的相对高度。最后，将实地查勘资料转化到电子地图中，在计算范围内（3 430 km2）共生成267 869个非结构网格。其中，在堤防、高速公路、铁路处加密。网格精度可达到50×50 m2级别。网格最大面积为60 000 m2，为200 m×300 m，精细度足够描述下游地形。在河道、高速公路、铁路的区域采用嵌套区域的技术加密网格，面积为50 m×50 m，以准确描述实际地形。

下游平原糙率为0.08；河道主槽糙率为0.022 5，滩地糙率为0.037；计算时间为15 d。