具有Allee 效应的广义Logistic 模型的捕获优化问题

李文霞，雒志学

近年来，许多学者对单种群生长规律的生物模型进行了研究，并得到了许多有意义的结果.文献［1，2］分别研究了含Allee 效应经典的Logistic 模型的开发与优化，文献［3］研究了单种群模型的最优捕获策略.文献［4］研究了具有Allee 效应的种群的优化管理.文献［5］对Logistic 模型进行了推广，得到了广义Logistic 模型.文献［6］探讨了广义Logistic 模型

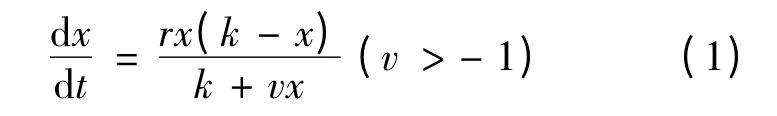
的优化开发.文献［7］中研究了具有常数捕获率的广义Logistic 模型在含Allee 效应的情况下的定量开发.

大量事实证明，许多物种被报道具有Allee效应，如植物［8］、海洋无脊椎动物［9］、哺乳动物［10］等.因此，对于很多种群，尤其是那些濒危的哺乳类动物，其种群密度稀疏，更容易受Allee效应影响.所以，考虑具有Allee 效应的种群更具有实际意义.另外，在实际问题中，人们要充分利用资源，于是对资源进行开发，而且存在过度开发现象.

本文考虑具有Allee 效应的广义Logistic 模型的线性捕获优化问题，不仅克服了文献［7］中常数捕获率的局限性，而且考虑最优捕获问题，寻求最优捕获策略，维持生态平衡，使生物资源可持续发展.

我们假设捕获与种群密度和捕获努力度成正比，即h(x)= Eqx.E 为捕获努力度，q 为捕获能力系数，为正常数，为运算方便，不妨令q=1.我们研究如下模型

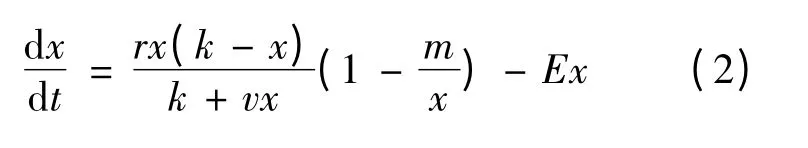
其中:r 为种群的固有增长率，k 为环境容纳量，x(t)为t 时刻的鱼群数量，v ＞－1，0 ＜m ＜k，E ＞0，r ＞0.

我们首先研究系统正平衡点的存在性及稳定性问题.

1 系统(2)正平衡点的存在性及稳定性

1)当v=0 时，系统(2)可变形为

证明:该定理易证明，故在此省略其证明.

且x=x1*不稳定，x=x2*稳定，稳定域Ω=当时，系统(3)无正平衡点.

故x1*＞0，x2*＞0，于是(3)可变形为

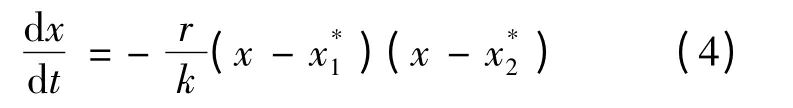
由(4)知，当0 ＜x ＜x*1时当x1*＜x ＜时，当x ＞x2*时，故x1*不稳定，x*2稳定.稳定域当E时，

故x*1＜0，x*2＜0.即系统(3)无正平衡点.

2)当v ≠0 时，系统(2)变为

令

①当－1 ＜v ＜0 时，定理证明完毕.

定理3 Ⅰ.当E=E1时，(6)有唯一的正平衡点

且x*半稳定，稳定域当E=E2时，(6)无正平衡点.

Ⅱ.当0 ＜E ＜E1时，(6)有两个正平衡点x1*，x2*，且x1*不稳定，x2*稳定，稳定域Ω=

其中:

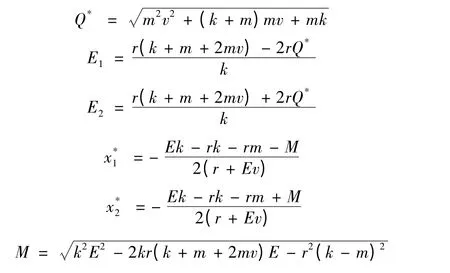
证明

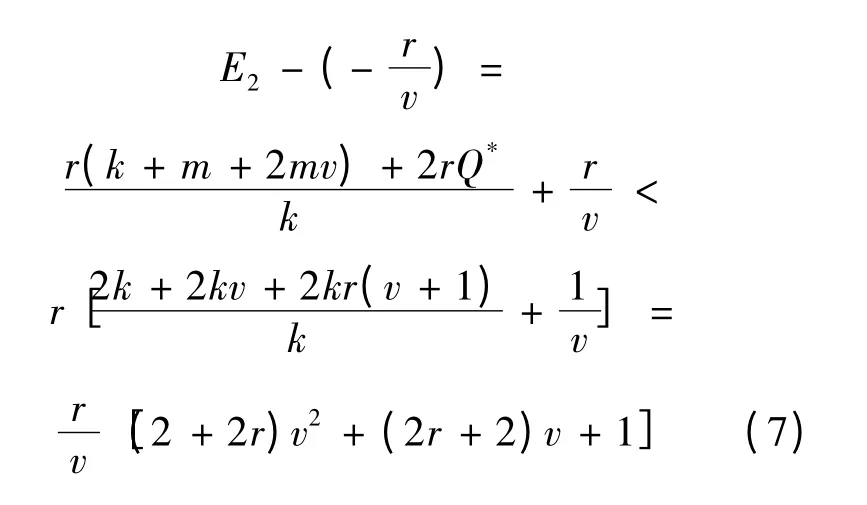
当－1 ＜v ＜0 时，(2 +2r)v2+(2 +2r)v +1 ＞0 恒成立，故(7)式小于0，即又由于E1＜E2，所以r + E1v ＞0，r + E2v ＞0.

(Ⅰ)当E=E1时，(6)有唯一的正平衡点(5)可变形为

又由于

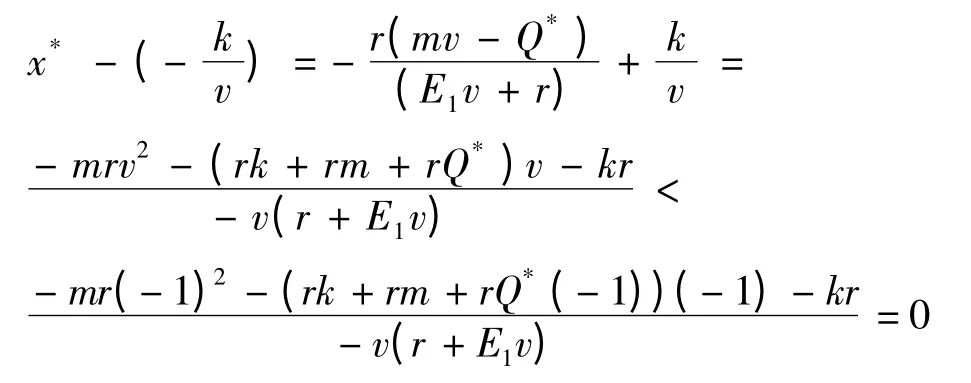
其中，Q*(－1)表示v=－ 1 时Q*的值，则x*故x*半稳定，稳定域

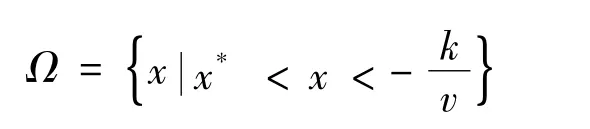
当E=E2时，，故(6)无正平衡点.

(Ⅱ)由于0 ＜E ＜E1，(6)有两个正平衡点，经比较可得可变形为

当0 ＜x ＜x*1时，当x1*＜x ＜x2*时，当时，;当x ＞时，故x1*不稳定，x2*稳定，稳定域

②当v ＞0 时，定理证明完毕.

类似定理3 的证明方法，易得下面定理

且x*半稳定，稳定域当E=E2时，(7)无正平衡点.

Ⅱ.当E ＞E2或0 ＜E ＜E1时，(6)有两个正平衡点x*1，x*2，且x*1不稳定，x*2稳定，稳定Ω(其中，E1，E2，x*1，x*2同定理3)

下面我们考虑最大可承受产量.

2 最大可承受产量

再令－vx2－2kx +k2+mk +vkm=0，解得x1=其中θ

1)当v ＞0 时，x1＜0 舍去，则

2)当－1 ＜v ＜0 时，由于mv2+ (k + m)v＜0，故x2也大于0，若取

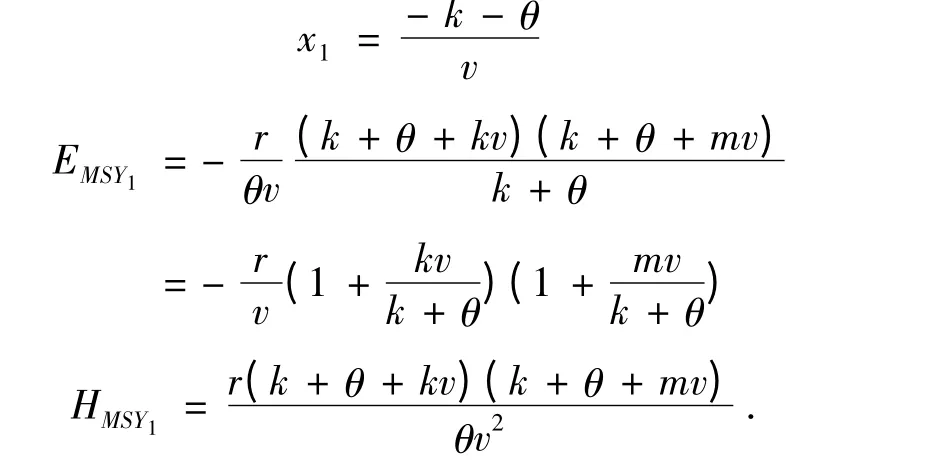
若

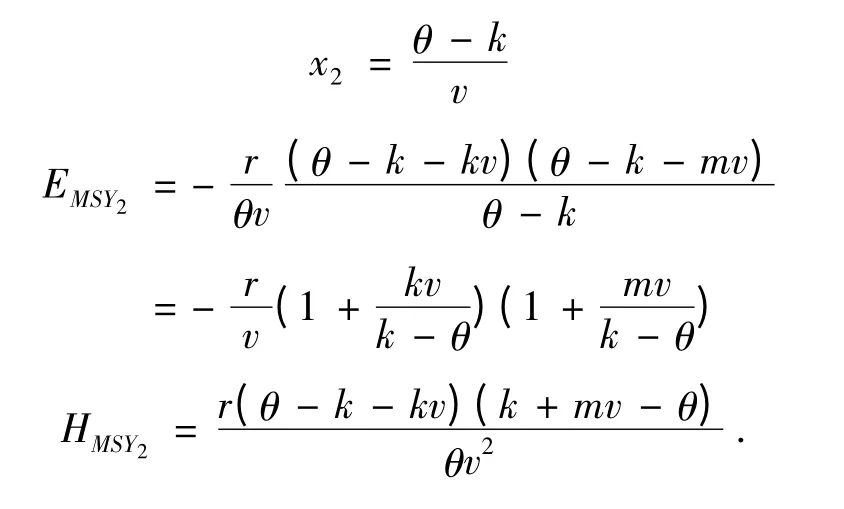
显然EMSY1＞EMSY2，HMSY1＞HMSY2，所以EMSY=EMSY1，HMSY=HMSY1.

1.1 浅层学习与“深度学习”的区别 高中生物学具有概念多、理解难，理论多、实践难的学科困境。笔者曾在高中生物学教学课堂中进行问卷调查，分析发现浅层学习在教学中还有一定的市场。较多的教师和学生将生物学当成文科看待，认为生物学凭记忆就能得高分，背诵默写成为部分课堂教学的常态。课堂上学生成为速记员和听众，被动接受知识，学习过程缺少反思，长此以往，会导致学生思维方式的僵化，学生的生物学学科素养就会低下。

令－2kx + k2+ mk=0，得故

最后我们讨论该模型的最优捕获策略.

3 最优捕获策略

在实际问题中，我们想寻求一个最优捕获强度E＊＊，从而得到一个最优平衡种群规模，使目标泛函取得最大值.这里，我们取λ(x，E，t)= PEx－aE，其中P 表示市场价格，a 表示成本价格，λ 表示单位时间内的纯收益，δ 是贴现率.那么对种群的最优捕获问题即转化为如下的最优控制问题:

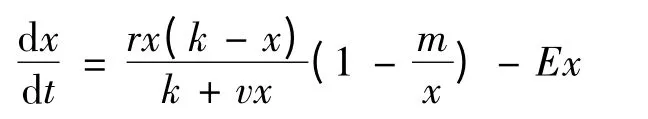
由最大值原理，作Hamilton 函数

其中，λ 为伴随变量

由于H 关于变量E 是线性的，则其最优控制为bang－bang 奇异控制.根据Pontryagins 最大值原理有:

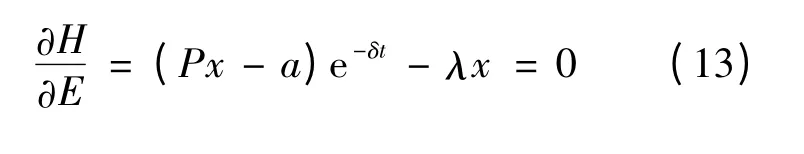
可得

由(12)式可得

由(14)式、(15)式可求出

将(16)式代入(17)式中，可得最优捕获强度:

4 结论

从本文的研究结果可以看出，在广义Logistic模型中引入Allee 效应更具有实际意义.其次，研究最优捕获问题更利于资源的保护和利用.它比较接近现实应用.

［1］ 范猛，王克，周毅.具有临界增长的生物种群的开发［J］.丹东师专学报，1999，78(4) ：3 －5.

［2］ 柴娟，雒志学.具有临界增长的生物种群的捕获优化［J］.重庆工学院学报，2008，22 (12) ：63 －66.

［3］ 鲁红英.一类自治单种群模型及其最优捕获策略［J］.系统科学与数学，2010，30 (1) ：33 －42.

［4］ 黄林林，赵立纯.基于Allee 效应的鱼种群资源管理［J］.鞍山师范学院学报，2013，15(2) ：4 －7.

［5］ 王寿松.单种群生长的Logistic 模型［J］.生物数学学报，1990，5(1) ：21 －25.

［6］ 黄辉.广义Logistic 模型的优化开发［J］.中山大学研究生学刊，1996，17(1) ：7 －14.

［7］ 夏锋.含Allee 效应的广义Logistic 模型之定量开发［J］.中山大学研究生学刊，1995，16(2) ：33 －42.

［8］ Ferdy J，Austerlitz F，Moret J，et al.Pollinator induced density dependence in deceptive［J］.Oikos.1999，87(7) ：549 －560.

［9］ Stoner A，Ray C M.Evidence for Allee effects in an over－harvested marine gastropod：density dependent mating and egg production［J］.Marine Ecology Progress Series，2000，202(3) ：297 －392.

［10］ Kuussaari M，Saccheri I，Hanski I.Allee effects and population dynamics in the glanrille fritillary butterfly［J］.Oikos，1998，82(17) ：384 －392.

［11］ 马知恩.种群生态学的数学与研究［M］.合肥：安徽教育出版社，2000.