Privalov 定理的一个推广

毕文姗，刘 华

(天津职业技术师范大学理学院，天津 300222)

Privalov 定理是几何函数理论尤其是解析函数边值问题研究方向的奠基性工作.经典的Privalov 定理［1］指对光滑简单曲线Γ 上的Hölder指数为0 ＜μ ＜1 的连续函数f(t)，其Cauchy 积分

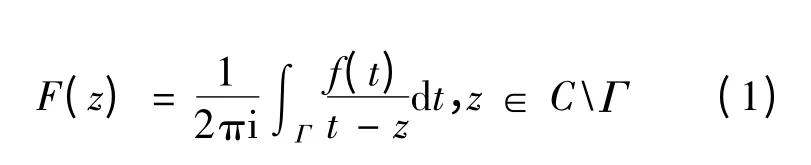
在Γ 上的正负边值F+(t)、F－(t)均存在且属于Hölder 空间Hμ(Γ).同时f(t)的奇异积分

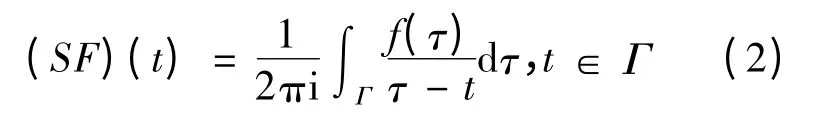
也属于Hμ(Γ)，或者换句话说，Hμ(Γ)是奇异积分算子的不变子空间.这在奇异积分方程理论的研究中是至关重要的.

现代数学和工程技术的发展，使得在研究解析函数边值问题和奇异积分方程时需要摆脱Hölder 条件的束缚.如电磁场的边界就可能很复杂［3］，即使在经典的材料力学的应用上，由于分子水平材料技术的兴起，连续的边界值理论已不够用［4］.另外，奇异积分方程的扰动理论也不可避免地要用到非连续数据［5］.

本文就针对这些应用，尝试把Privolov 理论推广到不连续情况.实际上，Privalov 定理可以推广到L2空间中［2］，但这个空间太大，在实际应用中不够精细，力学中最重要的奇性分析就得不到.因此，作者需要寻找一类合适的空间来讨论.

1 预备知识

记复平面的单位圆盘为D，其边界∂D 以逆时针为正方向，对f(t)∈Lp(∂D)，其对应的分区解析函数和奇异积分变换如(1)、(2)所示.

带权Besov 解析函数Bps空间是满足

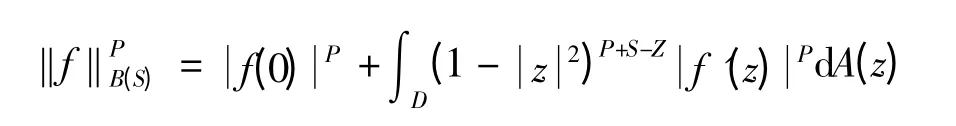
的D 上的解析函数的集合，其中1 ＜P ＜∞，0 ＜S ＜ 1.后文中用dAP，S(z)=(1－，即

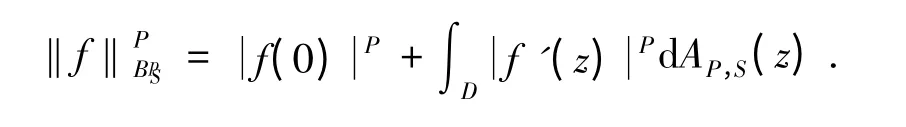
对于f(t)∈LP(∂D)，如果

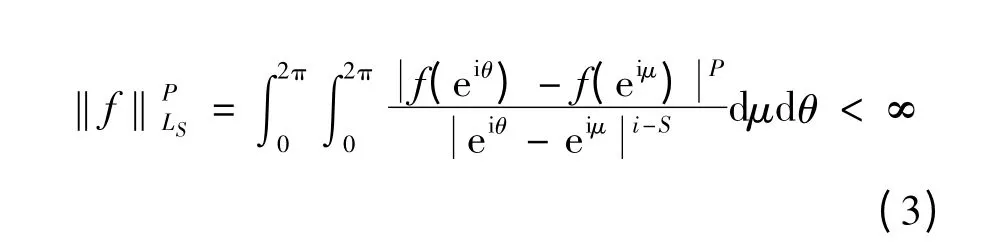
则称f ∈LP(∂D)，其范数定义为

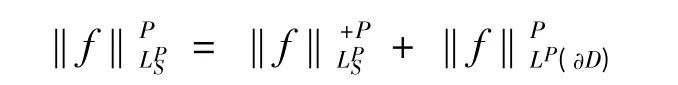
可以证明LPS(∂D)是一个Banach 空间［6］.

LPS(∂D)空间可以看作是Hölder 空间的某种完备化.实际上，设f(t )(∂D)，S' ＜S，则

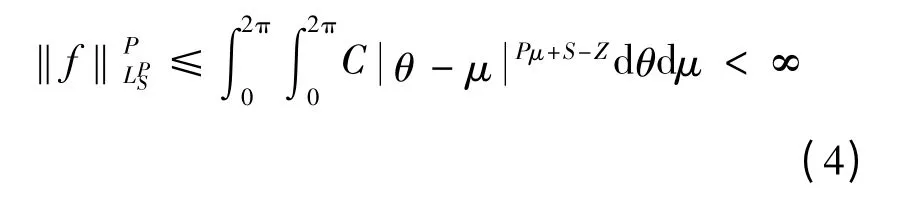
这里C 代表某个常数.这个记号在后文中用到的时候也是如此，即不同的常数都用C 表示而不作区分.

2 主要定理

先给出两个引理:

引理1 设1 ＜P ＜∞，0 ＜S ＜1，F ∈A1(D)，limF(reiθ)对eiθ∈∂D 几乎处处存在.如果，则f ∈LPS.

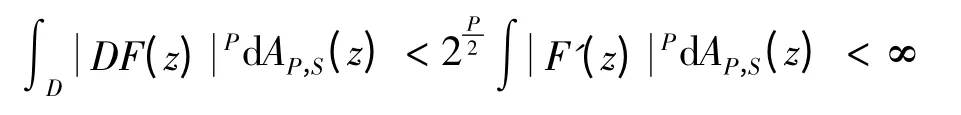
由文献［7］中的引理4.1 得证.

因为Besov 空间是Hardy 空间的子空间，所以Besov 函数在边界的极限总是存在的，故引理1 指出Besov 空间BPS中函数的边界值在空间LPS中.实际上，下面引理说明它反过来也是对的，即对任一个f ∈LP(∂D)，存在¯f ∈BPS，使得f 是¯f的非切向边值.

引理2 设1 ＜P ＜∞，0 ＜S ＜1，且f ∈LP(∂D)，f ∈LPS，则

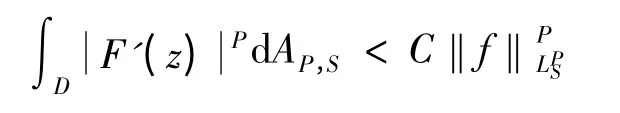
证明 设z=reiμ，则由文献［1］引理1.3.2证明(即里面的zL=eiμ)有

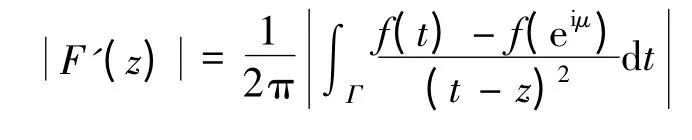
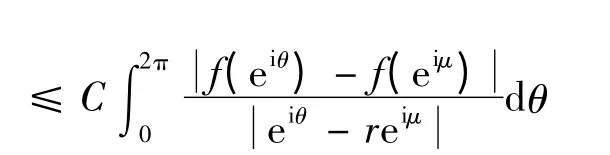
由Hölder 不等式

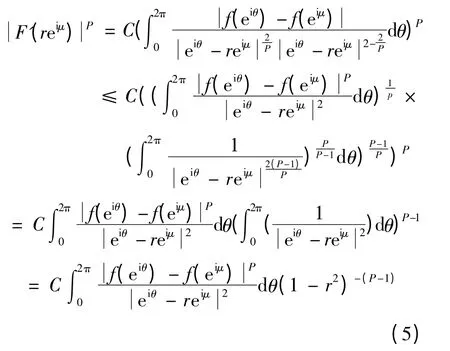
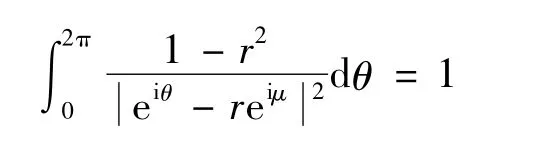
再由(5)式得

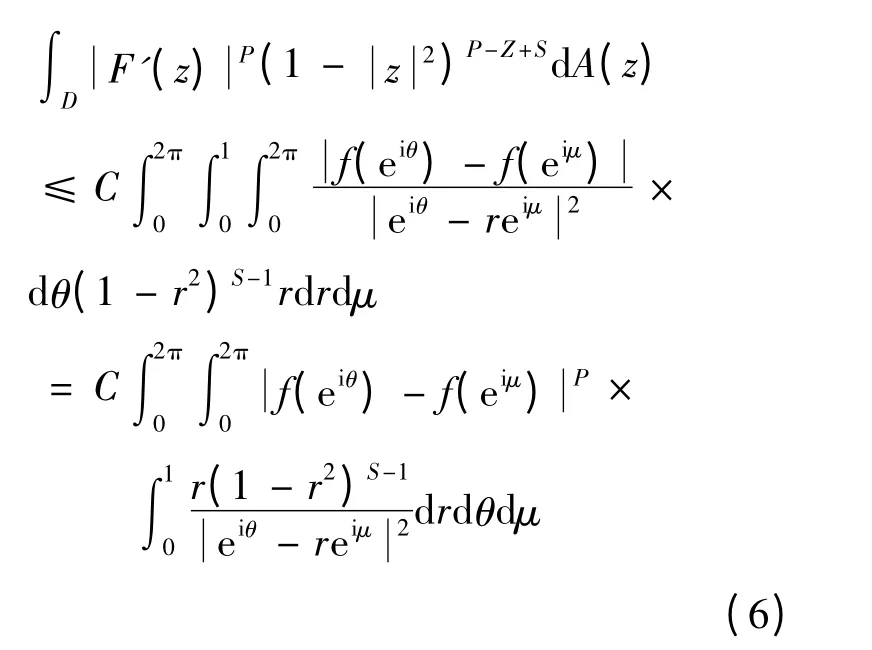
由文献［7］中(4.4)式

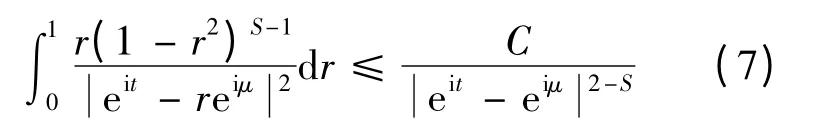
故(6)式和(7)式联合给出

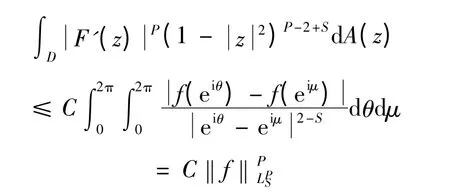
证毕.

本文的主要定理如下:

定理3 设1 ＜P ＜∞，0 ＜S ＜1，且f(t)∈LP(∂D)∩LPS(∂D)则F+(t)、F－(t)和SF(t)均在LP(∂D)∩LPS(∂D)中.

证明 由文献［2］LP情形下的Privalov 定理，F+(t)、F－(t)及 SF(t)均 属 于 空 间LP(D).又由引理2 知

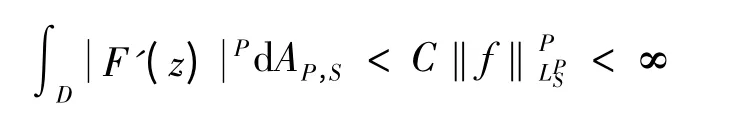
再由引理1 得知F(z)的正边值F+(t)∈LPS(D).

最后，由Plemelj 公式［2］有

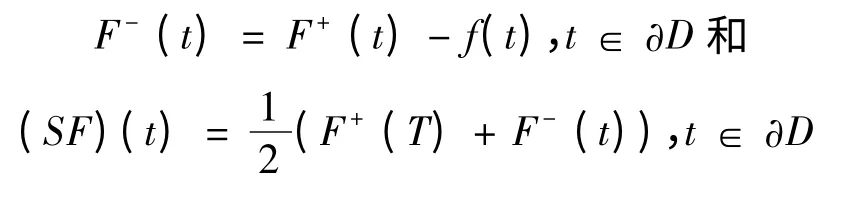
都在空间LPS(∂D)中.

3 结论

本文证明了在单位圆圈上作为Hölder 函数空间的某些推广空间LPS是奇异积分算子的不变子空间.这样的结论在常用的LP(R)空间以及Hilbert变换是不对的(那里只是两个非平凡的无穷维不变子空间).本文的工作是把经典的解析函数边值问题和奇异积分方程理论推广到现代函数空间的准备.

［1］ 路见可.解析函数边值问题教程［M］.武汉：武汉大学出版社，2009.

［2］ Mikhlin S G，Prossdorf S.Singular integral operators［M］.Berlin：Springer-verlag，1986.

［3］ Li X，Long Y Y，Shi P P.The thermal effect of antiplane crack in a functi-onally graded piezoelectric strip under electric shock［R］.The 13th International Conference on Fracture，June 16 -21，2013，Beijing.

［4］ Slobdrain R J，Rioux C，Piche M.A review of metallic fractal aggregates［J］.Open Journal of Metal，2011(1) ：17 -24.

［5］ Lin J，Du J Y.Stability of displacement to the second fundamental problem in plane elasticity［J］.Acta Math Sci，2014(34) ：125 -240.

［6］ EM.Singular integrals and differentiability properties of functions［M］.Princeton：Princeton University Press，1971.

［7］ Arcoggin N，Blasi D，Pau J.Interpolating sequences on analytic Basov type spaces［J］.Indiana Unvi Math J，2009，58(3) ：1281 -1317.