OFDM电力线通信系统抗噪性能分析

郑雪娇，焦 键

(重庆科创职业学院机电学院，重庆 永川 402160)

电力线通信是一种采用现有的电力分布式网络中的基础设施作为传输介质的通信技术［1］，它可以提供一个有限带宽信道.该系统不仅通过使用现有电力线路的基础设施网络达到节省布线的目的，而且传输数据时不易被其他任何子网络入侵，比无线和电话线路等常用信息传输线路更加安全.该项技术在智能楼宇通信自动化网络改造中尤为重要.然而，电力线不是专用通信信道，它所承受的既有外界干扰，又有内部噪声.因此，该通信信道更加复杂.噪声干扰会使接收端信号误码率增加，从而影响整个通信质量.因此，有必要对电力线中的噪声干扰进行有效分析，以提高电力线通信系统的抗干扰能力及数据传输速率.

近年来，数字通信系统的研究发展很迅速，它为有线和无线传输提供高质量的通信环境.多载波调制一直被认为是有限带宽信道的高效调制方案.正交频分复用(OFDM)是一个在有限带宽环境下的一个数字数据传输方法，是数字多载波通信中技术成熟且性能优良的技术［2］.因此，对于电力线通信，OFDM 被认为是其中一个最有效的调制方案.本文研究的目的是为电力线通信实现一个OFDM 通信链路，利用Matlab 和嵌入数字信号处理(DSP)系统进行虚拟发射机和接收机的模拟操作，并通过加入噪声来干扰信号以进行系统性能的分析.图1是电力线通信传输示意图.

图1 电力线通信系统框图

1 电力线噪声

众所周知，电力线传输数据是解决通信“最后1 公里”问题的有效手段.然而，电力线通信系统却存在着比普通通信系统更为复杂的噪声和干扰问题［3，4］.电力线噪声类别可以分为5 种:

①一个相对低的功率谱密度的有色背景噪声，大量低功率噪声来源的总和;

②窄带噪声，主要是由振幅无线电广播电台入口的振幅调制正弦信号引起;

③异步的电源频率的周期脉冲噪声，主要是供电电源的切换引起;

④同步的电源频率的周期脉冲噪声，主要是日用电器中整流二极管的作用引起;

⑤非周期脉冲噪声，电力网络瞬态状态变化引起.

除了加性高斯白噪声，以下是对电力线影响较大的两个噪音的分析.

1.1 有色背景噪音

有色背景噪声是由电力线上各种噪声源产生的组合干扰，是一种随时间缓慢变化的随机干扰，其功率谱密度(PSD)随频率增加而减小.

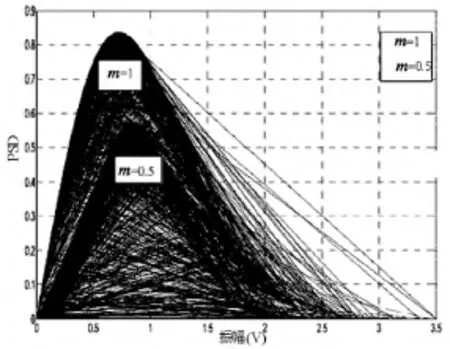
图2 m=1 和m=0.5 时的Nakagami 概率密度函数

文献［5］中，通过来自实验室和多弧离子镀真空的测量值，一个广泛研究的噪声振幅频谱显示了时域噪声频谱的概率分布类似于Nakagami－m 分布，它的概率密度函数可表示为:

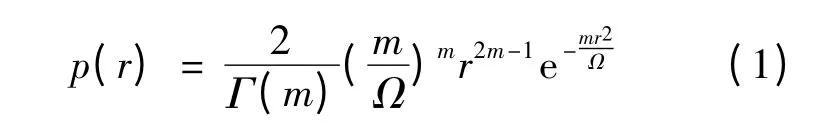
其中:r 是随机变量，p 是相应随机变量的概率.Γ(m)是伽马函数，m 是Nakagami 衰落和瑞利分布之间的相似度.此项研究的仿真表明，m=1 时，Nakagami 的概率密度函数与瑞利分布的概率密度函数一样;当m ＞1 时，Nakagami 比瑞利分布的概率密度函数拥有较小的方差和较大的平均值，当m ＜1 时，恰好相反.图2表示m 取值不同时，Nakagami 概率密度的分布.

1.2 脉冲噪声

通过统计分析方法，利用脉冲噪声干扰信道［6］分析了OFDM 系统的性能.通过假设大量统计独立的噪声干扰来创建脉冲噪声模型，根据每个干扰产生的噪声带宽，脉冲噪声通常分为3 类(上述的③④⑤).本文主要关注周期脉冲噪声模型.值得一提的是，噪声带宽认为是相当或低于干扰通信系统的带宽，因此在模拟接收机瞬态效应阶段可以忽略不计.加入脉冲噪声的信道模型可表示为:

其中:s 表示传播的符号，n 表示A 类分布的随机变量，r 表示接收到的值.

此外，为了模拟一直存在的热接收机噪声，添加了高斯噪声部分.A 类噪声的概率密度函数可表示为:

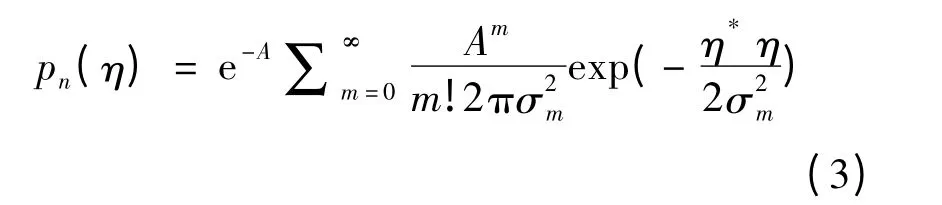
其中:η*表示η 的共轭，

参数A 表示脉冲指标，它是由单位时间脉冲的平均数和发送脉冲进入接收机的平均持续时间提供.当A →∞时，噪音呈现高斯分布且产生更多的结构化噪声.T 是高斯平均功率和脉冲噪声分量平均功率的比值.

2 噪声模型及仿真分析

在仿真前，这里首先分析实测噪声信号的特点.

1)周期性:电力线谐波噪声以交流电频率(FAC)的整数倍出现，存在周期性的倾向.产生这种周期性噪声的原因是由于许多用电设备会在工频交流电基波的某个固定相位上释放出噪声.因此，噪声在时域中呈现一定的周期性.

2)连续性:在实际情况中，由于有大量的用电设备同时释放出噪声，而这些噪声的瞬时功率、周期、相位等又变化很大，各不相同，因此最终会在电力线上产生时不变的连续噪声.幅值较低的干扰就属于这种噪声，表现为平均功率较小，但频谱很宽且持续存在.

3)随机性:电力线上存在许多随机发生的噪声，这种随机噪声通常是由于高压开关的操作、雷电、较大的负荷变化、电力线路上的短路故障等引起的，往往是能量很大的脉冲噪声或脉冲噪声群，持续时间较短，但能量很集中，频谱也很宽.

4)多变性:测量表明，低压电力线上的噪声存在多变性.这种多变性表现在两个方面.首先是因时而变，即在不同时刻，噪声的频率、强度都各不相同.其次是因地而变，即在不同的低压电网之间，噪声情况各不相同;而在同一个低压电网之内，不同地点的噪声情况也不相同.

在此分析基础上，通过Matlab 软件仿真出随机噪声与有色背景噪声模型，如图3所示.然后将该噪声信号模型分别混入到OFDM 系统中.

图3 (a)随机噪声模型

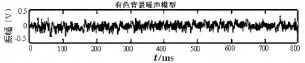
图3 (b)有色背景噪声模型

图4显示了在AWGN 信道中，不同的调制对应的BER 曲线.图5表示有/无卷积编码的AWGN 信道BER 比较.

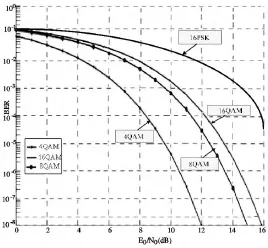
图4 不同调制条件下BER 的比较

从图4中可看出，不同阶的QAM 调制性能差异比较明显.16QAM 调制可有效地利用带宽，并在带宽利用率上比16PSK 更有效，它在抗误码性能方面优于16PSK 调制.同时，低阶的4QAM 调制性能优于8QAM 与16QAM.这是由于在AWGN信道噪声环境下，调制的阶数越高，抗干扰性能越差，因此低阶QAM 调制可使性能得到改善.

为了分析前向纠错(FEC)对系统性能的影响，在仿真系统中采用卷积码.卷积码为(7，2，1)码，其译码采用维特比译码，各子信道上的调制方式为分别采用不同阶的QAM 调制.图5显示了有/无卷积编码的AWGN 信道误码率.

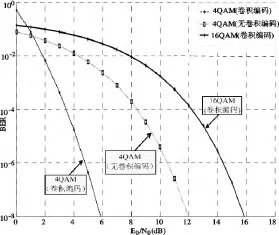
图5 有/无卷积编码的AWGN 信道BER 比较

从图5可看出，高斯白噪声信道中使用卷积码的情况下，前向纠错可大大提高系统的性能.当误码率为10－4时(4QAM 调制)，卷积码的编码增益为大约4.5 dB，对于更低的误码率(10－8)，编码增益可以达到6 dB 左右.16QAM 调制虽然采用了卷积码，但是由于该高阶调制提供的数据率较低，所以未能达到理想性能.

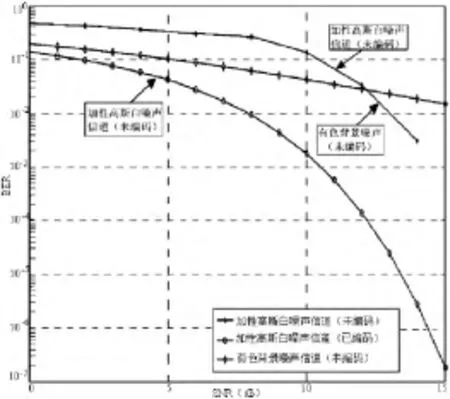
图6 信道混入不同噪声的BER 比较

图6表示未编码高斯白噪声、卷积编码高斯白噪声和有色背景噪声对信道误码率的影响.显然，在未采用前向纠错的情况下，有色背景噪声对信道的影响比较平缓.噪声幅度较小时，随机噪声(加性高斯白噪声)对信道影响较大，但是当噪声幅度提高时(SNR ≈12 dB)，随机噪声对信道的影响明显下降，此时，对信道影响较大的则为有色背景噪声.当采用前向纠错技术时，AWGN 信道传输的BER 很小，此时的传输比较理想.

3 结论

本文首先分析OFDM 电力线通信系统中的主要噪声干扰，并根据实测模型分别建立噪声信号的仿真模型.在仿真阶段，针对建立的噪声模型，分别混入到通信信道中，并采用不同阶的调制方式.结果表明，低阶QAM 调制可使性能得到改善.最后，对于OFDM 系统，采用前向纠错技术对信道误码率进行分析.结果表明，采用卷积编码前向纠错可有效降低加性高斯白噪声信道接收端信号的误码率，大大提高系统的性能.

［1］ 张林山，杨晴，崔玉峰，等.面向三网融合的低压配网通信技术综述［J］.云南电力技术，2011(1) ：28 －30.

［2］ 胡心怡，方睿，李日欣，等.OFDM 技术发展综述［J］.通信技术，2010(8) ：132 －134.

［3］ 陈风，郑文刚，申长军，等.低压电力线载波通信技术及应用［J］.电力系统保护与控制，2009，37(22) ：188－195.

［4］ 郭昊坤，吴军基，衡思坤，等.低压电力线通信信道噪声建模及仿真［J］.电力系统保护与控制，2012(13) ：61 －66.

［5］ Meng H，Guan Y L，Chen S.Modeling and analysis of noise effects on broad－band power－line communications［J］.IEEE Transactions On Power Delivery，2005，20(2) ：630 －637.

［6］ 应展烽，吴军基，郭昊坤，等.含周期性脉冲噪声的低压电力线噪声建模研究［J］.电力自动化设备，2013(9) ：58 －63.