考虑固结的透水管桩沉桩全过程有限元模拟

周小鹏，梅国雄

（1.南京工业大学 交通学院，南京 210009；2.华润置地（宁波）有限公司，浙江 宁波 315000）

1 引言

沉桩施工中超静孔压的产生和消散将对土体强度以及地基承载力产生很大的影响。过高的超静孔隙水压力妨碍施工进度，甚至威胁邻近建筑物和构筑物的安全[1]；沉桩结束后，超静孔隙水压力消散会影响土体的强度，进而影响土体承载力时效性[2]。

工程实践中，常采用预钻孔取土打桩、合理安排打桩顺序、控制打桩速率、设置排水砂井或塑料排水板等方法减小挤土效应影响[3]。但其过程皆通过添加额外施工条件实现其控制效果，所添加额外施工条件并没有耦合至现有施工措施或技术产品中，因此，不免带来了工程效率上的问题，这与现代土木工程建设节奏相悖。结合当前地基处理技术呈现出由“单一”向“多元”转化的趋势，本文提出透水管桩[4-5]技术（如图1 所示），能较好的解决以上问题：①排水通道位置（孔）根据桩周土体的位置和性质，在预制桩生产过程中按需设置于桩身；②在沉桩过程中，排水通道位置是堵上的；沉桩结束，可方便打开或者融化，形成排水通道。

透水管桩属于新型静压桩，其沉桩贯入过程与普通静压桩相同，主要区别在于沉桩贯入完成后桩周土体的固结过程。对于岩土贯入问题的研究常基于圆柱孔扩张理论（cavity expansion method，简称CEM）展开，通过CEM 解释沉桩挤土机制，以及沉桩挤土过程中超静孔压的变化规律已相当成熟。

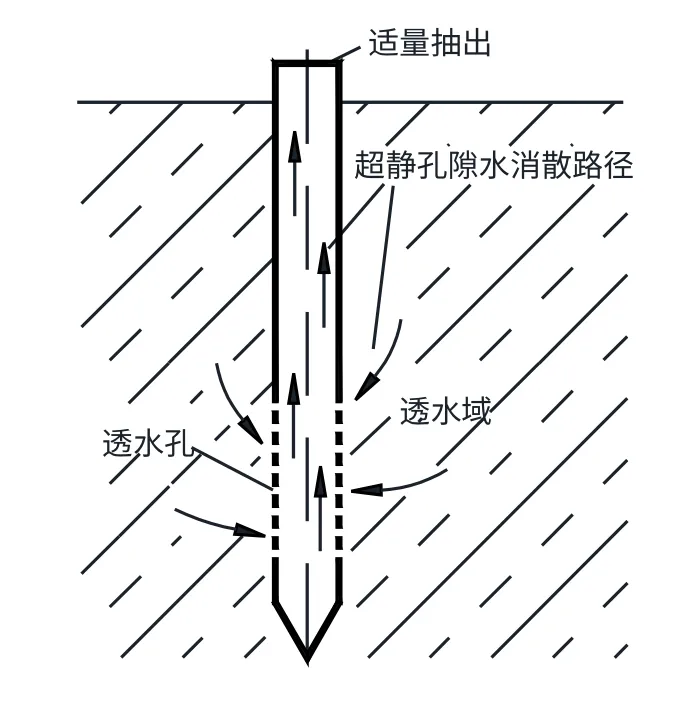
图1 透水管桩Fig.1 Permeable pile

CEM 提出之后，经过Vesic[6]，Randolph 等[7]的发展，已经成为解决沉桩对周围土体影响应用最为广泛的一种方法，这与CEM 形式简单、易于求解密不可分[8]。本文基于有限元法对透水管桩贯入挤土过程以及桩周土体固结过程进行模拟，并且对比CEM 验证模拟过程,阐述沉桩过程位移场、超静孔压场变化规律等。

2 有限元模型

沉桩挤土过程属于复杂的岩土贯入问题，本文基于ABAQUS 数值软件，采用有限元数值法[9]模拟透水管桩贯入挤土过程以及沉桩后桩周土体固结过程。

2.1 基本假定

（1）简化实际三维沉桩问题，以轴对称方式模拟计算；

（2）桩体采用离散刚体单元，计算过程中不考虑桩身强度影响；

（3）土体为均质连续的弹塑性体，计算模型本构采用修正剑桥模型本构；

（4）桩土表面法向接触采用硬接触，允许接触后分离，切向可以滑动；

（5）计入土体自重影响，计算中采用添加体力的方式替代；

（6）通过添加位移边界[10]实现贯入过程，贯入过程中桩周土体处于不排水状态。

2.2 模型尺寸及参数

以轴对称简化计算单桩挤土贯入三维问题，计算模型及其尺寸如图2 所示。

桩体直径Φ=0.5 m，桩体单元采用离散刚体计算，不考虑桩身强度影响，沉桩贯入深度为10 m，采用添加位移边界方式[10]实现。

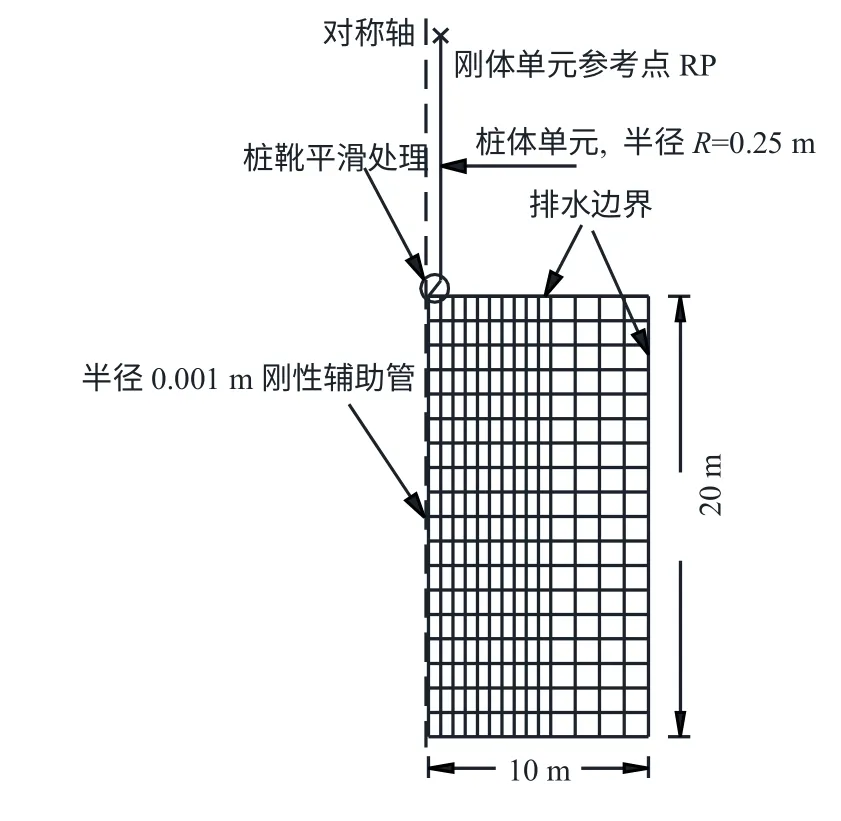
图2 计算模型Fig.2 Calculation model

考虑到挤土贯入过程超静孔压分布范围一般达到10～20 倍桩径[3]，土体径向尺寸取R=10 m，结合桩体贯入深度，土体竖向高度为20 m。

土体计算采用修正剑桥（modified cam-clay，简称MCC）本构，ABAQUS 有限元计算中剑桥模型的建立需要配合多孔弹性模型，土体参数来自扬州大学校园内三轴试验土体[11]。土体相关性质参数如表1、2 所示。

表1 多孔介质弹性模型参数Table 1 Parameters of porous elastic

表2 黏土塑性模型参数Table 2 Parameters of clay plasticity

3 有限元退化处理及对比验证

3.1 模型退化

透水管桩主要区别于普通静压桩在于其桩身表面一定区域内透水，即透水管桩桩身存在透水域。本文通过透水域区分透水管桩和普通静压桩，为研究方便，定义透水域大小（permeable area 简称PA）如下式（1）：

式中：L1表示桩身透水域竖向长度；L0表示透水管桩长度。

结合上式，PA=0 表示普通静压桩；PA≠0 表示透水管桩。因此，PA 从0 到非零过程即是普通静压桩到透水管桩过渡过程，如图3 所示。

对于沉桩贯入过程，由于时间较短，可假设桩周土体处于不排水状态，因此PA 大小对计算结果没有影响，即普通静压桩和透水管桩于贯入阶段模拟计算均一致。

为计算方便简洁，采用PA=0 状态即退化为普通静压桩模型下有限元计算结果进行对比验证。

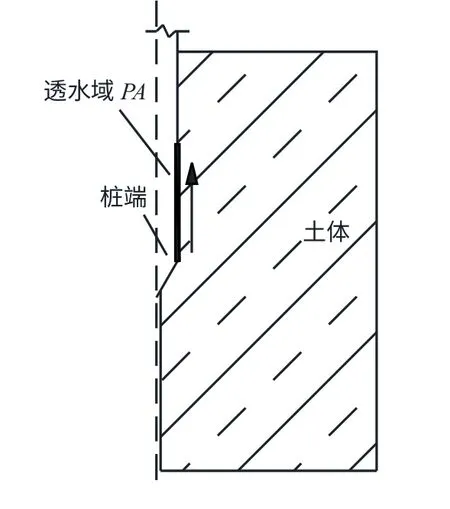
图3 退化模型Fig.3 Degradation model

3.2 对比验证

对于沉桩贯入机制，圆柱孔扩张理论（CEM）解释较为成熟合理，可作为验证标准[8]。沉桩贯入过程结束后，桩周土体径向位移场、超静孔压场有限元计算结果与CEM 解析计算结果对比如下。

（1）径向位移场对比

CEM 中泊松比υ=0.5时，和修正剑桥理论下按不排水假设的情况得到的径向挤土位移是一样的，即桩贯入饱和土的过程视为不排水过程，土体中的圆柱孔扩张视为等体积变化过程，根据等体积公式得到桩周土体径向表达式为

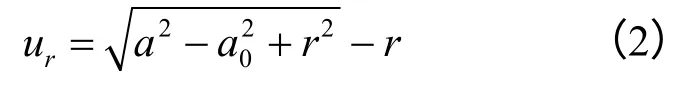
式中：a、a0分别表示小孔扩张后半径和扩张之前初始半径。

取贯入过程结束后不同深度下土体径向位移有限元计算结果与CEM 径向位移结果对比，其结果如图4 所示。图中可知：

①径向挤土位移量随径向距离呈非线性衰减，最大衰减幅度集中在一倍桩径范围内，参照CEM机制，即一倍桩径范围内土体处于塑性变形阶段，甚至贴近桩身部分土体结构完全破坏；

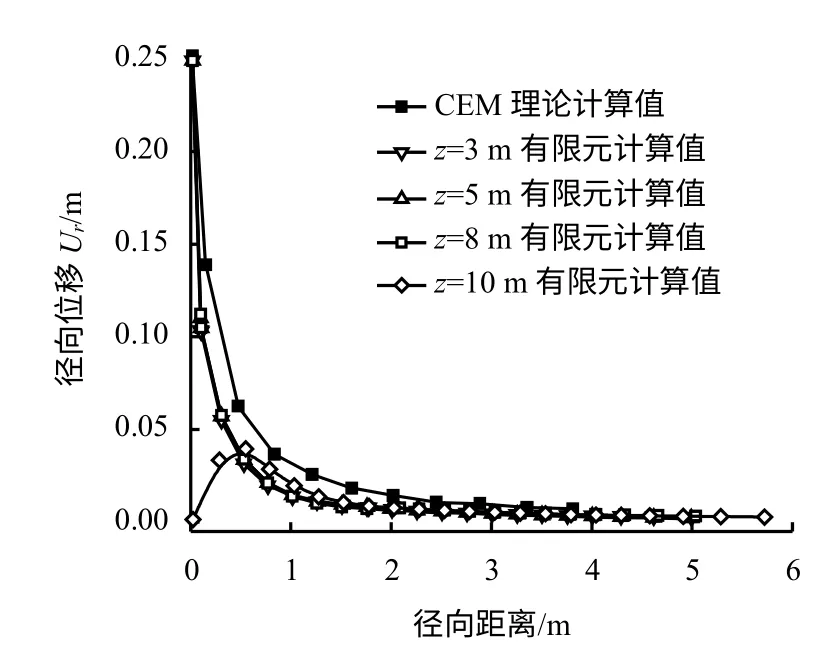
图4 沉桩结束后不同深度下土体径向位移对比Fig.4 Radial displacement comparison of soil under different depths

②径向3 m 范围外土体的位移量变化趋于平缓，参考CEM 机制，即3 m 范围外土体处于弹性变形阶段；

③除桩端位置，不同深度下（z=3、5、8 m）土体径向位移与CEM 理论计算值基本重合，即桩身段土体变形机制较为符合CEM，且计算准确；

④桩端位置土体径向位移随径向距离呈现出先增后减的趋势，此段土体变形较为符合球孔扩张假定，CEM 中未考虑竖向变化因素，存在局限性，于桩端位置不适用；

⑤整体而言，沉桩贯入结束后有限元位移计算结果合理，与CEM 计算结果相吻合。

（2）土体内超静孔压场对比

取贯入过程结束后z=9 m、z=10 m 深度处超静孔压有限元计算值与CEM 超静孔压计算值对比，其最终结果如图5 所示。

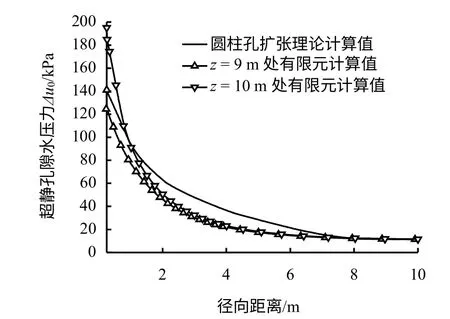
图5 沉桩结束后超静孔压对比Fig.5 Initial excess pore pressure contrast at the end of pile penetration process

图中可知：z=9 m、z=10 m 深度处有限元计算曲线和理论计算曲线变化规律一致，大小相近，初始超静孔压沿径向均呈非线性衰减，与理论解析计算值较为吻合。

整体而言，沉桩贯入结束后有限元计算结果合理，与CEM 计算结果相吻合，可用于进一步分析研究。

4 透水管桩沉桩及桩周土体固结分析

透水管桩属于新型静压桩，其贯入过程与普通静压桩（PA=0）相同，区别在于沉桩贯入完成后桩周土体的固结过程。

因此，透水管桩沉桩过程通过PA=0 的静压桩模型实现，桩周土体固结过程以PA=1 的理想透水状态分析。

4.1 透水管桩贯入过程分析

（1）径向挤土位移分析

图6 所示为土体表面径向位移随贯入过程分布变化。贯入过程中，靠近桩身处位移较大，贴近桩身处土体位移量达到0.25 m，即一个桩体半径，并且沿径向呈现指数型衰减；随着贯入深度的增加，不同时刻土体表面径向位移变化不大，趋于恒定。

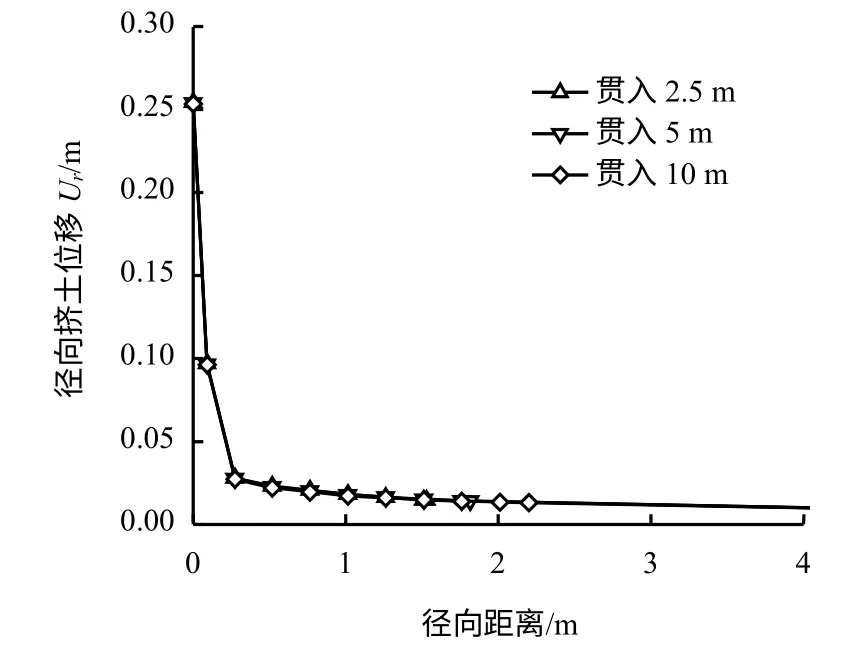
图6 贯入过程土体表面径向位移径向分布Fig.6 Radial displacement distribution of pile penetration

图7 所示为贯入结束后不同径向范围内土体径向位移规律。图中可知，沿深度方向土体径向位移于土体表面附近0～1 m 左右出现突增后又迅速减小；4～6 m 段土体径向位移稳定；超过贯入深度10 m 后，即11～20 m 深度土体径向位移逐渐衰减至0；径向表现为越接近桩身挤土位移量越大。

图8 所示为贯入过程中3 倍桩身半径处土体径向位移随贯入过程变化情况。在贯入过程中，最大位移始终出现在桩端位置，图中所示，当贯入2.5 m时，最大位移出现在z=2.5 m 处，贯入5 m、10 m时，最大挤土位移分别出现在z=5 m、z=10 m 处，整体上，深度方向变化规律和图7 相似，在土体表面附近有波动即先减小后增加，桩身中部位置，挤土位移变化缓慢，呈现出平衡趋势，超过桩端位置深度土体，其挤土位移快速衰减至0。

图7 沉桩贯入结束后不同径向距离下径向位移深度分布Fig.7 The depth distributions of the radial displacement at the end of pile penetration

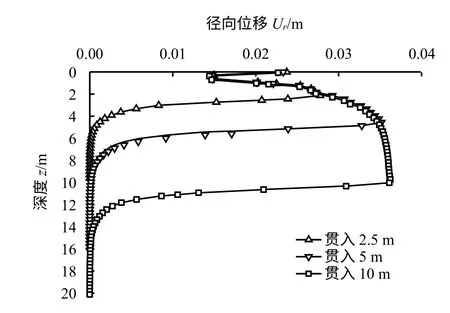
图8 贯入过程中径向3r0处径向位移深度分布Fig.8 The depth distributions of the radial displacement in the 3r0range in pile penetration

（2）竖向挤土位移分析

贯入过程中及结束后竖向挤土位移如图9、10所示。图中位移正负大小代表挤土方向，即负值表示向下挤土压缩，正值表示土体向上隆起。

如图9 所示表示贯入过程中径向3r0处不同时刻的竖向位移情况。以贯入5 m为例，沿桩身方向，竖向位移表现为：土体表面附近有明显的隆起变形，随着深度增加而减小，深度到达2 m 时隆起变形消减至0，之后都是向下压缩变形，5 m 位置即此时的桩端位置处，位移值最大，而后竖向位移随深度逐渐减小到0；图中竖向位移有累加的现象，随着贯入深度增加，出现在桩端附近的最大竖向位移值也逐渐增大，最终在贯入过程结束后，在桩端附近出现最大竖向位移。

图10 中，①不同径向距离下，土体表面都出现了隆起变形，而且越靠近桩身，其变形越大，图中径向3r0处的隆起变形量是6r0处的两倍左右，达到0.04 m；随着深度增加，隆起变形都逐渐减小，不同范围内土体隆起变形影响深度不同，6r0处隆起变形在z=4 m 处消散至0；②竖向挤土位移，越靠近桩身越大，最大值都出现在10 m 位置处，即桩端位置，随着深度最终减小到0；

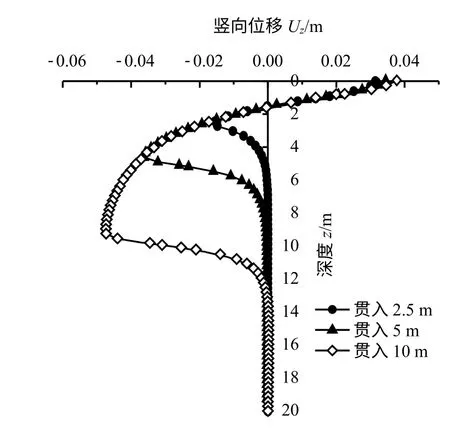
图9 沉桩过程中径向3r0处竖向位移深度分布Fig.9 The depth distributions of the vertical displacement in the 3r0range in pile penetration

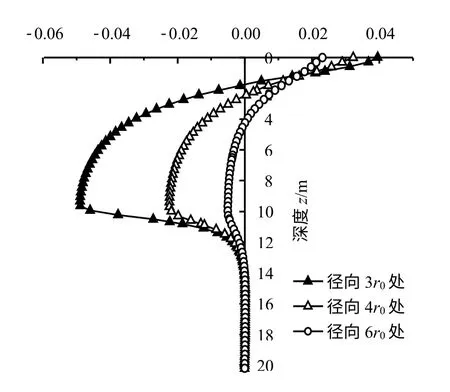
图10 沉桩结束后不同径向距离下竖向位移深度分布Fig.10 The depth distributions of the vertical displacement in different range at the end of pile penetration

（3）超静孔压场分布规律分析

贯入过程中超静孔压深度分布情况如图11 所示。图中贯入过程从0～10 m 结束，不同的贯入深度下孔压大小不一，但其基本规律相似：①超静孔压伴随着贯入过程逐渐增大，贯入到10 m 贯入过程结束，出现最大超静孔隙水压力；②贯入过程中，超静孔压深度方向分布不稳定，出现波动的情况，整体上，桩端位置处超静孔压处于峰值。沉桩贯入过程中由于土体处于不排水状态，地表位置超静孔压会出现负值情况，随着贯入过程进行，负孔压逐渐趋于0；③整体深度方向，超静孔压先从负值状态逐渐消散到0，而后增加到峰值状态，最后在2～4 m 后消散至0，即桩端下超静孔压影响范围是2～4 m。

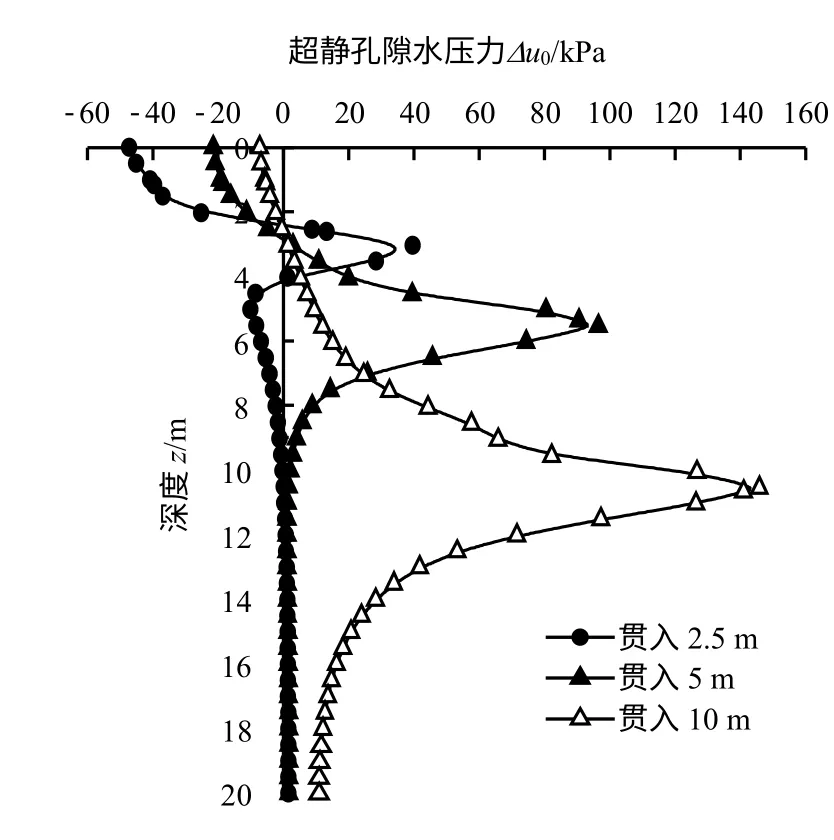
图11 沉桩过程中径向3r0处超静孔压深度分布Fig.11 The depth distributions of excess pore pressure in the 3r0range in pile penetration

沉桩结束后超静孔压径向不同位置处深度分布情况如图12 所示。①图中超静孔压大小沿径向衰减，越靠近桩身位置超静孔压越大，图中径向3r0位置处最大超静孔压达到150 kPa，远大于径向6r0位置处；②图中为贯入过程结束后超静孔压深度分布情况，贯入深度为10 m，图中可见10 m 处超静孔压位于峰值状态，整体而言，随深度增加超静孔隙水压力先增大后降低，最后区域稳定，但是不为0，因为模拟计算沉桩过程发生在不排水条件下，沉桩完成后，桩端以下土体中超静孔隙水压力无法消散，图中稳定在20 kPa 左右。

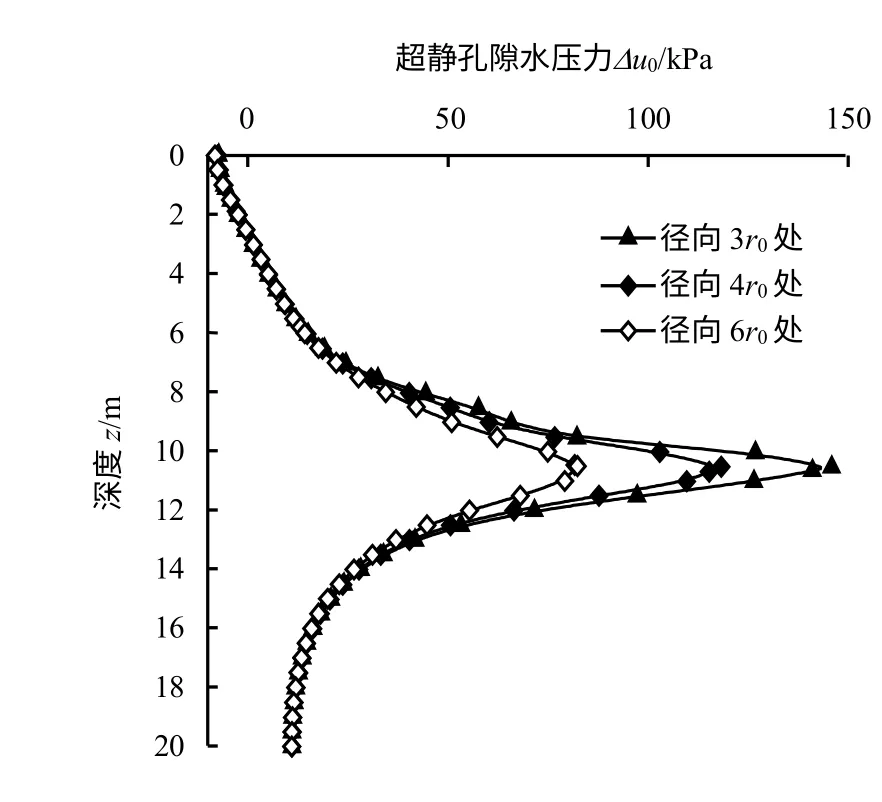
图12 沉桩结束后不同径向距离下超静孔压深度分布Fig.12 The depth distributions of excess pore pressure in different range at the end of pile penetration

4.2 透水管桩桩周土体固结分析

桩周土体固结性状很大程度上会影响桩基承载力时效性发挥。桩周土体固结过程即是桩周土体内超静孔压消散过程，本文以土体平均固结度[12]形式描述超静孔压消散变化规律，其表达式为

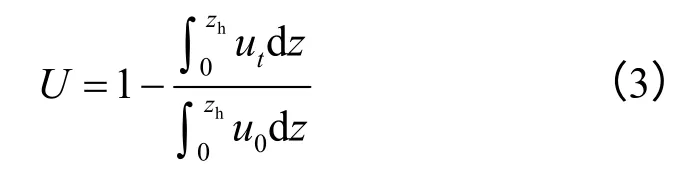
式中：u0、ut分别为初始时刻和t 时刻超静孔隙水压力；zh为计算土体厚度（土体厚度积分意义于本文有限元计算中为整个土体模型内所有节点处超静孔压之和）。

透水管桩以及普通静压桩桩周土体固结性状曲线如图13 所示，图中横坐标为时间坐标，采用对数形式，纵坐标表示桩周一定范围内土体平均固结度。

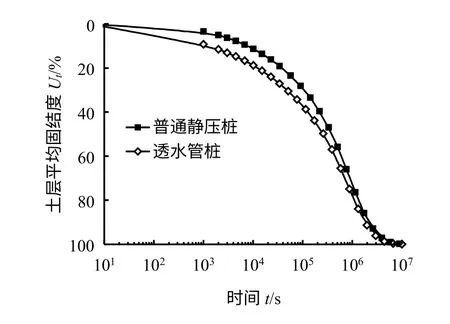
图13 静压桩和透水管桩桩周土体固结对比Fig.13 Consolidation contrast of soil around static pressure pile and permeable pile

整个贯入过程以及固结过程中，桩基承载力将会受到挤土、固结排水的影响。①贯入挤土过程桩周土体被压实，土体孔隙比等参数均会增大，进而对桩基承载力有一定的提升；②根据有效应力原理[12]，贯入结束后土体固结过程中，随超静孔压的消散，桩基承载力又将提升，因此可以考虑通过加速超静孔压的消散促进桩基承载力的发挥。

对比图中透水管桩和静压桩桩周土体固结曲线可以看出：桩周土体达到相同固结度时透水管桩耗时均短于静压桩耗时，图中表现为透水管桩固结曲线均位于静压桩固结曲线内侧。

因此，相同固结时间下，透水管桩桩周土体所达到固结度高于静压桩，即透水管桩桩周土体内超静孔压消散更快，土体固结效率更高，这意味着采用透水管桩技术，桩基承载力发挥将更快。

为方便观察透水管桩与普通静压桩桩周土体固结对比情况，本文采用固结效率提升率Uprate描述，其定义式如下：

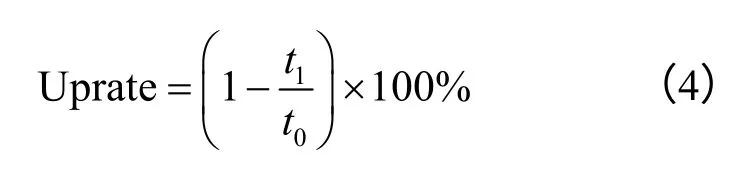
式中：t1表示透水管桩桩周土体固结耗时；t0表示普通静压桩桩周土体固结耗时。

结合式（4）桩周土体在不同固结度下，透水管桩耗时和静压桩耗时以及其固结效率提升数据整理如下表3 所示。

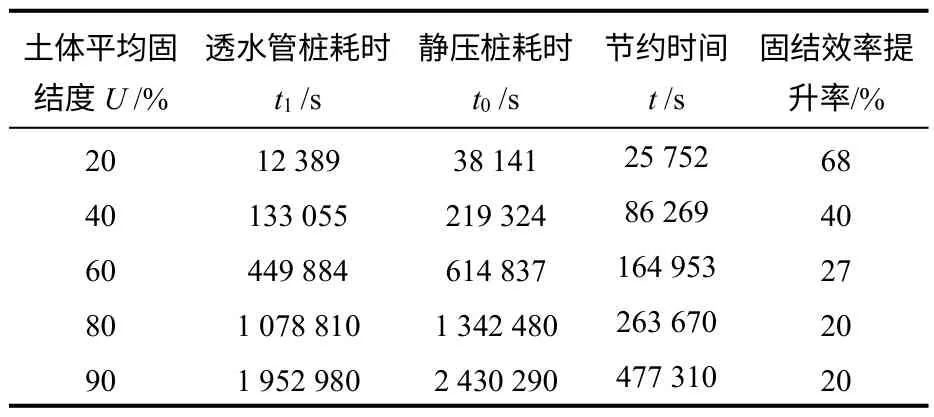
表3 相同土体固结度下固结效率提升率对比Table 3 Consolidation efficiency uprate contrast in the same consolidation degree of soil

由表3 可知：

（1）土体达到相同固结度时，透水管桩耗时均小于静压桩，在相同固结时间下，透水管桩模型中土体固结度均高于静压桩，因此，透水管桩对超静孔隙水压力释放方面有着明显的优势；

（2）土体固结度分别达到20%、40%、80%、90%时，对比静压桩，透水管桩下土体固结效率提升68%、40%、20%、20%，因此，特别是土体固结前期，透水管桩效果尤为明显，其固结效率直接提升68%，大大缩短了固结耗时。即透水管桩可在短期内实现桩基承载力快速提升，意义非凡。

之后随土体固结度增长，相比静压桩，透水管桩对桩周土体固结速率提升趋于平缓，具体趋势如图14 所示。

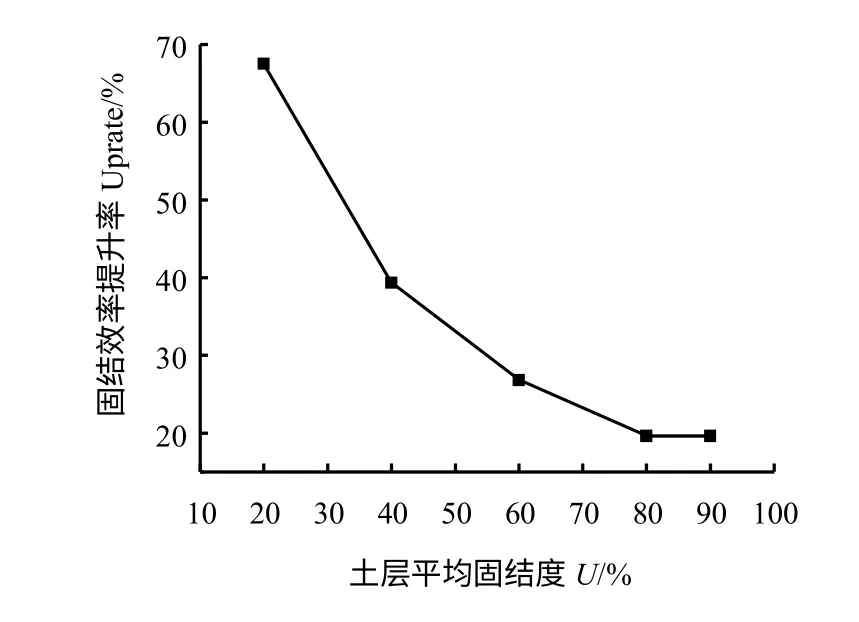
图14 透水管桩桩周土体固结效率提升率分布Fig.14 Consolidation efficiency uprate distribution of soil around permeable pile

另外，需特别说明：透水管桩对土体固结效率的提升并非保持恒定，其与土体自身渗透性质和固结过程中实时的超静孔隙水压力呈正相关，即土体渗透性越强，则透水管桩性能发挥越明显，土体中超静孔压越大，透水管桩对土体固结效率的提升越明显，其原因可参照半透水边界[13]释义，另作说明。

整体而言，对比静压桩，透水管桩对沉桩过程产生的超静孔隙水压力的释放有明显的优势，尤其在土体固结前期，其效果明显，能够快速的释放土体中超静孔隙水压力，可以短期内促进桩基承载力的提升，具有重要的研究价值。

5 结论

（1）控制透水域大小，实现透水管桩模型到静压桩模型的退化处理；

（2）于径向挤土位移场和桩周土体超静孔压场方面对比CEM 圆柱孔扩张理论，验证本文计算；

（3）阐述了桩体贯入过程中土体位移场、超静孔压场一般变化规律；

（4）对比静压桩和透水管桩桩周土体固结性状，发现透水管桩可以加速超静孔压消散，尤其是土体固结初期，效果极为明显，可以短期内促进桩基承载力的提升，具有重要的研究价值。

[1]张明义.静力压入桩的研究与应用[M].北京:中国建材工业出版社,2004.

[2]李向红,龚晓南.软粘土地基静力压桩的挤土效应及其防治措施[J].工业建筑,2000,30(7):11－14.LI Xiang-hong,GONG Xiao-nan.The compacting effect by static piling on soft clay foundation and the methods for prevention[J].Industrial Construction,2000,30(7):11－14.

[3]史佩栋.实用桩基工程手册[M].北京:中国建筑工业出版社,1999.

[4]梅国雄,梅岭,张乾,等.自适应减压排水管桩及其制备工艺:中国,ZL201110123235.6[P].2011-11-30.

[5]梅国雄,梅岭,张乾,等.塞孔式减压排水管桩及其制备工艺:中国,ZL201110123233.7[P].2011-12-14.

[6]VESIC A S.Expansion of cavities in infinite soil mass[J].Journal of Soil Mechanics &Foundations Div.,1972,98(3):265－290.

[7]RANDOLPH M F,WROTH C P.An analytical solution for the consolidation around a driven pile[J].International Journal for Numerical and Analytical Methods in Geomechanics,1979,3(3):217－229.

[8]陈文,施建勇,龚友平,等.饱和粘土中透水管桩沉桩机理及挤土效应研究综述[J].水利水电科技进展,1999,19(3):38－41.CHEN Wen,SHI Jian-yong,GONG You-ping,et al.Review of penetration and soil compaction effect of pile jacks in saturated clay[J].Advances in Science and Technology of Water Resources,1999,6(3):38－44.

[9]费康,张建伟.ABAQUS 在岩土工程中的应用[M].北京:中国水利水电出版社,2010.

[10]罗战友,龚晓南,王建良,等.透水管桩挤土效应数值模拟及影响因素分析[J].浙江大学学报:工学版,2005,39(7):992－996.LUO Zhan-you,GONG Xiao-nan,WANG Jian-liang,et al.Numerical simulation and factor analysis of compacting effects of jacked pile[J].Journal of Zhejiang University(Engineering Science),2005,39(7):992－996.

[11]李婷.考虑动态贯入过程沉桩挤土效应有限元分析[D].扬州:扬州大学,2012.

[12]钱家欢,殷宗泽.土工原理与计算[M].北京:中国水利水电出版社,1996.

[13]林政.软土的固结和渗透特性原位测试理论研究及应用[D].杭州:浙江大学,2005.