粉质砂土土钉墙水平位移与土钉轴力的FLAC3D 研究
2014-02-15单仁亮董洪国魏龙飞魏文康吕进阳
单仁亮,董洪国,,魏龙飞,魏文康,吕进阳
(1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.新兴保信建设公司,北京 100026)
1 引言
土钉墙作为一种可以边开挖边支护的的基坑支护方式[1],因其不单独占用工期、施工迅捷、工期短、造价低等一系列优点,自20 世纪80年代被引入我国以来,尤其是90年代以后,在我国的工程应用中取得了迅猛发展,已经广泛的应用诸如北京、上海、深圳等地的多种土质条件下的基坑工程中,甚至已成功应用于软土中的基坑工程中[2-4]。
土钉墙应用广泛,但实际工程中,由于现场人员水平参差不齐以及控制工程成本等原因,尤其是在二级或三级基坑工程中的土钉墙的监测工作难以得到重视,工程中通常只是通过对支护位移量测和地表开裂状态的观察等简单且易于操作的方法来对其进行监测。对于土钉墙墙体的位移监测,仅仅是在墙顶设置监测点,只有部分工程会在墙体深度方向上布置多个监测点[5],而对于土钉轴力的监测在建筑地基工程监测技术规范[6]中规定在二级和三级基坑工程中只是宜测和可测,具体工程中为控制费用一般不会对其进行监测。因此有必要对深度不是很大的土钉墙工程中的土钉轴力、墙体水平位移情况进行研究分析,以确定其变化规律和其间的关系,以便于更好地指导采用土钉墙作为支护方式的基坑工程的施工。
粉质砂土层为北京地区分布较为广泛的土层,在基坑工程中虽然没有粉质黏土和黏性土更为常见,但由于其自稳能力差,却是导致工程事故发生的主要土层之一。本文通过数值模拟方法对粉质砂土中土钉墙的工作特性进行了研究,分析了土钉轴力与墙体水平位移的变化规律和它们之间的关系。此外还进行了物理模型的土钉墙破坏性试验的研究,并与数值模拟情况加以对照,研究了土钉墙的破坏机制。
2 数值模拟试验
2.1 物理模型
如图1 所示,模型试坑尺寸(长×宽×深)为=3 500 mm×1 800 mm×1 800 mm,开挖部分的尺寸(长×宽×深)为=1 500 mm×1 800 mm×1 350 mm,土钉长1 200 mm,土钉按梅花形布置,具体布置尺寸见图1。
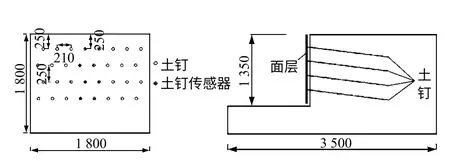
图1 物理模型布置图(单位:mm)Fig.1 Arrangement diagram of physical model(unit:mm)
如图2(a)所示,试坑的坑壁和坑底均做防水处理,并在两侧壁涂抹润滑的黄油后附一层摩擦系数极低的塑料薄膜来降低坑壁对土体的摩擦作用,试验中认为两侧壁与土体摩擦力为0。试验用的粉质砂土是从现场周边的正在施工的基坑中挖取的,且经过2 次筛分去除了粒径较大的颗粒的均质土体。在试坑土体填筑时先按每层20 cm 厚度虚铺,然后人工均匀夯实,以保证整个基坑中的土体为均质的。

图2 物理模型照片Fig.2 Pictures of physical model
模型具体支护参数见表1。基坑开挖分5 步进行,前4 步每步开挖深度为30 cm,第5 步为15 cm。开挖前,在墙顶预先施加10 kPa 的竖向均布荷载以模拟实际工程开挖中可能遇到的地表荷载。由于土钉采取预埋方式,具体程序为:开挖→面层施工→导线连接。面层施工时,先在开挖面上铺设一层φ 1 mm@40 mm 的铁丝网,然后通过土钉杆体端部预留的小孔,用铅丝将土钉与面层的纵横压筋进行绑扎,以使土钉与面层形成整体,并用水泥砂浆抹面以模拟喷射混凝土。图2(b)为第一个施工循环中的预埋土钉照片。在分步开挖时,前4 层每层开挖前即对土层进行取样,测量其物理力学参数,再进行开挖。土工试验测得土体的物理力学参数见表2。
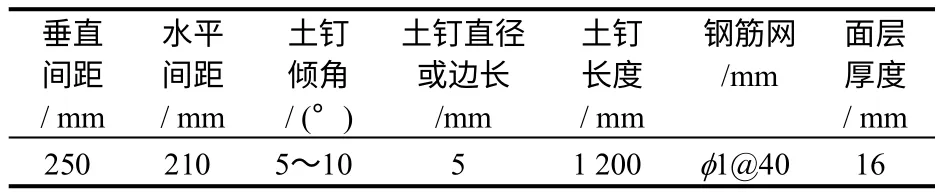
表1 模型支护参数Table 1 Timbering parameters of model

表2 模型土的参数(粉质砂土)Table 2 Parameters of model soil(silty sand)
开挖前先在墙顶施加10 kPa 的荷载,使土体固结。加载试验是在第5 次开挖及面层施工结束约48 h 后开始,卸掉预加的10 kPa 荷载,在墙顶土层上放置一块钢板,钢板距墙顶边缘10 cm,距两侧坑壁40 cm,可以保证对土体施加的荷载为均布荷载,然后,通过如图3 所示的加载系统实现加载,采用36 t 挖掘机提供反力。试验期间挖掘机保持不动,荷载通过千斤顶控制,并通过压力传感器监测施加荷载的大小,先施加9 kPa 荷载,恢复预加荷载,再按每级10 kPa 分级加载,各级加载时间间隔为30 min,本次试验共施加4 级荷载,墙体即发生破坏。
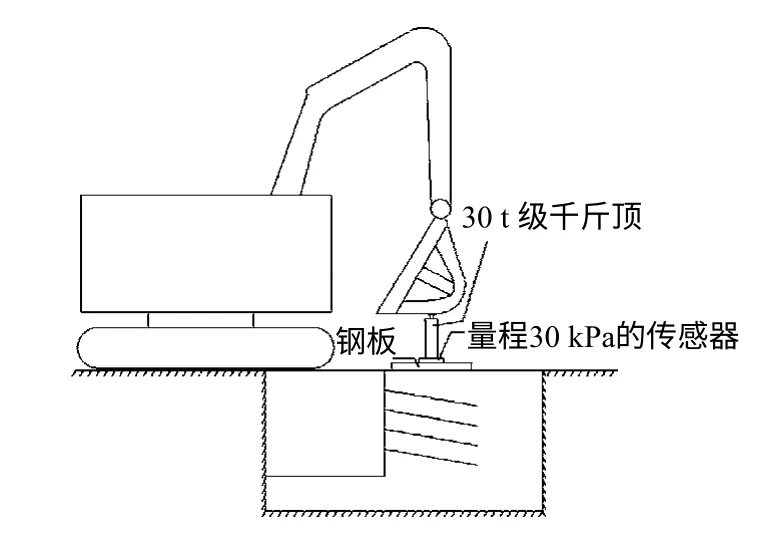
图3 加载系统Fig.3 Loading system
2.2 数值模拟模型
以表2 中的土的力学参数以及物理模型试验的尺寸和支护参数为基础建立数值模拟模型。土体的体积模量和剪切模量可以通过其与杨氏模量和泊松比之间的转化关系求得
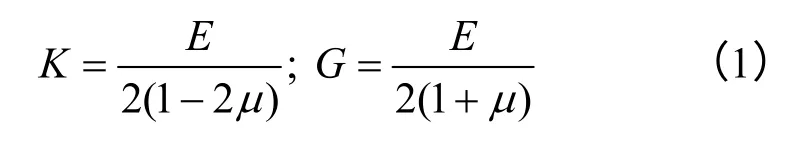
取土体的泊松比为0.3,则根据式(1)计算得到土体的体积模量K=5.6 MPa,剪切模量G=3.5 MPa,另设土的抗拉强度为0。采用FLAC3D中的Mohr-Coulomb 模型建立土体模型,见图4。数值模拟模型尺寸、墙顶荷载情况以及开挖支护步序均与物理模型试验的相同,左侧1.5 m 内的由上到下的5 层为开挖部分,前4 层厚度为0.3 m,第5层为0.15 m。基坑开挖结束后的支护体系见图5。
在边界条件方面,物理模型试验中对试坑两侧边界进行了刷油并贴塑料薄膜处理,可认为两侧边界与土体之间的摩擦忽略不计,即两侧墙体对试验土体只有垂直于墙面的约束,而没有摩擦约束。在FLAC 中,也将模型边界条件设为x 方向不可发生位移,而z和y 方向不做约束(即无摩擦力),保持和物理模型的一致。
图4 土体模型Fig.4 Model of soil
图5 支护体系图Fig.5 Sketch of supporting system
3 模拟结果分析
3.1 墙体水平位移分析
图6为开挖阶段水平曲线。由图可以看出,整个开挖阶段土钉墙墙体的位移都较小,直到开挖结束在墙顶分级施加竖向荷载之前,墙体最大水平位移仅有1.6 mm,约为基坑开挖深度的1.2‰,小于《基坑土钉支护技术规程》[5]规定的3‰到5‰的最大水平位移限制。从图6(b)为墙顶位移的实测结果和数值模拟结果的对比可见,墙顶位移在开挖阶段不断增大,且增速也在不断增加,实测结果大于模拟结果,主要是由于在物理模拟试验中土体开挖不可避免的对土体有扰动,使得墙顶位移量要大于模拟结果。
由朗肯土压力理论有土体的主动土压力系数Ka=0.57,临界高度 Z0=1.24 m。前3 次开挖中,由于总开挖深度不大,且基本小于土体的临界深度,墙体的水平位移很小,最大处也仅有第3 步开挖深度的0.67‰以及最终开挖深度的0.44‰。开挖第4层土后,基坑深度为h4=1.2 m,墙顶的均布荷载为10 kPa,折合为土体高度h=0.54 m,总高度为H4=h4+h=1.74 m,大于土体的临界深度。所以,从第4 层土体开挖后,土体变形量明显变大,尤其是第5 次开挖后,墙体最大水平位移达到了基坑开挖深度的1.2‰。
开挖阶段,土钉墙的最大水平位移位置并不是在墙顶,而是在基坑底部附近,这是由于上层土体中的土钉以及面层在开挖下层土体时已经发挥出了支护作用,可以很好地限制土体的变形,而下层土体开挖后土钉、面层的施工需要一定的时间,在支护发挥作用前,下层墙内土体作为主动区,失去了被开挖掉的基坑内被动区土体的支撑,会产生较大变形,同时上层土体由于土钉和面层的限制积聚了一定的应变能也要通过从下部无支护区域土体的变形来释放,引起下层土体进一步迅速变形。每次开挖后,上层土体只是产生一定的变形,而新开挖土层却产生较大变形量。因此,施工时墙体水平位移的监测点不能只布置在墙顶附近,也应该在坑底附近布置测点,尤其是在基坑开挖深度逐渐增大的情况下需要加强对墙体水平位移的监测,对土钉墙底部的监测。
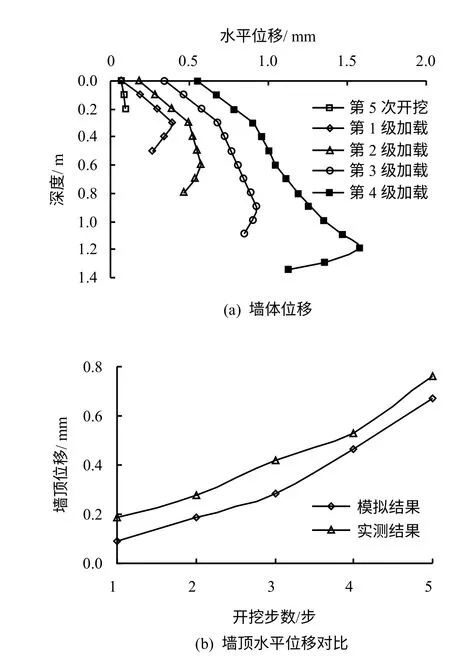
图6 开挖阶段墙体水平位移曲线Fig.6 Horizontal displacement curves of wall in excavation phase
实际工程中,某些土钉墙在施工结束前安全方面往往不存在问题,但在基坑开挖结束到肥槽回填之前的这段土钉墙的使用时间,由于工程上部结构的施工等,使墙顶出现了超载,如车辆在墙顶附近停放,钢筋、模板等建材在墙顶堆积等,导致墙体出现超出设计限制的位移而破坏。为了进一步模拟研究墙顶超载状况下的土钉的工作特性,在墙顶施加竖向的均布荷载,共加4 级,每级10 kPa。图7为加载状况下墙体水平位移。由图可以看出,加载状况下墙体水平位移发生了较大变化。
随着荷载的施加,墙体水平位移整体增大,但墙底位移增大并不明显,相反墙顶水平位移增大较剧烈,最终发展为顶部附近位移大于底部位移,该位移分布形态与珠江新城E2 区商住楼基坑工程[7]和南京市某明挖隧道支护工程[8]中对土钉墙墙体位移监测的结果相近;水平位移最大处由靠近墙底的深度为1.2 m 处逐渐发展为离墙顶较近的深度为0.3 m 处附近;第三级荷载施加且运算稳定后,墙体的最大水平位移为6 mm,约为基坑开挖深度的4.4‰,已接近于《基坑土钉支护技术规程》中规定的5‰的最大值;第四级荷载的施加,使墙体的水平位移急剧增大,位移最大处仍在墙顶下0.3 m 处,该处的位移达到了16 mm,已接近于第三级荷载下的3 倍,并且仍在继续增大,此时单纯的土钉支护已基本不能有效限制墙体位移的发展。
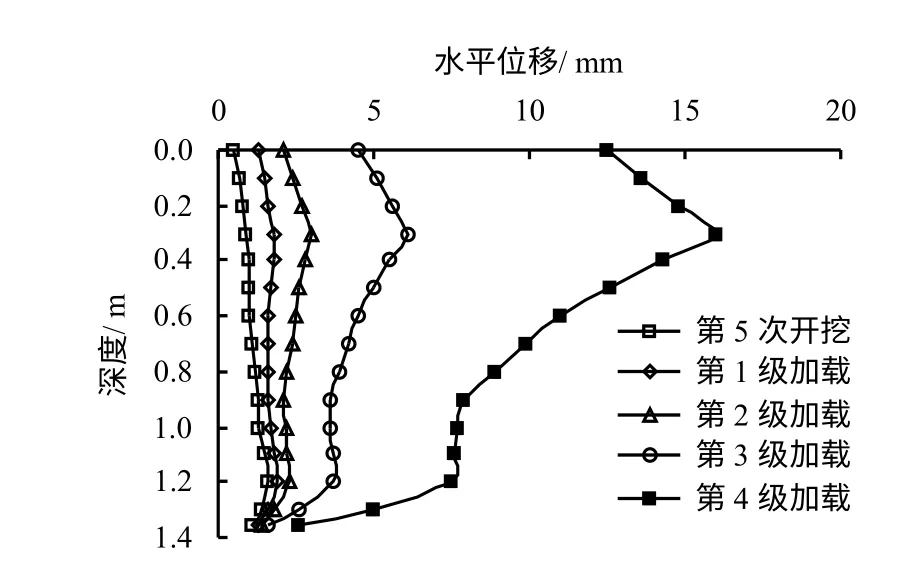
图7 加载状况下墙体水平位移Fig.7 Horizontal displacements of wall under loading circumstances
3.2 土钉轴力分析
模型中将每根土钉分为8 部分进行计算,通过FLAC3D中的History 命令来记录每根土钉的8 部分的轴力大小(见图8),并绘制成土钉轴力曲线显示了4 层土钉在各步开挖状况下的土钉轴力值。
由图8 可以看出,各层土钉的轴力均呈中间大,两端小的分布形态。土钉刚开始发挥支护作用时,轴力值最大处都靠近面层一侧,之后随着下部土体的每一步开挖,土钉轴力的最大处不断向远离面层方向移动。这是由于开挖后墙内及墙后土体失去了坑内土体对其的侧向支撑,而有向坑内移动的趋势,相应的由于土钉的存在,通过钉-土之间的摩擦作用阻止土体变形,墙内土体变形区域会随开挖深度的加深而逐步扩大,相应的土钉就要阻止更多土体的变形,其所承担的荷载就会增大并且向深部发展,从而在土钉轴力上的反映出土钉轴力不断增大,且最大处向远离面层方向移动。
由图8 还可以看出,第2、3 步开挖对第1 层土钉轴力增加最为明显,第3 步开挖对第2 层土钉轴力增量最大,第4 步开挖对第3 层土钉轴力值影响最大,之后开挖深度逐步增加而轴力增量却逐步减小。这一现象表明下层临近土体开挖对土钉影响最大,与开挖对墙体水平位移影响相契合。
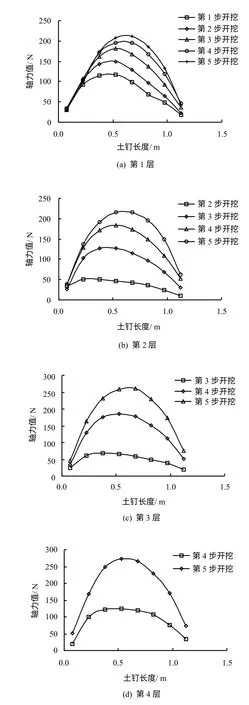
图8 开挖状况下各层土钉轴力值Fig.8 Axial forces of soil nailing in excavation phase
3.3 土钉轴力与墙体位移关系
由图9 可知,随着荷载的增加,各层土钉轴力值(轴力通过黑色区域的粗细进行比较,越粗轴力越大)均在增加,但分布上由开挖支护阶段的底部大,顶部小逐步发展为顶部大底部小,这主要是由于墙体的水平位移最大处从底部逐渐转移到顶部。(1)第5 步开挖后墙底向上0.3~0.4 m 处墙体水平位移最大,同样的距此最近的第4 层土钉轴力值也大于其他3 层;(2)第1 级加载状况下,距墙底0.3~0.4 m 处墙体水平位移仍然最大,但是墙顶向下0.3~0.4 m 附近的水平位移也在明显增大,同时该处土钉轴力亦在迅速增长;(3)到第2 级加载状况下,墙体沿深度方向水平位移基本一致,同样的,各层土钉轴力差距也很小,(4)第3 级加载后,墙顶向下0.3~0.4 m 处水平位移已为整个深度方向最大,距此较近的第1、2 层土钉轴力也均超过了第4层土钉。这充分说明了土体的变形和土钉轴力的发展过程是相协调的,土体的变形引起土钉轴力增加。由于水平位移与土钉轴力相一致,所以在二、三级基坑中,如无特殊要求,可以通过墙体位移的发展状况对土钉轴力分布情况进行初步判断。
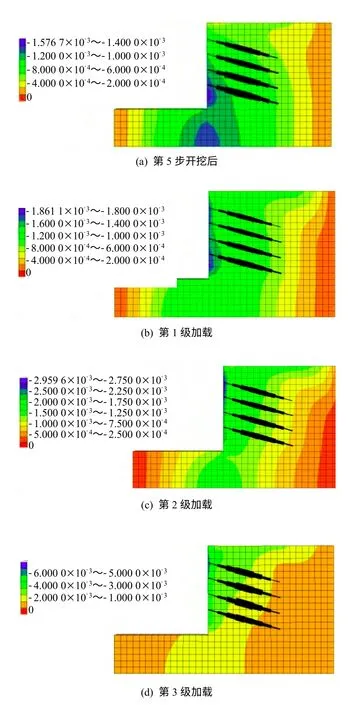
图9 各工况下水平位移云图及轴力图(单位:m)Fig.9 Diagram of horizontal displacements and axial forces in different phases(unit:m)
3.4 破坏过程分析
图10为第4级荷载施加后的不同时刻的土钉墙的水平位移和轴力变化图(图中轴力单位为N)。
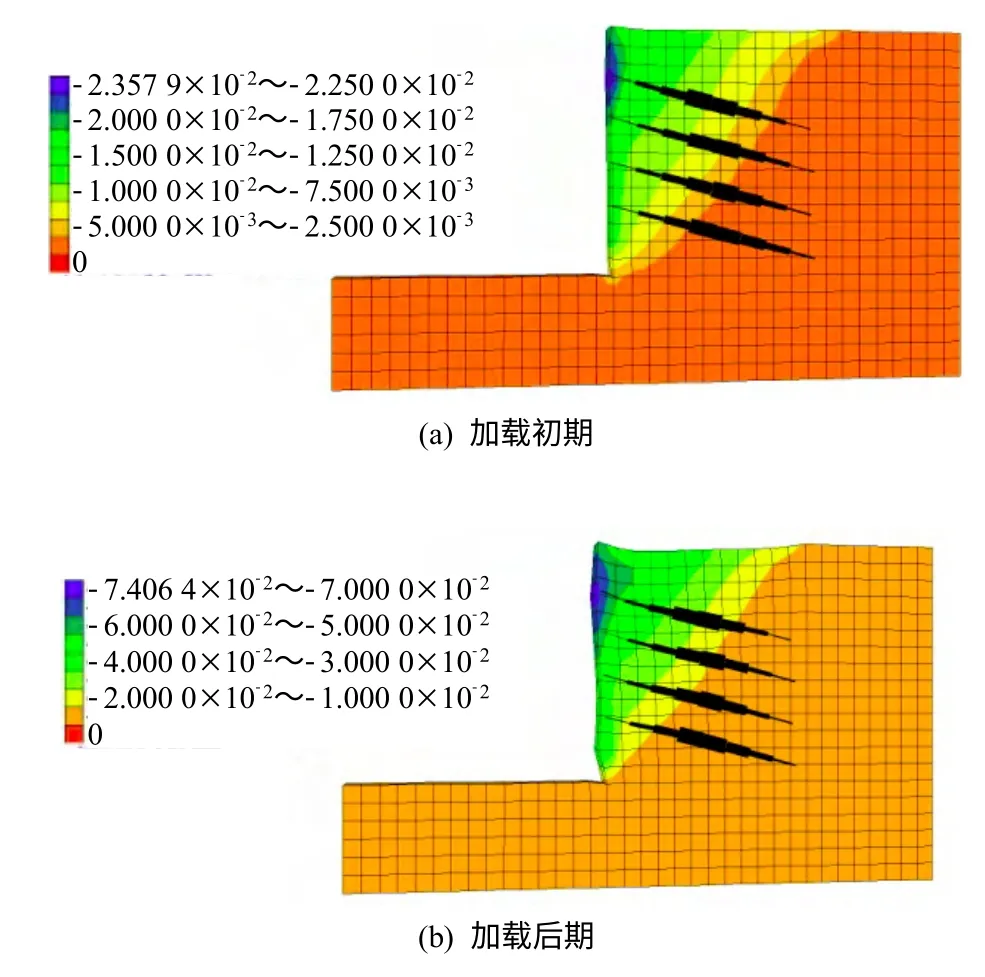
图10 第4 级加载下墙体破坏图(单位:m)Fig.10 Destruction diagram of wall under forth loading circumstance(unit:m)
由图10 可知,在墙顶继续施加第4 级荷载,加上开挖前在墙顶预加的10 kPa 竖向均布荷载,此时墙顶竖向荷载为50 kPa,在荷载作用下墙体进一步变形,并在水平位移图10(a)已可以判断滑动区的分布情况,此时墙体顶部已有较明显变形,最大变形量达到2.36 cm,随着时间推移,土体进一步变形,墙顶土体下陷,墙顶水平位移增大的同时,墙底水平位移也迅速增大,并在深度为1.2 m 处形成一个突起,模型中每一格表示0.1 m,可以判断滑动区宽约1.2 m,高约1.2 m,滑动面与水平面夹角约为45°。
图11为物理模型试验中土钉墙在第4 级加载作用下的破坏图。滑动区域高1.2 m 左右,宽1.3 m左右,出露部分破裂面角度为43°左右。数值模拟与物理模拟试验结果非常相近。此外,由图中还可以看出,墙体中下部位移较大,且明显大于墙顶位移,此现象也与数值模拟的结果相符。
在墙体破坏阶段,土钉轴力增加已不再明显,钉-土截面的摩擦阻力已达到最大值,面层部分也发生开裂,失去对墙体位移的限制作用,最后土钉墙失稳,逐步破坏。由于模型土体为均质土,且不存在软弱下卧层的问题,所以墙体的破坏形式为部分复合土体向下滑移的体内破坏,而不是整体失稳。

图11 物理模型破坏图Fig.11 Destruction diagram of physical model
4 结论
(1)开挖和加载过程中,土钉墙的水平位移是一个动态发展的过程,当土体与土钉组成的复合土体非常稳定时,整个深度方向,土钉墙的底部位移较大,随荷载施加顶部位移会迅速增大,当墙体要发生滑动破坏时,土钉墙的底部的滑裂面处的位移又会迅速增大并形成一个突起。
(2)土质为粉质砂土时,土钉墙的水平位移的最大值应控制在基坑开挖深度的4‰以下,大于4‰后应立刻采取其他辅助措施以保证墙体稳定,否则,墙体可能会迅速丧失稳定性。
(3)土钉轴力与墙体水平位移是协调发展的,水平位移较大处附近的土钉轴力也就大。在采用土钉墙支护的二、三级基坑工程中,如果没有条件监测土钉轴力时,可以依据对墙体位移的监测对其加以初步判断。
(4)土体为均质的粉质砂土时,土钉墙在破坏时的滑动区的高度和宽度基本一致,如果不存在软弱下卧层,则破坏形式为墙内部分土体向坑内滑动破坏。
[1]中国建筑科学研究院.JGJ120-99 建筑基坑支护技术规程[S].北京:中国建筑工业出版社,1999.
[2]应惠清,顾浩声.软土地区土钉墙现场试验及土钉结构的稳定性分析[J].岩石力学与工程学报,2011,30(5):1065-1072.YING Hui-qing,GU Hao-sheng.Field test on soil nails and stability analysis of soil-nailing retaining structure in soft soil area[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(5):1065-1072.
[3]张晃,郑俊杰,辛凯.土钉支护技术在软土基坑中的应用[J].岩石力学与工程学报,2002,21(6):923-925.ZHANG Zhao,ZHENG Jun-jie,XIN Kai.Application of soil nail technique in soft soil foundation pit[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(6):923-925.
[4]罗桂红.土钉墙在温州软土基坑工程中的应用[J].土工基础,2006,20(3):4-6.LUO Gui-hong.Application of soil nailing wall method in pit engineering of soft clay area in Wenzhou City[J].Soil Engineering and Foundation,2006,20(3):4-6.
[5]清华大学土木系,总参工程兵科研三所.CECS96-97基坑土钉支护技术规程[S].北京:中国计划出版社,1997.
[6]山东省建设厅.GB50497-2009 建筑基坑工程监测技术规范[S].北京:中国计划出版社,2009.
[7]张明聚,郭忠贤.土钉支护工作性能的现场测试研究[J].岩土工程学报,2001,23(3):319-323.ZHANG Ming-ju,GUO Zhong-xian.Research on behaviors of soil nailing by field test[J].Chinese Journal of Geotechnical Engineering,2001,23(3):319-323.
[8]张凡,段建立,谭跃虎.复合土钉支护工作性能的现场测试研究[J].建筑技术,2003,34(2):104-105.ZHANG Fan,DUAN Jian-li,TAN Yue-hu.Site test and study on the shoring performance of composite soil nailing[J].Architecture Technology,2003,34(2):104-105.
