基于非线性响应的结构损伤识别响应面方法研究

徐亚兰，薛 敏

(西安电子科技大学 机电工程学院，西安 710071)

结构损伤识别作为结构健康监测技术的重要组成部分，一直是国内外学者研究的热点问题。结构损伤识别研究具有很强的工程背景，在土木工程、航空航天、机械工程等领域都有广泛的应用。结构损伤识别的方法很多，如振动诊断法、声发射法、超声波诊断法、光学诊断法、红外诊断法等。近年来，由于计算机技术、信号检测与处理技术的快速发展，基于振动信息的结构损伤识别方法的研究与应用最为广泛［1-2］。不过，虽然经过国内外学者的长期研究，基于振动信息的结构损伤识别已经形成很多方法［3-5］，如:动力指纹类方法、信号处理类方法，但是作为结构健康监测的一部分，结构损伤识别往往存在在线实时的要求［6］，而目前现有的损伤识别方法由于存在计算效率低、测量数据多等局限而不易于工程实际应用。

Box等［7］提出的实验设计与数理统计相结合的响应面方法，由于有高效、实用的特点，近年来在多个领域受到越来越多的重视。响应面方法在结构工程领域的应用主要集中在可靠性分析［8］及模型修正［9-10］等方面，而在结构损伤识别方面，特别是非线性损伤识别的应用研究鲜有报道。由于响应面模型有着较低的试验数据训练要求、计算量小、操作性强及非线性建模的优势，符合结构在线损伤识别的要求，显示了其在结构损伤识别领域的应用潜力。文献［11-12］尝试着将响应面方法应用于结构损伤识别中，建立了结构损伤与模态频率之间的近似解析表达式。

本文主要利用响应面方法在非线性建模问题上的优势，基于结构的非响应信号，提出以结构响应信号的功率谱特征量为损伤动力指标，建立结构非线性损伤与动力指标的响应面模型，探索性地研究响应面方法在结构非线性损伤中的应用。

1 非线性损伤的动力指标

结构发生损伤后，某些损伤行为会使结构的响应信号表现为非线性特性。尽管模态频率由于易测量且测试精度较高经常用来作为结构线性损伤识别的动力指标，但是模态频率在损伤定位方面有其局限性，而且利用固有频率很难对线性损伤与非线性损伤进行区分。考虑到与结构模态频率相比，响应信号频谱能量的分布对结构非线性特征更为敏感度，为了更好地描述非线性损伤造成结构响应信号频率能量特征的变化，本文提出以结构在冲击激励下响应信号的功率谱特征值作为损伤动力指标:

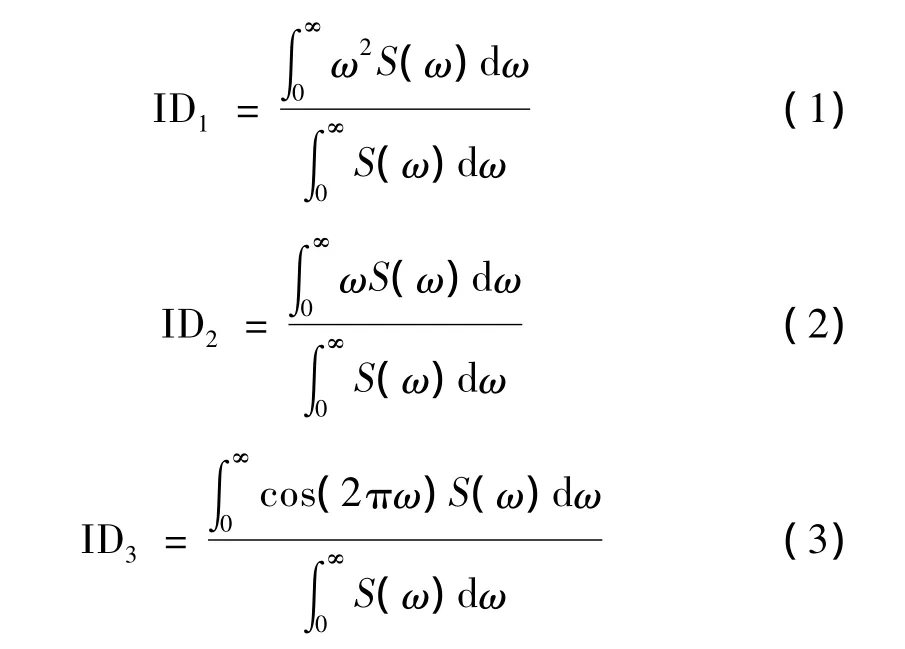
式中，S(ω)为结构响应信号的功率谱，ω为角频率。ID1，ID2，ID3能分别从不同的角度描述响应信号的频域特征，反映了其功率谱主频带位置和频谱能量分布的分散程度，其中，ID1表示功率谱主频带的位置，ID2表示信号功率谱的质心，ID3表示功率谱主频带的移动趋势。

2 响应面方法

响应面方法就是利用试验设计与回归分析方法，通过近似构造一个具有明确表达式形式的多项式对试验样本的回归进行拟合来表达隐式功能函数。试验样本的选取直接关系到响应面模型的精度与计算成本;样本选取过少不能完全反应系统的特征，而样本选取太多虽然能在一定程度上提高拟合精度，但会大幅度提高计算成本。在实际应用中样本选取主要取决于研究对象、特征量的选择以及所采用的试验设计方法。

试验设计是为了通过合理布置试验点的位置，达到利用少量试验点得到较高精度响应面模型的目的。试验设计的方法主要有全因子设计、部分因子设计、中心复合设计及Plackett-Burman设计等。本文在结构非线性损伤识别中将采用全因子设计方法和如下多项式响应面模型:

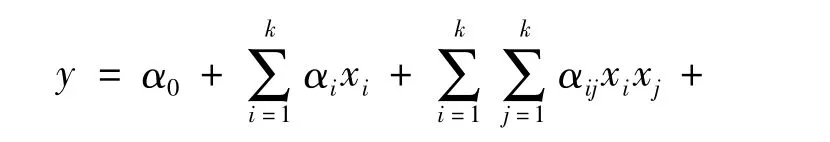
式中，xi(i=1，2，…，k)，y分别为响应面模型的输入参数和输出响应，k表示设计变量个数，α0是常数项待定系数，αj是一次待定系数，αij为二次项待定系数，αijm为三次项待定系数。全因子设计是最基本的试验设计方法，其将设计变量各分量上、下限之间的区域分成若干子区间，在各个子区间的交界处取值;若设计变量个数为n，每个设计变量分量均取l个值，则全因子设计试验点的个数为ln。

响应面函数对试验数据的拟和程度由如下评价指标来检验，即修正的负相关系数复相关系数R2adj和均方误差MSE:

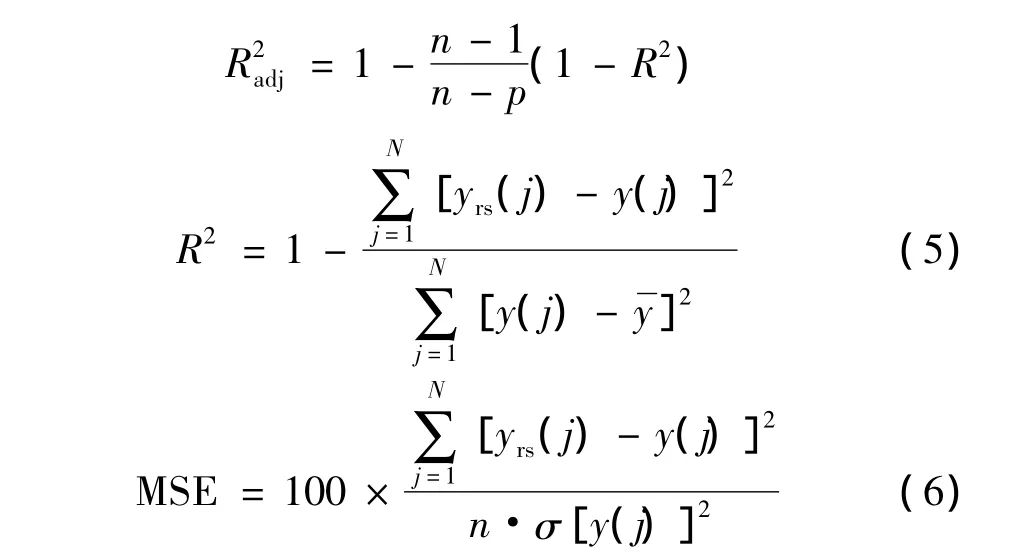
式中，yrs为响应面模型的计算值，y为真值为真值的均值，N为样本点的个数，n表示试验运行的次数，p为在输入量和输出量个数之和的基础上加一，为σ真值的标准偏差。值越接近1说明回归模型越准确，而MSE值越小说明拟合度就越好。

3 基于响应面方法的结构非线性损伤识别

基于响应面的结构损伤识别方法就是通过实验或数值计算获得输入变量及响应变量的样本点，利用多项式响应面方法对这些采样点进行拟合或逼近获得系统损伤与动力指标之间的近似解析表达式，将响应面思想引入结构损伤识别中，降低数据测试要求并提高计算效率，以便应用于在线结构健康监测。主要步骤包括试验所需要输入量与输出量的确定，基于试验设计的样本选取，响应面模型的建立以及利用响应面进行损伤识别。

为了验证本文所提出以功率谱特征量为损伤动力指标，利用响应面方法进行结构非线性损伤识别的有效性。本节对一个五自由度系统(如图1所示)的线性损伤和非线性损伤识别进行了仿真比较研究。这里，以各个弹簧刚度系数的变化来模拟结构的损伤，故损伤识别的目标就是弹簧的刚度值及其定位。利用全因子设计方法来建立刚度值、刚度定位与损伤动力指标ID1，ID2，ID3之间的拟合关系。因为损伤识别的目标就是弹簧的刚度值及其定位，故在实验设计时变量个数为2;每个变量均取5个设计水平，即:损伤定位分别为第1个弹簧至第5个弹簧，而五个定位中某一定位的损伤用弹簧刚度系数的降低来模拟，共分为五个等级(2 000 N/m，3 000 N/m，4 000 N/m，5 000 N/m ，6 000 N/m(健康值))。由于使用全因子设计需要25次仿真试验获得样本点，所以本文模拟仿真了25个不同的损伤工况。

仿真分为两种情况，首先，在非线性损伤发生后，仍将以线性动力学建模的方式产生试验样本点，即:分三步进行计算:① 针对各损伤工况，通过振型叠加，计算对应的响应;② 计算响应的功率谱;③ 利用第1至3式计算ID1，ID2，ID3。利用响应面方法分别拟合线性损伤及非线性损伤情况下刚度值及定位与ID1，ID2，ID3之间的解析关系如下:

其中，sti为刚度值，loc代表定位，L表示线性，NL表示非线性，A，B 和 C 分别表示 ID1，ID2，ID3。

图2与3分别为利用以上响应面模型对两种损伤情况下的刚度值和定位进行识别。从图可见，对非线性系损伤刚度值及定位的识别精确度总体上要比线性高，特别是对非线性损伤定位的识别基本上都在理想值(45°斜线)附近，而对线性损伤定位识别则比较分散，可见利用本文方法可以将线性损伤与非线性损伤进行区分。本文所采用功率谱特征值作为损伤动力指纹对线性损伤识别并不理想，线性损伤识别时采用结构的模态频率作为损伤指标比较准确［11］。

图2 线性损伤与非线性损伤刚度值的识别结果Fig.2 Stiffness results for linear and nonlinear damage

然后，假设已知系统发生的损伤为非线性，以系统非线性动力学建模的方式来产生试验样本点，即:在计算系统响应时，针对各个发生非线性损伤的弹簧，用非线性项kx3替代原线性项kx，利用Newmark数值解法获得近似的响应。建立非线性损伤情况下刚度值及定位与ID1，ID2，ID3之间的解析关系如下:

图4和图5为采用非线性动力学模型进行非线性损伤定位和刚度值的识别结果。可以看出，响应面模型可以对非线性损伤进行定量与定位识别。与图2和图3进行比较可知，试验样本点的准确度可以很大程度上提高非线性损伤识别的响应面方法的准确度。

4 结论

图3 线性损伤与非线性损伤定位的识别结果Fig.3 Location results for linear and nonlinear damage

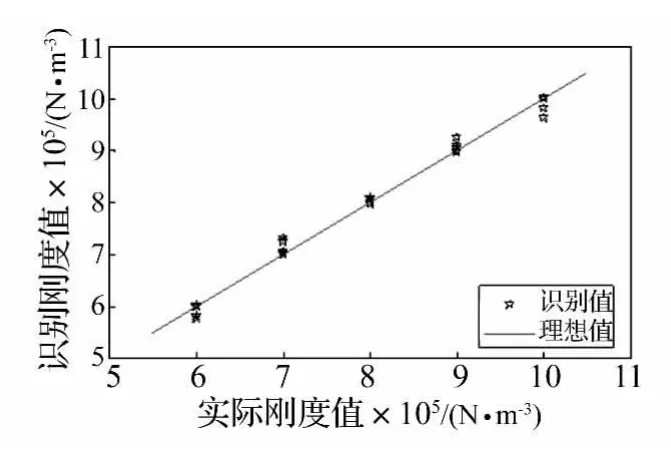
图4 非线性损伤刚度值的识别结果Fig.4 Stiffness results for nonlinear damage

图5 非线性损伤定位的识别结果Fig.5 Location results for nonlinear damage

本文提出了一种以结构响应信号的功率谱特征值为损伤动力指标，探索性地将响应面方法用于对结构的非线性损伤识别的方法，并与结构的线性损伤识别进行了比较研究。结果表明，本文所提出的方法可以将结构的线性损伤与结构的非线性损伤很好的区分开来，对结构的非线性损伤有很好的定位和定量精度。由于响应面方法可以在很少的测试数据情况下，快速准确地建立结构非线性损伤与损伤动力指标之间的关系，显示了其在结构非线性损伤识别领域的应用潜力。

［1］杨秋伟.基于振动的结构损伤识别方法研究进展［J］.振动与冲击，2007，26(10):86-89.YANG Qiu-weiA review ofvibration based structural structural damage identification methods［J］.Journal of Vibration and Shock，2007，26(10):86-89.

［2］ Yan Y J，Cheng L，Wu Z Y，et al.Development in vibration-based structural damage detection technique［J］.Mechanical Systems and Signal Processing，2007，21(5):2198-2211.

［3］Shiradhonkar S R，Shrikhande M.Seismic damage detection in a building frame via finite element model updating［J］.Computers and Structures，2011，89:2425-2438.

［4］ Law S S，Li X Y，Zhu X Q，et al.Structural damage detection from wavelet packet sensitivity［J］.Journal of Sound and Vibration，2004，278:589-610.

［5］严平，李胡生，葛继平，等.基于模态应变能和小波变换的结构损伤识别研究［J］.振动与冲击，2012，31(1):361-366.

YAN Ping，LI Hu-sheng，GE Ji-ping，et al.Structural damage identification based on modal strain energy and wavelet transformation［J］.Journal of Vibration and Shock，2012，31(1):361-366.

［6］杨智春，于哲峰.结构健康监测中的损伤检测技术研究进展［J］.力学进展，2004，34(2):215-225.

YANG Zhi-chun，YU Zhe-feng.Progress of damage detection for structural health monitoring［J］.Advances In Mechanics，2004，34(2):2155-225.

［7］ Box G P，Wilson K B.On the experimental attainment of optimum conditions［J］.Journal of Royal Statistical Series B，1951，13:1-51.

［8］胡冉，李典庆，周创兵，等.基于随机响应面法的结构可靠度分析［J］.工程力学，2010，27(9):192-199.

HU Ran， LIDian-qing， ZHOU Chuang-bing， etal.Structural reliability analysis using stochastic response surface method［J］.Engineering Mechanics，2010，27(9):192-199.

［9］Ren Wei-xin，Chen Hua-bing.Finite element model updating in structural dynamics by using the response surface method［J］.Engineering Structures，2010，32:2455-2465.

［10］韩芳，钟冬望，龚相超.基于信息融合技术的结构模型修正研究［J］.固体力学学报，2011，32:421-426.

HAN Fang， ZHONG Dong-wang， GONGXiang-chao .Research on model updating based on information fusion［J］.Chinese Journal of Solid Mechanics，2011，32:421-426.

［11］ Cundy L A.Use of response surface metamodels in damage identification of dynamic structures［D］. Virginia，Ploytechnic institute and state university，2002.

［12］Fang S E，Perera R.Damage identification by response surface based model updating using D-optimal design［J］.Mechanical Systems and Signal Processing，2011，25:717-733.