基于动载试验的板桥检测及性能分析

王兆斌

(山西省孝义市公路管理段，山西孝义032300)

随着我国国民经济的快速发展，公路货运量大幅增长，交通流密度及车辆载重越来越大，致使部分公路桥梁不满足使用要求，制约了社会经济的发展［1］.桥梁结构的动力荷载试验是评判桥梁承载能力和运营状况的有效手段之一［2］.桥梁动力荷载试验基于结构固有模态参数的检测，分析桥梁结构自振特性和车辆动力荷载与桥梁结构联合振动特性，可较准确计算出桥梁现状结构安全状况和承载能力，为公路桥梁的运营养护管理提供重要理论依据［3-6］.以动力荷载的试验方法对山西省某八跨简支预应力空心板梁桥实体检测，分析其整体动力性能，对提高桥梁的安全性具有重要现实意义.

1 工程概况

该桥建于1995年4月，桥梁全长143 m，上部结构为八跨简支预应力空心板，横向分布13块板，每跨桥长16 m.桥面宽度净15 m(行车道)+2×0.5 m(护栏)，桥宽16 m.下部结构为桩柱式桥墩，基础桥台为重力式桥台.设计荷载:公路－Ⅰ级.

2 动载试验

桥梁动力荷载试验是指桥梁在实际的动荷载作用下，测定桥梁结构振幅、动应力、加速度以及冲击系数等动力响应，这些参数反映了桥梁结构在动荷载作用下的受力状态及动力作用对驾驶员、乘客及行人舒适性的影响.把实测数据信号进行处理分析，可揭示桥梁结构振动的内在规律，综合评价桥梁结构的动力性能.

2.1 动载试验设计

根据实地交通调查，结合常规检查及无损检测结果，选择确定该桥第三跨作为检测桥跨进行动力荷载试验.动载试验工况见表1，传感器测点布置如图1所示.

表1 动载试验工况表

图1 第三跨传感器测点布置(单位:cm)

1)脉动试验

脉动试验是指桥梁只受环境和大地激励下产生微弱振动，通过桥上布置的高灵敏度传感器记录桥梁的振动情况，经动力分析计算出结构的竖向自振频率.

2)跑车试验

跑车试验是指试验车以不同行驶速度通过桥梁，使桥梁结构产生不同程度的强迫振动，车辆产生的激振力频率会与桥梁结构的某阶固有频率比较接近，桥梁结构在该频率下会产生共振现象，此时桥梁各部位的振动响应达到最大.在车辆驶离桥跨后，桥梁作自由衰减振动，通过检测的波形曲线得到桥梁的动力特性.试验载重汽车在工况二、三下分别以20 km/h、30 km/h的车速匀速驶过桥梁，以测定桥梁在不同行车速度下试验截面的动力响应时程曲线.跑车试验实景图如图2所示.

图2 跑车试验实景

2.2 冲击系数的确定

动荷载冲击系数是指结构的动挠度与静挠度的比值.挠度反映了桥跨结构的整体变形，是衡量结构刚度的主要指标，因此活载冲击系数综合反映了荷载对桥梁的动力作用.通过工况二、三跑车试验记录的跨中挠度时程曲线等数据，冲击系数可由式(1)计算得到:

式中:Ydmax为动载作用下该测点最大挠度值，即最大波峰值;Ydmean为相应的静载作用下该测点最大挠度值，其值可由动挠度曲线求得(即本次波形的振幅中心轨迹线顶点值)，公式为

式中:Ydmax为动载作用下该测点最大挠度值，即最大波峰值;Ydmin为动载作用下相应的最小挠度值，即同周期波谷值.

3 试验数据分析

3.1 脉动试验

脉动试验中传感器采集的测点数据时程曲线见图3，频率计算结果如图4所示.

由图3可见该桥平均脉动加速度为0.013 mm/s2，在81 s时加速度达最大值0.14 mm/s2，表明该桥自身振动情况较小.通过对图3所示的测点加速度时程曲线进行傅里叶变换，得到各个测点的位移功率谱，并对其宽带随机响应相关分析得到相关功率谱，进行谱分析，并通过模态识别分析得到图4所示的试验桥跨实测竖向一阶频率图.

图3 脉动试验测点加速度时程曲线

图4 脉动试验测点傅里叶变换频率

当外界环境和大地对桥梁产生的振动频率与结构的固有频率接近时，结构此时的振幅达到最大值，振幅最大波峰处的频率即可视为结构的固有频率.从图4可知，该桥在振幅达最大值0.25 mm时对应的频率即为该桥的固有频率8.326 Hz.该桥理论一阶频率为4.822 Hz，自振频率实测值均大于理论值，根据规范［7］要求，该桥在外界自然因素作用下不会产生共振，桥梁结构整体动刚度处于较好状态，有较强的抗冲击性能，结构动力特性能满足设计要求.

3.2 跑车试验

20 km/h跑车试验采集的动挠度时程曲线见图5，频率计算结果如图6所示.

图5 20 km/h跑车试验动挠度时程曲线

30 km/h跑车试验采集的动挠度时程曲线见图7，频率计算结果如图8所示.

根据冲击系数的计算方法，该桥冲击系数计算结果见表2.

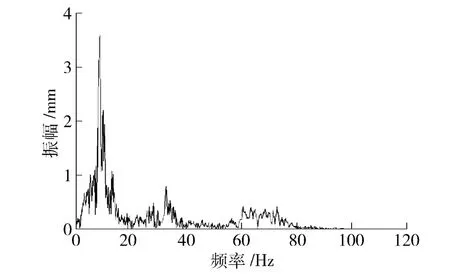
图6 20 km/h跑车试验频率计算结果

图7 30 km/h跑车试验动挠度时程曲线

图8 30 km/h跑车试验频率计算结果

表2 跑车试验结果表

根据跑车试验采集的动挠度时程曲线图5、7可知，该桥在364 s时动挠度达到最大值0.29 mm，此时车辆运行速度为30 km/h.把跑车条件下测点的动挠度时程曲线经傅里叶变换，得到该桥在20、30 km/h车速下桥梁频率在9.2～9.7 Hz之间.该桥理论一阶频率为4.822 Hz，跑车条件下该桥频率实测值均大于理论值，表明该桥结构在车辆荷载作用下出现共振的几率很小.根据冲击系数的计算方法可得该桥动力增大系数在1.376～1.386之间，冲击系数在行车速度为30 km/h时达最大值0.386，规范［7］规定，该桥冲击系数满足使用要求，表明桥梁自身动力特性较好，有较强的抗冲击性能，车辆动荷载对该桥的动态影响较小.

4 结论

通过采用动力荷载试验法对山西省某预应力空心板简支梁大桥进行了实地动力荷载检测试验，把采集的测点时程曲线等试验数据运用傅里叶变换分析法进行分析，得到该桥竖向一阶频率为8.326 Hz，自振频率实测值大于理论值4.822 Hz，表明桥梁结构整体刚度满足设计要求，具有一定的安全储备;通过工况二、三的跑车试验，得到该桥在跑车条件下的频率值和冲击系数，并分析出该桥在行车速度为30 km/h时冲击系数达最大值0.386，满足规范要求，说明该桥的动力特性较好，有较强的抗冲击性能，为桥梁安全研究提供了一种新的思路.

［1］张英兰.桥梁动载试验的作用与发展前景［J］.公路，2002(9):32-35.

［2］王自彬，岳渠德，赵金环，等.动力荷载试验在桥梁检测评估中的应用［J］.青岛理工大学学报，2007，28(1):14-16.

［3］李国豪.桥梁结构稳定与振动［M］.中国铁道出版社，1992(10):265-268.

［4］欧阳政伟，余志武，蒋丽忠，等.异型钢一预应力混凝土叠合板组合箱梁桥成桥试验［J］.长沙铁道学院学报，2003，21(2):50-55.

［5］MAECK J，ABDEL W M，PEARTERS B，et al.Damage identification in reinforced concrete.Structures by Dynamic Stiffness Determination［J］.Engineering Structures，2000，22(10):1339-1349.

［6］宋一凡.公路桥梁荷载试验与结构评定［M］.北京:人民交通出版社，2002.

［7］中华人民共和国交通部.公路桥涵设计通用规范(JTG D60—2004)［S］.北京:人民交通出版社，2004.