加筋土边坡地震稳定性动点安全系数分析方法

董士杰，魏红卫

（中南大学 土木工程学院，长沙 410075）

1 引言

地震作用下的边坡稳定性分析主要有拟静力法、时程分析法两类。在实际工程中，由于缺少足够的工程经验和地震灾害资料，目前仍旧以拟静力法的计算结果作为工程抗震设计的依据。但是拟静力法没有考虑地震的震动特性和边坡自身的动力特性，而是将动力反应简化为静力求解，所以拟静力法不能准确地描述地震发生时边坡随时间变化的实际情况。地震作用下边坡的动力响应问题，可以对边坡加速度时程、速度时程、位移时程和应力时程等动力特性进行分析。王环玲等[1]的研究表明，用时程分析法计算边坡在地震作用下的动力响应问题能够真实地反应出边坡的动态特征。由于边坡稳定性在地震作用下表现出的是一个动态过程，所以选取一个具有实际物理意义的安全系数评价指标来表征边坡的地震稳定性十分重要。现有的岩土体边坡动力安全系数时程分析方法主要分为3步：确定边坡潜在滑裂面；动力分析得到潜在滑裂面位置的岩、土体单元的动力特性，将动力场施加到初始应力场并按照静力方法计算出边坡的动安全系数时程；根据所得到的动安全系数时程计算出一个定值来评价地震作用下岩土体边坡的稳定性。

郑颖人等[2–3]提出基于拉-剪破裂面动力时程分析法和强度折减动力分析法；刘建军等[4]提出了地震荷载下岩质边坡动安全系数评价方法；刘汉龙等[5]从概率分析和能量的角度出发，提出了边坡地震稳定性时程分析方法，并以最小平均安全系数作为评价指标。这些方法在岩土体边坡的动力稳定性分析中具有很高的参考价值，但对于加筋土边坡，由于其设置了筋材，边坡的内部结构复杂[6]，地震作用下对滑裂面搜索也更加困难，所以对于加筋土边坡的地震稳定性分析，需要综合有效的时程分析方法。

杨涛等[7]提出了根据边坡潜在失稳滑面上的正应力和滑动方向的剪应力来定义安全系数，即点安全系数；杨果林等[8]将点安全系数法运用到静力作用下加筋挡墙的安全系数计算上，推导出静力作用下基于FLAC3d的加筋挡墙点安全系数的计算方法；蒋青青[9]研究了基于Hock-Brown准则点安全系数的边坡稳定性分析。由于点安全系数法能够表征复杂工程内部不同结构和部位的稳定性状态，在边坡、隧道等较复杂工程领域内的适用性已经得到了肯定。对于加筋土边坡，点安全系数法可以分别运用到边坡的土体、筋材和筋-土界面的安全性评价上，通过综合分析加筋-土边坡内部不同结构的稳定性，为加筋土边坡的稳定性分析提供了一种新的思路。

本文将点安全系数进行推广，运用到加筋土边坡的动力稳定性分析中，提出了一种水平地震和竖直地震共同作用下基于安全储备意义的土工合成材料加筋土边坡的动点安全系数时程分析方法，并简要对比分析了水平地震和竖直地震对动点安全系数的影响。

2 动点安全系数定义

定义材料的安全系数为一定条件下材料的屈服强度与其实际的力学状态的比值：

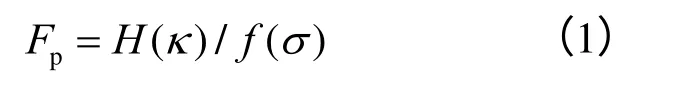
式中：f为关于材料应力σ的函数关系；Н为内变量为κ的材料参数，安全系数Fp为材料的安全储备系数。

对于土工合成材料的加筋土边坡，进行数值计算时，将边坡模型不同结构分别离散为土体单元、土工合成材料筋材单元和筋-土界面单元。从土体单元弹塑性破坏安全储备、筋材单元抗拉安全储备和筋-土界面单元抗剪切破坏安全储备3个方面定义边坡的安全系数，由得到的岩土体安全系数时程、筋材安全系数时程和筋-土界面安全系数时程分别对时间加权求得平均值得到3个定值，并以最小值作为加筋土边坡整体在地震作用下的动点安全系数。计算过程中，记录动力特性相关数据的时间间隔约为10-5s，为了避免由于应力集中或者数值误差引起的安全系数不合理突变，取每0.1 s的动力特性均值进行安全系数的计算，以确保动点安全系数的有效性。

2.1 岩土体安全系数时程

为了更好地分析加筋土边坡的地震稳定特性，设定加筋土边坡的土体为均质土，土体单元采用理想弹塑性本构模型以及摩尔-库仑屈服准则，屈服函数表示为

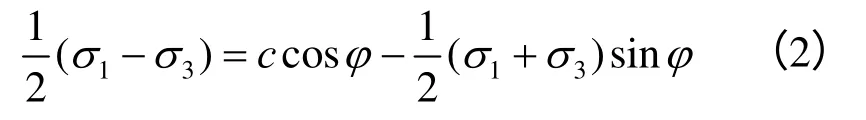
式中：σ1、σ2和σ3是土体单元动力作用下的主应力；c为黏聚力；φ为内摩擦角。由式（2）可得t 时刻加筋土边坡土体单元i 的安全储备系数表达式为

取边坡所有土体单元在t 时刻的最小值为该时刻边坡土体的动点安全系数：

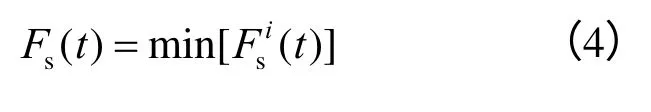
2.2 土工合成材料安全系数时程

设定土工合成材料为土工格栅，能够承受很大拉力而不能承受压力的薄膜材料。Radoslaw[10]研究了地震作用下加筋土坡的稳定性，认为在竖直地震荷载下，加筋土边坡中的筋材会受到非常大的拉力，所以在水平和竖直地震共同作用下，很有必要着重考虑筋材的抗拉稳定性。采用geogrid单元模拟土工合成材料，geogrid单元为各向正交异性的线弹性材料，内嵌于土体单元并与土体单元发生直接的剪切和摩擦作用。当筋材承受轴向拉力作用时，筋材单元j 在t 时刻的安全储备系数表示为

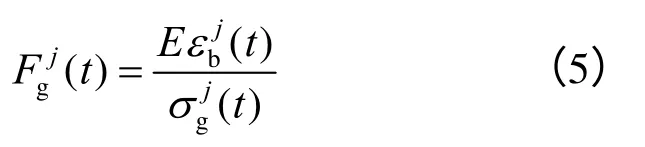
式中：εb为筋材单元的抗拉应变；σg为筋材单元收到的拉应力；E为筋材单元的拉伸模量。取所有筋材单元在t 时刻的最小值作为该时刻边坡筋材的动点安全系数：

1.推行青年干部历练制度。目前新录用的青年干部由于业务不够熟悉，给税收管理带来很大的困难。因此要大力推行青年干部历练制度，通过多岗位锻炼，培养青年干部工作技能，激励青年干部勇挑重担，多干事、能干事、干成事，不断提高工作效率和执法水平。

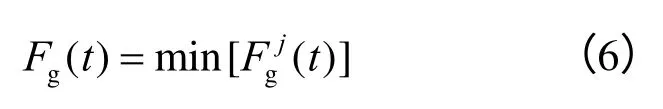
2.3 筋-土界面安全系数时程

在土工合成材料加筋土边坡中，筋材和岩土体的接触面上的剪切方向的界面强度由摩擦特性控制，摩擦特性由筋材的耦合弹簧中单位面积上耦合弹簧刚度、耦合弹簧黏结强度和耦合弹簧摩擦角，以及有效侧限应力共同决定。

式中：σm为有效侧限应力；σn为筋-土界面单元法向应力；p为孔隙压力。

根据摩擦加筋机制，加筋土边坡中，筋材通过筋-土界面与边坡的土体发生摩擦咬合作用，这种相互作用使边坡的土体稳定性增加。根据加筋机制，设定筋-土界面发生剪切破坏，屈服准则采用摩尔-库仑屈服准则，得出t 时刻筋-土界面单元k 的点安全系数 Ff(t) ：

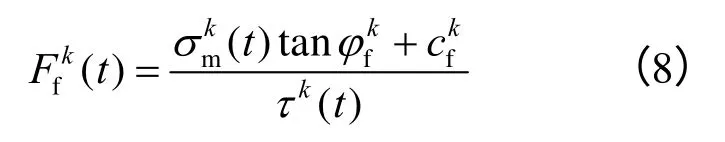
式中：φf为界面单元的耦合弹簧摩擦角；cf为界面单元的耦合弹簧黏聚力。取所有筋-土界面单元在t时刻的最小值作为该时刻边坡界面单元的动点安全系数：

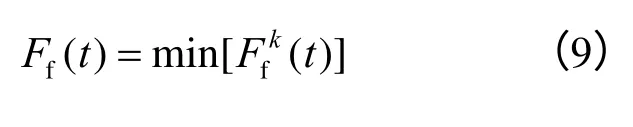
2.4 加筋土边坡动点安全系数

定义边坡土体、筋材和筋-土界面的动点安全系数为安全系数时程对时间加权的平均值：

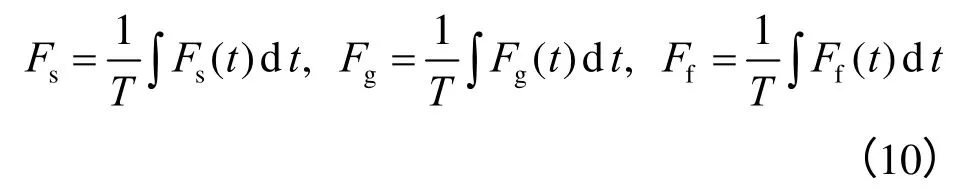
式中：T为地震荷载作用的时间。

同时，定义加筋土边坡动点安全系数为

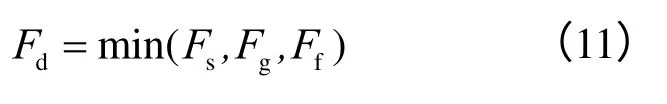
3 算例分析

3.1 模型概况

对模型施加动力荷载，会使模型边界上存在动力波的反射，对分析的结果造成影响，边界越大，对动力波的反射产生的影响越小。但是，设置非常大的边界会使建立的模型变得很大，严重降低了计算效率。通过设置黏滞性边界，既可以有效减少边界对波的反射所产生的影响，又大大缩短了动力计算的耗时。在商业软件Flac3d中建立加筋土边坡模型以及边界条件，如图1所示，有限差分模型如图2所示。

图1 数值模型Fig.1 Numerical model

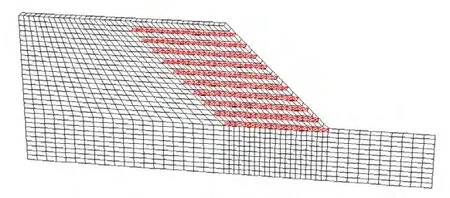
图2 有限差分模型Fig.2 Finite difference model

设定边坡高度为10 m，地基为5 m，坡顶长度为20 m，坡度为1∶1，地基长度为40 m；筋材长度为10 m，铺设10层，相邻两层竖直间距为1 m，土体和筋材参数见表1和2。

表1 土体力学参数Table 1 Mechanical parameters of soil

表2 土工格栅力学参数Table 2 Mechanical parameters of geogrid

对数值模型采用瑞利阻尼进行动力计算，首先对模型进行无阻尼动力计算，得到坡顶某监测点x方向的速度-时程曲线如图3所示，可以确定该模型的最小中心频率fmin约为28.3 Hz。由于边坡是岩土体材料，所以设定临界阻尼比为5%[11]。

图3 加筋土边坡速度-时程曲线Fig.3 Velocity time-history curve of reinforced soil slope

3.2 地震荷载

地震荷载采用EL-centro波的前30 s，水平方向采用EL-centro地震波的N-S方向数据，竖直方向采用EL-centro地震波UP方向数据。地震波加速度-时程曲线如图4所示。在输入地震波前，需要对地震波加速度时程曲线进行基线校准，由校准后的地震波速度-时程转化为应力-时程作为输入的地震波荷载[12]。

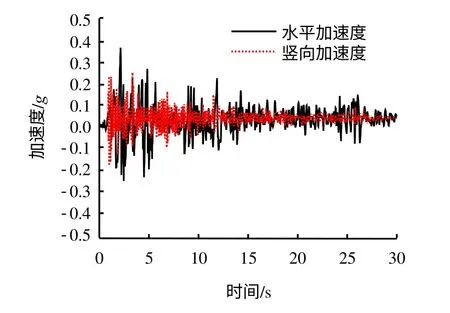
图4 地震波加速度-时程曲线Fig.4 Acceleration time-history curve of seismic wave

具体计算过程如下：①对模型进行静力计算至平衡；②施加构造应力场，并以模型此时的应力状态作地震作用下为动力分析的初始应力状态；③动力计算，计算过程中使用FISH语言开发的工具对模型的动力特性进行检测和记录，并编译数据处理程序对所得到的数据进行计算，得到加筋土边坡在地震作用下的动点安全系数；④存储相关数据。

4 结果和分析

4.1 加筋土边坡稳定性分析

动力计算得到的土体、筋材和筋-土界面单元的动点安全系数-时程曲线见图5。按照式（10）将3个安全系数-时程函数分别对时间加权求平均值，得到：土体动点平均安全系数Fs=1.69；筋材动点平均安全系数Fg=4.30；界面单元动点平均安全系数Ff=3.81。最后按照式（11）得到地震作用下土工合成材料加筋土边坡的安全系数Fd=1.69。

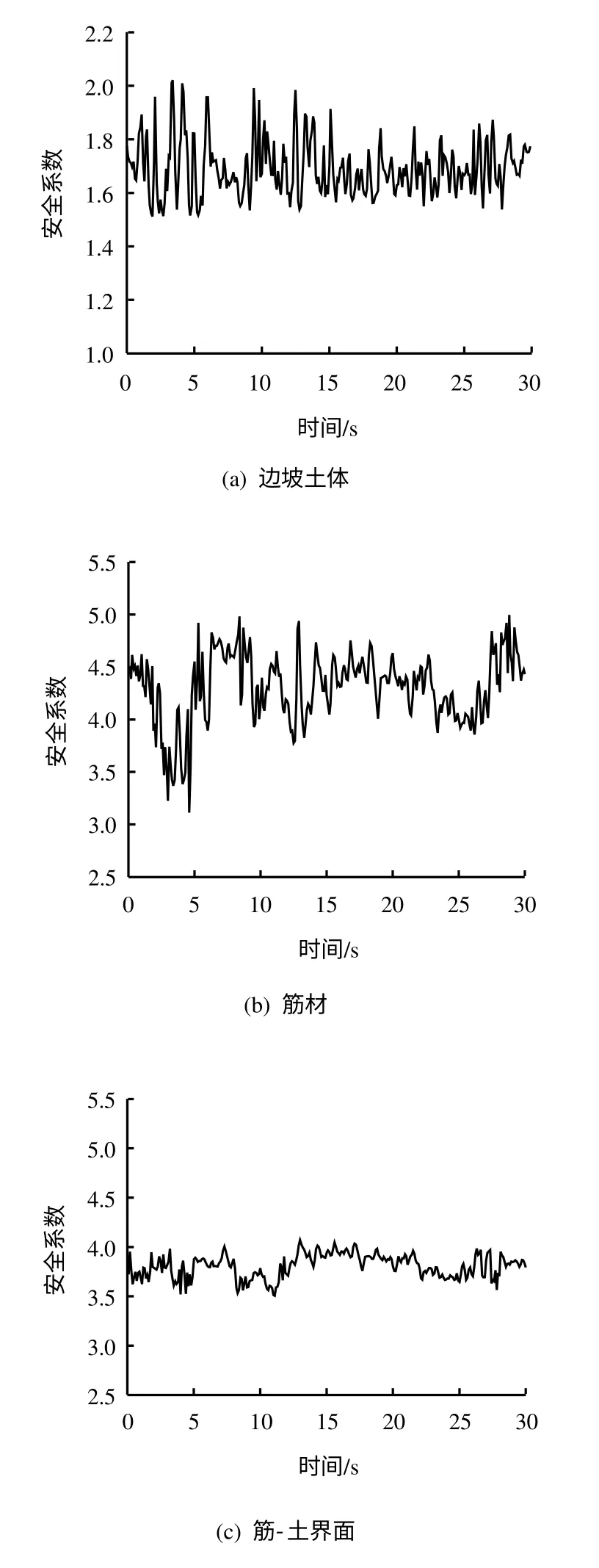
图5 安全系数-时程曲线Fig.5 Curves of safety factor time-history

采用极限平衡原理的拟静力法计算上述模型得到的安全系数为1.74，采用强度折减法动力分析方法计算上诉模型得到的安全系数为1.77，与动点安全系数所得的1.69比较一致，验证了动点安全系数分析方法的合理性。动点安全系数从加筋土边坡的土体、筋材和筋-土界面3个方面分别计算安全系数，并且取三者最小值作为加筋土边坡的地震稳定性评价指标，既符合有限单元动力时程分析方法的要求，又使加筋土边坡工程的地震稳定性分析更加全面。以动点安全系数作为指标，可以为边坡工程的加筋抗震设计提供一定的参考价值。

4.2 水平和竖直方向地震对比分析

将El-centro地震波中的水平（NS）和竖直方向（UP）的地震荷载分别加载到模型上，并计算加筋土边坡的动点安全系数如表3所示。

表3 不同方向地震作用下加筋土边坡动点安全系数Table 3 Dynamic point safety factor of the slope under horizontal and vertical seismic actions

水平方向地震对加筋土边坡的整体动点安全系数影响比竖直方向地震约大7.69%，对边坡土体的动点安全系数影响比竖直方向大7.69%；对于筋材的动点安全系数，竖直方向的地震影响比水平方向地震影响大9.07%，对于筋-土界面的动点安全系数，竖直方向的地震比水平方向大13.9%。结果说明，对于加筋土边坡，水平地震比竖直地震对边坡土体的稳定性影响更大，同时也对加筋土边坡稳定性影响更大；竖直地震的作用比水平地震对筋材和筋-土界面的稳定性影响更大，计算结果符合Radoslaw的研究成果，证明了动点安全系数的正确性。

5 结论

（1）动点安全系数是具有实际物理意义的评价指标，并且具有合理的数据处理方法。

（2）动点安全系数采用完全动力的分析方法，为复杂的加筋土边坡工程的动力分析提供了一个综合的计算方法，体现出加筋土边坡工程中的比较薄弱的结构，对于边坡抗震设计具有一定的参考价值。

（3）水平方向地震对加筋土边坡整体的稳定性影响更大，而竖向地震对加筋土边坡中筋材的抗拉稳定性和筋-土界面的抗剪稳定性影响更大。

[1] 王环玲, 徐卫亚. 高烈度区水电工程岩石高边坡三维地震动力响应分析[J]. 岩石力学与工程学报, 2005,24(增刊l):5890－5895.WANG Huan-ling, XU Wei-ya. 3D dynamical response analysis of high rock slope related to hydropower project in high intensive seismic region[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Supp.l):5890－5895.

[2] 郑颖人, 叶海林, 黄润秋, 等. 边坡地震稳定性分析探讨[J]. 地震工程与工程振动,2010,30(2):173－180.ZHENG Ying-ren, YE Hai-lin, HUANG Run-qiu, et al.Study on the seismic stability analysis of a slope[J].Journal of Earthquake Engineering and Engineering Vibration,2010,30(2):173－180.

[3] 郑颖人, 叶海林, 黄润秋. 地震边坡破坏机制及其破裂面的分析探讨[J]. 岩石力学与工程学报, 2009, 28(8):1714－1723.ZHENG Ying-ren,YE Hai-lin,HUANG Run-qiu.Analysis and discussion of failure mechanism and fracture surface of slope under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1714－1723.

[4] 刘建军, 李跃明, 车爱兰. 地震载荷下岩质边坡动安全系数评价[J]. 应用力学学报,2011,28(6):595－601.LIU Jian-jun, LI Yue-ming, CHE Ai-lan. The evaluation for dynamic safety coefficient of rock slope under seismic loading[J].Chinese Journal of Applied Mechanics,2011,28(6):595－601.

[5] 刘汉龙, 费康, 高玉峰. 边坡地震稳定性时程分析方法[J]. 岩土力学,2003,24(4):553－560.LIU Han-long, FEI Kang, GAO Yu-feng. Time history analysis method of slope seismic stability[J]. Rock and Soil Mechanics,2003,24(4):553－560.

[6] 张兴强, 闫澍旺, 陈文金. 土工格栅与土动力相互作用的有限元分析[J]. 天津大学学报,2001,34(4):525－528.ZHANG Xing-qiang, YAN Shu-wang, CHEN Wen-jin.FEM analysis on dynamic soil-geogrid interaction[J].Journal of Tianjin University,2001,34(4):525－528.

[7] 杨涛, 周德培, 马惠民, 等. 滑坡稳定性分析的点安全系数法[J]. 岩土力学,2010,31(3):971－975.YANG Tao, ZHOU De-pei, MA Hui-min, et al. Point safety factor method for stability analysis of landslide[J].Rock and Soil Mechanics,2010,31(3):971－975.

[8]杨果林，刘泽.加筋土挡墙稳定性分析的点安全系数法[J].中南大学学报(自然科学版)，2012，43(5):1908－1913.YANG Guo-lin，LIU Ze.Point safety method for stability analysis of reinforced earth retaining wall[J].Journal of Central South University:Science and Technology，2012，43(5):1908－1913.

[9][9]蒋青青.基于Hock-Brown准则点安全系数的边坡稳定性分析[J].中南大学学报:自然科学版，2009，40(3):786－790.

JIANG Qing-qing.Stability of point safety factor of slope based on Hoek-Brown criterion[J].Journal of Central South University:Science and Technology，2009，40(3):786－790.

[10]RADOSLAW L M.Soil reinforcement for seismic design of geotechnical structures[J].Computers and Geotechnics，1998，23(1):1－17.

[11][11]刘春玲，祁生文，童立强，等.利用FLAC3D分析某边坡地震稳定性[J].岩石力学与工程学报，2004，23(16):2730－2733.LIU Chun-ling，QI Sheng-wen，TONG Li-qiang，et al.Stability analysis of slope under earthquake with FLAC3D[J].Chinese Journal of Rock Mechanics and Engineering，2004，23(16):2730－2733.

[12]陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:中国水利水电出版社，2009.