基于熵值—灰色关联分析模型的产业结构转换能力评价

岳斯玮

(重庆商务职业学院公共管理系, 重庆 401331)

基于熵值—灰色关联分析模型的产业结构转换能力评价

岳斯玮

(重庆商务职业学院公共管理系, 重庆 401331)

从产业结构转换能力的概念及其影响因素出发, 构建了产业结构转换能力的评价指标体系, 在此基础上提出了基于熵值法和灰色关联分析法的熵值——灰色关联综合评价模型.该模型不仅将产业结构转换视为灰色系统, 而且考虑了评价指标与评价对象之间的相互联系, 并且运用该模型对西部具有代表性7省的产业结构转换能力进行了综合评价, 得到其产业结构转换能力的排序, 充分证明了指标体系和评价模型的有效性和可实践性.

熵值法；灰色关联分析法；产业结构转换能力；评价指标体系；西部7省

1 引言

对于经济的发展, 除了注重速度外, 还更应该注重质量.因此, 一个区域要保持经济持续快速的发展, 除了要加大经济资源的开发投资外, 更重要的是产业结构的调整.只有通过推进区域产业结构合理化和高度化来寻求速度和效益, 才能实现经济又好又快的发展.产业结构调整的关键是产业结构的转换, 所谓产业结构的转换是指一个国家或地区国民经济各部分及整个产业结构随主导产业更替而发生的质的变化[1-2].而产业结构的这种适应市场变化和保持区域经济持续、快速发展, 向高级化调整、演进的可能性和条件, 则为产业结构转化能力[3-4].因此, 一个地区产业结构的转换能力决定了区域经济增长的速度和效果, 所以研究区域产业结构转换能力, 有助于了解区域产业结构所处的水平、相对变动和发展潜力, 进而分区域析产业结构的现实情况, 对正确调整产业结构, 促进产业结构的优化升级, 从而提高区域经济发展水平有着重要意义.

目前, 众多学者在产业结构的转换能力的评价中多采用层次分析法、主成分分析法.层次分析法容易受主观意识和判断的影响, 而根据产业结构转换能力的概念可知, 影响产业结构转换能力的因素太多, 在其评价时只能选择主要指标, 而这些指标中, 有些是定性的, 有些是定量的, 因此具有灰色特征[5].但是, 目前在产业结构的转换能力的评价中采用灰色分析法较少.不过灰色关联分析法在计算关联系数时采用均值加权的方式, 而产业结构转换能力的评价指标中各指标的权重一般是不一样的.因此, 本文针对产业结构转换能力概念和目前的评价现状, 以及灰色关联分析法的特点, 采用熵值法对评价指标加权, 构建熵值——灰色关联分析综合评价模型, 对区域产业结构转换能力进行客观评价.

2 区域产业结构转换能力评价指标体系

产业结构转换能力的优劣, 反映了区域产业结构的综合水平与潜力, 对区域经济的持续、快速、健康发展有着重要作用.而影响区域产业结构转换能力的因素较多, 但根据这些因素的特点, 可以将其概况为以下主要几个方面[6,7]: 创新能力、需求因素、供给因素、结构因素、对外贸易、政策因素.并且产业结构转换能力是一个综合概念, 任何一个单一指标都不能将其概括.所以, 根据产业结构转换能力的概念以及影响产业结构转换能力的因素, 构建了区域产业结构转换能力的评价指标体系, 具体见表1.

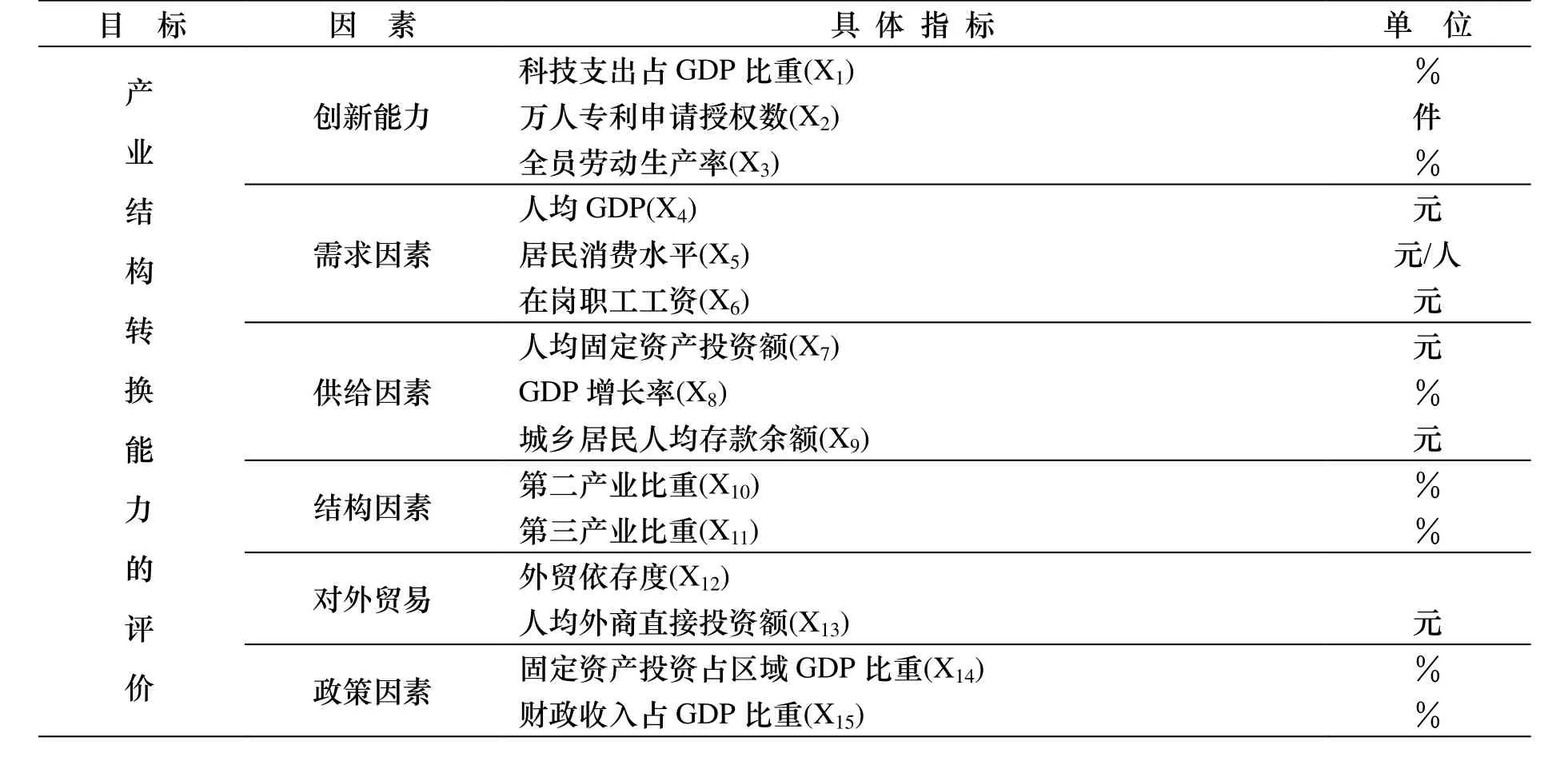
表1 产业结构转换能力的评价指标体系Table 1 The industrial structure conversion capability evaluation index system

3 评价模型的构建

根据熵值法和灰色关联分析法构建熵值——灰色关联分析综合评价模型, 对区域的产业结构转换能力进行评价.该模型首先利用熵值法得到区域产业结构转换能力评价指标体系中各指标的权重, 然后利用灰色关联分析法确定各评价指标的灰色关联系数.在此基础上, 计算评价对象的加权灰色关联系数, 从而来测度评价对象的产业结构转换能力水平.

3.1 熵值法原理

在信息论中, 信息熵是系统无序程度的度量, 信息量越大, 不确定性就越小, 熵也就越小；信息量越小, 不确定性越大, 熵也越大.根据熵的特性, 通过计算指标的信息熵, 根据指标的相对变化程度对系统整体的影响来确定指标的权重, 这种方法为熵值法[8,9].因此熵值法是一种客观赋权方法, 可以为多指标的综合评价提供很好的客观评价依据.假设某评价系统包括m个评价对象, 每个评价对象有n个评价指标, 从而构成一个m×n的原始评价矩阵A, 其中元素为第i个评价对象在第j个指标上的指标值, 则熵值法确定指标权重的步骤如下:

1)为了消除量纲对评价结果的影响对各指标进行标准化处理, 得到各指标的标准化值, 标准化的公式如下[10]:

对于正向指标:

对于负向指标:

由于, 在熵值的计算时需要取对数, 因此指标值必须为正数, 所以如果标准化后的值若为0, 则对该指标值进行平移, 其公式为:

2)计算第j个指标下第 i 个评价对象指标值的比重, 得到矩阵P, 其中元素为[11]:

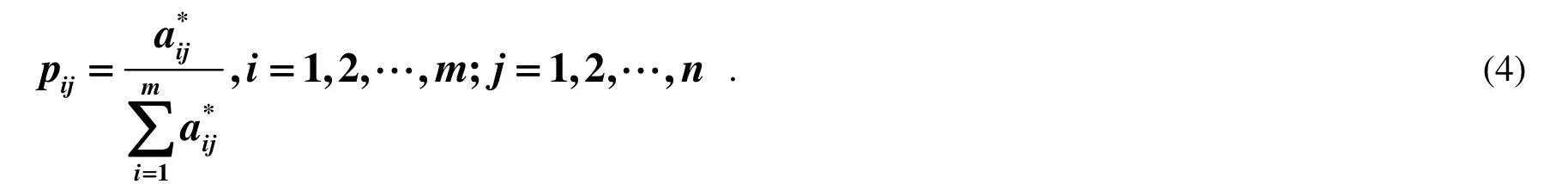
3)计算第j项指标的熵值:

4)计算第j项指标的差异系数[11]:

5)计算第j项指标的熵值权重系数:

3.2 熵值—灰色关联分析综合评价模型

1982年, 邓聚龙教授提出灰色系统理论, 该理论中的灰色关联分析法可以定量分析两个因素之间的相互关联的程度, 该分析法的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密.曲线越接近, 相应序列之间的关联度就越大, 反之就越小[12].但是, 在计算关联程度时, 灰色关联理论是取关联系数的算术平均值为关联度, 这种方法要求同层各属性重要程度差异不大.然而, 产业结构转换能力的综合评价涉及指标不仅多, 而且各指标之间是存在客观联系的, 对产业结构转换能力的重要程度通常是不一样的.因此, 必须区分各指标的计算权重乘以关联系数得到加权关联度.

所以, 基于以上考虑, 根据熵值法、灰色关联分析法的原理, 构建了熵值——灰色关联分析综合评价模型,具体步骤如下:

1)设m个评价对象, 有n个评价指标, 建立原始评价矩阵:

2)确定参考序列:

3)数据的标准化处理:

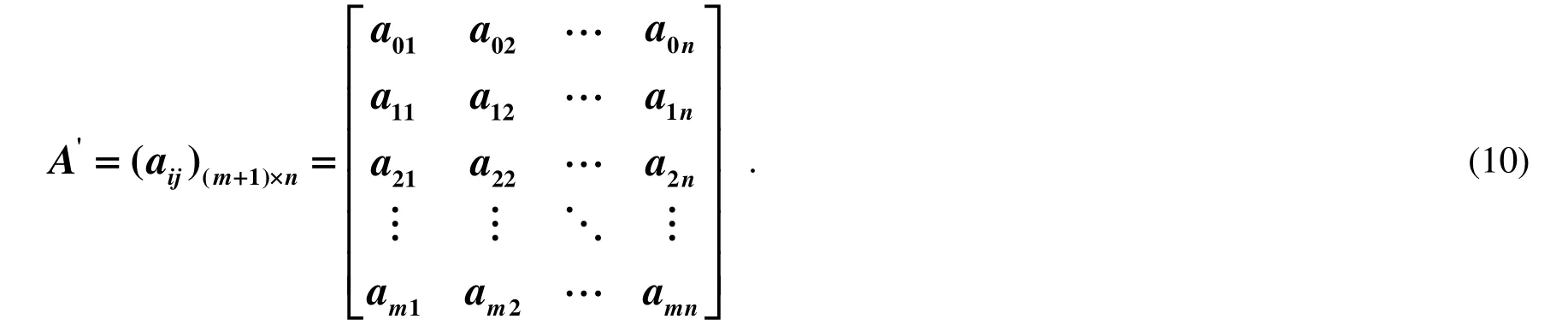
由参考序列和原始评价矩阵组成评价增广矩阵:

4)计算关联系数:

根据灰色关联分析法原理可知, 计算关联系数的公式为[13,14]:

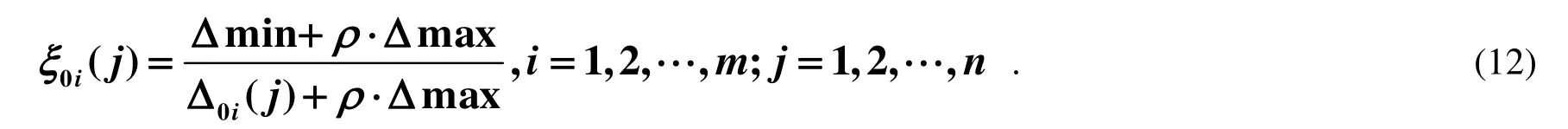
5)计算熵值权重向量:

根据熵值法的原理, 利用熵值权重系数的计算公式(7), 计算出各指标的权重系数, 从而得到总的权重向量为:

6)综合评价

根据熵值权重向量, 计算得出各评价对象的熵值灰色关联向量, 具体的计算公式为[15,16]:

熵值灰色关联向量中各分量的值为各评价对象的熵值灰色关联系数, 并且关联度系数的值即为各评价对象的产业结构转换能力水平, 从而根据熵值灰色关联向量就可以对参评对象的产业结构转换能力水平进行综合评价.

4 实证分析

4.1 研究样本和数据选择

由于四川、重庆、云南、广西、陕西、内蒙古、新疆等这7个省份的发展在西部具有重要地位, 他们的经济发展模式对整个西部的发展来说具有示范性作用, 直接关系到整个西部的建设, 从而影响到全国经济的发展水平.并且, 这些省份中有很多是资源性城市, 随着资源的开发利用, 必将面临产业结构的的转变问题, 这是实现经济持续发展的必然要求.因此, 选择四川、重庆、云南、广西、陕西、内蒙古、新疆等7个西部具有代表性的省作为研究对象.另外, 为了了解这7个省份的产业结构转换能力在全国的地位, 从而推断出西部的产业结构转换能力水平, 将全国的产业结构转换能力也作为一个评价对象.

产业结构转换能力评价指标体系中各指标的数据来源于2009年至2012年四川、重庆、云南、广西、陕西、内蒙古、新疆等7个省的统计年鉴和中国统计年鉴.评价年限之所以选择2009年至2012年, 这主要是综合以下因素的选择:

1)根据中国现行的统计制度, 年度数据更具规范性和准确性, 因此选择年度数据进行产业结构转换能力的评价更具精确性和操作性；

2)由于统计数据的公布具体延迟性, 因此2009年至2012年是目前公布的数据最全面的4个年度, 且最接近目前的经济水平, 从而数据更具说服力；

3)产业结构转变是连续和稳定的, 因此选择4年的数据, 应能反映当前区域的产业结构转换能力水平.

4.2 西部7省产业结构调整能力的综合评价

根据前文建立的熵值——灰色关联分析综合评价模型, 以2012年为例, 对西部7个具有代表性的省份的产业结构转换能力进行评价, 具体过程如下:

4.2.1 构建产业结构转换能力评价增广矩阵

按照熵值——灰色关联分析综合评价模型的步骤1), 根据产业结构转换能力的评价指标体系, 查找和计算出2012年西部7省和全国产业结构转换能力指标数据值, 得到原始评价矩阵；在此基础上, 根据综合评价模型的步骤2), 确定各指标值的最优值, 得到参考序列；从而得到产业结构转换能力评价增广矩阵, 具体见表2.

表2 2012年西部代表性7省的产业结构转换能力评价增广矩阵Table 2 Industrial structure typical conversion capability assessment augmented matrix in 7 provinces of western 2012

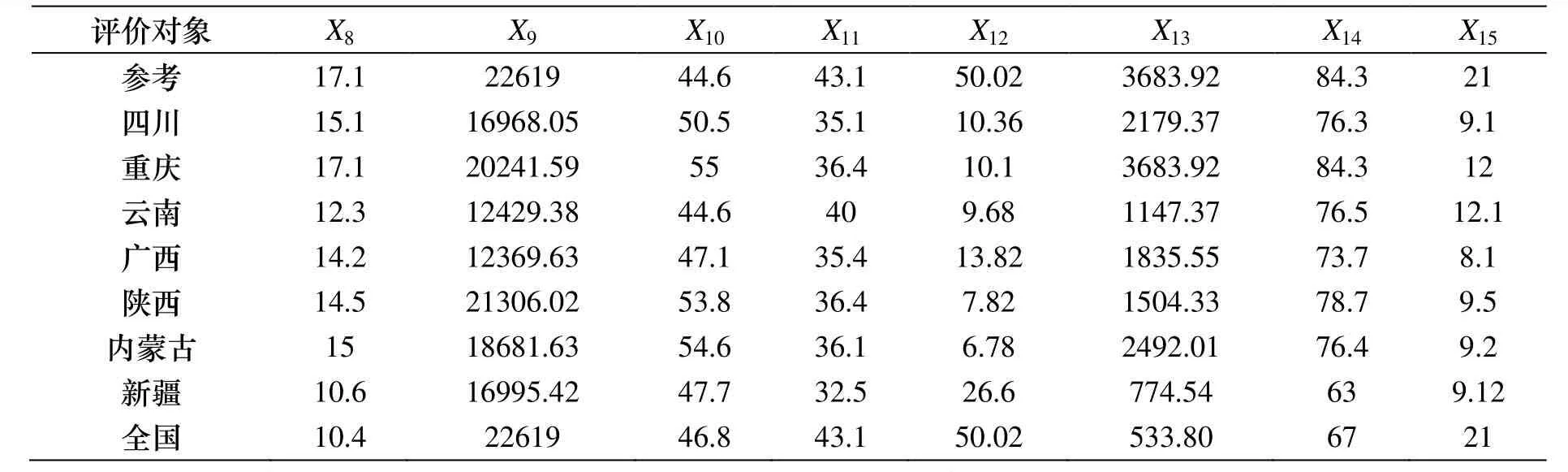
续表2 2012年西部代表性7省的产业结构转换能力评价增广矩阵Table 2 Industrial structure typical conversion capability assessment augmented matrix in 7 provinces of western 2012

按照熵值——灰色关联分析综合评价模型的步骤3), 为了避免各指标量纲的影响, 需对各指标的值进行标准化处理.根据评价指标的建立过程知指标X10为负向指标, 其余为正向指标, 因此根据标准化公式(1)和(2)对各指标进行标准化处理, 得到标准化的增广矩阵, 具体见表3.

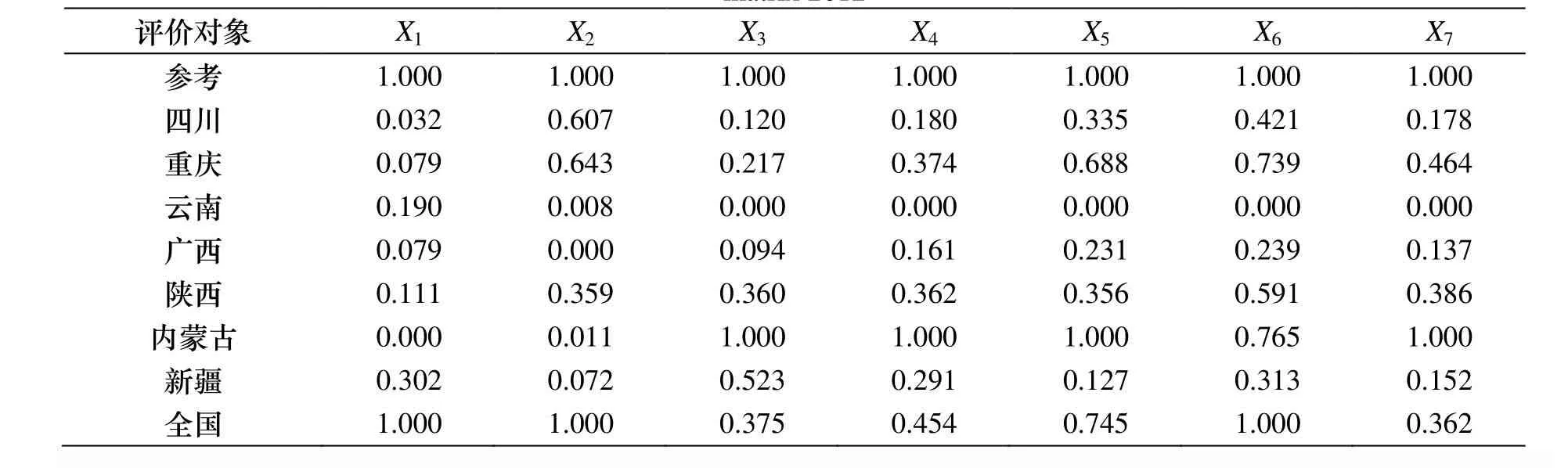
表3 2012年西部代表性7省的产业结构转换能力标准化评价增广矩阵Table 3 Representative seven provinces in western industrial structure transformation ability of standardized assessment augmented matrix 2012

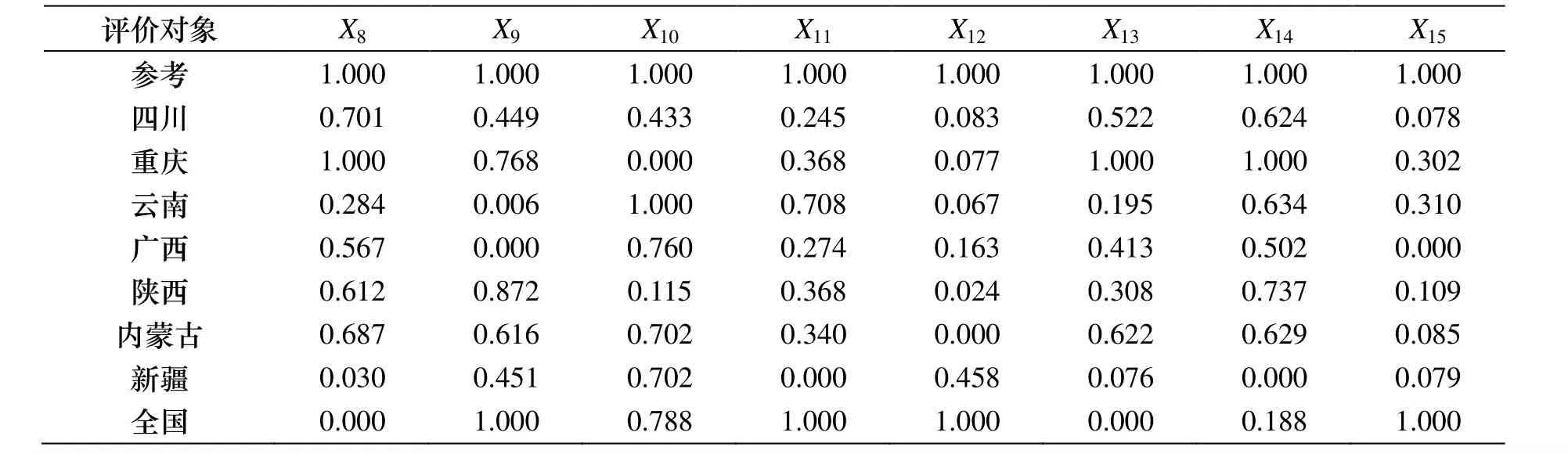
续表3 2012年西部代表性7省的产业结构转换能力标准化评价增广矩阵Table 3 Representative seven provinces in western industrial structure transformation ability of standardized assessment augmented matrix 2012

4.2.2 关联度系数矩阵的测算

按照熵值——灰色关联分析综合评价模型的步骤4), 根据标准化后的评价增广矩阵, 利用公式(12)计算出各指标的关联系数, 得到关联系数矩阵, 具体见表4.

表4 2012年西部代表性7省的产业结构转换能力关联系数矩阵(Table 4 Representative seven provinces in western industrial structure correlation coefficient matrix switching capability 2012()

表4 2012年西部代表性7省的产业结构转换能力关联系数矩阵(Table 4 Representative seven provinces in western industrial structure correlation coefficient matrix switching capability 2012()

评价对象 X1X2X3X4X5X6X7四川 0.341 0.560 0.362 0.379 0.429 0.463 0.378重庆 0.352 0.583 0.390 0.444 0.616 0.657 0.482云南 0.382 0.335 0.333 0.333 0.333 0.333 0.333广西 0.352 0.333 0.356 0.373 0.394 0.396 0.367陕西 0.360 0.438 0.438 0.439 0.437 0.550 0.449内蒙古 0.333 0.336 1.000 1.000 1.000 0.680 1.000新疆 0.417 0.350 0.512 0.414 0.364 0.421 0.371全国 1.000 1.000 0.444 0.478 0.662 1.000 0.439

续表4 2012年西部代表性7省的产业结构转换能力关联系数矩阵()Table 4 Representative seven provinces in western industrial structure correlation coefficient matrix switching capability 2012()

续表4 2012年西部代表性7省的产业结构转换能力关联系数矩阵()Table 4 Representative seven provinces in western industrial structure correlation coefficient matrix switching capability 2012()

评价对象 X8X9X10X11X12X13X14X15四川 0.626 0.476 0.468 0.398 0.353 0.511 0.571 0.351重庆 1.000 0.683 0.333 0.442 0.351 1.000 1.000 0.417云南 0.411 0.335 1.000 0.631 0.349 0.383 0.577 0.420

广西 0.536 0.333 0.675 0.408 0.374 0.460 0.501 0.333陕西 0.563 0.796 0.361 0.442 0.339 0.419 0.655 0.359内蒙古 0.615 0.566 0.627 0.431 0.333 0.569 0.574 0.353新疆 0.340 0.477 0.627 0.333 0.480 0.351 0.333 0.352全国 0.333 1.000 0.703 1.000 1.000 0.333 0.381 1.000

4.2.3 指标熵值权重的测算

按照熵值——灰色关联分析综合评价模型步骤5), 利用2012年这7个评价省份产业结构转换能力评价指标体系中各指标的具体数据, 根据熵值法的步骤计算出产业转换能力评价指标体系中15个指标的熵值权重, 从而得到熵值权重向量:

W=(0.1171, 0.1069, 0.0652, 0.0518, 0.0520, 0.0383, 0.0604, 0.0525, 0.0545, 0.0401, 0.0437, 0.1255, 0.0563, 0.0346, 0.1012)

4.2.4 产业结构调整能力综合评价值的测算

按照熵值——灰色关联分析综合评价模型步骤6), 根据公式(15)计算得出熵值灰色关联向量, 即2012年西部代表性7省以及全国的产业结构转换能力的综合评价值.类似地, 可以计算出2009年到2011年的产业结构转换能力的综合评价值, 具体见表5.

表5 2009年—2012年西部代表性7省的产业结构转换能力综合评价Table 5 Industrial Structure Transfer Capability Evaluation representative seven provinces in western 2009-2012

5 结论

针对产业结构转换能力的评价现状, 从产业结构转换能力的概念及其影响因素出发, 在构建产业结构转换能力评价指标体系的基础上, 根据熵值法和灰色关联分析法构建了一个产业结构转换能力的综合评价模型.该模型通过熵值法确定评价指标的权重, 从而以熵值灰色关联度作为判定评价对象优劣的准则.该模型不仅将产业结构的转换视为灰色系统, 而且考虑到了产业结构转换能力评价指标之间以及评价对象之间的客观联系, 因此使得评价结果更符合实际, 从而有很强的现实意义.并且利用该模型对西部代表性的7个省份的产业结构转换能力进行了应用验证, 所以该模型为产业结构的转换能力的评价提供了一种新的可操作的方法.下一步可以对西部这7省的产业结构转换能力的差异性进行评价分析.

[1]高洪深.区域经济学[M].北京: 中国人民大学出版社, 2002.

[2]秦寿康.综合评价原理与应用[M].北京: 电子工业出版社, 2003.

[3]芮明杰.产业经济学[M].上海: 上海财经大学出版社, 2005.

[4]白雪梅.中国区域经济的比较研究[M].北京: 中国财政经济出版社, 1998.

[5]张路蓬, 苏屹, 刘晓静.基于灰色关联的能源消耗与产业结构调整分析[J].统计与决策, 2011(15): 122-124.

[6]褚晓, 沙景华.西部五省产业结构转换能力比较分析[J].资源与产业, 2012,14(2): 27-32.

[7]罗吉.西部地区产业结构转换能力比较的实证研究[J].重庆大学学报, 2004(2): 11-14.

[8]王超, 田磊磊.济南市产业结构调整的灰色系统关联分析[J].经济研究导刊, 2010(25): 180-181.

[9]李占国, 高志刚.基于组合评价的中国区域产业结构转换能力研究[J].经济问题探索, 2007(8): 35-38.

[10]李生明, 葛岳静, 英丽娜.中国地级以上城市产业结构转化能力评价[J].资源与产业, 2010, 12(3): 59-62.

[11]郑宇, 董川顺,马登哲.基于AHP和熵值法的项目供应商灰色关联评价[J].工业工程与管理, 2011, 16(6): 66-68.

[12]刘思峰, 党耀国, 方志耕等.灰色系统理论及其应用[M].5版.北京: 科学出版社, 2010.

[13]韩延玲, 高志刚.新疆县域产业结构转换能力综合评价[J].地域研究与开发, 2006, 25(5): 24-28.

[14]邓聚龙.灰色系统基本方法[M].2版.武汉: 华中科技大学出版社, 2005.

[15]左鹏, 刘强.重庆市垫江县农业产业结构的灰色关联分析[J].重庆交通大学学报: 社科版, 2012, 12(1): 56-58.

[16]杨建仁, 刘卫东.基于灰色关联分析和层次分析法的新型工业化水平综合评价——以中部六省为例[J].数学的实践与认识, 2011, 41 (2): 122-132.

Evaluation of the transformation of the industrial structure ability based on the entropy method and gray relational analysis method

YUE Si-wei
(Chongqing Business Vocational College, Chongqing 401331, P.R.C.)

Based on the influence factors of the transformation of the industrial structure, this paper constructs the transformation of the industrial structure ability evaluation index system. This paper puts forward a method based on entropy and gray correlation analysis, gray relation entropy weight comprehensive evaluation model. This model not only regards the transformation of the industrial structure as a gray system, but also considers the evaluation index and evaluation of the relationship between objects, and uses the model in the 7 representative western provinces to carry on the comprehensive evaluation. It is fully proved that the index system and evaluation model is of validity and practicality.

entropy method; gray relation analysis；transformation of the industrial structure ability；evaluation index system；7 western provinces

F224

A

1003-4271(2014)06-0953-08

10.3969/j.issn.1003-4271.2014.06.27

2014-08-26

岳斯玮(1986-), 男, 汉族, 四川汉源人, 讲师, 硕士, 研究方向: 数理统计学理论与应用, E-mail:281693223@qq.com.

重庆市教育委员会科学技术研究项目(KJ100725)