基于ANSYS的V型发动机曲轴瞬态动力学分析

王 子，苏铁熊，王 军

（中北大学机械与动力工程学院，山西太原 030051）

基于ANSYS的V型发动机曲轴瞬态动力学分析

王 子，苏铁熊，王 军

（中北大学机械与动力工程学院，山西太原 030051）

对某V型发动机曲轴进行运动学分析，建立三维模型。然后根据有限元理论，应用ANSYS软件对曲轴进行瞬态动力学分析。分析一个循环内的应力云图和变形图，从结果可以看出，曲轴的应力集中在主轴颈过渡圆角处、连杆轴颈的过渡圆角处以及连杆轴颈上的油孔处附近。

发动机曲轴；ANSYS；瞬态动力学分析

0 前言

曲轴是发动机中所受载荷最大的零件之一。它承受着连杆力、旋转质量惯性力和往复惯性力，都是周期性变化的载荷。理论和实践表明，汽车发动机曲轴的破坏形式主要是扭转破坏和弯曲应力疲劳，因此曲轴受到的交变弯曲和扭转应力可能会引起曲轴疲劳失效并对其他零件带来破坏。因此，如何准确地计算出整体式多缸机曲轴的应力、变形的大小及疲劳寿命，对于曲轴的设计和改进具有指导作用。

针对连杆作用在曲轴上的载荷，运用有限元分析软件对载荷施加做了方法上的研究，并对瞬态结果下的应力进行了分析，为下一步的曲轴疲劳寿命预测研究奠定了基础。

1 瞬态动力学分析

瞬态动力学分析（即时间历程分析）是用于确定结构所受载荷随时间变化的动力响应的方法。瞬态动力学在分析求解中的基本运动方程为：

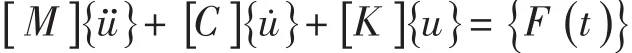
其中：

[M]为结构质量矩阵；

[C]为结构阻尼矩阵；

[K]为结构刚度矩阵；

{F(t)}为动载荷向量；

{u}为节点位移向量；

在任意给定的时间段内，这个方程都可以看做是考虑了一系列的惯性力[M]{u¨}和阻尼力[C] {u˙}的静力学平衡方程。这个方程的数值求解方法主要有直接积分法、振型迭代法和子空间迭代法三种方法。

据对速度和加速度等进行不同的假设，工程中已提出了很多种用直接积分法来求解动力学微分方程，这些方法在精度和适用性方面都各有优势。其中线性加速度法计算起来比较容易，但是对Δt/T的值必须限定范围，才能保证计算的稳定。此外经过多次计算表明，用线性加速度法得到的位移要比精确解偏大，而得到的速度则比精确解偏小。为了计算的精度和稳定性，提出了许多逐步积分法。如纽马克（Newmark）法和威尔逊θ（Wilson-θ）法，其中威尔逊θ法延伸了时间步τ=θ Δt(θ＞1.37)的范围，假定加速度按线性变化并进行逐步积分，证明了这种方法是无需边界条件的，即Δt/T的值没有范围限制，并可保证在数值积分计算时的稳定性。软件ANSYS中使用的是纽马克（Newmark）法，其也是按线性加速度的原理提出的一种逐步积分法，且威尔逊θ（Wil⁃son-θ）法原理类似[6]。

用Ansys做瞬态分析的过程主要有5个步骤：

（1）前处理（建立模型和划分网格）；

（2）施加边界条件；

（3）设定求解控制器；

（4）瞬态求解；

（5）后处理（观察结果）。

1.1 曲轴有限元模型的建立

由于多缸机曲轴结构复杂、单元数多，计算量大，所以取曲轴单拐进行计算。曲轴材料特性如表1所示。

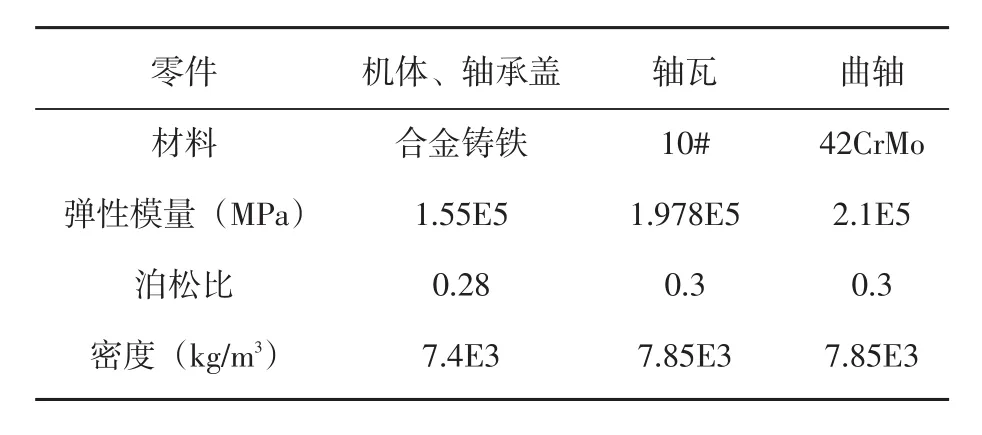
表1 曲轴组合各部分材料特性

在软件Pro/E中对曲轴进行实体建模。并将模型导人ANSA中进行自由网格划分。选取Solid185四面体单元离散模型，并对油孔处、连杆轴颈及主轴颈的过渡圆角处进行局部细化，以保证计算结果更准确。其中主轴颈和连杆轴颈处过渡圆角处选取单元尺寸为1 mm，主轴颈与连杆轴颈其他部分采用单元尺寸大小为2 mm，曲柄臂选取单元尺寸为4 mm，主轴承盖部分采用单元尺寸为10 mm。曲轴单拐组合三维网格模型如图1。

1.2 边界条件的施加

（1）约束边界条件的施加

对于曲轴-轴承盖组合结构，结合实际情况，首先将轴承盖上侧面全部约束UX、UY、UZ，两侧面施加X方向的对称约束，即约束UX。而考虑到施加载荷后曲轴的运动状况，为保证曲轴不会转动应在曲轴的主轴颈两端面施加绕Z轴的转向约束MZ，为了方便施加，在主轴颈端面中间的圆心处建立局部柱坐标系，通过该柱坐标施加约束MZ。曲轴的轴向要完全释放，轴承座与轴承盖建立了接触对，因此不需要建立位移约束。

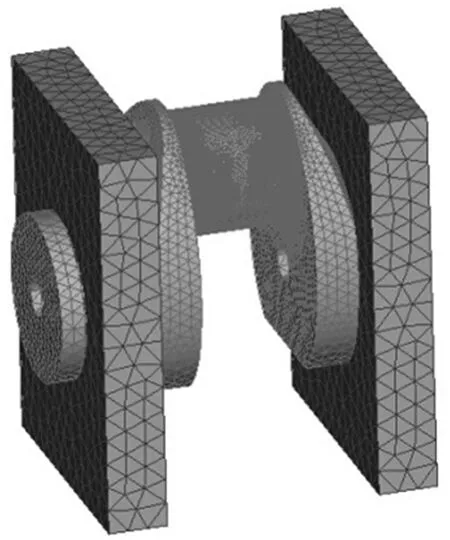
图1 曲轴组合三维模型

（2）接触边界条件的施加

通过有限元前处理软件ANSA对曲轴轴承组合建立了两个接触对：轴承座与轴承盖接触对，主轴颈与轴承座接触对。所有的接触对都需要对接触刚度进行定义，它决定了两个接触表面之间穿透量的大小。接触刚度选取太大，两个接触表面之间穿透量就越大，这就会引起总刚度矩阵的病态，造成计算的不收敛。一般来说，在选取足够大的接触刚度以保证接触穿透小到可以接受的同时，也要为了保证计算收敛考虑让接触刚度足够小。接触对之间的接触刚度FKN，一般取0.1到1中间的值，此处取FKN为0.1，因为较小的FKN有助于收敛。接触面之间的摩擦系数取材料间真实的摩擦系数值，此处为0.15。

（3）载荷边界条件的施加

根据传统的方法和连杆轴颈处油膜压力的分布规律，并忽略了油孔处应力集中的影响，可假设所加载荷是沿着曲柄销轴线的方向依照二次抛物线的规律分布的，范围是在圆周方向120°内按照余弦曲线的规律分布的，如图2所示。

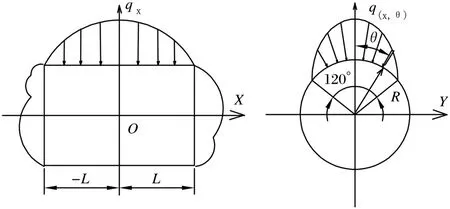
图2 力边界条件假定

沿曲轴轴线方向压力为：

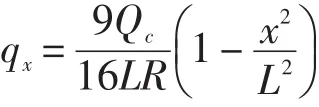
沿轴颈圆周方向的压力为：

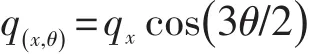
其中：Qc为作用在轴颈上的总载荷；x=-L～L；θ=-60°～60°。

针对16v396型柴油机的真实工作情况，此时柴油机只有曲柄传递爆发压力，所以要进行相应的改变，以符合真实的工作情况。由于此V型机曲轴上的一个曲柄销上连接两个连杆，且两连杆有90o夹角，因此在同一时刻曲柄销上的两个受力位置就会成的90o夹角。

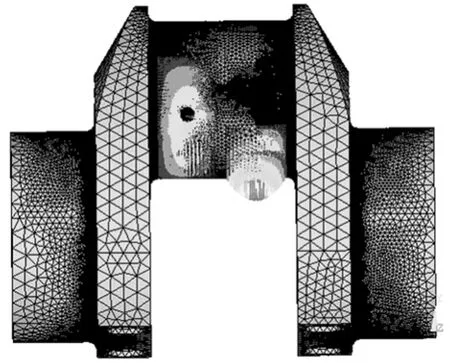
图3 施加载荷后的模型

对曲轴做瞬态分析前，载荷的施加有以下几个步骤：

（1）改变活动坐标系为局部圆柱坐标系；

（2）通过节点坐标R、θ、Z选取需要的节点，建立加载区域节点组；

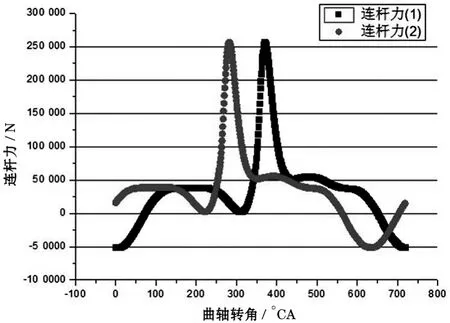
图4 载荷随曲轴转角的变化

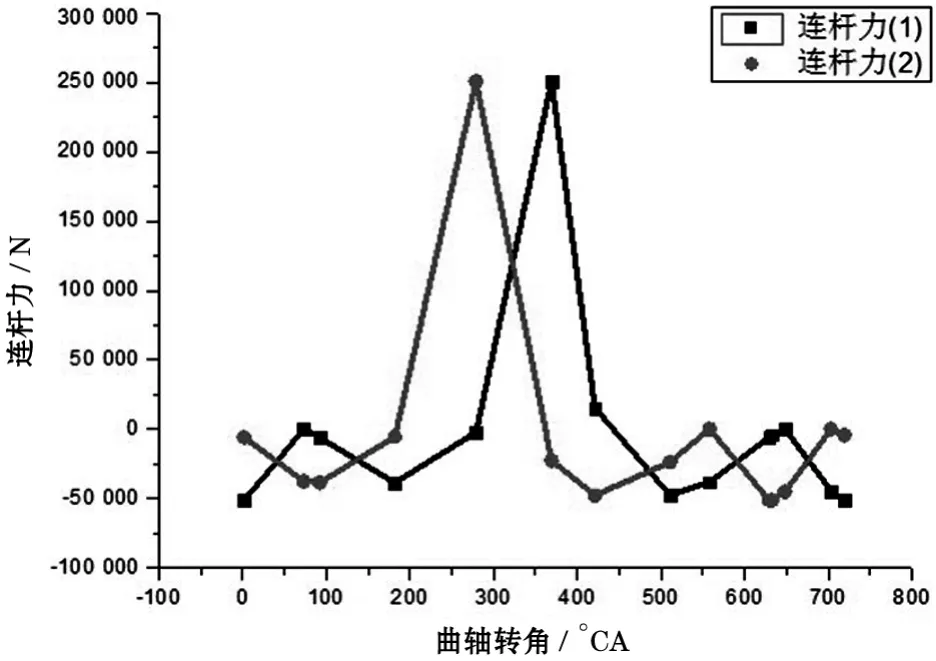
图5 一个循环内14个载荷随曲轴转角的变化

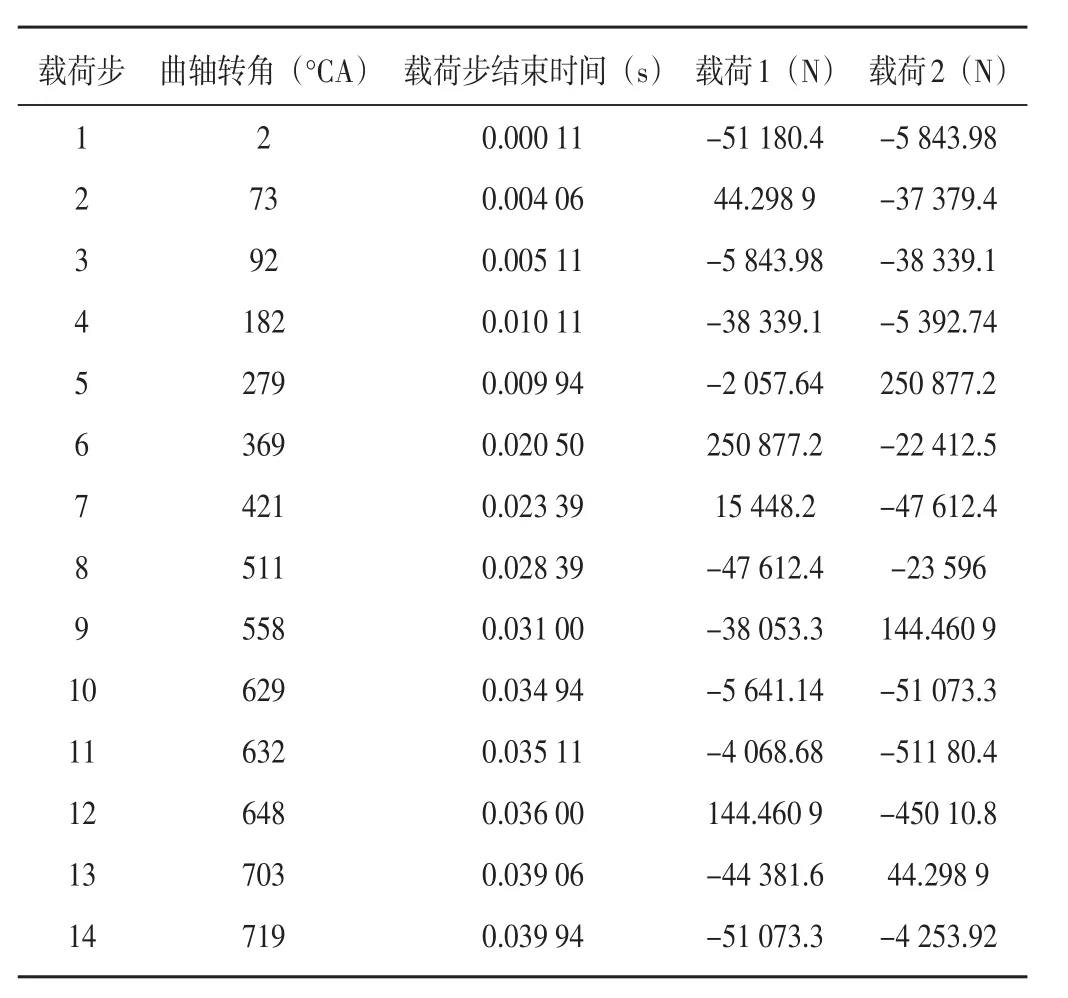
表1 载荷步设置

1.3 设置求解控制

曲轴动态响应分析是在转速为2 000 r/min（假设转速不变）的计算工况下进行的，完成一个工作循环所需时间大约为0.042 86 s。针对曲轴在一个工作循环受到的连杆作用力曲线，选取曲线的每一个波峰、波谷作为瞬态动力学分析的载荷步，这样就把每一个循环载荷都考虑进去了，载荷步选取的数量决定了与实际工作过程的吻合程度，载荷步数量越多，吻合程度越高。

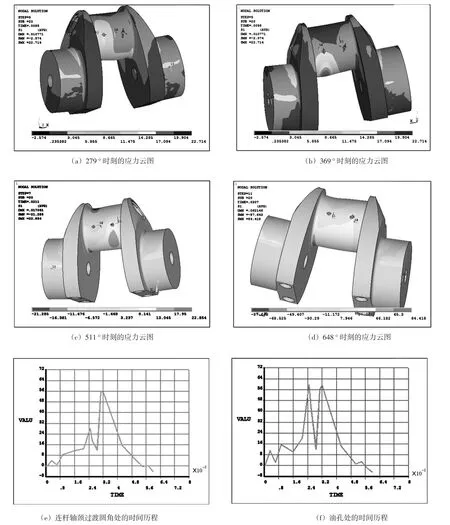
图6 不同时刻的曲轴应力云图与时间历程

对曲轴进行仿真计算前，首先在一个工作循环内选取，图4中曲线的各个拐点适当的选取平滑处的点，共计14个载荷步，如表5所示，图4为两个连杆力随曲轴转角变化，图5为14个载荷步中载荷随曲轴转角的变化，其中每一曲轴转角对应一个载荷步。

其中求解控制中设定子步数为10，最小子步数为2，最大子步数为20。

动载荷的施加是通过载荷步来完成的，对曲轴刚强度有着重大的研究意义，所以将主要对曲轴应力、位移响应结果以及重要考察部位的应力时间历程进行分析。

2 瞬态动力学结果

计算后对得到的动态应力进行分析，分别考察曲轴在100%工况下爆压时刻以及爆压时刻附近的应力变化情况。如图6所示。

综合有限元结算结果，可以得出这个工况在不同时刻的应力值，其中在爆发时刻的应力值最大，分布在主轴颈与连杆轴颈的过渡圆角处，出现的最大应力值为84.1 MPa，连杆轴颈上的油孔周围也有应力集中出现。但远低于材料的屈服极限517 MPa，具有足够的静强度。

在此工况下最大应力值处于连杆轴颈过渡圆角处，其次是出现在连杆轴颈上的油孔周围，所以通过分析结果可以得出，在连杆轴颈过渡圆角处与连杆轴颈上的油孔周围可能处于危险状态。

3 结论

针对V型发动机曲轴进行动力学分析，利用Pro/E建立三维模型，然后根据有限元理论，应用Ansys软件对曲轴单拐进行瞬态动力学分析。从结果可以看出，曲轴的应力集中在轴颈与曲柄臂连接的过渡圆角处以及连杆轴颈上的油孔处，因此在曲轴的设计过程中应该充分考虑到曲柄臂的厚度以及曲柄臂与轴颈相连的过渡圆角的大小[7]。

［1］张氢，李娟，周艳华，等.制动电阻器结构瞬态动力分析［J］.制冷空调与电子机械，2004，25（B10）：24-26.

［2］王业文.轻型港口起重机结构的动态分析［D］.上海：同济大学，2007.

［3］刘平安，熊伟，王庆立.曲轴单拐模型的有限元分析［J］.机械工程与自动化，2010（3）：8-10.

［4］李龙.五轴电火花成形机运动构件的瞬态动力学分析及结构优化［D］.苏州：苏州大学，2011.

［5］邓召文，陈涛.基于ANSYS的BN492发动机曲轴有限元分析［J］.农业装备与车辆工程，2010，229（8）：29-33.

［6］张晋伟.4125A型柴油机曲轴结构有限元动力分析［D］.杨凌：西北农林科技大学，2009.

［7］唐传茵，马岩，朱博，等.V8发动机曲轴有限元分析［J］.机械设计与制造，2013（1）：211-213.

Transient Kinetic Analysis of V-Type Engine Crankshaft Based on ANSYS

WANG Zi，SU Tie-xiong，WANG Jun
（The North University of China，Mechanical and Power Engineering，Taiyuan030051，China）

For a V-type engine crankshaft kinematics analysis，built three-dimensional model.Then based on the finite element theory，introduced the application of ANSYS software crankshaft transient dynamic analysis.Analyzed the stress and deformation cloud within a loop diagram，it can be seen from the results that the stress concentration at the crankshaft main journal fillet near the connecting rod journal fillet and a hole at the connecting rod journal on.

engine crankshaft；ANSYS；transient dynamic analysis

TP391.77

：A

：1009－9492(2014)12－0190－04

10.3969/j.issn.1009-9492.2014.12.049

王 子，男，1988年生，山西大同人，硕士研究生。研究领域：发动机结构强度与疲劳寿命分析。

(编辑：王智圣)

2014－06－09