地震时卧式容器的弯矩

李若兰，何 勇

（深圳安科高技术股份有限公司，广东深圳 518067）

地震时卧式容器的弯矩

李若兰，何 勇

（深圳安科高技术股份有限公司，广东深圳 518067）

建立地震时有附加设备卧式容器的轴向弯矩方程，解析弯矩方程，用Excel进行数据处理后画出弯矩图，确定卧式容器轴向弯矩极大值的位置和产生最大弯矩的截面，并给出工程适用的计算方法、计算式。

附加载荷；地震；弯矩方程；卧式容器

1 概述

作用在容器上的地震力是来自地面的突然的无规律的振动运动产生的，地震力造成容器损坏的主要因素是地震的强度和持续时间。地震期间，容器中的力和应力的性质是瞬态和动态的，较为复杂。为了简化设计，通常假设垂直方向具有足够的多余强度抵抗地震。从而忽略地震运动的垂直分量。作用在容器上的水平地震力则被简化为等效静态力。本章对卧式容器上有附加载荷，同时考虑地震水平力产生影响时，进行载荷分析，求出不同状态支座反力，按照载荷变化规律分段建立容器轴向弯矩方程，代入工程实例数据，利用Excel进行计算、数据处理、画出弯矩图，进而分析弯矩方程，从而得出卧式容器圆筒轴向弯矩极大值点位置、产生最大弯矩的截面。该过程得到的计算方法、计算式可以供工程设计、计算参考。

2 载荷

2.1 容器的载荷

按照Zick在实验研究基础上得出的近似分析和计算方法：置于鞍座上的卧式容器可简化成对称分布、承受均布载荷、支撑在两个铰支点上的外伸梁。卧式容器受到的外力：容器本身和物料、附件的总重量沿圆筒长度方向均匀分布的均布载荷q；梁端点作用的竖直剪力V，力偶M；以及均布载荷q作用产生的支座反力F[1]。如图1。

图1 容器受力示意图

其中：

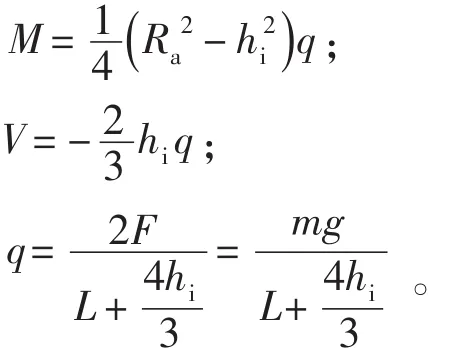
2.2 容器的附加载荷

容器上的附加载荷：把附加载荷视为集中载荷作用在受均布载荷作用的双支承外伸梁上[2]，即附属设备产生的重力mag，为方便分析假设ma处于容器中点（或中心）的左侧（通过建立适当的坐标使ma处于容器的左侧，如果假设ma处于容器中点的右侧，分析方法相同，得出计算公式不同，但是计算结果一致）。按照地震作用和结构抗震验算要求[3]，地震产生的影响力至少考虑垂直于附属设备轴线的地震力FEa的不同方向，如图1实线和虚线所示。

图1中FEa1=FEa2=FEa=α1mag。

各符号的意义同JB/T4731-2005《钢制卧式容器》。

3 支座反力

外力作用下容器鞍座处将产生以下反力。

（1）均布载荷在支座处引起的支座反力：

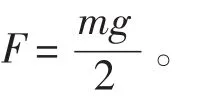
（2）附加设备重力在支座处引起的支座反力：

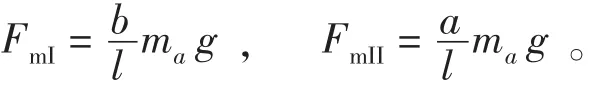
（3）地震作用引起的支座反力：

地震引起的水平力可能出现不同方向，支座反力存在下列两种情况：

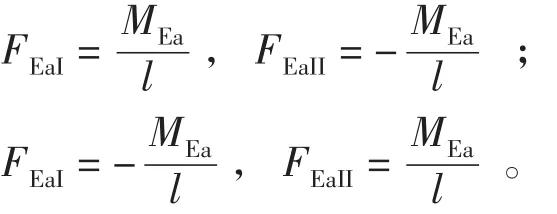
（4）支座反力组合。

同（3）说明一样，支座反力组合应当考虑两种情况：

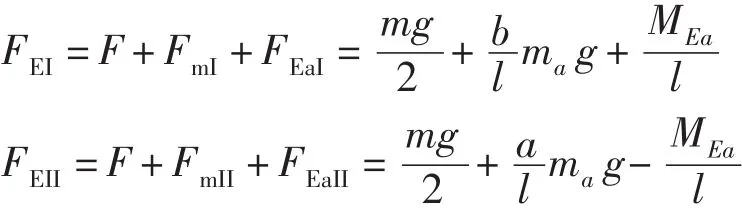
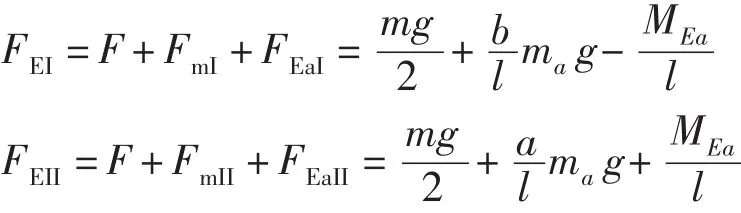
4 弯矩方程

附加载荷对支座外伸部分弯矩没有影响，因此只研究支座之间弯矩情况。

容器上的弯矩等于力偶M、竖直剪力V、均布载荷q、集中载荷mag、地震力FEa单独作用时产生弯矩的叠加。按照载荷的变化规律容器的a段、b段弯矩方程表达式不同[4]。容器简图、坐标系、符号见图2。

图2 容器简图

（1）a段弯矩方程

支座反力不同时弯矩方程的表达式将发生变化，因此a段弯矩方程有两个表达式。

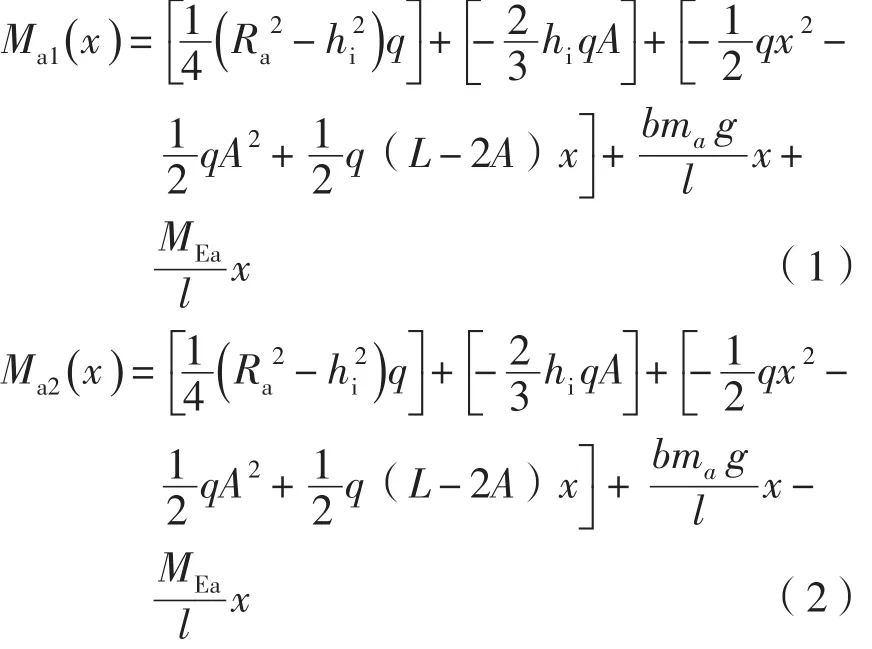
（2）b段弯矩方程

同a段一样，b段弯矩方程也有两个表达式。

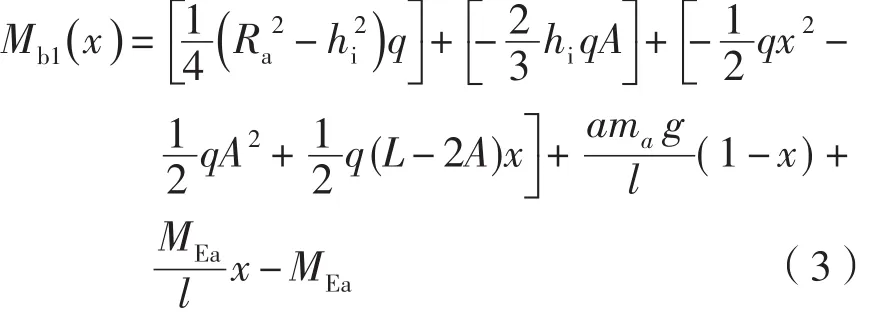
5 弯矩图

将JB/T4731-2005附录A[例3]工作状态时的数据带入以上弯矩方程，用Excel进行数据处理后做出不同载荷时的弯矩如图3。

图3中：

（1）FEa1：有附加设备重力作用，地震作用力的方向指向支座I时，容器上的组合弯矩沿轴线的变化；

（2）FEa2：有附加设备重力作用，地震作用力的方向指向支座II时，容器上的组合弯矩沿轴线的变化；

（3）有附加集中载荷：有附加设备重力作用，不考虑地震影响时组合弯矩沿轴线的变化；

（4）无附加载荷：容器上没有附加载荷作用，不考虑地震影响时容器上的弯矩沿轴线的变化。

由图3可知：

（1）地震力作用的方向不同产生的影响也不同，容器上的组合弯矩可能增加也可能减少，显然容器设计应考虑增加状态，才能降低风险；

（2）地震力作用（1、2）、集中载荷作用（3）情况下，a段上的弯矩都是单调增加的，到附加设备作用截面时达最大值；

（3）b段弯矩有极大值，极大值位于附加设备作用截面与容器中截面之间。

6 弯矩方程分析

已分析得出容器a段上弯矩单调增加，最大弯矩在集中载荷作用处。有必要对b段弯矩方程进行分析。

对b段弯矩方程取导数得：

（1）地震产生水平力的方向朝向支座I时：

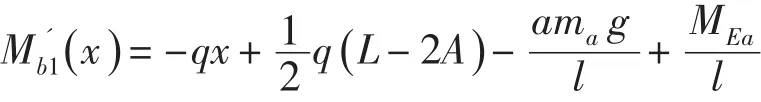
所 以 Mb1(x) 在 驻 点处有极大值。

（2）地震产生水平力的方向朝向支座II时：

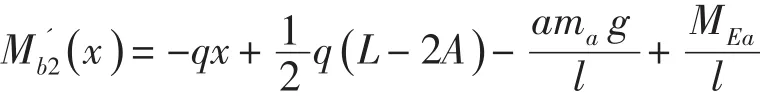
其驻点（导数等于0的点）为：

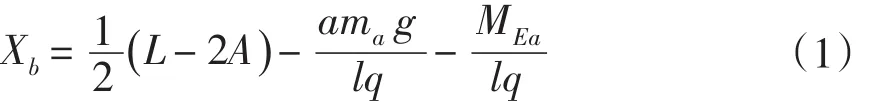
所 以 Mb2(x) 在 驻 点处有极大值。

Xb的位置和附加载荷的大小相关：附加载荷为零时，不考虑地震载荷时，，是容器的中间截面；附加载荷增加时，Xb的位置左移；随着附加载荷的增加，Xb值可能左移到a段上。

当Xb值位于b段上，说明弯矩在b段Xb处有极值，就是容器两支座之间的弯矩极大值。其值为：Mb1(Xb1)，或Mb2(Xb2)。

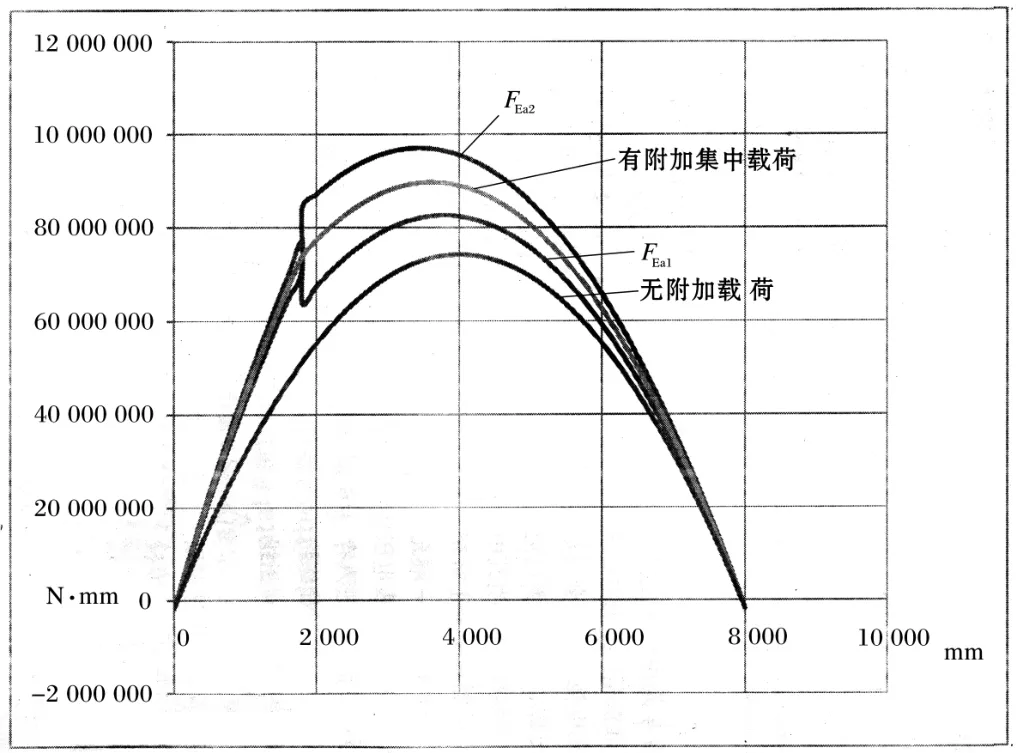
图3 容器不同载荷弯矩图

当Xb值位于a段上，说明b段上的弯矩由附加载荷作用的截面开始单调下降，此时容器两支座间的最大弯矩位于附加载荷作用的截面上。其值为：或因此，b段弯矩方程驻点位置可以作为判断容器两支座之间极大弯矩位置的准则。

7 结论

（1）地震载荷对容器弯矩的叠加作用，在集中载荷作用截面上弯矩发生突变，使该截面上的弯矩在无地震力作用时的基础上增加或减少。减少情况下容器轴向弯矩少于无地震力作用状态。显然卧式压力容器设计考虑地震载荷时，应考虑其产生的增加作用。

（2）取图2所示坐标系，地震力方向朝支座II产生的弯矩将在集中载荷作用的基础上增加。

（3）弯矩极大值的确定

计算容器b段弯矩方程的驻点，就能确定容器两鞍座之间的轴向弯矩极值产生的位置。以及轴向弯矩的计算方法。步骤如下：

计算b段弯矩方程的驻点：

判断驻点Xb2的位置，即Xb2值所在区间。Xb2值在b上，表示b段弯矩有极大值，Xb2为极大值所在位置。弯矩极大值为：Mb2(Xb2)。

（4）容器上最大弯矩

Xb值在b段上，b点的弯矩是容器的最大弯矩。Mmax=Mb2(Xb2)。

Xb值在a段上，A-A截面上的弯矩是容器上的最大弯矩。Mmax=Mb2(a)。

［1］JB/T4731-2005.钢制卧式容器［S］.

［2］李世玉.压力容器设计工程师培训教程［M］.北京：新华出版社，2005.

［3］GB50011-2010.建筑抗震设计规范［S］.

［4］李若兰，丁杰，聂莉莹.卧式容器外加两个集中载荷时的轴向应力计算［J］.压力容器，2008，25（10）27-29.

The Bending Moment of Horizontal Pressure Vessels on Saddle Supports During the Earthquake

LI Ruo-lan，HE Yong
（Shenzhen Anke High-tech Co.，Ltd.，Shenzhen518067，China）

The bending moment equation of horizontal pressure vessels with additional equipment during the earthquake was established. Drawing bending moment diagram after the data was processed by excel and analyzing bending moment equation to determine the max axial bending moment position and the greatest bending moment cross-section for the applicable calculation method and calculation formula in engineering was given.

additional load；earthquake；bending moment；horizontal vessel

TH123

：A

：1009－9492(2014)10－0072－04

10.3969/j.issn.1009-9492.2014.10.020

李若兰，女，1957年生，福建莆田人，大学本科，高级工程师。研究领域：磁共振成像设备，压力容器，制冷设备技术。已发表论文6篇。

(编辑：向 飞)

2014－04－22