实心式永磁电机轴承载荷分析

武文虎，李有生，王志林，李树龙

（山西北方机械制造有限责任公司，山西太原 030009）

实心式永磁电机轴承载荷分析

武文虎，李有生，王志林，李树龙

（山西北方机械制造有限责任公司，山西太原 030009）

研究实心式永磁电机轴承载荷的影响因素，提出载荷计算方法。以TYCKK3554-4（6kV 250 kW）电机为例进行分析计算。影响轴承载荷的主要因素有：单边磁拉力、转子偏心量旋转惯性离心力、转子自重及负载不平衡力的影响。研究为电机轴承选取提供依据，对提高电机可靠性和运行寿命有很大意义。

永磁电机；轴承；分析

0 引言

实心式永磁电机在交变磁场、冲击载荷条件下工作，要求所选用的轴承具有较高的刚度。实心式永磁电机由于采取涡流启动，在电机启动及运行过程中对轴承的作用将不同于异步电机。为证明实心式永磁电机的工作正常、可靠，以TYCKK3554-4（6kV 250 kW）电机为例，选用轴承为6224，分析轴承载荷影响因素并对轴承进行合理的分析与计算，使其性能指标满足使用要求。

1 影响因素分析

（1）永磁电机工作在交变磁场中，而轴具有自身的挠度，由此产生的单边磁拉力对轴承具有交变冲击载荷[1]。

（2）转子在加工制造及安装过程中将产生误差，转子将产生偏心，由于偏心带来的离心力对轴承也将产生冲击载荷。

电机负载的不对称性对轴承也有一定的冲击载荷。

2 轴承载荷计算

2.1 单边磁拉力影响

若电机转子在定子内偏心，则造成空间气隙不对称，产生定子对转子的单边磁拉力，其中定子与转子的偏心主要由轴的挠度及单边磁拉力共同影响。

2.1.1 轴承自重引起的挠度

轴伸处无作用力时，两轴承由转子自重引起挠度，其中轴的当量直径为[2]：

其中：li为阶梯轴i段的长度；

di为阶梯轴i段的直径；

L为两支乘之间的长度。

解析获得dm=123.612 6 mm。

通过挠度计算公式获取轴的最大挠度为：

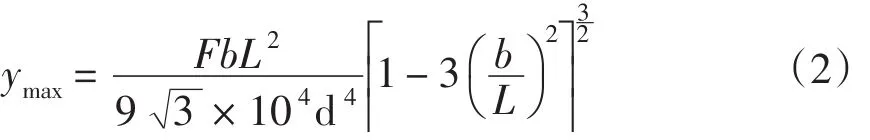
其中：F为阶梯轴自重；

d为阶梯轴的当量直径；

b为轴伸端支撑到转子质心距离；

L为两支撑之间的长度。

计算得ymax=0.114 2 mm。

2.1.2 单边磁拉力引起的轴的挠度

单边磁拉力一般认为集中在重力所作用的同一截面处，在单边磁拉力的作用下，使转子相对于定子在初始偏心的基础上，再增加一个附加的偏心，后者又进一步引起附加的单边磁拉力，这样一直进行下去。但这些附加的单边磁拉力和相应的附加挠度都是逐渐减小的，因此最后将达到稳定状态，此时，它与轴的弹性力向平衡，保证轴的平稳运行。

根据单边磁拉力挠度计算公式：

式（3）中，K0为磁拉力刚度；

K为轴的弯曲刚度；

fG为转子的初始偏心，大小为0.114 2 mm。

可知，由单边磁拉力引起的挠度与轴的弯曲刚度、磁拉力刚度及定子与转子的初始偏心有关。

根据公式：

计算得轴的弯曲刚度为45.653 kN/mm。

式（4）中G为转子总重；

fG为轴伸处无作用力时，两轴承有转子自重引起的挠度，大小为0.114 2 mm。

根据公式：

计算得磁拉力刚度为7.603 2 kN/mm。

式（5）中 β为经验系数，取值0.4；

D为定子内径，取值360 mm；

lef为铁芯有效长，取值365.07 mm；

Bδ为气隙磁密；

δ为单边平均气隙，取值6.75 mm。

为求解Bδ的大小，对电机进行模型仿真，得出气隙磁密曲线如图1所示。

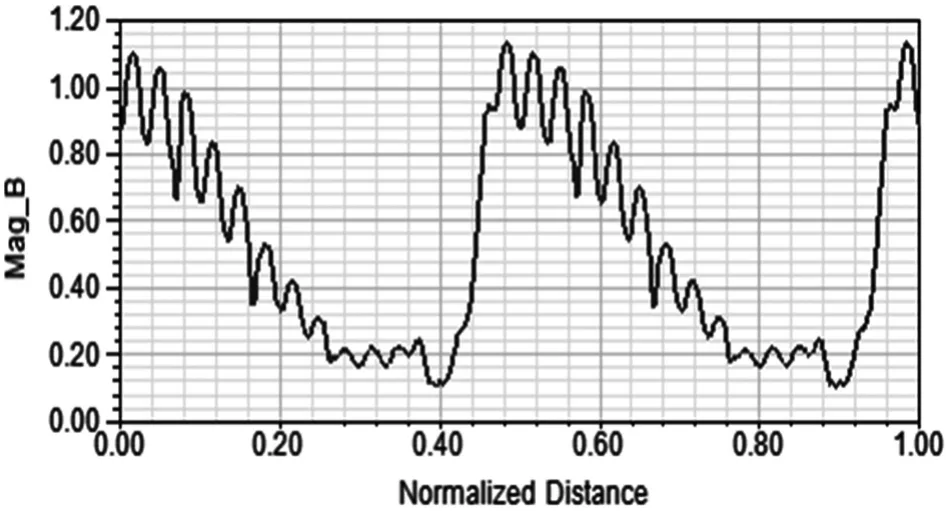
图1 气隙磁密分布图

根据图1分析得出最大气隙磁密均值为0.9 T。

因此，由公式（3）计算得出单边磁拉力引起的轴的挠度为0.03 mm。

2.1.3 轴的总挠度

由上可知，在轴承中部处产生的总挠度为0.144 2 mm。为保证电机能安全可靠运行，电机总挠度应不超过电机气隙值的8%，计算得出总挠度满足要求。

通过此时的总挠度计算得出单边磁拉力为1.1 kN。

2.2 转子偏离转动中心的影响

影响转子偏离转动中心的因素主要有以下几点。

（1）制造质量问题。转动件不均匀、几何不对称，质心偏离几何中心。

（2）安装质量问题。轴及叶轮安装摆度使几何中心偏离转动中心。

（3）运行时，电机轴线、转子温度场不对称，引起变形、弯曲，造成弓形旋转，质心偏心距变化。

轴线偏心主要是由于转子在自重及单边磁拉力的作用下产生的挠度，同时由于转子质心偏离转动中心，二者共同作用产生离心力。

由公式：

得知离心力为1.469 kN。

式（6）中m为转子重量；

ω为转速；

r为转动偏心距。

2.3 过盈装配产生的应力

采用Ansys接触分析[3]获取其过盈转配时的接触应力，设置轴的轴径为110 mm，同时设置过盈量为0.035 mm，分析结果见图2所示。

分析得到此时加载到轴承上的载荷为43.12 kN。

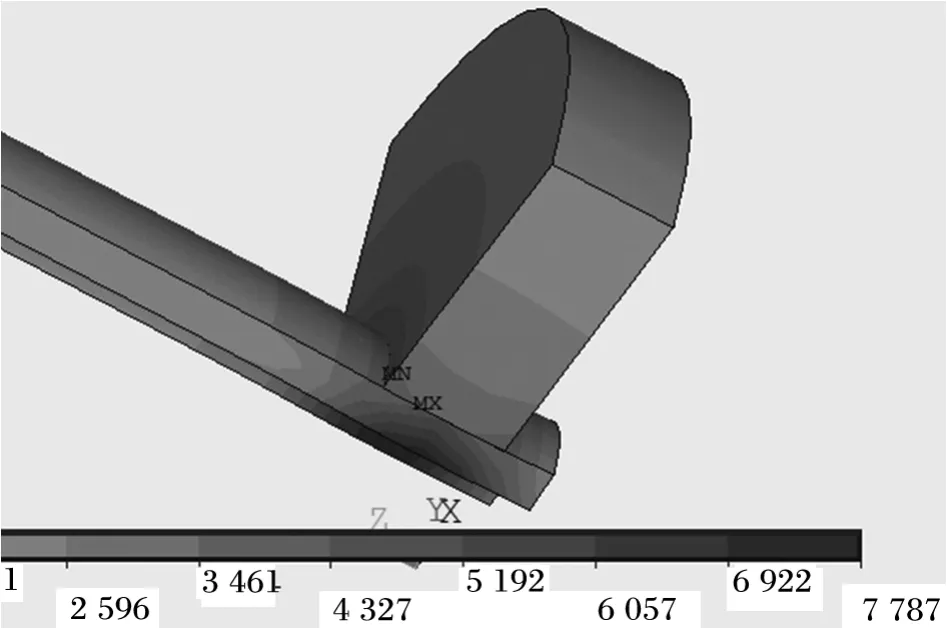
图2 接触应力图

2.4 转子自重影响

本电机转子质量为521.36 kg，其自重为5.109 kN。

2.5 外部载荷影响[4]

考虑外部载荷对电机影响因素约为1.5倍转子自重，即7.66 kN。

2.6 静态分析计算

以破坏试验为方法，通过上述分析得出后轴承承载力约为54.53 kN。

考虑力矩载荷的当量动载荷，采用力矩载荷系数2，轴承冲击载荷系数1.2，得到后轴承的当量动载荷为130.87 kN。

通过机械设计手册[5]得出该轴承的基本额定动载荷为312 kN。计算得出结果小于额定动载荷，轴承可以正常使用。

3 动态载荷分析计算

为验证分析计算结果，建立转轴与轴承的三维模型，迫使轴承承受周期载荷作用，获取轴承在不同时间内承受载荷情况见图3所示。

由图3分析得知，在循环载荷下，轴承承受载荷力为48.3 kN，与第二部分静态分析结果基本一致，此分析方法结果可靠。

图3 动载荷应力图

4 结论

通过上述分析获得永磁电机轴承寿命影响因素主要为单边磁拉力、转子偏心量旋转惯性离心力、转子自重及负载不平衡力，通过这些影响因子的计算可以获取永磁电机轴承寿命，为永磁电机合理选用轴承提供理论依据。

［1］武文虎，李有生，王志林.电机壳体侧壁优化设计［J］.机电工程技术，2014（09）：35-37.

［2］陈世坤.电机设计［M］.北京：机械工业出版社，2011.

［3］苏荣华，梁斌.结构仿真分析-ANSYS应用［M］.沈阳：东北大学出版社，2005.

［4］仇宝云.大型立式轴流泵导轴承载荷分析计算［J］.煤矿机电，2006（5）：92-93.

［5］闻邦椿.机械设计手册［M］.北京：机械工业出版社，2011.

Study of Bearing Load in Solid Type Permanent-Magnet Machine

WU Wen-hu，LI You-sheng，WANG Zhi-lin，LI Shu-long
（Shanxi North Machine-Building Co.，Ltd.，Taiyuan 030009，China）

This paper studies of bearing load’s effect factors in solid type permanent-magnet machine，proposes the load calculation method，analyzes and calculates by the example of the TYCKK3554-4(6kV 250 kW).The main factors affecting the bearing load are unilateral magnetic force，eccentricity of the rotor rotating inertial centrifugal force，gravity and load unbalance force.This study provides the basis for the selection of motor bearing，and has great significance to improve the reliability and service life of motor.

permanent-magnet machine；bearing；analysis

TM351

：A

：1009－9492(2014)10－0091－03

10.3969/j.issn.1009-9492.2014.10.025

武文虎，男，1986年生，山西吕梁人，硕士，工程师。研究领域：高效高压永磁同步电机。已发表论文3篇。

(编辑：王智圣)

2014－04－10