三元DNA Golay码的构造*

2014-02-10白姗姗

通信技术 2014年10期

关键词：码字碱基探针

冯宾,白姗姗

(安徽理工大学理学院,安徽淮南232007)

三元DNA Golay码的构造*

冯宾1,白姗姗2

(安徽理工大学理学院,安徽淮南232007)

Golay码是一类比较好的线性码,并且是仅有的两类达到Hamming界的完全码中的一类。而DNA编码是近几年纠错码界研究的热点,且比传统纠错码具有更新更好的一些性质。它是DNA计算中的重点和难点问题,且是核心问题,所以合理的DNA编码可以提高实验的稳定性和正确性,从而确保DNA计算的成功率。所以,用传统纠错码构造DNA纠错码是一项有意义的工作。本文给出了利用三元Golay码G12和G11构造三元DNA Golay码D12和D11的方法,并给出了这两种三元DNA Golay码的性质。

线性码 Golay码 DNA Golay码

0 引言

近年来[1],不少学者发展了很多MP(Matching Pursuits)算法的改进算法,均具有一定的实际意义。其中,遗传算法(GA,Genetic Algorithm)模拟了达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。类似遗传算法的理念,DNA计算是生物学、数学和计算机的交叉性研究领域。由于DNA计算是以组成生命的遗传物质DNA分子进行编码并处理信息的,因此编码问题随着DNA计算的研究引起研究人员的注意。对DNA编码的研究在最近几年已有了很大的进展:20世纪90年代,DNA码字间相似度的编码方法,DNA编码的定义以及对DNA杂交错误的防错编码策略的分析分别由Baum和Garzon提出;21世纪初,DNA码字间相似度的计算方法和形式评价准则,模板编码方法,单模板编码方法,三字母表的编码策略,随机搜索优码方法分别由Feldkamp,Frutos,Arita,Braich,Tulpan提出,并得到了质量较好的DNA码;Feldkamp等人给出了另一种定义序列间相似度的方法,用来衡量两个编码间的相似度,并给出了一个基于前缀树的编码构造算法,即最大相同子串。在此基础上,又开发出了根据各种要求生成编码的软件包。Braich等人提出了可以降低DNA分子生产二级结构的三字母表编码策略。在这方面,数学家也做了一些研究工作并发现:最大相同子串的约束性非常强,其编码数量随编码长度的增加变化不大。Suyama等人提出了正交编码数的概念,此外,Adleman和Winfree的研究小组也有针对具体问题而进行的编码方法研究。应该说,编码问题的研究,不仅对DNA计算,而且在生物芯片的设计及其它方面也有广阔的应用。

另外,王淑栋[2]等人在2009年提出:利用二元Golay码G24=[24,12,8]和G23=[23,12,7]构造二元DNA Golay码D24和D23的设计思路,并定义了DNA码字重量和Watson Crick Hamming距离。本文借助此结论的原理,对二元DNA Golay码的构造进行了推广:利用三元Golay码G12=[12,6,6]和G11=[11,6,5]构造三元DNA Golay码D12和D11,并给出了它们的几个特殊性质。

1 基本概念

1.1 DNA计算中的编码问题

杂交反应[3]是DNA计算中最核心的反应,并且它的可靠性依赖于DNA分子间的特异性杂交。从而,DNA计算的效率和最终输出结果的可靠性依赖于杂交反应的效率和精度。研究表明,DNA分子间的杂交反应在完全互补配对和不完全互补配对的情况下都有可能出现错误。研究人员把这两种错误杂交分别称为假阴性和假阳性,由于种种因素的影响,完全互补的DNA分子没有杂交成功,此种错误被称为假阴性;在合适的条件下,不完全互补的DNA分子也有可能杂交形成双链分子,此种错误称为假阳性。导致假阴性发生的主要原因是反应条件以及生化操作的失误;而导致假阳性发生的主要原因是杂交的两个DNA分子在很大程度上是互补的。编码研究的主要目的就是为了能够最大限度地对实际生化反应过程中的DNA序列进行唯一且准确的识别,使得计算过程能够尽量按照模型的方向进行。从而,为了达到DNA计算能够顺利且可靠地进行下去的目的,我们必须想办法,尽可能地降低错误杂交发生的概率。

下面给出DNA计算中编码问题的定义:

在字母集合{A,G,C,T}上,长度为n的DNA分子一共有4n个,它们组成的集合记为S。取k为正整数,令ζ是评价编码性质的准则(Hamming距离、最小相同子序列数目、移位距离等),则所有满足公式ζ(si,sj)≥k(其中si和sj是S中的两个编码)的DNA分子构成集合C,C是S的子集。

取矩阵G=(gij)m×n(gij=0,1,2,3),A= (a1,a2,…,am)∈{0,1,2,3}m,对A的编码过程W= A×G,其中A为信息元,W称为码元,G为线性码的生成矩阵。对于信息元A可以取4m个行向量,因此生成4m组码元,即4m个长度为n的线性码。当G为生成矩阵的标准形式时,生成的线性码为系统码,系统码是线性码中最重要的一类码。

1.2 DNA计算编码的约束条件

有很多因素(化学自由能变化、生物酶、解链温度、DNA分子的生物特异性等)都会影响DNA的计算,序列编码的约束条件就是由这些因素所决定的。在前人研究成果的基础上,对影响DNA计算的这些因素进行综合考虑,给出了DNA计算的线性编码约束条件。

用来编码信息元的序列称为字序列(word sequences),表示为xi;与之互补的序列称为探针序列(probe sequences),表示为x′i。DNA分子中碱基A与碱基T互补配对,碱基G和碱基C互补配对。连接字序列与字序列所组成的序列叫做库序列(Library sequences),表示为Ln=〈xi,xj,…,xk〉,由库序列构成的集合{Ln}与待计算问题的全体基本解空间相对应。

约束DNA计算编码的条件:DNA计算的编码是在字母表∑={A,T,C}上进行的。

在三字母表{A,T,C}上进行编码,编码序列中就没有了碱基G,从而探针序列中就没有了碱基C。这样以来,库序列与库序列之间、探针序列与探针序列之间就不会完全匹配;探针序列要正确匹配,只能选择和库序列进行匹配;并且各编码序列自身与自身之间很难形成“发夹结构1”,同时编码序列与其他编码序列之间形成“发夹结构2”的可能性也大大地减小了。采用这种编码方法也使编码序列的生物特异性得到明显提高,但它也是有缺点的,由于可用字母由4个变到3个,使得可用编码的数量急剧减少,可用编码的数量从4l个下降到了3l个(l表示字序列的长度),字序列长度为15时,整整下降了两个数量级。然而针对现在DNA计算的规模,利用三字母表编码仍然是非常有效的。

1.3 线性编码方法

目前,DNA计算中的重点和难点仍然是编码问题。实践已证明:利用有效的编码设计,能够提高DNA计算过程中的可靠性。最小Hamming距离是DNA计算编码的重要参数,它决定了编码序列DNA分子的生物特异性,与DNA分子在杂交反应中自由能变化直接相关,是计算可靠性的重要因素。用线性码构造满足Hamming距离的DNA编码是一种非常有效的方法,关键在于构造相应的监督矩阵。

在DNA编码中,用数字“0,1,2,3”来表示字母“A,T,C,G”时,就可以用四进制数序列表示DNA编码序列,这时DNA编码的最小Hamming距离就可用线性系统码来构造。在线性码运算中,所有的运算均是指模运算,用剩余类的代表元表示运算结果。对于四进制的线性码,我们采用模4运算。当DNA序列用三字母表{A,T,C}进行编码时,我们用数字“0,1,2”表示“A,T,C”,这时DNA编码序列就变成三进制数序列,对于三进制的线性码采用模3运算。

2 三元DNA Golay码的构造方法

2.1 三元Golay码的定义

线性码[4]是纠错码当中的一部分(因为线性码不仅是Fq的子集合,而且要求是Fq的线性子空间),并且多数性能良好的纠错码都是线性码。Golay码就是一类较好的线性码,即完全线性码(参数为[n,k,d]的q元码叫作完全码,是指它达到Hamming界)。

1949年,Golay发现了两个完全线性码。一个参数为[n,k,2l+1]的q元完全码要满足,但是满足这个等式的n,k,d(=2l+1)和q(为素数幂)是很少的。Golay首先求出满足这个等式的三组参数为(q,n,k,d)=(2,23,12,7), (2,90,78,5)和(3,11,6,5),并且他证明了参数为[90,78,5]的二元线性码是不存在的。然后通过精细的组合学考虑,构作出了二元线性码[23,12,7]和三元线性码[11,6,5]。下面给出两种三元Golay码的生成方法:

(1)以矩阵

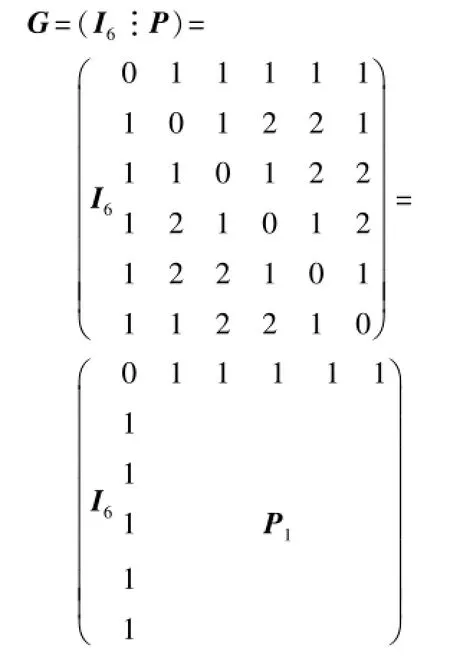
为生成阵的三元线性码G12是参数为[n,k,d]= [12,6,6]的自对偶码。(其中F2上6阶方阵P的构作方式是:左上角的元素为0,第1行和第1列中的其他元素均为1,剩下的5阶方阵P1的第1行为(01221),而其余诸行依次为第1行向右循环移位。)

(2)将G12中所有码字去掉末位,得到的收缩码G11是[n,k,d]=[11,6,5]的三元线性码,并且是完全码。

2.2 三元DNA Golay码的构造

碱基“A,T,C”用数字“0,1,2”来表示,这样三进制数序列就可以用来表示编码序列。类似二元DNA Golay码的构造方法,给出三元DNA Golay码的构造过程:

构造映射f:G12→D12如下:在G12中任取三进制码字x=x1x2…x12,如果xi=j,则记f(xi)∈∑j(j=0, 1,2;i=1,2,…,12)。这时x对应的三元DNA Golay码字就是f(x),称三元Golay码G12在映射f下得到DNA Golay码D12。用同样方法能够构造出三元DNA Golay码D11。

对于G12(G11)中的一个三进制码字x,它唯一的与DNA Golay码f(x)相对应;并且对于一个DNA Golay码字f(x)∈D12(D11),其对应的三元Golay码字也是唯一的,因此f是一个一一映射。即每一个三元DNA Golay码字都唯一的与一个三元Golay码字相对应,更好地满足了DNA计算编码中对生物特异性的要求。并且利用三字母表{A,T,C}进行编码时,在编码序列中不含有碱基G,探针序列中不含有碱基C,这样库序列和库序列、探针序列和探针序列之间就不可以进行完全的匹配,探针序列只可以和库序列进行正确的匹配,比较重要的一点是:各编码序列自身与自身之间很难形成“发夹结构”。从而,三元DNA Golay码优于二元DNA Golay码。

例:取信息元A中的一些码字a1=(020112), a2=(201210),a3=(111021),a4=(010212),则它们对应的Golay码分别为:

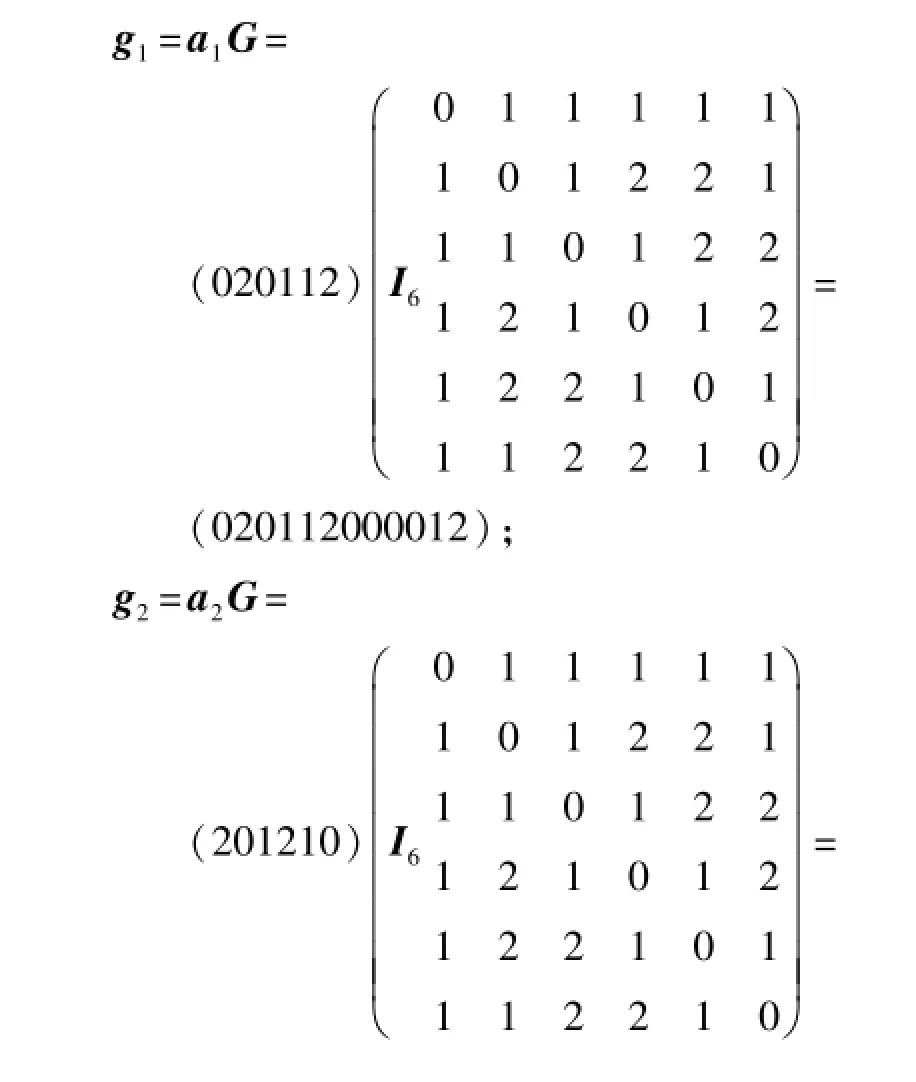
从而g1,g2,g3,g4∈G12且为系统码,分别唯一的对应DNA Golay码字:

去掉码字的最末位,得到:

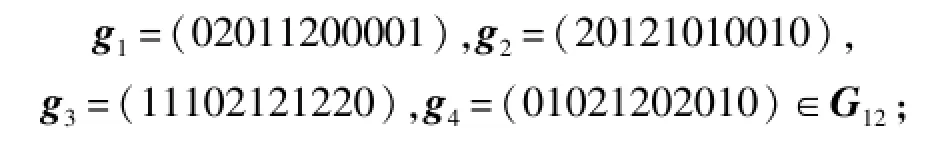
它们对应的DNA Golay码字分别为:

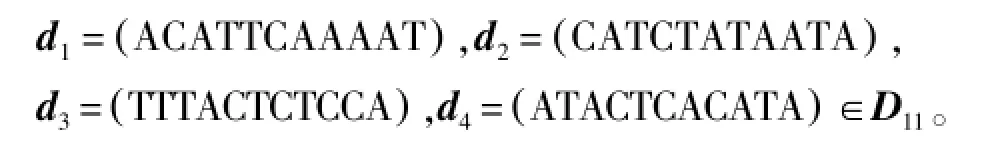
其对应表格如下:

信息元Golay码DNA Golay码收缩Golay码收缩DNA Golay码(020112)(020112000012)(ACATTCAAAATC)(02011200001)(ACATTCAAAAT) (201210)(201210100100)(CATCTATAATAA)(20121010010)(CATCTATAATA) (111021)(111021212200)(TTTACTCTCCAA)(11102121220)(TTTACTCTCCA) (010212)(010212020100)(ATACTCACATAA)(01021202010)(ATACTCACATA)

显然,三元DNA Golay码与三元Golay码是一一对应的。

2.3 三元DNA Golay码的性质

为了进一步讨论DNA Golay码的性质,我们定义DNA Golay码字间的加法、减法和乘法运算如下:

定义在f的逆映射f-1下,对D12(D11)中的任意码字x,y与G12(G11)中的码字x′,y′唯一对应。定义x+y=f(x′+y′),x-y=f(x′-y′),x*y=f(x′×y′),其中x′+y′,x′-y′和x′×y′分别是三元域上的加法、减法和乘法运算。

三元DNA Golay码的性质与二元DNA Golay码的性质相类似,表示如下:

引理2.1 三元Golay码G12和G11都是线性码,且参数分别为[12,6,6]和[11,6,5]。

性质1 DNA Golay码D12和D11是线性码。

证明：在映射f-1下,任意的x,y∈D12,存在唯一的x′,y′∈G12与之对应。由引理2.1知,G12是线性码,则有x′+y′∈G12,αx′∈G12(α∈{1,2,3})成立。从而x+y=f(x′+y′)∈D12,αx=f(αx′)∈D12,由线性码的定义知D12是线性码。同理可证D11也是线性码。证毕。

引理2.2Golay码G11是完备码。

性质2DNA Golay码D11是完备码。

证明：由引理2.2知,Golay码G11是完备码。因为Golay码G11中的码字在映射f下一一对应于DNA Golay码D11中的码字,因此两者是等价的,并且DNA Golay码D11的规模等于Golay码G11的规模,从而DNA Golay码D11也是完备码。

3 结语

本文在前人研究的基础上,首次利用三元Golay码构造出了三元DNA Golay码,这种码比传统纠错码多了新性质,并且在DNA计算中具有很好的潜在实用性;同时,对DNA计算编码的构造方法也做了新的尝试和有益的补充。但是,如何将这些DNA Golay码应用到实际的DNA计算当中,还是有待解决的。所以,我们需要继续对这些问题做深入的研究和探讨。

近几年来,在编码理论学者的共同努力下,DNA计算编码的构造有了很大的突破,一些新的DNA编码相继被构造出来。对于编码理论学者来说,利用更加简便快捷的方法构造出更多性能良好的DNA编码是未来研究的重点。

[1] 高丽贞.结合遗传算法的匹配追踪算法的性能分析[J].通信技术,2013(08):153-155.

GAO Lizhen.Matching Pursuit Algorithm of Genetic Algorithm Combining with Analysis of the Performance[J]. Communications Technology,2013(08):153-155.

[2] 王淑栋,宋涛,李二艳.DNA Golay码的设计与分析[J].电子学报,2009(07):1542-1545.

WANG Shudong,SONG Tao,LI Eryan.The Design and Analysis of DNA Golay Codes[A].Beijing:Acta Electronic Sinica,2009(07):1542-1545.

[3] 朱翔欧,刘文斌.DNA计算中的编码问题[M].北京:清华大学出版社.2012:21-24.

ZHU Xiangou,LIU Wenbin.Coding Problems in DNA Computing[M].Tsing hua university press.2012:21-24.

[4] 冯克勤.纠错码的代数理论[M].陈朝晖.第一版.北京:清华大学出版社.2005:22-29.

FENG Keqin.Algebraic Theory of Error-Correcting Codes [M].CHEN Zhaohui.The first edition.Beijing:Tsing hua university press.2005:22-29.

FENG Bin(1986-),female,graduate student,mainly working at theory and application of error-correcting codes.

白姗姗(1989—),女,硕士研究生,主要研究方向为纠错码理论及应用。

BAI Shan-shan(1989-),female,graduate student,mainly working at theory and application of error-correcting codes.

Construction of Ternary DNA Golay Codes

FENG Bin1,BAI Shan-shan2
(College of Science,Anhui University of Science&Technology,Huainan Anhui 232007,China)

Golay code is a fairly good linear code and one of the only two perfect codes reaching the Hamming periphery.In recent years,DNA encoding,as a research hotspot of error-correction code,enjoys some updated and better properties than traditional encoding,and is also the key problem in DNA computing,thus reasonable DNA coding could improve the reliability and stability of experiment and ensure the successful rate of DNA computation.Obviously,the construction of DNA codes by using traditional codes is of significant importance.How to construct ternary DNA Golay codes D12and D11by using ternary Golay codes G12and G11is described and the properties of these two ternary DNA Golay codes are also given in this paper.

linear codes;Golay code;DNA Golay code

10.3969/j.issn.1002-0802.2014.10.004

TP18

1002-0802(2014)10-1125-05