波达信号功率谱分布对信号接收衰落相关性的影响*

周 杰,刘 鹏,菊池久和

(1.南京信息工程大学电子与信息工程学院,江苏南京210044; 2.日本国立新泻大学工学部电气电子工学科,日本新泻950-2181)

波达信号功率谱分布对信号接收衰落相关性的影响*

周 杰1,2,刘 鹏1,菊池久和2

(1.南京信息工程大学电子与信息工程学院,江苏南京210044; 2.日本国立新泻大学工学部电气电子工学科,日本新泻950-2181)

本文推导波达信号功率谱对MIMO(Multiple Input Multiple Output)多天线信号接收衰落相关性通用式,并分析了在各种功率谱分布下的接收信号相关性。结果证明分析可以很好地应用于波达信号功率谱为高斯分布、拉普拉斯分布和均匀角分布时的信道情况。在功率谱分布是双边分布时,导出了其接收信号衰落相关性特征。分析结果发现功率谱分布的标准偏差或角度扩展大小是确定接收信号衰落相关性的主导因素。数值结果表明在一定范围内增大天线阵列单元间的距离以及功率谱分布标准差可以减小天线阵列接收信号衰落相关性,改善系统性能。在阵列天线单元间在中长距离内,功率谱高斯分布更符合实际和有利于分析和提高无线信道多天线MIMO系统性能。

波达信号功率谱 信号衰落相关性 电磁传播 双边分布

0 引 言

近年多天线MIMO(Multiple Input and Multiple Output)技术及其应用已成为当今移动通信技术中最重要的研究领域之一,下一代无线通信系统是一个基于在全球不同网络间传输的混合的移动服务的重要通信系统,无线系统的性能主要取决于无线信道特性,因此,研究无线通信系统首先要研究无线通信信道传播模型。在复杂的无线通信环境下,电波传播多径现象是造成的信号衰落的重要问题,多径效应在信道中的小尺度衰落是无线信道研究的重点内容之一,多径衰落严重损害了移动通信系统的性能。为了克服多径效应这个问题通常利用信号处理方法进行天线阵列的分集接收技术,该技术被认为是提高信道容量和克服多径衰落的最有效无线传输技术。然而MIMO天线阵列的性能主要依赖于天线之间的空间接收信号衰落相关性,文献[1-2]分析结果为分集接收时分集增益也会随着天线阵元间衰落信号相关性下降。文献[3-5]依靠数值积分和无限级数来计算波达信号功率谱分布下的MIMO天线阵列单元间的接收信号衰落相关性。

本文推导波达信号功率谱对MIMO信号接收衰落相关性通用式,并分析了在各种功率谱分布下的接收信号相关性[6-12]。结果证明分析可以很好地应用于波达信号功率谱为高斯分布、拉普拉斯分布和均匀角分布时的信道情况。在功率谱分布是双边分布时,导出了其接收信号衰落相关性特征。分析结果发现功率谱分布的标准偏差或角度扩展大小是确定接收信号衰落相关性的主导因素。数值结果表明在一定范围内增大天线阵列单元间的距离以及功率谱分布标准差可以减小天线阵列接收信号衰落相关性,改善系统性能。在阵列天线单元间在中长距离内,功率谱高斯分布更符合实际,有利于分析和提高无线信道多天线MIMO系统性能[8-9]。结果显示近似算法可用以准确地分析和仿真系统误码率性能,且算法式同样可以被用于分析多边波达信号以及多种功率谱分布下的MIMO多天线阵列接收信号衰落相关性参数。

1 MIMO接收信号衰落相关性理论

影响无线通信系统中信息可靠传输的主要因素,一是多径效应所引起的时延扩展,二是信道时变性所引起的频谱扩展,三是空间相关性所引起的角度扩展。所有的因素的限制都导致在无线衰落环境中需要付出更多的代价。本文主要研究MIMO多天线结构与空间因素引起的接收信号衰落相关性。假设MIMO多天线阵列为线性阵列,波达信号为平面波信号当到达天线阵列时的角度为θ,且两个天线阵元之间距离设为d时,可知在天线阵元的接收信号可分别表示为s1=m(t)和s2=m(t)e-j2πd/λsin(θ),如果假设天线阵元均为全向方向图,即m(t)=1,可得E{s1(i)(i)}=ej2πd/λsin(θ)。因此对MIMO多天线阵元数为M的阵列,其各天线单元的接收信号响应向量ν(θ)可表示为[13-15]:

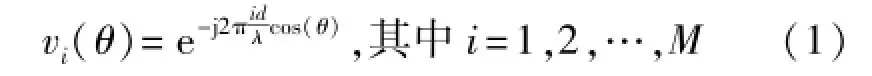
式中d和M分别表示天线间距和阵列天线数目。因此MIMO天线阵列的阵元m和n的空间相关性可以表示为[6-11]:

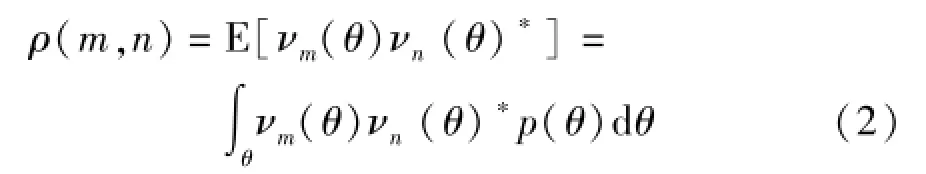
式中p(θ)为波达信号功率谱。由式(1)代入式(2),稍加变换即可将阵元间距离为d时的两阵元接收信号衰落相关性为:

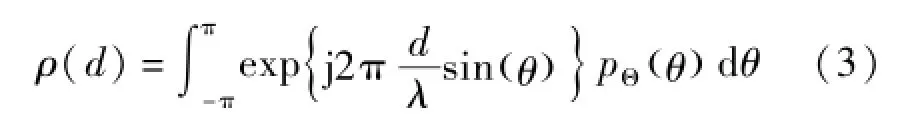
假设波达信号功率谱分布为高斯角能量分布函数。其角能量分布函数可为[15]:

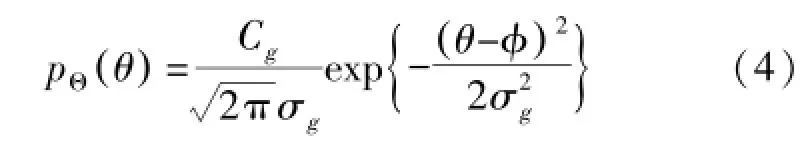
式中σ是功率谱分布的标准差,Cg是分布密度函数归一化常数[15]。φ是波达信号中心到达角AOA (Angle of Arrival)。

假设波达信号服从高斯分布的功率谱,其分布函数可表示为:

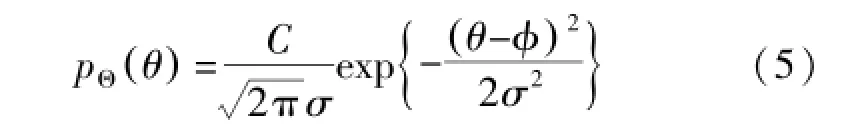
式中σ是分布的标准差,φ是中心到达角。MIMO任意两阵列单元间信号空间相关性可表示为:

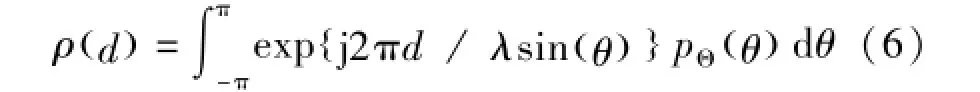
将式(5)代入到(6)中,经推导和变量变换可得到:

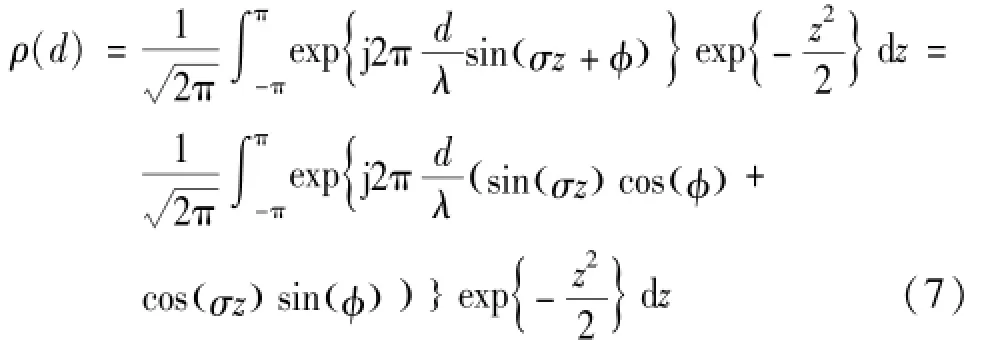
假设当exp{-z2/2 }dz是有意义的,而且σz是在较小取值范围,那么近似式可得:

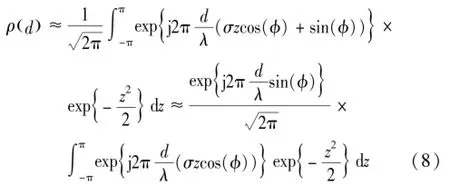
计算式(8)积分,可得到MIMO多天线阵列任意两单元间接收信号衰落相关性近似计算方程为:

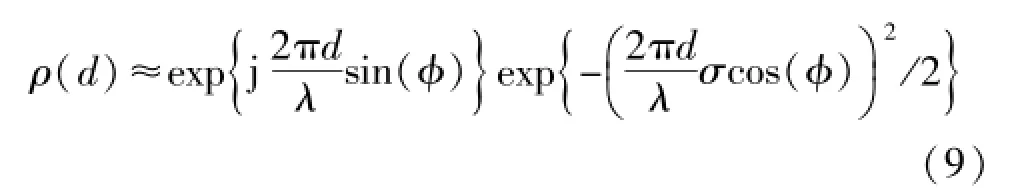
从公式(9)中可看出能够利用2πdσcos()/λ为参数对其接收信号衰落相关性进行计算和分析。另一种常用波达信号功率分布为均匀角能量分布函数[4]。其函数表达式为:

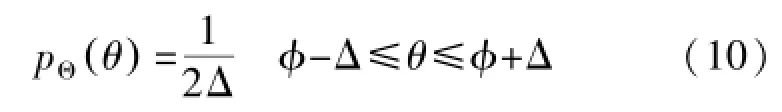
式中2Δ是波达信号AOA到达角的范围。

将式(10)代入到(6)中,经推导和变量变换可得到:

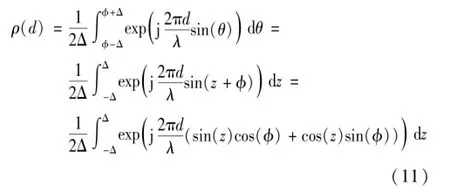
对较小Δ值时可近似认为sin(z)≈z和cos (z)≈1,可以得到:

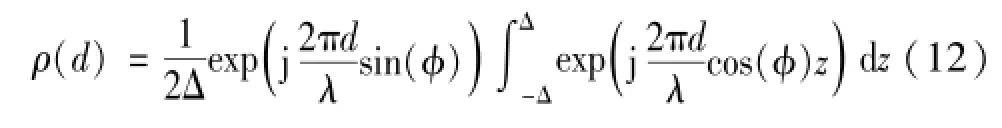
计算式(12)积分,可得到MIMO多天线阵列任意两单元间接收信号衰落相关性近似计算方程为:

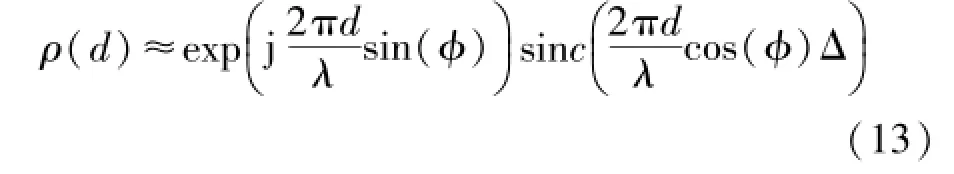
出于论文的目的定义sinc(x)=sin(x)/x。如果将σ=Δ/代入公式(13),可以比较功率谱高斯分布和均匀分布时分析结果如图6(φ=0和σ=2°)。结果显示波达信号功率谱在高斯分布中的波瓣减小速度更慢,且缺少次级相关性峰值点。另外众所周知ex还可以通过!来近似表达,同时sin(x)三角函数也可通过!来近似表达。因此在近似算法采用其前三项近似式,则在波达信号功率谱为高斯分布下,MIMO阵列两接收单元间信号衰落相关性式为:

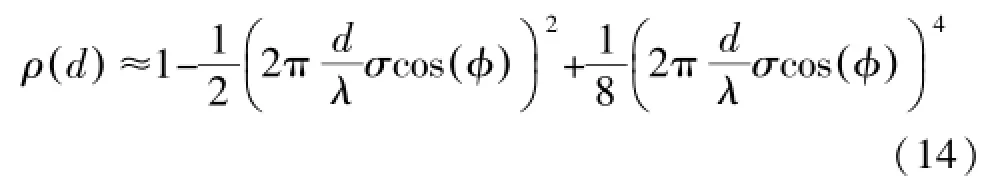
如果波达信号功率谱为均匀分布,其相关性式可为:

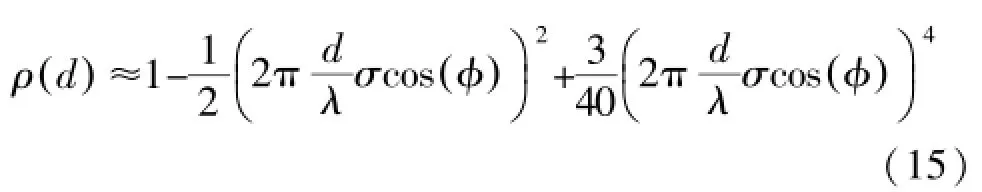
由于式(14)与(15)相关性公式是相似的,因此可以提出用式(3)来近似功率谱为高斯分布和均匀分布下的接收信号衰落相关性。另外也可采用其他常用功率谱分布函数,如拉普拉斯分布函数[16]。其拉普拉斯分布函数定义为:

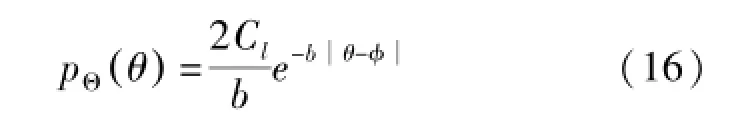
式中b是一个正常数,Cl是密度函数归一化常数。φ是波达信号中心到达角AOA。

2 组合分布下的MIMO衰落相关性理论

MIMO多天线接收信号衰落相关性系数作为天线参数的函数主要取决于信号到达角的功率谱和天线的信号发射模式。在实际无线通信环境中,由于存在电磁波信号的反射物体,多天线MIMO系统性能受空间信号相关性影响较大。空间相关性计算依赖于波达信号角AOA、信号功率普结构以及天线阵列单元排列结构等因素影响,且由于复杂无线环境使信道可能出现如图1所示的多反射簇以形成组合波达信号分布。

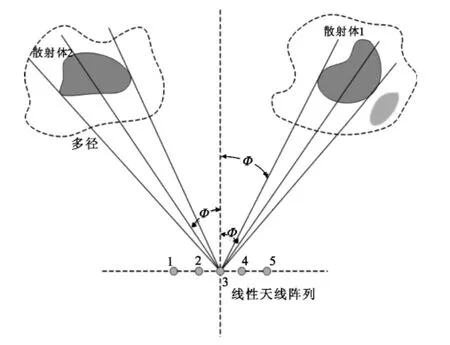
图1 MIMO阵列与组合波达信号功率谱Fig.1 MIMO array and combined signal power spectrum

2.1 组合功率谱高斯分布的信号衰落相关性

电波传播发射物分布集中在多个方位就可能使信道传播的波达信号分布形成多种功率谱和多个波达信号AOA。如存在两种波达信号分布时,可假设其波达信号功率谱分布是两个高斯分布的总和或者其它分布的组合以达到精确模拟各种信道环境。其联合分布函数可为:

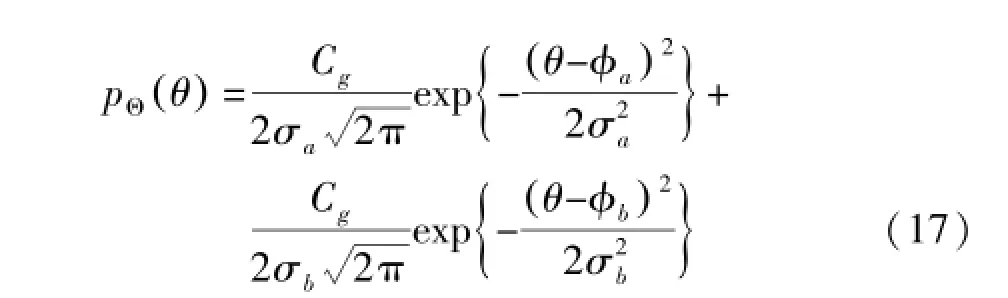
式中φa和φb是两个独立分布,σa和σb是高斯角能量分布下两个波达信号入射角的中心到达角AOA的标准差。Cg=1/erf(π/σg)是密度归一化常数。根据式(17),由前章节导出理论可得到在两种波达信号高斯功率谱分布下,MIMO阵列两天线阵元间接收信号衰落相关性式为:

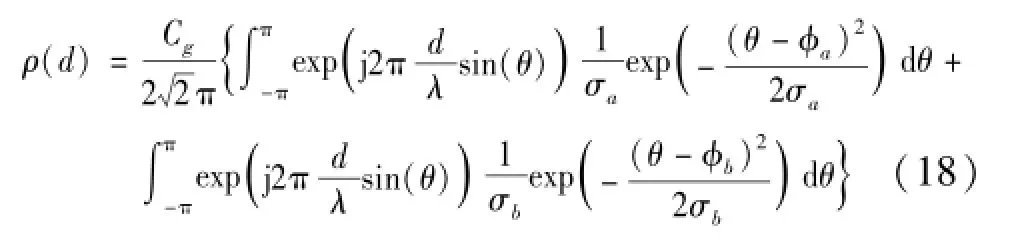
2.2 组合功率谱均匀分布的信号衰落相关性

同样针对组合功率谱为均匀分布时,可定义其功率谱分布函数为:

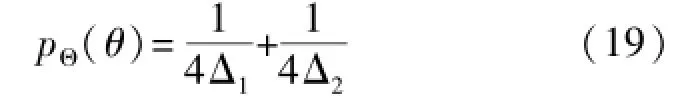
根据分布函数式(19),可以得到MIMO多天线阵列任意两单元间的接收信号衰落相关性为:

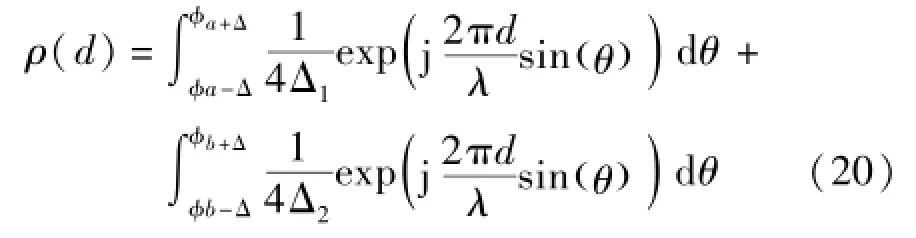
代入式(9)和(13)以及(14)和(15),可分别得到在组合功率谱为高斯分布和均匀分布时,导出MIMO多天线阵列任意两单元间接收信号相关性的理论近似表达式。

3 数值结果与分析

根据以上导出式可以得出MIMO多天线接收信号空间相关性是一个空间天线阵元间距为d,波达信号的功率谱分布与到达角为θ的阵列函数。图2 -3示在不同的波达信号到达角φ对均匀角功率谱分布下的信号衰落相关性分布的影响。从图2中可以发现当φ=60°时,σ与d/λ为变量的均匀功率谱分布对于空间相关性的关系。从图2中还可发现随着阵元之间距离的增加,信号衰落空间相关性呈现下降趋势,且随着σ的增大,相关性也迅速减小。从图3中可以发现当φ=45°时随着σ的增大,变化出现更多的副瓣。在比较图2和图3,在相同的天线距离内如果σ的逐渐增大使得接收信号空间相关性逐渐减小,随着信号到达角φ的减小与天线距离的不断增大,使得信号衰落空间相关性越小。

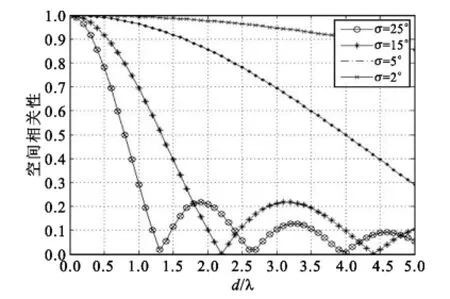
图2 φ=60°时功率谱均匀分布下MIMO间距为d/λ阵元接收信号衰落相关性Fig.2φ=60°the power spectrum of uniform distribution of MIMO space distanced/λarray signal fading correlation

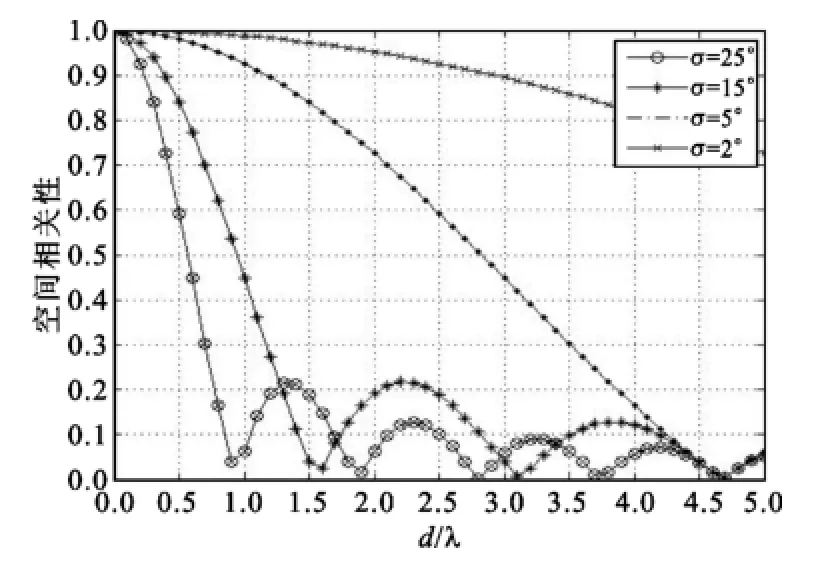
图3 φ=45°时功率谱均匀分布下MIMO间距为d/λ阵元接收信号衰落相关性Fig.3φ=45°the power spectrum of uniform distribution of MIMO space distanced/λarray signal fading correlation

图4-5示在不同的波达信号到达角φ对高斯角功率谱分布下的信号空间衰落相关性分布的影响。从图中可以发现当φ=60°时随着天线阵元间距的增大,空间相关性逐渐下降,且当σ逐渐增大时信号空间相关性逐渐减小。从图中还可以发现当波达信号到达角φ减小时,其空间相关性会逐渐减小。

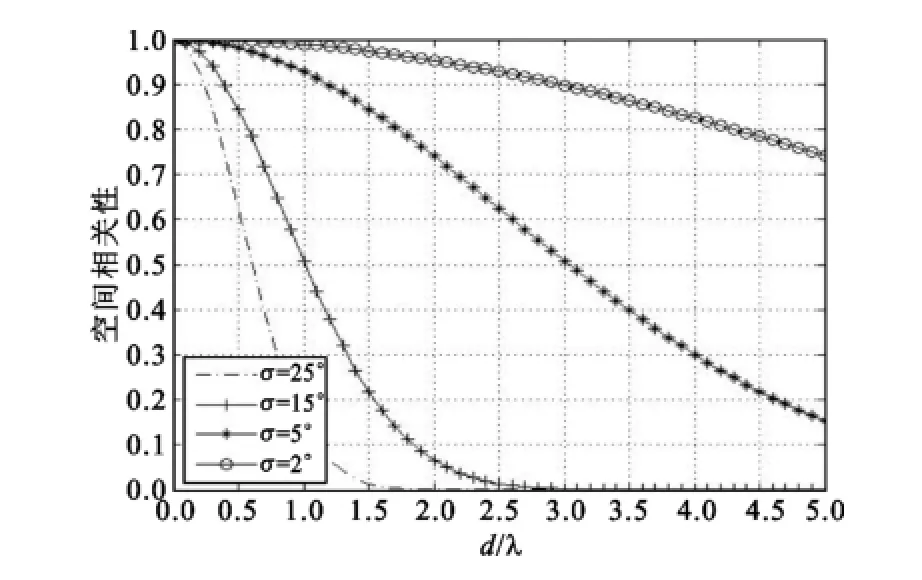
图5 φ=45°时功率谱高斯分布下MIMO间距为d/λ阵元接收信号衰落相关性Fig.5φ=45°the power spectrum of Gaussian distribution of MIMO space distanced/λarray signal fading correlation

图6-7示在2πσd/λ、功率谱角度扩展从低到高对于MIMO两个天线间在多种分布下的接收信号空间衰落相关性的影响。其中假设φ=0°和σ= {2°,20°},并用数值积分以得近似结果。从图中可以发现,对于相同的阵元间距和功率谱角度扩展来说谱分布越窄相关性越高。根据近似效果可以发现,对于两种分布以及σ所有的实际值,可用通用公式来表示。比较图6与图7可以发现,功率谱角度扩展的差异比较大,但仿真结果图形相近。仿真结果表明对于每种情况来说近似计算效果都非常好。在功率谱高斯分布(较高的相关性)的近似效果最好,对于均匀分布(较低的相关性)则相对较差。另外从图中发现仿真结果符合推论,高斯角功率谱分布的近似非常精确。综上所述通过公式(3)得到近似值的过程中假设σ的值是小的,可以预测对于更高的σ来说近似效果将会变差。从图7中可以看出结果与定性分析吻合。在其他情况时可怀疑当φ的值远大于0时近似效果可能将会变差。

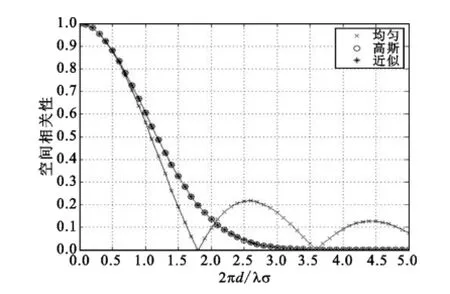
图6 σ=2°,φ=0°时功率谱均匀和高斯分布下MIMO阵列参数2πσd/λ阵元接收信号衰落相关性Fig.6σ=2°,φ=0°the power spectrum of uniform and Gauss distribution of MIMO array parameter array signal fading correlation

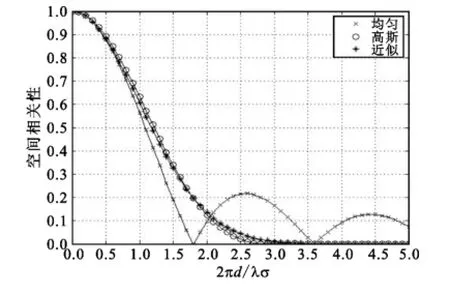
图7 σ=20°,φ=0°时功率谱均匀和高斯分布下MIMO阵列参数2πσd/λ阵元接收信号衰落相关性Fig.7σ=2°,φ=0°the power spectrum of uniform and Gauss distribution of MIMO array parameter array signal fading correlation

图8示在功率谱角能量分布对于σ=10°,φ= 60°时的空间相关性及近似分析结果比较。从图8可以发现其近似效果不理想。近似的精确性在φ超过60°的时候下降,但是由于大部分室外无线系统使用扇区(120°扇区),通常不需要考虑角度超过±60°的情况。从图8中还可以发现近似效果在高相关性值的时候最好,在低相关性值时效果最差。因为接收信号在高相关性值时比低相关性值更影响MIMO多天线阵列的性能。根据以上结论可以发现一个多天线阵列在相关性值1和0.5之间有比较大的性能差,在相关性值0.5和0之间性能差异很小[17]。

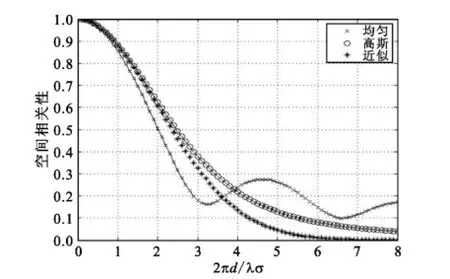
图8 σ=10°,φ=60°时功率谱均匀和高斯分布下MIMO阵列参数2πσd/λ阵元接收信号衰落相关性Fig.8σ=10°,φ=60°the power spectrum of uniform and Gauss distribution of MIMO array parameter array signal fading correlation

几种功率谱角能量分布下的MIMO多天线单元接收信号的衰落性能非常接近使用近似预测的性能结果。发现性能的主要决定因素(从多样性的角度)是功率谱角度扩展。

图9示在σa=σb=20°,φa=30°和φb=-30°时d/λ对于组合功率谱角能量分布的MIMO接收信号空间衰落相关性的影响。从图中可发现在计算组合分布的方差时用公式(3)有着可用这种测量方差将在相关性公式中提供第一波瓣的近似现象。从图中还可以发现,根据单边分布的这种情况,可以发现组合双边功率谱分布可以使用简单近似式。近似式适用于广范围的波达信号到达角功率谱分布和经典的角度扩展σ情况。另外在例子中假设波达信号对称中心到达角φa=-φb和σa=σb,当这两个条件都被违反时仿真结果均证明公式依然成立有效。

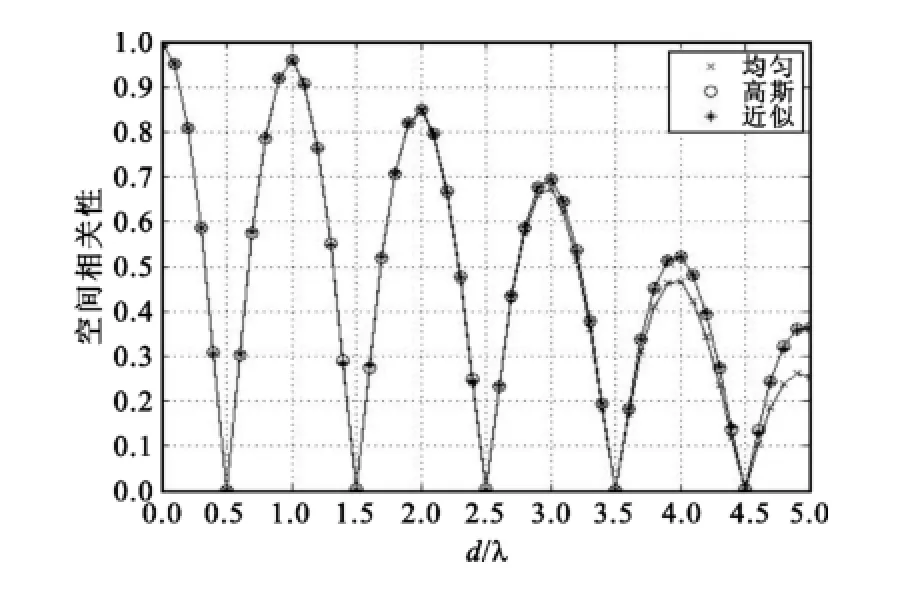
图9 σa=σb=20°,φa=30°,σb=-30°时功率谱均匀和高斯分布下MIMO阵列参数d/λ阵元接收信号衰落相关性Fig.9σa=σb=20°,φa=30°,σb=-30°array signal fading correlation versusd/λfor power spectrum of uniform, Gaussian distributions and proposed approximation

图10示为在σa=2°,σb=20°,φa=-30°和φb= 30°,即功率谱角能量服从组合双边分布时,空间参数2πd/λσ对MIMO多天线接收信号空间相关性的影响。图11示在功率谱角能量服从双边分布,不同波达信号参数与2πd/λσ对空间相关性的影响。

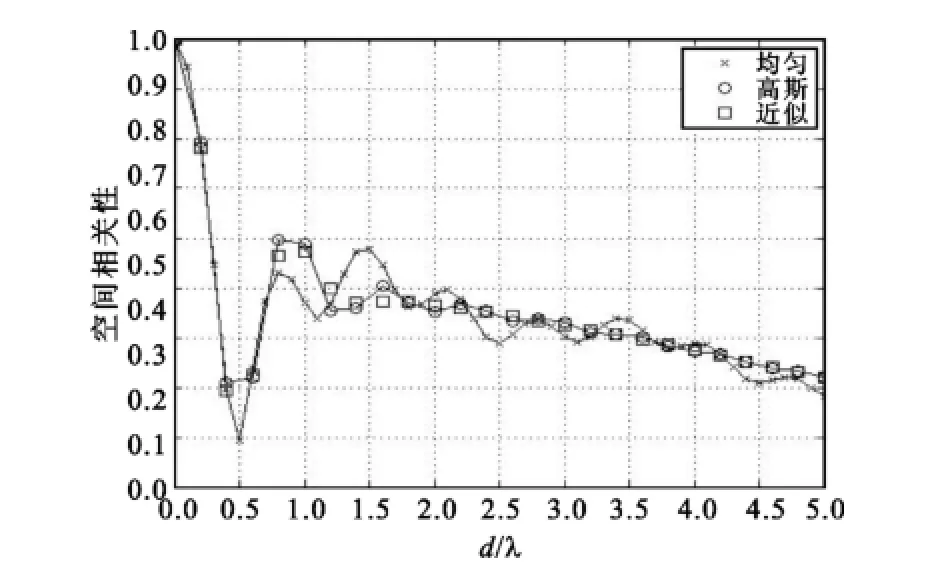
图10 σa=2°,σb=20°,φa=-30°,σb=30°时功率谱均匀和高斯分布下MIMO阵列参数d/λ阵元接收信号衰落相关性Fig.10σa=2°,σb=20°,φa=-30°,σb=30°array signal fading correlation versusd/λfor power spectrum of uniform,Gaussian distributions and proposed approximation

图10和图11表明功率谱角能量服从组合双边功率谱分布时的MIMO信号空间相关性同样符合文中单边分布情况下的推论,可用通用公式达到对多种组合功率谱分布进行分析和近似。另外较于单边分布时的情况,随着d/λ的增加组合功率谱分布下的MIMO多天线接收信号空间衰落相关性可出现更多的副瓣情况,使得在设计和优化MIMO多天线阵列需要更加慎重和选择阵列空间结构。

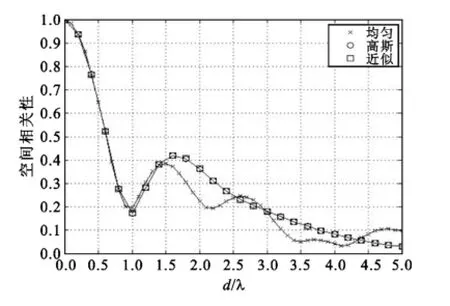
图11 σa=5°,σb=10°,φa=-30°时功率谱均匀和高斯分布下MIMO阵列参数d/λ阵元接收信号衰落相关性Fig.11σa=5°,σb=10°,φa=-30°array signal fading correlation versusd/λfor power spectrum of uniform, Gaussian distributions and proposed approximation

4 结 语

本文推导波达信号功率谱对MIMO信号接收衰落相关性通用式,研究组合功率谱分布下接收信号空间衰落相关性的广义近似式(即对于σ的多个值以及宽范围的到达角分布),并分析了在各种功率谱分布下的接收信号衰落相关性。结果证明分析方法可以很好地应用于波达信号功率谱为高斯分布、拉普拉斯分布和均匀角分布时的衰落信道情况。在功率谱分布是组合功率谱双边分布时,导出了接收信号衰落相关性特征。分析发现功率谱分布的标准偏差或角度扩展大小是确定接收信号衰落相关性的主导因素[18-19]。结果显示近似算法可用以准确地分析和仿真系统误码率性能,其分析效率更高。算法式同样可以被用于分析其他组合多边波达信号以及多种功率谱分布下的MIMO多天线阵列接收信号衰落相关性参数。

[1] JAKES W C.Microwave Mobile Communications[M]. New York:Wiley,1974.

[2] PROAKIS J G.Digital Communications[M].New York: McGraw Hill,1995.

[3] LEE W C Y.Effects of Correlation between Two MobileRadio Base-Station Antennas[J].IEEE Transactions on Communications,1973,21(11):1214-1223.

[4] SALZ J,WINTERS J H.Effect of Fading Correlation on Adaptive Arrays in Digital Communications[J].In Proceedings of the International Conference on Communications,1993(05):1768-1774.

[5] TSAN M W,CHIA M K.3-D Space-Time-Frequency Correlation Functions of Mobile-to-Mobile Radio Channels[J].IEEE Vehicular Technology Conference,2007 (65):334-338.

[6] 王健康.无线通信系统中MIMO技术的研究[D].北京:北京邮电大学图书馆,2004.

WANG Jian-kang.Study on MIMO Technology in Wireless Communication System[D].Beijing:Beijing University of Posts and Telecommunications library,2004.

[7] 陈靖峰,周杰.角能量分布及互耦效应对MIMO天线系统性能影响的研究[D].南京:南京信息工程大学图书馆,2012.

CHEN Jing-feng,Zhou J.Study on the Effect of the Angular Energy Distribution and the Effect of Mutual Coupling on the Performance of the MIMO Antenna System [D].Nanjing:Nanjing University of Information Science and Technology library,2012.

[8] 江浩,周杰.室内外非对称信道模型及其MIMO研究[J].安徽大学学报(自然科学版),2013(05):51-59.

JIANG H,Zhou J.Study of Asymmetric Geometrical Channel Models for Indoor and Outdoor Propagation Environments and its MIMO[J].Journal of Anhui University (NATURAL SCIENCE EDITION),2013(05):51-59.

[9] 王钢飞,石慧,卓东风.一种改进的MIMO-OFDM的信道估计算法[J].通信技术,2011(04):43-44.

Wang G F,Shi H,Zhuo D F.A Modified Channel Estimation Method for MIMO-OFDM System[J].Communications Technology,2011(04):43-44.

[10] 许少峰.阵列相关性对MIMO系统容量的影响[D].西安:西安电子科技大学图书馆,2005.

Xu Shao Feng.The Effect of Correlation between Array Elements on MIMO System Capacity[D].Xi′an:Xi′an Electronic and Science University Library,2005.

[11] 王莹,张平.无线资源管理[M].北京:北京邮电大学出版社,2005.

Wang Ying,Zhang Ping.Radio Resource Management [M].Beijing:Beijing University of Posts and Telecommunications Press,2005.

[12] 罗涛,乐光新.多天线无线通信原理与应用[M].北京:北京邮电大学出版社,2005.

Luo Tao,Yue Guang Xin.The Principle and Application of Multiple Antenna Wireless Communication[M]. Beijing:Beijing University of Posts and Telecommunications press,2005.

[13] ZHOU J,DONG L J,LI Y.Key Technologies for Hierarchical CDMA Cellular Wireless System[M].Beijing: China Meteorological Press,2009.

[14] JAKES W C.Microwave Mobile Communications[M]. New York:Wiley Inter science,1974.

[15] ZHOU J,SASAKI S,MURAMATSU S.Spatial Correlation Functions for a Circular Antenna Array and Their Applications in Wireless Communication System[J].IEICE Trans FUNDAM COMPUT SCI,2003,E86-A(7): 1716-1723.

[16] EGGERS P C F.Angular Propagation Descriptions Relevant for Base Station Adaptive Antenna Operations[J]. Wireless Personal Communications,1999(11):3-29.

[17] 姜金富,何海浪.MIMO-OFDM信道估计仿真实现[J].通信技术,2010(07):52-53.

Jiang J F,He H L.Simulation Realization of MIMOOFDM Channel Estimation[J].Communications Technology,2010(07):52-53.

[18] 李云,周杰.无线通信中的空时分组码性能研究[D].南京:南京信息工程大学图书馆,2010.

Li Yun,Zhou Jie.Study on the Performance of Packet Radio Communication Codes in Space-Time[D].Nanjing:Nanjing University of Information Science and Technology library,2010.

[19] 陈洪涛,周杰.快衰落信道下级联空时分组编码的研究[D].南京:南京信息工程大学图书馆,2010.

Chen Hong Tao,Zhou Jie.Research on Channel Concatenated Space Time Block Code Fast Fading[D]. Nanjing:Nanjing University of Information Science and Technology library,2010.

ZHOU Jie(1964-),male,Ph.D.,professor,mainly engaged in mobile communication,wireless sensor network and wireless access network.

刘 鹏(1990—),男,硕士研究生,主要研究方向为移动通信理论、无线传感网;

LIU Peng(1990-),male,graduate student,mainly engaged in mobile communication and wireless sensor network.

菊池久和(1951—),男,博士,教授,主要研究方向为信号处理和通信理论。

Hisakazu Kikuchi(1951-),male,Ph.D.,professor, mainly engaged in signal processing and communication theory.

Influence of Signal Power Spectrum Distribution on Signal Fading Correlation

ZHOU Jie1,2,LIU Peng1,Hisakazu Kikuchi2
(1.Dept.of Communications,Nanjing University of Information Science and Technology, Nanjing Jiangsu,210044,China;2.Dept.of Electronic and Electrical Engineering, Niigata University,Niigata 950-2181,Japan)

This paper deduces arrival signal power spectrum for MIMO(Multiple Input Multiple Output) multi-antenna signal reception fading correlation common type and analyzes the received signal correlation distribution of various power spectrums.Results show that the analysis can be applied to the channel when arrival signal power spectrum is in Gauss distribution,Laplace distribution or uniform angle distribution. When the power spectrum distribution is bi-modal,the received signal fading correlation characteristics are also deduced.The analysis results show that the standard deviation of power spectrum distribution or size of spread angle is the dominant factor of signal fading correlation.Numerical results indicate that the increase of distance between antenna-array and standard deviation of power spectrum distribution can reduce fading correlation of antenna-array receiving signal within a certain range and improve the performance of the system.Between antenna-array elements within long distance,power spectrum of Gauss distribution is more practicable and beneficial to analyzing and improving the performance of wireless channel multi-antenna MIMO system.

signal power spectrum;signal fading correlation;electromagnetic propagation;bi-modal distribution

TN911.6

A

1002-0802(2014)10-1114-07

10.3969/j.issn.1002-0802.2014.10.002

周 杰(1964—),男,博士,教授,主要研究方向为移动通信理论、无线传感网和无线接入网;

2014-08-12;

2014-09-12 Received date：2014-05-25;Revised date：2014-07-25

国家自然科学基金面上项目(No.61372128);江苏省科技支撑计划(工业)项目(BE2011195)

Foundation Item:National Natural Science Foundation of China(No.61372128);Scientific and Technological Support Project(Industry)of Jiangsu Province(No.BE2011195)