一类四元数矩阵保左特征值的线性映射条件*

袁 庚

(青岛科技大学数理学院，山东 青岛 266061)

引言

关于四元数及其左右特征值的研究，文献[1]中作了很多详尽而有系统的综述，到了目前为止关于四元数矩阵右特征值的研究已有很多令人满意的结果.1989年Bunse-Gerstener等在文献[2]中给出了四元数的QR分解和Schur分解，从而得到该四元数矩阵的右特征值和右特征值向量.

但四元数矩阵的左特征值所得结果较少.1985年，Wood在文献[3]用拓扑学的方法证明了四元数方阵的左特征值总是存在的，但并没有给出左特征值的计算方法.直到2001年，黄礼平和So Wasin在文献[4]中给出了二阶四元数矩阵左特征值的性质以及它们的代数表达式,但这远远不能满足我们的需要.

由于一般四元数的乘法不满足交换律，致使一般四元数行列式的定义便得十分困难，这更加深了我们对左特征值研究的难度.1991年，陈玄龙在文献[5]中首先提出了四元数重行列式的概念，并建立了重行列式理论.

设Q表示四元数集合，Mn(Q)表示n×n四元数矩阵的集合，则有：

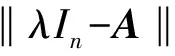
本文讨论以下问题：

如果M、N分别是下三角可逆四元数矩阵且线性映射φ：Mn(Q)→Mn(Q)满足φ(A)=MAN, 当φ(A)与A具有相同的左特征值，则M和N中的元素满足什么条件？

本文证明了下面的结果：

定理2如果M、N∈Mn(Q)分别是下三角可逆四元数矩阵且线性映射φ：Mn(Q)→Mn(Q)满足φ(A)=MAN，对于任意下三角四元数矩阵A∈Mn(Q)，φ(A)与A具有相同的左特征值当且仅当M和N中的元素mss,nss分别与A中的元素ass的虚部对应成比例且mssnss=1，或虚部对应为零.

1 定理2的证明

1.1 辅助引理

为证明定理2，首先给出一些辅助结果.

引理2 若ab=ba，则a与b的虚部对应成比例，或虚部对应为零.

证明设a=a1+a2i+a3j+a4k，b=b1+b2i+b3j+b4k，则：

ba=(a1b1-a2b2-a3b3-a4b4)+(a1b2+a2b1+a4b3-a3b4)i+

(a1b3+a3b1+a2b4-a4b2)j+(a1b4+a4b1+a3b2-a2b3)k，

ab=(a1b1-a2b2-a3b3-a4b4)+(a1b2+a2b1+a3b4-a4b3)i+

(a1b3+a3b1+a4b2-a2b4)j+(a1b4+a4b1+a2b3-a3b2)k.

若ab=ba，则：

a1b1-a2b2-a3b3-a4b4=a1b1-a2b2-a3b3-a4b4;

a1b2+a2b1+a3b4-a4b3=a1b2+a2b1+a4b3-a3b4;

a1b3+a3b1+a4b2-a2b4=a1b3+a3b1+a2b4-a4b2;

a1b4+a4b1+a2b3-a3b2=a1b4+a4b1+a3b2-a2b3.

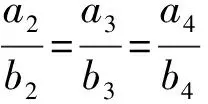
引理3 若a=man，则m,n与a的虚部对应成比例，且mn=1.

证明若a=man，则：m-1a=an.设：

m-1=m1+m2i+m3j+m4k，

a=a1+a2i+a3j+a4k，

n=n1+n2i+n3j+n4k

则：

m-1a=(a1m1-a2m2-a3m3-a4m4)+(a1m2+a2m1+a4m3-a3m4)i+

(a1m3+a3m1+a2m4-a4m2)j+(a1m4+a4m1+a3m2-a2m3)k，

an=(a1n1-a2n2-a3n3-a4n4)+(a1n2+a2n1+a3n4-a4n3)i+

(a1n3+a3n1+a4n2-a2n4)j+(a1n4+a4n1+a2n3-a3n2)k.

由m-1a与an的实部相等，可得到：

a1m1-a2m2-a3m3-a4m4=a1n1-a2n2-a3n3-a4n4

即：

a1(m1-n1)-a2(m2-n2)-a3(m3-n3)-a4(m4-n4)=0

因为a1,a2,a3,a4不全为零，故m1=n1,m2=n2,m3=n3,m4=n4.

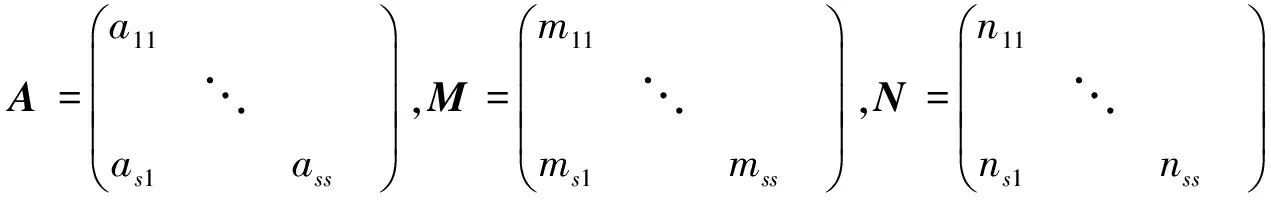
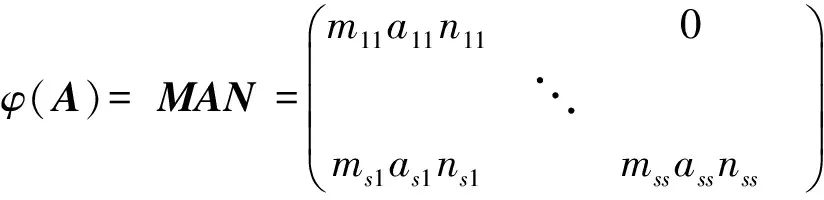
1.2 定理2的证明

1)必要性证明

若λ为A的左特征值，φ(λ)为φ(A)的左特征值, 则：

从而得到λ=att(t=1,2,3,…s)，即A的左特征值为它的对角线元素.

又因为mss,nss与A中ass的虚部对应成比例，且mssnss=1，由引理3得mssassnss=ass.

故φ(λ)=att，(t=1,2,…s).即λ也是φ(A)的左特征值，因此φ(A)与A具有相同的对角线元素，φ(A)与A具有相同的左特征值.

2)充分性证明

因为φ(A)与A具有相同的左特征值，且两者均为三角阵，结合引理1与引理4，两者具有相同的对角线元素.不失一般性，我们认为mssassnss=ass.结合引理3，mss,nss与A中ass的虚部对应成比例且msns=1，或虚部对应为零.

2 结语

本文讨论了三角形四元数矩阵形如映射φ(A)=MAN保左特征值的条件，这个结果，有利于提高复杂四元数矩阵左特征值的计算效率，同时也有益于一般四元数矩阵的左特征值问题的研究.

参考文献:

[1]Zhang Fuzhen. Quaternion and Matrices of Quaternions [J]. Linear Algebra and Its Application ，1997，251:21-57.

[2]Bunse-GerstuerA,ByersR,MehrmannV.AQuaternionQRAlgorithm[J].Numer.Math, 1989, 55: 83 -95.

[3]WoodRMW.QuaternionicEigrnvalues[J].Bull.Londonmath,Soc, 1985, 17:137-138.

[4]HuangLiping,WasinS.OntheEigenvaluesofaQuaternionicMatrix[J].LinearAlgebraandItsApplication, 2001, 323:105-116.

[5]ChenLongxuan.DefinitionofDeterminantandCramerSolutionsovertheQuaternion[J].Field.ActaMath,Sinica,NewSeries, 1991, 7(2):171-180.