舰船复合材料夹层板架结构的分级递进优化设计方法

周晓松，梅志远

海军工程大学舰船工程系，湖北武汉430033

0 引 言

板架结构具有承载能力强、重量轻的特点，被广泛用于船舶结构，且随着复合材料在舰船结构上的应用，也得到了越来越广泛的关注。对复合材料板架结构开展优化设计方法应用基础研究，有利于科学、合理地评价舰船复合材料结构的优越性，具有重要的工程价值和理论意义。

复合材料板架结构由于具有各向异性，且界面复杂、可设计变量众多，因而优化设计难度大，而传统的数学规划法或准则法却很难解决此类问题。近年来，国内外学者对此开展了广泛的研究。吴莉莉等［1］提出了加筋板稳定性约束下的二级协同优化算法。乔巍等［2］采用等效弯曲刚度法实现了铺层顺序的优化。赵群等［3］提出了基于压弯刚度复合材料加筋板的布局优化设计方法。李烁等［4］应用神经网络对复合材料帽形筋加筋板进行了优化。张铁亮等［5］采用试验设计建立了代理模型方法。刘克龙等［6］在对机翼的气动结构进行多学科优化设计时运用了低自由度协同优化方法。Blair 等［7］将快速建模方法应用到了翼面结构的布局优化设计中。Nagendra 等［8］应用改进的遗传算法对加筋板结构进行了优化设计。

本文将采用分级递进优化设计方法，对复合材料板架结构的设计变量进行系统分解，通过对子系统的递进优化和相互协调，解决舰船工程实践［9］中复合材料板架结构的多变量设计问题。

1 典型板架结构强度特性的仿真分析

1.1 典型板架结构仿真分析模型的建立

本文针对某型舰上层建筑甲板室舷侧外侧壁夹层板架建立初始计算模型，展开强度特性分析，建模采用的单位制为kg，mm 和s。板架由夹层板、4 根横筋和4 根纵筋构成。夹层板由上、下玻璃钢表层和PVC 泡沫芯材组成；筋材为帽形筋结构，包括内部芯材与玻璃钢表层。板架尺寸参数如表1 和图1～图3 所示。

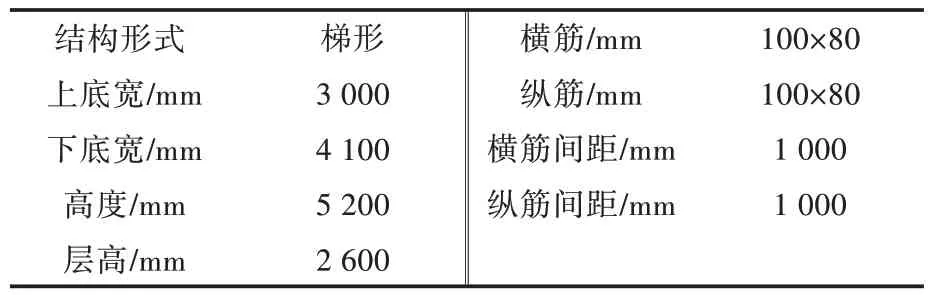
表1 板架尺寸参数Tab.1 Dimension parameters of stiffened panel

图1 结构布置图Fig.1 Structural layout

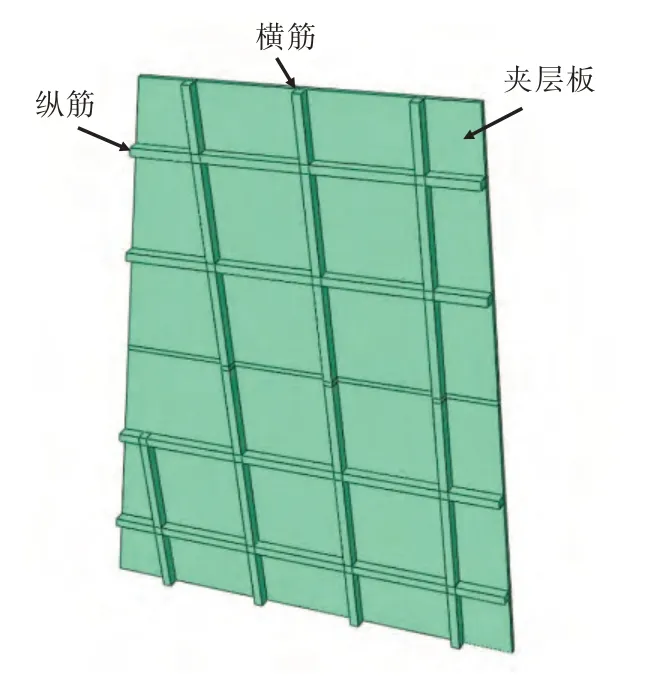
图2 构件示意图Fig.2 Schematic diagram of structural components

图3 局部截面示意图Fig.3 Schematic diagram of local section

板架初始计算模型的边界条件：考虑板架最危险的承载工况，板架边界、板架与中间甲板相接处均设置固支约束。单元类型：基于材料的力学性能和结构的受力特征，玻璃钢采用Shell 单元，芯材采用Solid 单元进行建模。网格划分：对板架模型进行网格划分，全局种子密度为9；筋材相接区域的网格进一步细化，局部种子密度为6；板材厚度划分为6 层；网格数量为1 557 591。载荷：舷侧外侧壁板加载均布70 kPa 载荷。材料参数和板架初始计算模型如表2、表3 和图4 所示。

表2 材料参数（玻璃钢）Tab.2 Material parameters（glassfiber reinforced plastics）

表3 材料参数（PVC 泡沫芯材）Tab.3 Material parameters（PVC foam core）

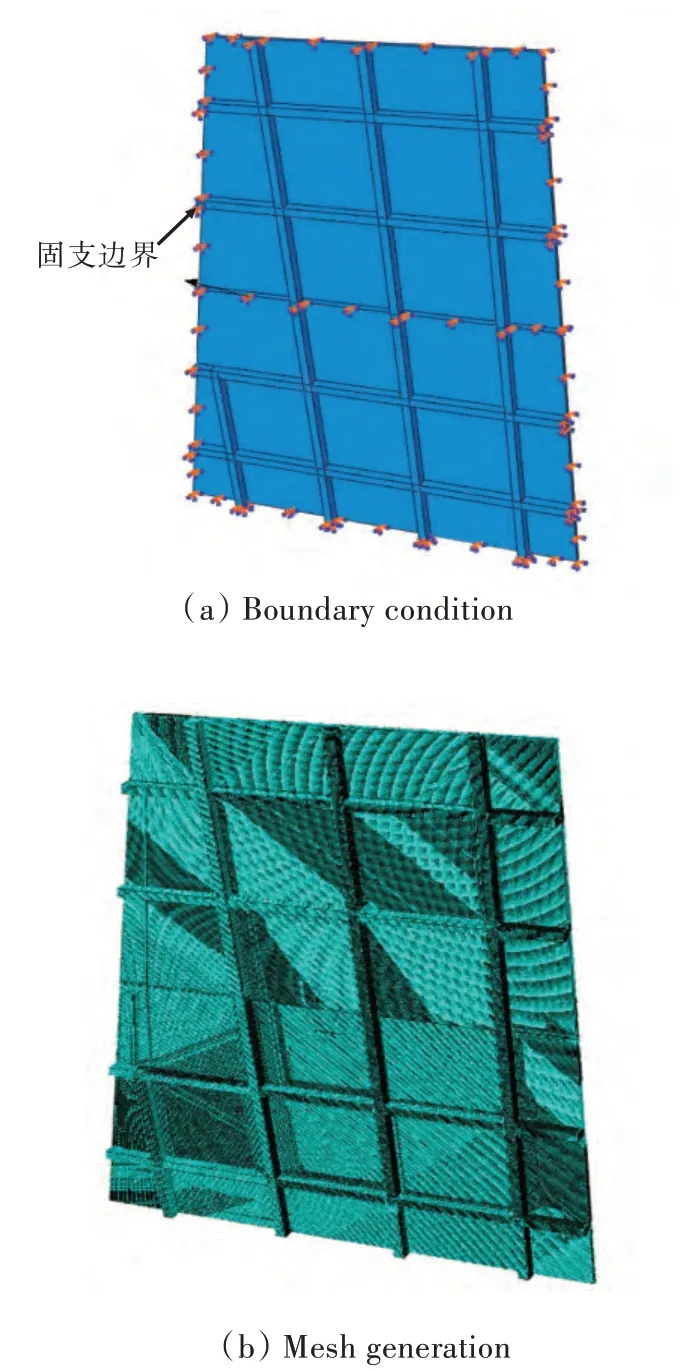
图4 板架初始计算模型Fig.4 Initial computational model of stiffened panel

1.2 计算结果

通过计算，得到舷侧外侧壁板架结构的位移云图和应力云图如图5～图7 所示，其中位移和应力单位分别为mm 和kPa。

分析计算结果可知，复合材料板架结构在均布载荷作用下的变形规律与钢质板架基本相同。玻璃钢的应力峰值为450.2 MPa，整体应力水平较低，约为80～220 MPa；芯材的应力峰值为2.29 MPa，整体应力水平约为0.8～1.5 MPa。

图5 位移云图Fig.5 Displacement contours

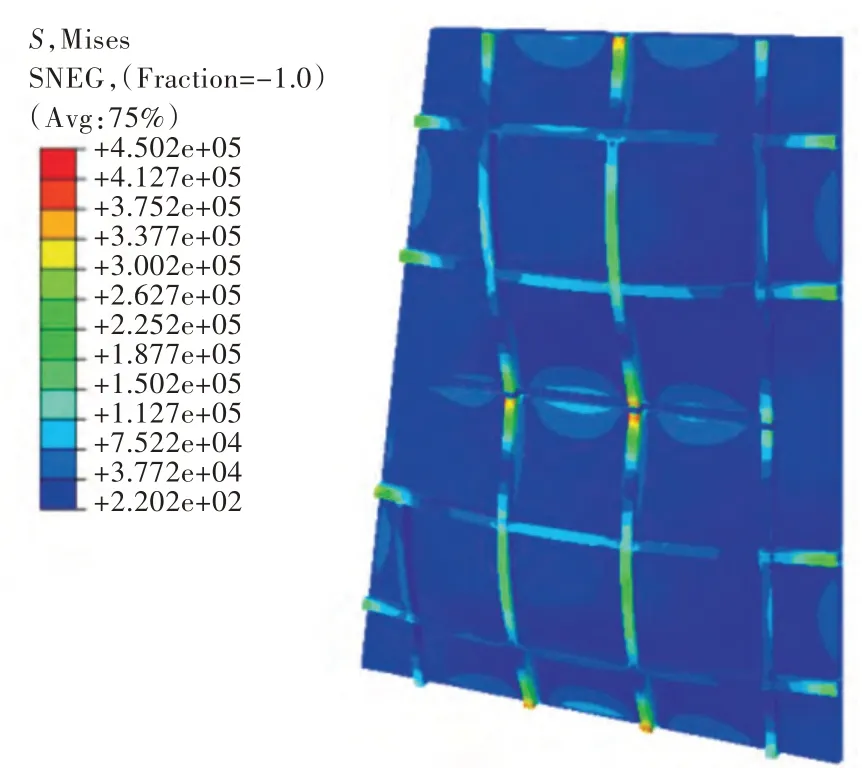
图6 玻璃钢应力云图Fig.6 Stress contours of glassfiber reinforced plastics

图7 芯材应力云图Fig.7 Stress contours of PVC foam core

由于板架结构建模对连接区域进行了简化，因而局部应力集中问题突出，主要集中在筋材相接区域和边界区域。在整体优化设计阶段，将仅以中心区域板格（去除边界板格与局部应力集中区域）的应力水平来评价板架的承载能力，局部连接结构与边界约束较强区域峰值过高的问题暂不予考虑，可通过局部结构细节设计和结构形式优化进行重点分析。板架结构质量为486 kg，质量较大，有必要通过优化来减轻质量，提高板架结构的承载效率。

板架结构的优化设计变量众多，包括夹层板芯材厚度、纵横加强筋截面尺寸、复合材料铺层厚度、复合材料铺层角度和铺层顺序，要想一次全部优化极为困难，需要对优化设计变量进行分析，采用分步优化的策略进行。

2 分级递进优化设计方法介绍

针对复合材料板架结构优化设计这个系统问题，采用了分级递进优化设计方法。该方法是将一个复杂的系统优化问题分解为若干较简单的子系统，通过对各子系统分别进行优化和级间协调来实现原系统的优化。各个子系统虽然相互关联，但又有其相对独立性，根据对使用功能、承载特点和结构形式的分析，若在独立性强、关联性弱的部位加以分解，只需很少几次迭代，就能收敛到满意的优化解。

对板架结构全部优化设计变量进行灵敏度分析，将优化设计变量分为2 类：第1 类为夹层板芯材厚度、加强筋芯材尺寸和表层玻璃钢厚度；第2类为给定角度下玻璃钢的铺层数量和铺层顺序。分析每类优化设计变量的特点，进而将板架优化工作分为宏观尺寸优化和铺层方式优化两级进行。该方法思路简明，实施方便，易于与常用的工程结构分析算法和强度衡准协调，并且还可降低所有优化设计变量一起优化所带来的耦合影响，从而达到最佳优化效果，如图8 所示。

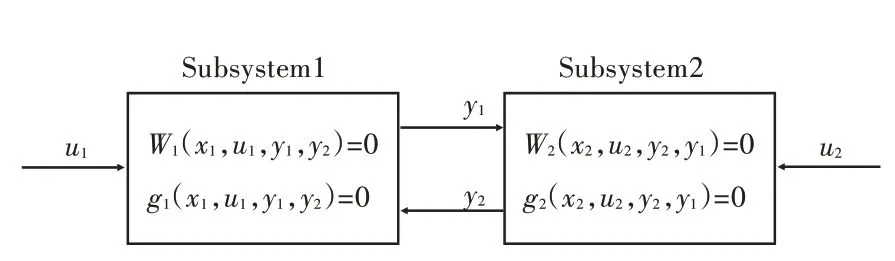
图8 二级系统示意图Fig.8 Schematic diagram of two-stage system

板架结构优化设计的数学模型可表述如下：

最小化优化目标函数

对于各子系统，状态变数Xi与输入、输出变数之间存在下述等式与不等式约束：

其中：Xi为子系统i 的状态变数，即板架结构使用材料的极限强度值；Ui为子系统i 的输入变数，即系统i 优化前的设计变量值；Yi为子系统i 的输出变数，即系统i 优化后的设计变量值，同时又是其他子系统的干涉变数。

目标函数被分离到每一个子系统，但由于存在相互联系的干涉变数，因而需要采用逐次迭代的方式来实现。首先，将干涉变数人为地加以固定，使各子系统完全被分割，即给定某一组变量Zi，并使Y=Z 。然后，在第1 级优化的基础上逐次修正干涉变数，使总目标函数取极值。因此，二级优化结构成为下述形式。

第1 级：

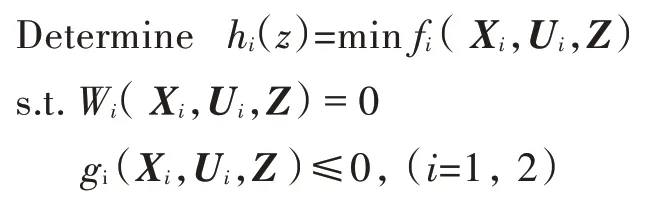
第2 级：

在求解时，首先给定干涉变数的一个初始估计值Z，在第1 级对每一个子系统分别进行优化，然后再将第1 级所得结果传递到第2 级，在第2 级通过目标函数h（Z）的最优化来修改Z，并最后确定其最优值。

2.1 一级优化分析

宏观尺寸优化阶段的数学模型可具体表述为：

最小化目标函数fi（u）

约束gi（u）gj

U≤0，（j=1，…，X）

其中：f （iu）为目标函数；g （iu）和gjU分别为第j 个约束响应和响应的上限值；X 为所有约束的数目；YE 为单元数目；Yp为一级优化设计变量的数目；uik为第k 个单元所在的第i 个一级优化设计变量的厚度，且设计变量的厚度是可以连续变化的。在宏观尺寸优化阶段，只考虑全局响应和非强制的工艺约束。本文中，此阶段考虑的全局响应包括静强度响应和质量响应，将静强度响应（即板架结构使用材料的极限强度值）作为约束，质量响应作为目标。非强制的工艺约束包括一级优化设计变量尺寸的设计范围，即优化后的板架构件尺寸值不大于初始板架构件尺寸。

2.2 二级优化分析

铺层方式优化可以进一步分为层组尺寸优化和铺层次序优化2 个步骤。

宏观尺寸优化的结果是复合材料铺层的总厚度。在层组尺寸优化设计中，同一方向和布局的多层被认为是一个层组，这可以在很大程度上减少层数，便于通过改变每个层组的厚度来模拟铺层的增加或减少。本文采用的铺层为垂直正交的纤维布，采用0°和45°铺层，从而可以将复合材料层合板以两级层组的形式进行建模。由于层组厚度可以独立变化，这种建模方式有利于强调层合板的优化位置及层组厚度，因而可以从最终的厚度优化中得到需要的铺层数。

层组尺寸优化后，铺层布局与铺层细节便均完成，但详细的工艺约束可能还不满足。因此，本阶段在满足所有设计约束的条件下，将对所有的铺层进行顺序优化，以满足所有的工艺约束。

3 典型板架结构优化实例分析

3.1 灵敏度分析

图9 设计变量灵敏度分析图Fig.9 Screenshot of design variable sensitivity

对上文建立的板架结构模型进行优化设计变量的灵敏度分析，其结果如图9 所示。通过分析结果，表明在初始板架结构模型分析中，夹层板芯材厚度对板架重量影响的灵敏度为58%；玻璃钢铺层厚度对板架的应力水平影响最大，灵敏度为32%；纵向加强筋尺寸对板架应力水平的影响大于横筋的，其灵敏度分别为29%和26%；其中纵筋高度和横筋宽度对板架应力水平的影响较大，灵敏度分别为23%和21%。综合分析所有优化设计变量后可知，夹层板芯材厚度、玻璃钢铺层厚度与加强筋芯材尺寸等宏观设计变量对优化目标的影响较大，而玻璃钢铺层角度和铺层顺序的影响则相对较小，因而可将复合材料板架结构优化分为宏观尺寸优化和铺层方式优化两级进行。

3.2 一级优化分析

在上层建筑结构设计中，质量是重要的设计指标，上层建筑结构质量的增加会导致舰船重心升高，从而影响舰船稳定性。因此，建立了以质量为目标函数，以静强度为约束条件，以夹层板芯材厚度、加强筋芯材截面尺寸和玻璃钢铺层厚度为一级优化设计变量的有限元优化模型，优化目标为板架结构质量最小。通过优化，确定夹层板芯材厚度、加强筋芯材截面尺寸和玻璃钢铺层厚度。

3.3 二级优化分析

本阶段需要综合所有的设计响应和工艺约束，确定规定角度下的铺层数量和铺层顺序。

层组尺寸优化阶段的模型与宏观尺寸优化阶段的相同，但优化设计变量变为了层组厚度，并且增加了非强制的工艺约束条件。最终，确定复合材料各角度层组的厚度和铺层数量，进而得到总的铺层数量。在整个层组尺寸优化过程中，所有的约束违反均为0%。层组尺寸优化后，将复合材料层组离散为由基本厚度为0.31 mm 铺层组成的不等厚的复合材料层合板。

在层组尺寸优化的基础上开展铺层次序优化，用以确定最终的铺层顺序。本阶段优化时的所有响应约束与层组优化阶段相同，但设置了更为详细的工艺约束，如外表面铺层使用45°的铺层，以提高抗剪能力；保证铺层数量和位置对称分布，减小制造过程中可能产生的应力；限制同一角度的铺层数量，以减小边缘分层现象的发生。优化后的复合材料铺层次序为【45/0/45/07/45/0/45】。

4 优化前、后结果比较分析

复合材料板架结构经过两级优化后，其位移云图、应力云图和质量比较分别如图10～图12 及表4、表5 所示。

图10 优化后的位移云图Fig.10 Displacement contours after optimization

图11 优化后的璃钢应力云图Fig.11 Stress contours of glass fiber reinforced plastics after optimization

图12 优化后的芯材应力云图Fig.12 Stress contours of PVC foam core after optimization

表4 复合材料优化前、后宏观尺寸比较Tab.4 Comparision of macroscopic size of composite materials before and after optimization

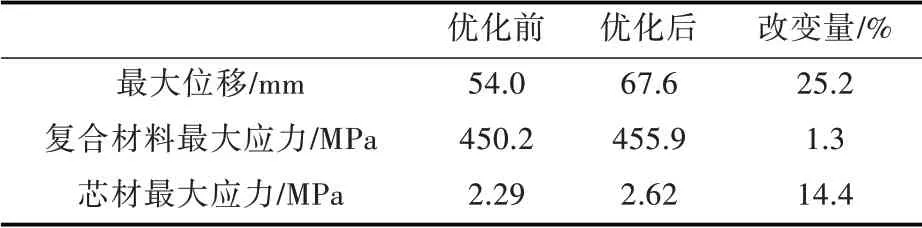
表5 板架结构优化前、后性能参数比较Tab.5 Comparision of performance parameters of stiffened panel before and after optimization

通过优化，夹层板芯材厚度由40 mm 减少至32 mm，减少了20%；玻璃钢厚度由5 mm 减至4 mm，减少了20%；板架结构总质量从486 kg 减轻至391 kg，减轻了19.5%，减重效果明显。其中横筋尺寸相对于纵筋尺寸变化较小，表明在板架结构中横筋所起的承载作用更大。优化后，结构的最大位移及最大应力与优化前相比均增大，边界约束区域的应力峰值已达到材料的强度极限，但仍满足板架结构的设计约束要求。在此处，可只关注整体板架的承载能力，局部连接结构与边界约束较强区域峰值过高的问题暂不予考虑，应通过局部结构细节设计和结构形式优化予以重点分析。

5 结 论

1）基于Isight 优化平台的分级递进优化设计方法能够满足复合材料夹层板架结构的优化设计要求，优化后，夹层板表层和芯材的应力水平趋向于约束要求值，能满足设计要求。

2）均布载荷作用下，对复合材料板架结构承载能力影响最大的设计变量为夹层板表层玻璃钢厚度和芯材厚度，其次为加强筋芯材尺寸。在复合材料板架结构优化设计中，应重点分析，提高优化效率。

3）采用0°和45°层组进行铺层，经宏观尺寸优化和铺层方式优化这两个阶段后，在满足板架结构强度要求的前提下，复合材料板架结构的质量从486 kg 下降到了391 kg，共减少95 kg，减重达19.5%，说明优化方法效率很高，且优化结果满足制造工艺要求，具有很高的工程应用价值。

4）文中板架的优化结果仅以中心区域板格的应力水平来评价整体板架的承载能力，是对板架模型进行简化后的优化结果，而对局部连接结构与边界约束较强区域峰值过高的问题则并未考虑，这可在下一步局部结构细节设计和结构形式优化时进行重点分析。

［1］吴莉莉，姚卫星.复合材料加筋板结构的二级协同优化设计方法［J］. 南京航空航天大学学报，2011，43（5）：645-649.WU Lili，YAO Weixing. Two-level collaborative opti⁃mum design method for composite stiffened panel［J］. Journal of Nanjing University of Aeronautics ＆Astronautics，2011，43（5）：645-649.

［2］乔巍，姚卫星.复合材料加筋板铺层优化设计的等效弯曲刚度法［J］.计算力学学报，2011，28（1）：158-162.QIAO Wei，YAO Weixing. Equivalent bending stiff⁃ness method for stacking sequence optimization of com⁃posite stiffened panel［J］. Chinese Journal of Computa⁃tional Mechanics，2011，28（1）：158-162.

［3］赵群，丁运亮，金海波. 一种基于复合材料加筋板结构效率的稳定性优化方法［J］.复合材料学报，2010，27（3）：169-176.ZHAO Qun，DING Yunliang，JIN Haibo . Buckling optimization method based on structure efficiency of composite stiffened panels［J］. Acta Materiae Composi⁃tae Sinica，2010，27（3）：169-176.

［4］李烁，徐元铭，张俊. 基于神经网络响应面的复合材料结构优化设计［J］. 复合材料学报，2005，22（5）：134-140.LI Shuo，XU Yuanming，ZHANG Jun. Composite structural optimization design based on neural network response surfaces［J］. Acta Materiae Compositae Sini⁃ca，2005，22（5）：134-140.

［5］张铁亮，丁运亮.复合材料加筋壁板的结构布局优化设计［J］. 南京航空航天大学学报，2010，42（1）：8-12.ZHANG Tieliang，DING Yunliang. Structural layout optimization of composite stiffened panel［J］. Journal of Nanjing University of Aeronautics ＆ Astronautics，2010，42（1）：8-12.

［6］刘克龙，姚卫星，余熊庆. 运用低自由度协同优化的机翼结构气动多学科设计优化［J］.航空学报，2007，28（5）：1025-1032.LIU Kelong，YAO Weixing，YU Xiongqing. Multidis⁃ciplinary structural-aerodynamic design optimization of wings with low degree-of-freedom collaborative opti⁃mization［J］. Acta Aeronautica et Astronautica Sinica，2007，28（5）：1025-1032.

［7］BLAIR M，HILL S，WEISSHAAR T A. Rapid modeling with innovative structural comcepts. AIAA-98-1755［R］. American Institute of Aeronautics and Astronau⁃tics，1998.

［8］NAGENDRA S，JESTIN D，GURDAL D，et al. Im⁃proved genetic algorithm for the design of stiffened composite panels［J］. Computers and Structures，1996，58（3）：543-555.

［9］MOURITZ A P，GELLERT E，BURCHILL P，et al.Review of advanced composite structures for naval ships and submarines［J］. Composite Structures，2001，53（1）：21-42.