多尺度的潜艇集体逃生舱运动过程数值模拟

唐鑫，黄祥兵，黄兴玲

海军工程大学舰船工程系,湖北武汉430033

0 引 言

目前，我国潜艇集体逃生舱的研究多处于理论研究阶段，对其进行模型试验的研究还较少［1］，仅在某型试验艇上装有小型逃生舱。建立可验证试验结果的计算机仿真模型有助于集体逃生舱模型试验阶段研究的开展。为此，本文将建立与模型试验相对应的计算机仿真模型，旨在对潜艇集体逃生舱的运动过程进行数值模拟，研究影响其运动过程的各项参数。同时，也有助于验证模型试验的结果，归纳、总结出对逃生舱的发展有帮助的规律和建议。本文主要研究尺度参数对逃生舱运动的影响规律。由于大开孔对潜艇的强度有影响，考虑到潜艇的总布置要求，须对集体逃生舱的尺度进行限制。本文集体逃生舱的尺寸将按照潜艇圆柱型耐压船体开孔结构的强度计算方法，遵循开孔率≤0.3 的标准来设计［2］。

1 潜艇集体逃生舱运动过程理论模型

建立如图1 所示的坐标系。坐标系原点为逃生舱的浮心，OX 轴指向逃生舱的顶部并与其对称轴重合，OY 轴与OX 轴垂直，OZ 轴由右手定则确定。

图1 坐标系图Fig.1 Coordinate System

1.1 潜艇集体逃生舱上浮运动理论模型

对集体逃生舱的上浮运动进行简化，只考虑纵向的运动，应用动量定理和动量矩定理［3］，根据集体逃生舱上浮运动的实际情况建立其纵向运动方程组，即为逃生舱上浮运动的理论模型：

式中：v 为集体逃生舱上浮的速度；wz为旋转角速度；L 为舱体长度；S 为中部横截面积；xg，yg为舱体重心的坐标；B为浮力；G为重力；Jzz为轴向惯性矩；分别为集体逃生舱的阻力系数、侧力系数和偏转力矩系数；分别为侧力系数和偏转力矩系数的旋转导数；λ11，λ22，λ26，λ66分别为集体逃生舱的附加质量；m为舱体质量。

1.2 潜艇集体逃生舱入水冲击理论模型

上节中的逃生舱上浮运动理论模型输出的集体逃生舱上浮速度v 是入水冲击模型中的输入，即v 为逃生舱冲击入水过程中的总体节点速度矢量U'(t)。本文采用ANSYS/ LS-DYNA 对集体逃生舱入水冲击进行模拟，在入水冲击过程中，通常把结构体用有限元离散化，其有限元方程可表示为［4］

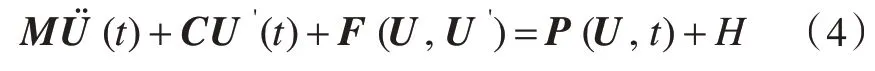
式中：M 为质量矩阵；C 为阻力矩阵；P 为总体冲击力矢量；F 为单元重力场等效节点力矢量组；H 为总体结构沙漏粘性阻尼力；(t)为总体节点加速度矢量；U'(t)为总体节点速度矢量；U 为总体节点位移矢量。

以上理论虽然能对集体逃生舱的上浮运动和入水冲击进行定性分析，但不能获得本文所要求的精确解。因此，需要通过有限元软件FLUENT 和ANSYS/LS-DYNA进行建模计算来得到精确解。

2 潜艇集体逃生舱数值仿真计算

2.1 潜艇集体逃生舱运动过程仿真模型的建立

潜艇集体逃生舱在释放之后，其运动过程分为3 个阶段：水下自由上浮、出水运动和入水冲击。文献［5］给出了结构体的出水过程，其速度是先增大后减小，最终使结构体的速度略有增加。本文将出水运动进行简化也能使计算结果偏于安全，并认定出水过程中集体逃生舱的速度不变。

潜艇集体逃生舱模型选取胶囊状球底舱体，中间为长圆柱，两端为半球壳体，厚度11 mm［6］。集体逃生舱垂直布置于潜艇中部，由此，逃生舱的直径就需要有所限制。考虑到大开孔对潜艇结构的影响，可以按照潜艇圆柱型耐压船体开孔结构的强度计算方法，按照开孔率（开孔半径/潜艇半径）≤0.3 的范围来设计集体逃生舱的直径，设本文建立的集体逃生舱的直径均符合以上要求。为研究尺度参数的影响规律，本文建立了5 个直径递增并且体积相等的逃生舱模型：（D，L）=（1.600，7.900），（1.800，6.868）,（2.000，6.000），（2.200，5.254），（2.400，4.596），其中D 为逃生舱圆球底的直径，L 为圆柱体部分的长度，单位均为m。建立的逃生舱上浮运动仿真模型和入水冲击仿真模型如图2 所示，基本参数如表1 所示。

2.2 潜艇集体逃生舱自由上浮运动数值模拟

2.2.1 计算思路

图2 集体逃生舱模型图Fig.2 Models of escape capsule

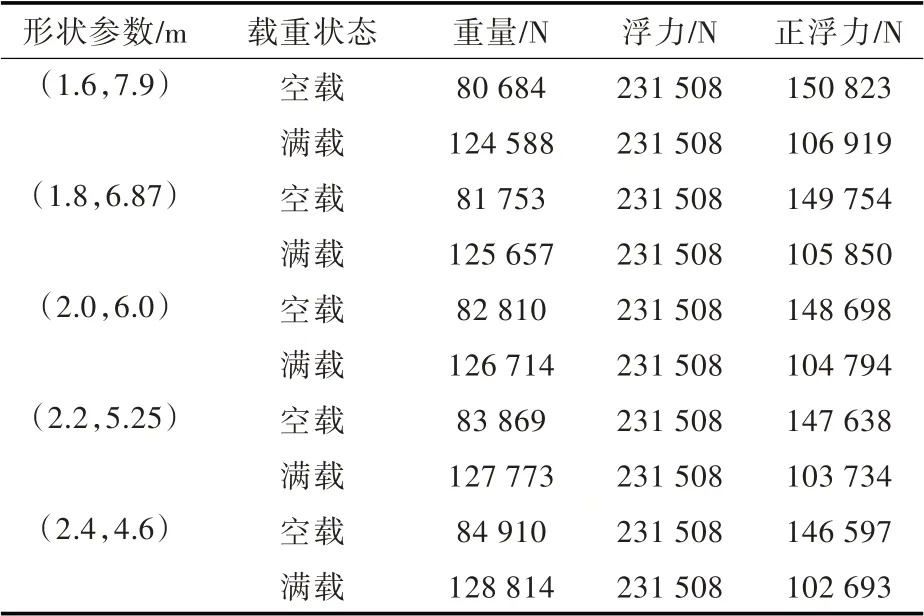
表1 集体逃生舱基本参数表Tab.1 Basic parameters of escape capsule

集体逃生舱上浮运动过程中竖直方向的总阻力可分为摩擦阻力与粘压阻力。逃生舱在自由上浮过程中，当深度足够时，最终将以稳定的速度上浮。在使用FLUENT 软件对模型进行计算时，采用迭代的方法，以不同的速度值作为入口边界条件，计算各速度下潜艇集体逃生舱的阻力，当总阻力值与集体逃生舱的正浮力值（浮力与重力之差）相等时，此时的速度即为逃生舱的最大稳定速度。将上浮运动的计算域定为长方体，模型如图2（a）所示，其中计算域的首部距逃生舱1 倍舱长，尾部距逃生舱3 倍舱长，外边界距逃生舱1 倍舱长。

具体计算条件设置如下：求解器为二维隐式非耦合稳态求解器；湍流模型为RNG k-ε模型；材料为海水，密度1 025.91 kg/m3，粘性0.001 22；边界条件设置为入口速度条件（入口速度为各尺寸集体逃生舱上浮稳定速度经验公式所得数值的附件速度区间）；收敛标准为1×10-6。

使用FLUENT 进行计算所得的结果为各入口速度条件下集体逃生舱的摩擦阻力值与粘压阻力值，当总阻力值与集体逃生舱的正浮力相等，并且和各自的经验公式值接近时，此时所迭代的入口速度值即为逃生舱的稳定上浮速度。

2.2.2 计算结果及验证

采用FLUENT 进行计算，直径递增的各个集体逃生舱其空载和满载状态下对应的最大稳定上浮速度值及阻力值如表2 所示。最大稳定速度下的摩擦阻力值和粘压阻力值一起构成了集体逃生舱竖直方向的总阻力，分别将摩擦阻力和粘压阻力与各自对应的经验公式值进行对比，以此来验证计算结果的正确性。表2 中，以总阻力值代表摩擦阻力和粘压阻力之和，并用总阻力值对比经验公式计算结果，得到仿真计算结果与经验公式计算结果的总体误差。从表2 中可以看出，计算结果与经验公式结果吻合较好。

为了验证自由上浮过程中数值模拟结果的正确性，对逃生舱最大上浮速度下的摩擦阻力值和粘压阻力值的验证分别按照标准ITTC 公式（光滑）和巴甫米尔经验公式［7］进行了对比，对比结果吻合良好。从表2 中可以看出，总阻力值的误差也比较小，证明了数值模拟结果的正确性。

表2 最大稳定上浮速度及对应的阻力值对比表Tab.2 Comparison of the biggest stable floating velocity and resistance

雷诺数：

摩擦阻力系数（标准ITTC 公式）：

摩擦阻力经验公式：

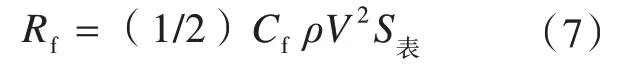
粘压阻力系数（巴甫米尔经验公式）：

粘压阻力经验公式：

以上式中：V 为逃生舱的最大稳定上浮速度；L为逃生舱总长；υ 为动粘性系数；S表为逃生舱湿表面积；ρ 为海水密度；Am为逃生舱中部横剖面面积；Lr为逃生舱后体的长度（流段长度）。

2.3 潜艇集体逃生舱垂直入水运动数值模拟

2.3.1 入水过程仿真模型的建立

潜艇集体逃生舱运动过程的第3 阶段是冲击入水。近年来。随着计算机技术的快速发展，可以采用数值模拟的方法对入水冲击问题进行数值分析［8］。本文采用ANSYS/LS-DYNA 真实再现入水冲击的过程，分析比较各个模型在其出水高度自由下落时水面对模型的最大冲击力。

逃生舱模型采用Lagrange 实体单元，每个舱体载重通过换算成舱体密度进行预载。逃生舱模型的材料泊松比为0.3，弹性模量为210 GPa；逃生舱的实体网格数为7 512 个，单元类型为Solid 体单元。水和空气两种介质采用Euler 网格建模，其网格数分别为：水介质125 000 个，空气介质25 000 个，单元类型选用Solid 体单元。欧拉域空气层尺寸为10 m×10 m×1.5 m，密度为1.2 kg/m3；水层尺寸为10 m×10 m×10 m，密度为1 000 kg/m3。仿真模型如图2（b）所示。

2.3.2 计算条件设置

定义整个分析时间为逃生舱与水面接触开始的30 ms［9］，仿真计算的初始时间步长为2×10-4s，最小时间步长为2×10-4s，在预载的情况下施加重力场9.8 m/s2。通过输出各节点的压强与时间的曲线来反映底部冲击压力的分布情况［10］。

2.3.3 计算结果

对5 个逃生舱模型分别选取相同的节点并输出各节点的压强随时间的分布规律，以此反映压力的变化。由于舱体底部中心处的节点是产生最大冲击力处，因此，将通过对比各舱体底部中心节点的压强分布来分析因尺寸参数及速度的改变对逃生舱最大冲击力的影响规律。

3 计算结果分析

3.1 自由上浮运动数值模拟结果分析

由表2 的结果可以看出，直径递增的集体逃生舱在空载和满载状态下其总阻力会减小，最大稳定上浮速度值则会减小，表明增大集体逃生舱的直径有助于降低最大上浮速度。假设一个最危险的情况，即逃生舱垂直出水，认定出水后最大速度保持不变，经过上升过程和自由落体过程后，各逃生舱仍将以各自的最大上浮速度冲击水面。

3.2 入水冲击运动数值模拟结果分析

在冲击入水的数值模拟中，选取了各个逃生舱模型底部中心的节点，输出节点的压强随时间的变化曲线如图3 和图4 所示。从计算结果中可以看出，逃生舱的最大入水冲击力是依次减小的，表明增加逃生舱的直径可以减小逃生舱的最大入水冲击力。

图3 空载状态下各逃生舱在其初速度下耦合面的冲击载荷峰值时历曲线Fig.3 Time history curves of the coupling surface impact peak with no-load at the initial velocity

图4 满载状态下各逃生舱在其初速度下耦合面的冲击载荷峰值时历曲线Fig.4 Time history curves of the coupling surface impact peak with full-load at the initial velocity

4 结 论

集体逃生舱若体积不变，只增加直径，其重量将会增大，但各自的最大上浮速度却会变小，这对集体逃生舱冲击入水的最大冲击力影响难以估计，也即表明在保证全员救生的前提下，改变集体逃生舱的尺寸参数对逃生舱安全性的影响难以估计。为此，本文采用FLUENT 和ANSYS/LS-DYNA分别对集体逃生舱的自由上浮阶段及入水问题进行了数值模拟，得出不同尺寸潜艇集体逃生舱从自由释放到冲击入水的整个运动过程中，其最大上浮速度及最大冲击载荷。分析了尺寸参数的改变对集体逃生舱安全性的影响，获得了如下结论：

1）体积不变，增加直径，将会减小集体逃生舱的最大出水速度，从而减小冲出水面的高度。

2）体积不变，增加直径，将会减小集体逃生舱的最大入水冲击力，这对集体逃生舱的安全性有利，能够增大艇员的生存几率。

3）本文所建立的计算机仿真模型能够模拟潜艇集体逃生舱的运动过程，也可用于研究各个参数对集体逃生舱运动过程的影响规律，从而为集体逃生舱的设计提供帮助。同时，该仿真模型还有助于集体逃生舱模型试验研究阶段的开展。

［1］张万波，汪新宇，劳健锋.潜艇逃生和营救技术现状与发展［J］. 船海工程，2001（5）：19-24.ZHANG Wanbo，WANG Xinyu，LAO Jianfeng. A re⁃view of submarine escape and rescue［J］. Ship and Ocean Engineering，2001（5）：19-24.

［2］舒斌，胡刚义，肖伟，等. 圆柱体大开孔补强的应力集中分析［J］.中国舰船研究，2011，6（2）：35-39.SHU Bin，HU Gangyi，XIAO Wei，et al. Stress con⁃centration analysis of reinforced cylindrical shells with large opening［J］. Chinese Journal of Ship Research，2011，6（2）：35-39.

［3］黄景泉，张宇文. 鱼雷流体力学［M］. 西安：西北工业大学出版社，1989.

［4］RIIHIJARVI J，MAHONEN P，SAARANEN M J，et al.Providing network connectivity for small appliances：a functionally minimized embedded web server［J］.IEEE Communications Magazine，2001，39（10）：74-79.

［5］陈玮琪，颜开，史淦君，等. 基于TSK 智能技术的物体垂直出水运动参数辨识研究［J］.水动力学研究与进展（A 辑），2005，20（4）：446-451.CHEN Weiqi，YAN Kai，SHI Ganjun，et al. Parame⁃ter identification of hydrodynamic forces of water-exit body based on TSK fuzzy system［J］. Journal of Hydro⁃dynamics（Ser.A），2005，20（4）：446-451.

［6］黄祥兵，黄兴玲，董云飞.潜艇集体逃生舱上浮水动力性能［J］.海军工程大学学报，2013，25（3）：78-81.HUANG Xiangbing，HUANG Xingling，DONG Yun⁃fei. Hydrodynamic performance analysis of surfacing motion of submarine escape capsule［J］. Journal of Na⁃val University of Engineering，2013，25（3）：78-81.

［7］盛振邦，刘应中. 船舶原理（上册）［M］. 上海：上海交通大学出版社，2003.

［8］夏斌，陈震，肖熙.弹性平底海洋结构物入水冲击的仿真分析［J］.中国海洋平台，2005，20（1）：22-28.XIA Bin，CHEN Zhen，XIAO Xi. The simulation anal⁃ysis of the slamming of elastic flat-bottom marine struc⁃ture［J］.China Offshore Platform，2005，20（1）：22-28.

［9］DE BACKER G，VANTORRE M，BEELS C，et al. Ex⁃perimental investigation of water impact on axisymmet⁃ric bodies［J］. Applied Ocean Research，2009，31（3）：143-156.

［10］ARISTOFF J M，BUSH J W M. Water entry of small hydrophobic spheres［J］. Journal of Fluid Mechanics，2009，619：45-78.