解决问题的策略——转化在小学数学总复习中的应用

张迎雪

作为六年级毕业前的总复习，所涉及到的内容是小学所学习到的12册的内容，而总复习时间紧迫这是现实，我们不可能把以前学过的那么多的内容和知识点一一呈现，而且知识相当凌乱。我认为总复习最重要的目标便是在学生的头脑中形成一个系统，几条“绳”，拽出一条“绳”便出来一系列的知识点和内容，让学生对六年所学习的数学知识在头脑中进行系统化的梳理。如果按照以前的复习方式，我们要拿出几节课的时间来分别复习面积知识、体积知识、计算以及分数应用题，而且仅仅是就知识复习知识，学生不能得到应有的提高，这样的复习没有多大的价值。出于这样的考虑，又受到平面图形的面积这一部分的启发，在复习这部分知识时充分运用了转化这种思想，把新知识转化成以前学过的知识，从而解决新的问题。

其实在我们的数学学习中，转化是一种最为常见的策略，不仅仅平面图形的面积中用到，在体积中也涉及到，比如求圆柱圆锥的体积。在计算中比如乘除转化，分数小数转化，可以使计算简便。在分数百分数解决问题中告诉我们一个条件，我们可以转化成不同的理解方式，从而得到不同的解题思路。而且在本节课中，让学生知道有转化这种解题策略不是最重要的，最终目的是提炼出一些具体的转化方法，比如切割、平移、旋转、聚零为整、拆分、以实代虚——不会出现学生看到题目知道要去转化，却不知道怎么转化。

想到这里不禁觉得惊喜，就转化这一种解题策略，居然可以把数学中的平面图形的面积，立体图形的体积，计算以及解决问题这几个领域串联在一起，一起进行复习。可想而知，原来需要用几个课时进行复习的内容放在一个课时，由转化这一条线拉出来，而且还可以对某些题目进行思维的拔高，解决一些扩展题目。

出于这样的考虑，设计本案例如下：

【教学描述】

一、课前引入转化策略

通过爱因斯坦的名言“想象力比知识更重要，因为知识是有限的，想象力却概括着世界上的一切”引入：

联想力作为想象力的一种，在生活中经常用到，比如:

1.看到一个苹果，你会想到什么？

2.告诉你姚明，你会想到什么？

3.由甲是乙的2/3，你会想到什么？

评析：课前通过这样轻松愉快的思维训练，引出本节课的主要思想方法——转化，激起学生的学习兴趣，并对本节课有所期待。

二、复习面积、体积、计算方面的知识

1.出示图形：

（1）仔细观察，哪幅图形的面积大？

学生汇报方法和结论。

（2）在变化过程中使用了哪些具体的操作方法？（切割，平移，旋转）

通过切割、平移、旋转，我们把两个不规则图形变成了长方形，使一个复杂问题变得简单。同学们在不知不觉中就使用了一种非常重要的解决问题的策略——转化。

1.转化在我们以往的数学学习中经常用到，而且用它解决过许多问题，回想一下，哪儿用到过？怎么用的？

（1）面积方面：把平行四边形通过切割平移转化成长方形，把圆转化成近似的长方形，运用了剪拼法。

（2）体积方面：把圆柱转化成长方体。

（3）计算方面：分数除法转化成分数乘法；异分母分数加减法转化成同分母分数加减法；小数乘法先按整数乘法计算，再确定小数点。

解决这些题目的共同点都是把当时未知转化成已知，只是具体的转化方法不尽相同。

评析：从使用转化最为突出的平面图形的面积入手，具体复习怎么运用转化得到不同的平面图形面积的计算方法，对具体的操作方法和计算公式进行复习。并利用小组合作学习的方式回忆在整个数学学习中哪里还用到过，从而对体积方面的计算公式和计算方面的计算法则进行了复习。

三、练习中提炼出具体的转化方法，体会转化的策略

1.用分数表示涂色部分：

图中涂色部分分别占整个图形的几分之几？

第三副图，学生遇到困难。学生可自由讨论，得到方法把三角形旋转180度，得1/4。

2.怎样知道涂色部分面积的和是多少？

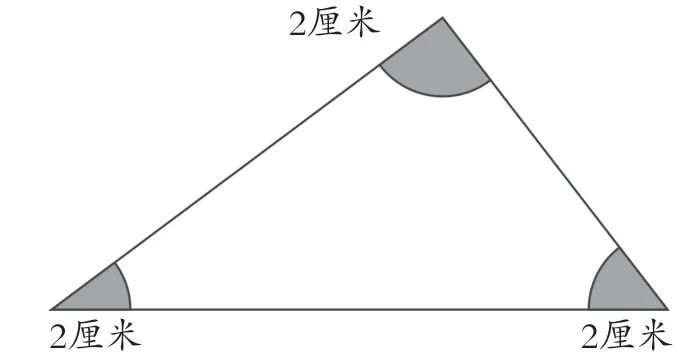
三角形内角和是180度，扇形半径相等，所以涂色部分可以拼成一个半圆。课件演示，要求涂色部分面积和就可以转化成求半圆的面积。

解决这样分散的问题可以转化成一个整体，这种方法叫什么呢？（聚零为整）

这个可以么？具备聚零为整的条件么？

四边形内角和为360度，扇形半径相等，可以拼成一个圆，求圆的面积就可以。

3.在计算中也常常将数据转化来解决问题。

（1）19.99÷5/2-0.4×9.99。小结：把除法转化成乘法，出现了相同的数，可以使用乘法分配律。

（2）22×43+19×66，这个能不能也转化出相同的数呢？

学生出现不同的方法：11×2×43+19×6×11，22×43+19×3×22。比较两种方法，显然第2种比较简单，提出转化需要技巧。

（3）1/2+1/4+1/8+1/16+1/32+1/64+……+1/1024，这么复杂的问题怎么解决？

提议：先解决简单的：1/2+1/4+1/8+1/16，如果能从中发现规律，就可以运用规律来解决复杂的问题。学生自己想办法解决。

汇报：1/2+1/4=3/4，1/2+1/4+1/8=7/8，1/2+1/4+1/8+1/16=15/16。

拆分法：1-1/2+1/2-1/4+1/4-1/8+1/8-1/16。

画线段图解决（数形结合）。

课件演示：

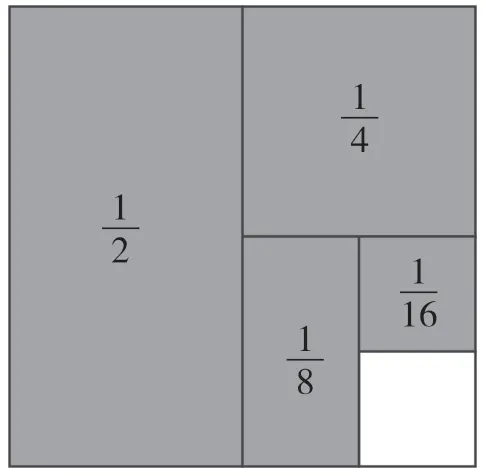
转化成1-1/16。

如果再加到1/32，想想该怎么继续往下画，怎么求？1-1/32。

再加多少？1/64，怎么求？

能解决1/2+1/4+1/8+1/16+1/32+1/64+…+1/1024=？

评析：转化在计算中的应用，除了基础的，多数体现在简便计算中，上边的几个计算题，层层提高。对于部分学生来说也许开始没有思路，但听到别人的解答方法便很容易理解，在这转化起了很大的作用。

4.转化技巧也常常运用到应用题的分析推算中。

（1）等底等高的圆柱和圆锥，它们的体积之差是8立方厘米，圆柱和圆锥的体积分别是多少？

汇报：3x-x=8

x-1/3x=8

8÷(1-1/3)

8÷(3-1)

（2）有两枝蜡烛，当第一支燃去4/5,第二枝燃去2/3时，它们剩下的部分一样长，这两枝蜡烛原来长度的比是多少？

学生合作完成：一×1/5=二×1/3

都等于1，则一是5，二是3，一：二=5：3

方法：以实代虚，把等积式转化成比例式。

评析：让学生单独去想转化在哪里用到过，学生很难想到在解决问题中也有，所以在前边的小组学习中，学生不会提出来。因此，这里由老师出示题目让学生看到，原来我们在解决这些问题的时候，很自然地也使用了转化这种方法，不仅可以解决问题还可以多种方法来解决。

5.拓展

求涂色部分的面积。

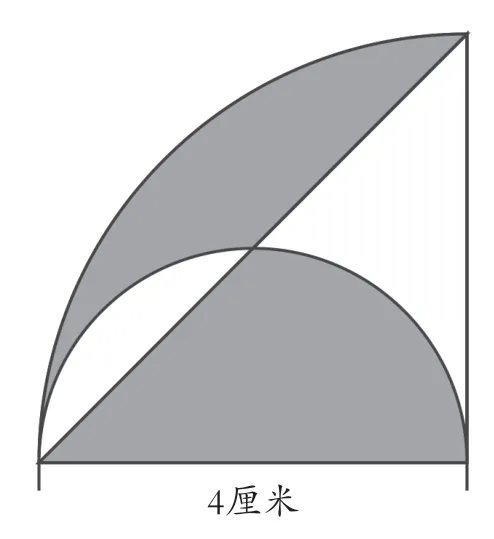
【教学反思】

1.教学生一种思想方法胜于知识本身，这将是学生一生的财富。我认为这是一节思想方法课，所以着重于学生思想的渗透和方法的训练。这节课中涉及到的面积、计算和解决问题等各个领域，在我们课本中处于零散知识，根据转化这个方法把这些内容贯穿在一起，使学生在头脑中有了明晰的认识，可以运用转化来解决这样的问题。作为这些知识系统的复习，要让学生自己自主地去复习，所以在课上并不需要老师花费太多的时间去具体讲解，只要让学生把方法提炼出来就可以。本节课以转化作为一个思想，以各种具体的方法作为操作手段，尽量做到一题一得。目的在于让学生知道遇到问题我可以去转化，但是具体怎么转化，让学生得到一些摸得着的方法，可以去试试移移、转转还是怎么样。其实不光学习是如此，人们在生活、工作中也会遇到许多的问题，同样可以运用转化这种策略来予以解决。

2.要想让学生爱上数学，我们的设计就要激发起学生的兴趣，让他们有要去征服的欲望。我感觉对于本节课，首先是激起了学生的学习兴趣。课上的好多问题都是学习比较困难的学生来回答的，他们都敢于去思考发言，我想这是他们对于内容是感兴趣的。练习层次分明，对于大部分题来说我觉得不是特别困难，是大部分学生可以伸伸手就能够到的。个别题目也许是有些拔高，部分学生可能没有思路，但听到其他学生的汇报他们也能明白为什么这样做，对他们来说也是收获。再就是既然以方法贯穿始终，那比如最后一个拓展题，也许没上这节课之前他们遇到会无从下手，但学习了这些方法以后，他们就会想着要去转化，去移，去补，可能只是一个小小的进步，但也能有所得。在本节课中不仅仅让学生知道了转化这种解题策略，而且还知道了许多具体的转化方法，比如切割、平移、旋转、聚零为整、拆分、以实代虚等。

3.典型题目牵引出的具体方法。选择练习题目，真的需要精选。关于转化的这些题目，我们也是再三地取舍、更改，选择有代表性的、有价值的真的并不是太容易。但我们复习时间有限，要想效率高，那就需要精讲精炼，所以选择练习题特别是复习阶段的练习题需要我们多动脑筋。我感觉在我们学习数学的整个阶段，转化这种方法是贯穿始终的。它的主旨不就是化繁为简、化新为旧么？我们遇到的数学问题不都要这样解决么？所以对于一些解决问题的策略，什么转化、代换……我感觉都是相通的，没有什么明显的界限。