求函数极限的方法

赵士元

（朔州师范高等专科学校，山西朔州，036002）

求函数极限的方法

赵士元

（朔州师范高等专科学校，山西朔州，036002）

用极限方法研究函数是高等数学乃至分析系统各门课的显著特征。本文对求函数极限的方法加以归纳、总结，以帮助初学者更深刻地理解极限的概念并熟练掌握求极限的方法。

函数极限；洛必达法则；两边夹定理；等价代换

函数极限是高等数学中最抽象的概念，是高等数学的难点和重点，高等数学中的许多概念和定理都与极限有关。从连续到导数、从微积分到级数等都是用极限来定义的，极限贯穿了高等数学的始终。因此，全面掌握函数极限与求极限的方法及技巧是学好高等数学的基本要求。

一、利用定义证明函数极限的存在

二、求多项式函数的极限的方法

三、利用重要极限求函数极限

四、利用极限的四则运算法则求极限

五、利用两边夹定理求极限

六、利用无穷小的性质求极限

无穷小量的性质

（1）若函数f（x）与g（x）（x→a）都是无穷小，则函数f（x）±g（x）（x→a）与f（x）g（x）（x→a）也都是无穷小。

（2）若函数f（x）（x→a）是无穷小，函数g（x）在a的去心邻域U˚（a）有界，则函数f（x）g（x）（x→a）也是无穷小。

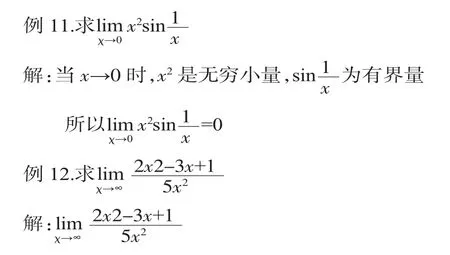
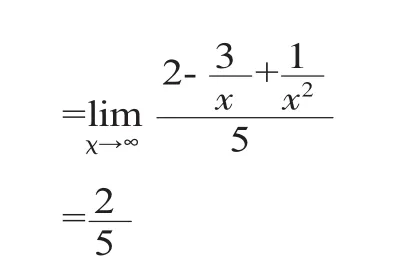
七、利用洛必达法则求极限

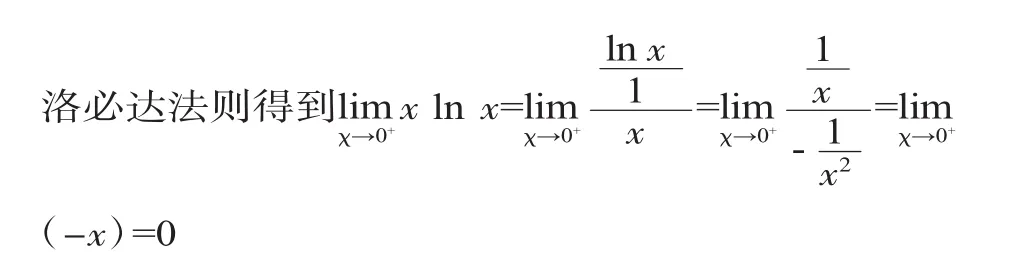
八、利用等价代换求极限

在求乘除式极限时，其因子可以用等价因子代替，极限值不变，最常用的等价代换有arcsinx▯x，arctanx▯x，ln(1+x)▯x，ex-1▯x，ax-1▯xln a，1-cosx

在很多情况下，我们可以把题目中的无穷小量用恰当的等价无穷小量来替换，从而化繁为简，化难为易，但在等价无穷小量的替换时应注意，可以对不定式中相乘或相除的因式进行替换，但对极限中相加或相减部分不能随意替换。

九、利用导数定义计算函数极限

十、利用中值定理求函数极限

对于一些含有积分式子或分式的极限，可考虑利用积分中值定理或微分中值定理进行求解

十一、利用泰勒公式求函数极限

当极限式中含有复合函数，且用前几种方法求极限较为困难时，考虑用泰勒公式（或马克劳林公式）求极限

十二、利用左右极限求分段函数在分界点处的极限

本文针对学习函数极限计算的同学遇到的问题，给出了函数极限计算的方法与技巧，并结合例题对一些数学名词和理论作了解释，然而，任何方法都不是万能的，步骤也不是一成不变的，如何将求函数极限的这些特殊方法融入到更多的函数极限计算的题型中，是一个值得研究的问题。

[1]刘玉琏．数学分析讲义[M】．北京：高等教育出版社，1997．

[2]同济大学数学教研室．高等数学(第四版)[M】．北京：高等教育出版社，l996．

[3]费定晖，周学圣．数学分析习题集题解[M1．山东：山东科学技术出版社，2009（5）．

[4]同济大学数学系．高等数学(上册)[M]．北京：高等教育出版社，2007（4）．

[5]华东师人教学系．数学分析(第l版)【M】．北京：高教出版社，199l，3．

[6]B．Ⅱ吉米多维奇．数学分析习题集【M】．济南：科学技术出版社，2005（1）．

编辑 朱荣华

O13

A

2095-8528（2014）03-007-02

2014-10-09

赵士元（1985-），男，山西朔州人，在职研究生，朔州师范高等专科学校数计系助教，研究方向向数学与应用数学