浅谈抽象矩阵的秩
2014-02-03张仙凤
张仙凤
(朔州师范高等专科学校,山西朔州,036002)
浅谈抽象矩阵的秩
张仙凤
(朔州师范高等专科学校,山西朔州,036002)
矩阵的秩是矩阵最重要的特征之一,在线性代数研究中有着很重要的作用。对于矩阵秩的问题,大家探讨的也比较多,而本文是从抽象矩阵来探讨矩阵的秩的。抽象矩阵的秩是矩阵求秩的难点之一,本文则对抽象矩阵从等式与不等式两个方面来探讨求秩。
秩;抽象矩阵;列向量;单位矩阵;分块矩阵
抽象矩阵是矩阵的一种特殊形式,即不给出矩阵的元,而只是告诉矩阵具有某些性质。抽象矩阵求秩的问题,由于所给矩阵性质多样,决定了我们在遇到相关问题时,解题的思路和方法不是单一的,而是多种多样的。我们应该根据题目所给出的性质,应用矩阵相关的定义及定理灵活的去求解。
一、矩阵的秩的相关定义及定理
1.矩阵的秩的两种定义:
定义1:矩阵行秩等于矩阵列秩,统称为矩阵的秩。
定义2:矩阵中非零子式的最高阶数叫做矩阵的秩。
矩阵M的秩记为:秩(M)
2.矩阵的秩的相关定理:
定理1:M、N分别为m×n,n×s矩阵,则秩(MN)≤min{秩(M),秩(N)}。
定理2:秩(M)-秩(N)≤秩(M±N)≤秩(M)+秩(N)。
定理3:M、N为n级方阵,如果MN=E,则M、N都是可逆矩阵,且他们互为逆矩阵。
定理4:是一个m×n矩阵,如果P是m×m可逆矩阵,Q是n×n可逆矩阵,则秩(PM)=秩(MQ)=秩(M)。
定理五:对于分块矩阵秩

二、抽象矩阵的等式类型
命题1.设M是n阶方阵,秩(M)=p,Nk=0,求证(MN-M)=p

因为MN-M=M(N-E)
所以秩(MN-M)=秩(M)=p
(方法二)Nk=0,则E=E-Nk=(E-N)(E+N+N2+..... +Nk-1
所以E-N可逆
所以秩(MN-M)=秩(M)=p
总结:该题的难点是要得出条件中Nk=0的有关结论,这是个高次形式,而且是一般性的k次形式,那我们推出的结论也是具有一般性的,即Nk=0,则有NE为可逆矩阵。
命题2.设n阶矩阵M,N,P,Q关于矩阵乘法可以交换,如果,MP-NQ=E,E是n阶单位矩阵。求证:秩(MN)=秩(M)+秩(N)-n

总结:该题构造分块矩阵,利用分块矩阵的秩的相关定理去求解。
命题3.设M为m×n矩阵,证明:秩(Em-MM′)-秩(En-M′M)=m-n

由于初等变换不改变秩,所以秩(Em-MM′)-秩(En-M′M)=m-n
总结:要善于观察,构造分块矩阵是难点。
命题4.若M为实矩阵,则秩(M′M)=秩(M)=秩(M′)=秩(MM′)
证明:设M是s×n实矩阵,则M′M是n×n实对称矩阵
考虑齐次线性方程组M′MX=0与MX=0
显然MX=0⇒M′MX=0
相反,M′MX=0⇒(MX)′(MX)=X′M′MX=0
因为,MX是实s维列向量,(MX)′(MX)=(MX,MX)是MX的内积
所以,0=(MX)′(MX)=(MX,MX)⇒MX=0
可知:M′MX=0⇒MX=0,即齐次线性方程组M′MX=0与MX=0同解
秩(M′M)=秩(M)=秩(MM′)
总结:该题是从方程组解的角度去求解的,将求秩的问题转化为方程组同解。
命题5.M是n阶方阵,则秩(Mn)=秩(Mn+1)=秩(Mn+2)=…
证明:证明题目成立,即证MnX=0,Mn+1X=0,Mn+2X=0,…同解
若Mn=0,则Mn+1=0(X是n元列向量),即MnX=0的解都是Mn+1X=0的解,
若Mn+1X=0,则MnX=0.否则MnX≠0,有n+1个向量X,MX,...,Mn-1X,MnX线性无关,因为若k0X+ k1MX+...+knMnX=0依次用Mn,Mn-1,...用乘该式得到,k0=k1=...=k1=kn=0,这与X是n元列向量矛盾。可知MnX=0可知Mn+1X=0的解都是MnX=0的解.所以方程组MnX=0,Mn+1X=0同解.可知秩(Mn)=秩(Mn+1),同理可得秩(Mn)=秩(Mn+1)=秩(Mn+2)=…
总结:该题是扩展了矩阵的次幂形式。
三、抽象矩阵的不等式类型
命题1.设M、N为n阶矩阵,E为n阶单位矩阵,矩阵M-E及N-E的秩分别为s和t,则矩阵秩(MNE)≤s+t

总结:定理2是关于两矩阵秩的和、差的关系,定理4是关于两矩阵秩的乘积的关系,在遇到矩阵秩的不等关系证明时考虑用这两个定理。
命题2.若M、N分别为m×n和n×t矩阵,则秩(MN)≥秩(M)+秩(N)-n
证明:设E为n阶单位矩阵
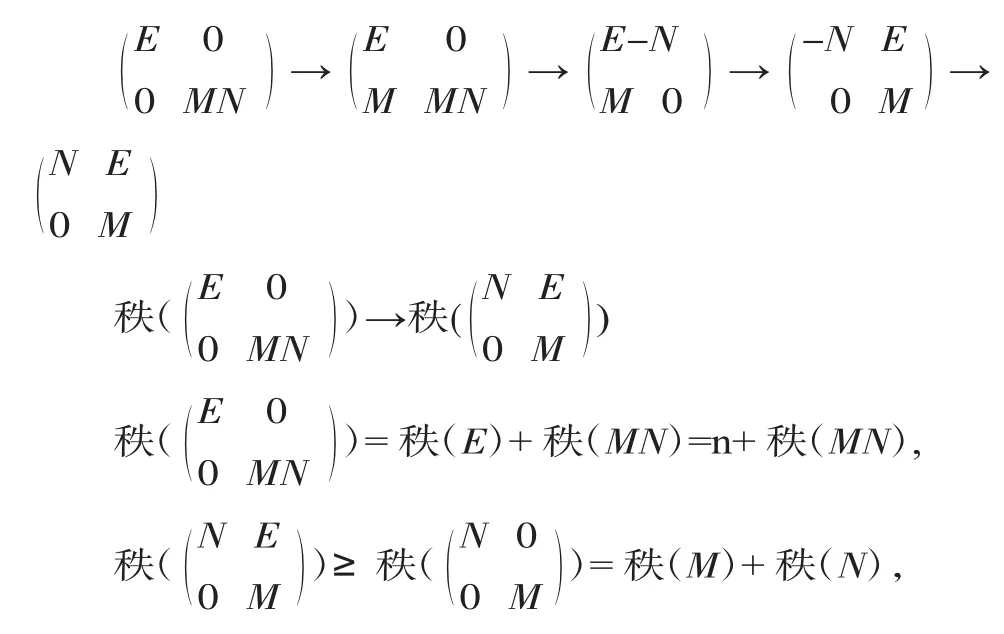
秩(MN)≥秩(M)+秩(N)-n
总结:构造分块矩阵来证明,要灵活应用定义及相关定理。
命题3.M、N、P为n阶矩阵,求证:秩(MNP)≥秩(MN)+秩(NP)-秩(N)

所以秩(MNP)≥秩(MN)+秩(NP)-秩(N)
总结:该题将两个矩阵乘积扩展为三个矩阵的乘积
命题4.M是一个方阵,求证:秩(M3)+秩(M)≥2秩(M2)
证明:由上个命题可知秩(M3)=秩(MMM)≥秩(M2)+秩(M2)-秩(M)
可知秩(M3)+秩(M)≥2秩(M2)
总结:该题利用命题三的结论,将三个连乘变为矩阵的次幂形式。
命题5.M1,M2,...,Ms均为n阶方阵,M1,M2,...,Ms=0
求证:秩(M1)+秩(M2)+…+秩(Ms)≤(s-1)n
证明:由命题2可知:
秩(M1,M2...Ms)≥秩(M1)+秩(M2,M3,...,Ms)-n≥
秩(M1)+秩(M2)+秩(M3,...,Ms)-2n≥
秩(M1)+秩(M2)+…+秩(Ms)-(s-1)n
又M1M2...Ms=0,秩(M1M2...,Ms)=0
所以秩(M1)+秩(M2)+…+秩(Ms)-(s-1)n≤0
即秩(M1)+秩(M2)+…+秩(Ms)≤(s-1)n
总结:该题是把矩阵扩展到s次幂的形式,更具有一般性。
矩阵的秩是矩阵的一个重要属性,是研究矩阵的核心,而抽象矩阵的秩是重点中的难点。我们有必要把分散的知识点及一些题型整合在一起,便于我们总结和掌握。以上命题的类型和解题思路在一般的抽象矩阵求秩问题中都是适用的,有其普遍性,值得借鉴和推广。
[1]北京大学数学系.高等代数[M].北京:高等教育出版社,2003.
[2]钱吉林.高等代数题解精粹[M].北京:中央民族大学出版社,2009
[3]国慧.矩阵的秩及应用[J].邢台学院学报,2011(2).
[4]王萼芳.高等代数题解精粹[M].北京:高等教育出版社,2002.
[5]孙敏.高等代数方法研究[M].昆明:云南大学出版社,2009.
[6]邱森,朱林生等.高等代数探究性课题集[M].武汉:武汉大学出版社,2008(8).
编辑 朱荣华
O13
A
2095-8528(2014)03-118-03
2014-10-17
张仙凤(1982~),女,山西朔州人,本科,朔州师范高等专科学校数学与计算科学系助理讲师,研究方向为基础数学。
