以固有特性为目标函数的振动筛结构形状优化设计
2014-02-02安晓卫徐文彬李秀艳李素妍
安晓卫,穆 珊,徐文彬,李秀艳,李素妍
(1.沈阳理工大学 机械工程学院,辽宁 沈阳 110159;2.鞍山重型矿山机械股份有限公司,辽宁 鞍山 114051)
振动筛是筛分机械中的重要设备,大处理量、高效率是其发展趋势。振动筛在恶劣的工作条件下常常由于激励引起的共振使侧板断裂、筛框扭曲变形等故障,对振动筛的结构布局进行优化设计,提高其结构刚度,不仅能延长振动筛的使用寿命,还可以带来巨大的经济效益。
文献[1]用Solidworks软件建立筛体的三维实体模型,对圆振动筛进行模态分析,得到筛箱的固有频率和振型;文献[2]对大型直线振动筛进行了动态仿真和仿真测试,并根据计算结果对大型筛体做了改进设计;文献[3]以ZK450直线振动筛为研究对象,运用有限元分析软件ANSYS进行动态特性分析,计算出固有频率和模态振型及在额定载荷下的应力分布情况,为以后振动筛的设计提供了参考和借鉴;文献[4]对振动筛在ANSYS中进行强度仿真,得到振动筛的强度规律,从试验结果出发,对振动筛进行寿命估计;文献[5]嵌入解析灵敏度法将板厚和截面宽度作为设计变量,以减小侧板质量为目的,对振动筛进行优化设计;文献[6]以筛箱各板厚为设计变量,以总质量为目标函数对筛箱结构进行优化计算;文献[7]对大型圆振动筛进行动力学分析和动态优化设计。但是文献[5-7]只将某些板厚作为设计变量对振动筛进行优化,并没有考虑各构件位置布局对其固有特性的影响;文献[8]中为使固有频率远离激励频率,在筛框底部增加了两条纵向矩形加强梁以提高整体结构的纵向刚度。文献[1-8]对振动筛的修改只是凭设计者的经验,缺少一定的理论依据;结构优化设计大多停留在尺寸优化层次上,对于振动筛这样大型复杂的工程机械进行整机优化并涉及灵敏度这方面的研究资料尚少[9]。而关于振动筛结构形状优化方面的研究几乎是空白。
振动筛结构复杂,影响结构动态特性的因素多。为避免结构修改的盲目性,提高优化设计的计算效率,减少计算成本,本文通过灵敏度分析,寻找出结构的薄弱环节,以对结构特性影响大的参数作为设计变量,对某振动筛的结构布局进行形状优化设计。
1 振动筛模型处理及模态分析
1.1 有限元模型处理
振动筛的外形尺寸长、宽、高分别为9.117m、4.9m和3.49m。其结构主要是侧板、上下横梁、主梁、前后弹簧座耳、U型加强板、后挡板和支撑角钢等组成,其材料为Q235,侧板是一块整钢板,上、下横梁、主梁、U型加强板和后挡板是由钢板焊接而成,弹簧座耳采用铆焊结构,用两块端板与侧板铆钉连接到一起。振动筛体积大,连接件多,结构复杂。振动筛结构上有一些工艺小孔,由于其仅对很小的局部区域的刚度有影响,对整个振动筛的计算精度影响很小,因此,综合考虑其结构形状、承载方式、边界条件、计算成本与可行性,在满足工程精度的前提下,建模时将这些小孔忽略不计。采用板单元模拟侧板、上下横梁、主梁等结构件;侧板与横梁、主梁等各结构件之间的连接铆钉,采用考虑剪切变形影响的Timoshenko梁单元模拟;筛箱与地面之间的连接金属螺旋弹簧用弹簧单元模拟。离散化后,共生成251997个节点及158532个单元。有限元模型如图1所示。
1.2 模态分析
选取Block Lanczos法对振动筛进行模态分析,计算得振动筛的第一阶固有频率为36.108Hz,其第一阶振型如图2所示。

图1 振动筛有限元模型

图2 第一阶振型图
由图2可见第一阶振型主要是侧板发生的变形,是局部振动。振动筛工作时,侧板是结构主要承载件,分布着很大的惯性力,是易损坏部件。因此,提高振动筛的固有频率,使其固有频率远离激励频率,可减小侧板的动应力,延长其使用寿命。
2 灵敏度分析
在结构设计中,常常需要对结构某些部位做出适当修改,以提高结构的动态特性。对于振动筛这样复杂结构,影响其刚度和强度的因素有很多,并且整机优化的计算量非常大。如果仅凭设计人员的设计经验进行优化设计,由于缺乏理论依据,自然避免不了盲目性,也不能做到以最小的改动达到最佳的效果。
为解决这一问题,对振动筛进行灵敏度分析,确定敏感变量,即找出对系统第一阶固有频率影响最大的因素作为设计变量,提高整机优化的效率。
2.1 基本原理
灵敏度研究动态特性对结构参数的敏感程度,即系统目标函数对设计变量的偏微分。
系统无阻尼自由振动微分方程为

(1)
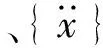
[K]{u}=ω2[M]{u}
(2)
式中,ω为固有频率,{μ}为固有振型向量。
根据式(2)对设计变量xi求偏导,得
(3)
将式(3)左乘{μ}T,由于[K]为对称矩阵,整理得
(4)
由方程(2)[K]{u}=ω2[M]{u},可将式(4)简化为
(5)
将振型向量对质量矩阵做归一正则化处理,并简化式(5),且ω=2πf,得到系统的固有频率对设计变量的灵敏度关系式为
(6)
公式(6)反映了系统固有频率f随设计参数变化的关系。灵敏度值为正数时,说明增加相应变量的值会提高第一阶固有频率,反之则应减小变量值来提高频率。灵敏度的绝对值越大,对结构的影响就越显著。
2.2 设计变量的选择
对振动筛这类复杂结构,修改方案有很多种,可供调整的结构参数也有很多,为确定何种方案最为有效,需分析结构参数或设计变量对结构特性的敏感程度。
振型幅值较大的区域的变动对该阶固有频率的影响较明显;若某部分结构处于振型节点附近,则这部分变动不会对该阶频率有明显的影响[10]。振动筛第一阶的变形主要是侧板的局部变形,为降低优化问题的难度,减少设计变量个数的同时确定有效的设计变量,尽量多选取侧板上变形区域附近的变量进行灵敏度分析。根据上述原则,选取如图3所示与侧板相关的12个变量进行模态灵敏度分析。
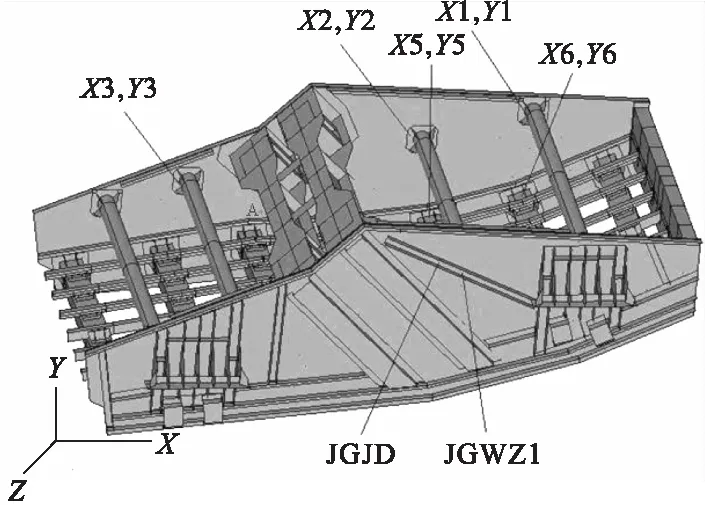
图3 变量名及含义
注:X1、Y1—上横梁1的X和Y方向的位置改变量;X2、Y2—上横梁2的X和Y方向的位置改变量;X3、Y3—上横梁3的X和Y方向的位置改变量;X5、Y5—下横梁5的X和Y方向的位置改变量;X6、Y6—下横梁6的X和Y方向的位置改变量;JGWZ1—斜角钢12在Y方向的位置改变量;JGJD—斜角钢12绕顶点A沿逆时针方向的角度变化。
根据公式(6),编写出相应的振动筛灵敏度计算程序。经过计算,得到各变量对第一阶固有频率的灵敏度,如图4所示。

图4 一阶灵敏度的柱形图
由图4可以看出,X1、X2、Y1、Y2、JGWZ1、JGJD这6个变量的灵敏度数值较大,说明在变形区域这些零件的位置变化对第一阶固有频率敏感;而变量X3、Y3、X5、Y5、X6、Y6灵敏度值较小,说明其改变对结构第一阶固有频率影响非常小。变量JGJD的值为负,说明当JGJD减小时,频率会有所增加。是在确保部件之间不相互干涉的条件下,变量JGJD可取的变化范围非常小,所以当JGJD改变时,很容易与两侧的U型加强板及弹簧座耳干涉;并且变量JGJD对第一阶固有频率的贡献并不非常明显,故在优化时没有把变量JGJD列为设计变量。变量X2的灵敏度值相对于其他五个变量的灵敏度值小,但X2、Y2是影响上横梁位置的一对变量,由于结构装配工艺要求,Y2位置改变时,X2也必需随之改变。
由灵敏度的计算,综合考虑各个变量对结构的影响程度,选择X1、Y1、Y2、JGWZ1这4个变量进行优化设计。计算得到的灵敏度系数均为正值,说明这些变量值增加时振动筛的第一阶固有频率也随之提高,这样确定了设计变量的变化趋势,缩小了设计变量的取值范围。
3 振动筛的优化设计
根据结构装配工艺要求,位于侧板内外侧的斜角钢12和上横梁2是用同一组铆钉相连接,二者位置始终相互对应。结构上要求铆钉不能随其中某一部件位置的改变而移动,所以他们必须是同时变动。故优化设计时将变量JGWZ1和Y2作为一个设计变量,即令Y2=JGWZ1。同样设计变量X2与Y2也存在相应的几何约束关系。因为斜角钢与水平(x轴)的夹角为33.5度,故X2与Y2之间的比例关系为tan33.5=Y2/X2,所以X2=Y2/tan33.5≈1.5×Y2。因此用设计变量Y2代替JGWZ1和X2,则设计变量由5个变成3个:X1、Y1和Y2。这样处理,不仅避免了由于设计变量过多而收敛到局部最优点的危险,同时也可提高计算效率。
在保证结构件之间不相互干涉的条件下,确定设计变量的变化范围。各变量的上限值均为各部件之间不发生干涉情况下的最大变动量。振动筛优化的数学模型为
Minf(X)=min(-freq_1)
61-Y2≥0
47-X1≥0
s.t. 42-Y1≥0
Y2≥0
X1≥0
Y1≥0
设计变量和目标函数freq_1的迭代曲线分别如图5和图6所示。根据计算结果并通过数据圆整,得到各设计变量值分别为X1=42mm,Y1=36mm,Y2=59mm,则JGWZ1=Y2=59mm,X2=1.5×JGWZ1=1.5×59=88.5mm。各部件的位置改变在图7中标出。
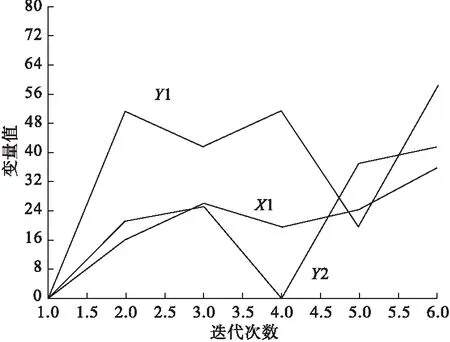
图5 X1、Y1、Y2迭代曲线
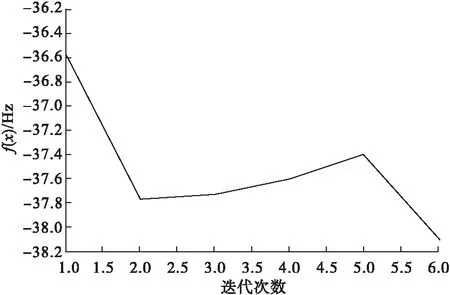
图6 目标函数f(X)迭代曲线
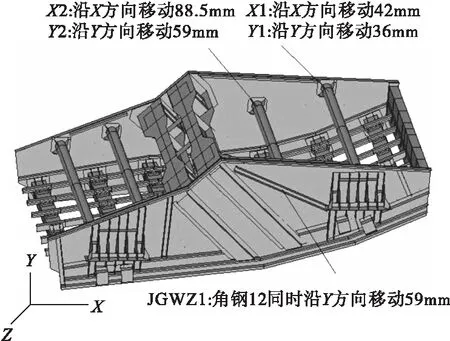
图7 优化后的振动筛模型

图8 优化后的振动筛第一阶振型图
按照优化结果修改结构,再对振动筛进行模态分析,其优化后的固有频率列于表1,对应的第一阶振型如图8所示。
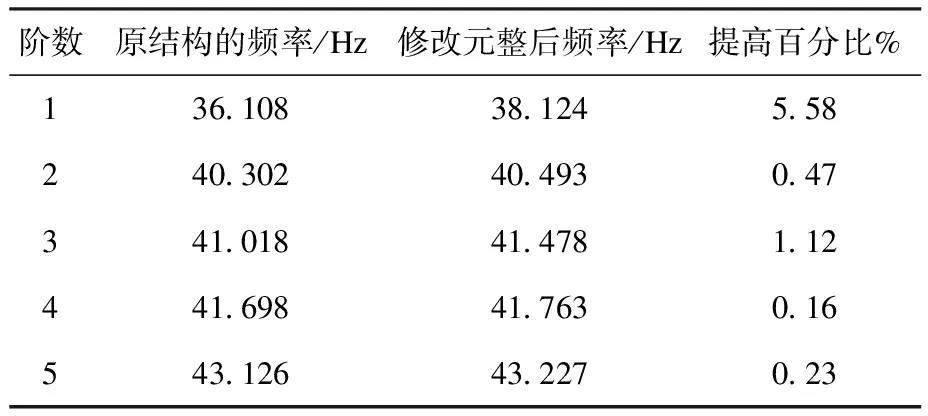
表1 修改前后固有频率
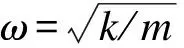
通过对结构进行灵敏度分析可以找出最佳的修正位置,在此基础上进行结构优化设计,可提高优化效率。结果表明,在灵敏度较大部位进行结构修改的方法是行之有效的。
4 动力学分析
对振动筛优化设计后,需进行动力学分析,确定所受的应力以及位移是否满足工作要求。
振动筛所受的简谐激振力在水平方向与铅垂方向的分力分别为349865 sin(ωt)N和-349865 sin(ωt)N,对优化后的振动筛进行动力学分析后,得到振动筛关键部件的应力以及位移,如表2所示。
由表2可以看出,下横梁所受的应力最大,为40.093MPa。图9为下横梁应力随时间变化曲线,由图9可以看出,最大应力出现在t=0.00165s时,此时对应的应力云图如图10所示。

图9 下横梁随时间t变化曲线

图10 t=0.00165s时下横梁应力云图

5 结论
建立香蕉型直线振动筛的有限元模型,对其进行模态分析,得到固有频率以及相应的振型。通过灵敏度分析筛选出对第一阶固有频率影响较大的因素作为设计变量,进行优化设计,避免了优化设计的盲目性,提高计算效率。优化圆整后,第一阶固有频率提高了5.58%。对优化之后的振动筛进行强度校核,验证其满足强度要求。
[1] 杨献辉,赵俊利,薛雷泽.基于ANSYS的SDLl645-1圆周振动筛模态特性分析[J].煤矿机械,2010,31(6):74-76.
[2] 王永岩,邰英楼,孙奇涵.大型直线振动筛动态仿真的研究[J].计算力学学报,2001,18(1):94-98.
[3] 吴炳胜,苏茹茹,李文选.基于ANSYS的ZK450振动筛动态特性的分析[J].煤矿机械,2012,33(2):97-99.
[4] 孟彩茹,李磊,冯忠绪.振动筛的强度分析和寿命估算[J].机械设计,2012,29(7):20-24.
[5] 贺孝梅,刘初升,张成勇.基于多频约束和解析灵敏度法的大型振动筛优化设计[J].中南大学学报,2011,42(3):664-670.
[6] 方治华,赵爽.HFZS1640型振动筛强度的优化设计[J].煤矿机械,2007,28(11):23-24.
[7] 乔崇全,王克杰.大型振动筛动力学分析及动态优化设计[J].煤矿机械,2011,32(11):3-5.
[8] 周磊,刘建慧.振动筛侧板及筛框动态设计[J].机械设计与研究,2010,26(4):108-110.
[9] 赵海军,邓兆祥,胡玉梅.基于灵敏度分析的微型货车车身结构动力修改[J].汽车工程,2008,30(6):534-538.
[10]张军挪,王瑞林,李永建.基于灵敏度分析的机枪结构动力修改研究[J].中北大学学报,2007,28(2):112-116.
[11]成大先.机械设计手册[M].(第一卷).北京:化学工业出版社,2008:107-109.
