可变负载无标度网络鲁棒性分析

徐 野，李 青

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

相继故障[1]是与网络上的传播行为有很多相似之处的一种现象，普遍发生在各种关键生命线系统网络中，如供水网、供气网、交通网、Internet、通信网等。这些网络有一个共同点：存在大量的负载，并且负载都是动态变化的，而且节点承受负载的能力是有限的。相继故障[2]是指复杂网络中的一些节点或者边由于负责过大崩溃后，会通过节点或者边之间的耦合(连接)关系，造成“流”在节点或者边上重新分布，进而引发其他节点或者边发生故障，产生连锁反应，最终导致相当一部分节点甚至整个网络的崩溃。因此，节点或者边的崩溃会在整个网络上传播开，造成对网络的严重破坏。

复杂网络研究无论在理论上还是实际应用中都有着重要的意义。从理论上讲，复杂网络具有三个主要特征：小世界效应、无标度特性和高集聚性[3]。无标度网络具有较小的最短路径且分布呈幂率分布。已有研究结果表明，小的最短路径能够使系统低层次的因素之间的局部交互作用更加密集频繁，从而在系统层次上会涌现出更多的性质。这对于网络的同步行为和疾病传播行为都有显著的影响，而无标度网络的异构性使得疾病传播几乎没有阈值，因此控制流行病就不仅仅是提高医疗水平的问题，而是如何切断网络中的关键连接的问题。从应用上讲，Internet上发生数据拥塞、交通网络中的堵塞等不仅与设计的控制管理协议有关，与整个网络的布局也密切相关。

1999年10月，美国圣母大学物理系的Barabasi教授及其博士生Albert在“Science”杂志上发表了一篇题为《随机网络中标度的涌现》的论文，这篇论文揭示了复杂网络的无标度特性，建立了无标度模型[4]。Barabasi和Albert指出了现实中的网络有两个方面在以前的网络模型中未包含进去。首先，没有考虑现实网络的增长性，相对而言，大部分现实网络是开放的，即他们是由不断加进系统中的新节点组成，因此节点数目N的增长伴随网络的终生。其次，没有考虑网络的优先连接，大部分现实网络展现出择优连接的性质。

本文基于BA无标度网络模型，通过对BA无标度网络的节点引入相关性描述，通过模拟，得到BA无标度网络在受到攻击时的鲁棒性性能变化。通过仿真发现，提高网络鲁棒性的方法不需要对网络中的所有节点进行，而只需对其中最为关键的几个中心节点进行改善可以得到满意的效果。

1 BA无标度模型

1999年，Barabasi和Albert[4]在Science上发表文章指出，许多现实世界的复杂网络并非是规则网络和随机网络，而是属于无标度(scale-free)网络，并对这样一类网络的特征量进行了一些研究，指出了决定互联网、万维网和科学家合作研究网络等具有无标度特性的两个基本性质：节点增长与优先连接。BA无标度网络模型不同于随机网络模型，随机网络模型不考虑新增节点的优先连接性，从而得到的度分布是指数分布。

BA无标度网络的生成算法主要包括下面两个部分[5-15]：

1)增长：假设网络最初有m0个节点。每次加入一个新的节点，每次加入的新节点通过m(m≤m0)条新加入的连接边与网络中已有的m个节点相连。

2)优先连接：当挑选哪些节点与新加入的节点相连接时，假设与节点i相连接的概率∏(ki)都正比于节点i的度ki，

(1)

根据上述步骤重复t次后生成得到一个有N=t+m0个节点和mt条边的网络，图1举例说明了当m=m0=2时，初始网络为孤立节点的BA无标度网络的演化及过程。初始网络有两个节点，每次新增加的一个节点按优先连接机制与网络中已经存在的两个节点相连。

其度分布即节点具有度为k的概率为P(k)～2m2k-γ,γ=γBA=3,这种度分布成为无标度的幂率分布，并且标度指数γ与算法中仅有的参数m无关。

图1 BA无标度网络的演示示例

2 鲁棒性

衡量网络的鲁棒性一般有两个参数：级联失效过程中的最大连通子图大小以及渗流阈值，第一个参量的值越大，则网络的鲁棒性就越好。本文使用网络的最大连通子图规模来测量网络被攻击后的性能。

在网络A=(V，{Edge})中[16]，e和v都是网络的节点，若存在交替的顶点和边的序列，则e和v是连通的。如果网络A的每两点间都是连通，那么A就是一个连通图。若A不是连通图时，整个网络被分为若干个连通子图，而包含节点最多的子图就是最大连通子图。最大连通子图也被称为“巨组件(giant component)”，巨组件越大，则网络的连通性就越好，所以其规模也可以度量网络的性能。G表示网络的鲁棒性，定义为相继故障之后和之前，网络中最大连通子图的大小比值，即：

(2)

这里N和N′分别为相继故障发生前后的网络中最大连通子图的节点数。若G≈1,则表示网络保持完整。若G≈0，则表示受攻击后网络变为孤立节点。

3 鲁棒性与负载和攻击标度的关系

实验环境：CPU为Intel Core Duo，内存2G，操作系统为Windows XP，仿真软件为Matlab。其中整体算法如图2所示。

图2 程序的整体算法流程

下面研究网络负载w和攻击标度tao对网络鲁棒性的影响。先生成一个节点N=100，m0=5,m=2的BA无标度经典网络，见图3。

图3 节点N=100，m0=5,m=2的BA无标度经典网络

分别设置网络负载w=0(网络零负载)和w=1(网络满负载)，对多次结果进行平均统计得到图4a和图4b，从图4a可以看出对于tao=1(随机攻击)，G的值远远高于tao=0(蓄意攻击)的G值；从图4b可以看出对于不管随机攻击还是蓄意攻击，G值很快变为0。

图4 w=0和w=1时摧毁点与G关系

生成一个初始节点m0=10，m=2，网络节点数N=200，直到G小于0.1，程序结束运行。把攻击标度tao分别设为0和1，并对多次结果进行平均统计，得到图5a和图5b。从图5a可以看出对于蓄意攻击，网络满负载相对网络零负载的最大连通子图下降的较缓慢，但是被摧毁的节点数也很少降为0。从图5b可以看出随机攻击，网络满负载比网络零负载的最大连通子图下降快很多。

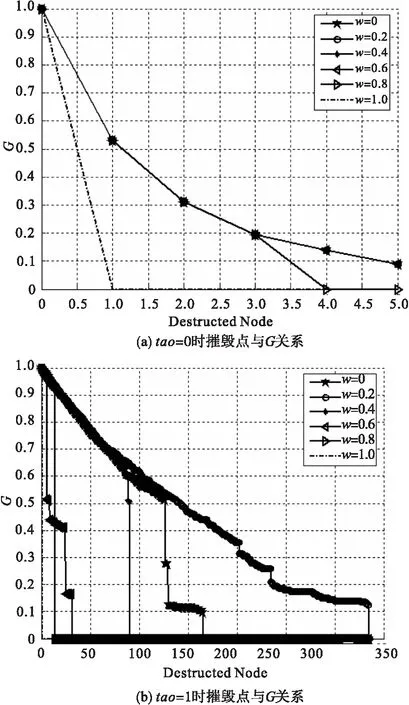
图5 tao=0和tao=1时摧毁点与G关系

综上所述，可以得到结论：(1)BA无标度网络受网络攻击标度影响较大，随着攻击标度大小的增加，网络的鲁棒性增加，当网络受到随机攻击时网络表现出很强的鲁棒性，而受到蓄意攻击时，网络的脆弱性很强；(2)BA无标度网络受网络负载影响相对网络攻击标度来的小。随着网络负载的增加，网络鲁棒性下降，当网络负载大于0.6时，网络鲁棒性很快下降，表明系统已经分裂为许多孤立的部分而无法正常工作，可以用控制网络负载变化时的网络拓扑结构的变化来分析相继故障的发生过程[17]。

4 结束语

以BA无标度网络为研究对象，给出了BA无标度网络的构造算法。用受攻击前后的最大连通子图的大小比值G作为衡量标准，研究了BA无标度网络在遭遇随机攻击和蓄意攻击后网络负载对G的影响。仿真结果证明了无标度网络对随机破坏有很高的抗毁性，而对蓄意攻击网络则显得十分脆弱。

[1] 王建伟，荣莉莉.超负荷边带有崩溃概率的相继故障模型上袭击策略研究[J].中国管理科学，2009，27(6)：247-156.

[2] 王建伟，荣莉莉，王铎.基于节点局域特征的复杂网络上相继故障模型[J].管理科学学报，2010，13(8)：42-50.

[3] 郭世译.复杂网络基础理论[M].北京：科学出版社，2012：37-38.

[4] Barabasi AL,Albert R.Emergence of scaling in random network[J].Nature,1999,393(6684):440-442.

[5] 潘灶烽.加权复杂网络的建模研究[D].上海：上海交通大学，2005.

[6] 彭刚.因特网拓扑结构复杂性研究[D].武汉：华中师范大学，2006.

[7] 何士产.复杂网络的耗散结构特征与矩阵表示研究[D].武汉：武汉理工大学，2007.

[8] 冷延东.Ad Hoc互连网络小世界特性的研究[D].南京：南京邮电大学，2008.

[9] 彭俊.复杂网络的拓扑结构及传播模型的研究[D].西安：西安电子科技大学，2009.

[10]刘自然.加反馈机制的复杂网络动力学[D].湖南：湖南师范大学，2007.

[11]田蓓蓓.复杂网络传播行为的元胞自动机模拟研究[D].上海：上海大学，2008.

[12]周杰.复杂系统中的信息传播研究[D].武汉：华中师范大学，2008.

[13]吴楠.复杂网络理论在贵州输配电网中的应用基础研究[D].贵州：贵州大学，2008.

[14]王茹.复杂网络Opinion动力学研究[D].武汉：华中师范大学，2009.

[15]黄丹.考虑代价的无标度网络攻击性研究[D].武汉：中南民族大学，2011.

[16]Moreno Y,Gomez J B,Pacheco A F.Instability of scale-free networks under node-breaking avalanches[J].Europhys.Lett.,2002,58(4):630-636.

[17]汪小帆，李翔，陈关荣.复杂网络理论及其应用[M].北京：清华大学出版社，2006:102.