部分呈现条件下类别分类学习中的信息表征机制*

2014-02-02王瑞明林哲婷刘志雅

心理学报 2014年8期

王瑞明林哲婷,2 刘志雅

(1华南师范大学心理应用研究中心/心理学院, 广州 510631) (2北京师范大学心理学院, 北京 100875)

1 引言

类别学习能力是人类的基本能力, 人类通过分类来进行信息的检索, 把纷繁复杂的世界知识进行有序的组织。当遇到新的事物或刺激时, 这种世界知识的组织方式, 将决定这些新信息如何有效地存储, 以至于决定了随后的推理或者行为反应。类别学习的研究一直备受关注, 特别是学习了某个新的类别知识后形成的类别表征(Ashby & Maddox,2005)。目前, 类别学习的研究主要有两种形式。一是分类学习, 即根据样例所具有的特征判断其类别属性。如判断空中飞翔的动物是老鹰还是苍蝇。此类研究主要探讨材料的物理特征、呈现方式、个体心理差异等对归类活动的影响。二是推理学习, 即在已知类别归属的情况下预测样例的未知特征。如已知空中飞翔的是老鹰, 可以推测它有一对翅膀。此类研究主要探讨特征典型性(Yamauchi &Markman, 2000)、因果知识(Rehder & Burnett, 2005;Hayes & Thompson, 2007)对预测准确性的影响。这两种学习任务信息加工策略不同, 分类任务使被试更为关注类别间差异信息, 推理任务则更为关注类别间的共同信息(Yamauchi, Love, & Markman,2002; 刘志雅, 莫雷, 2006)。

研究者发现有两种重要的信息参与了类别表征, 诊断性(diagnosticity)特征信息和典型性(prototypicality)特征信息(Chin-Parker & Ross, 2002;2004; 阴国恩, 李勇, 2007)。所谓诊断性特征信息,是指可以区分类别归属的特征; 典型性特征信息是类别内与样例原型一样的特征。诊断性特征倾向于成为类别内部的典型性特征, 而典型性特征却不一定可以成为诊断性特征。比如“会吠”是区分狗和猫类别的诊断性特征, 它同时也是狗的典型性特征,“短毛”是狗的典型性特征, 但却不是区分狗和猫的诊断性特征。而非诊断性特征(nondiagnostic feature)信息是指在样例中除了诊断性特征以外的典型性特征信息, 如狗的“短毛”特征。

如果把类别标签和类别特征都看成是类别的相应维度, 那么, 假如某个样例属于类别 A (或者B), 并拥有 5个类别特征, 每个特征又有两种水平(特征值0或1), 当其特征值都为0时, 即可将其表示为(A,0,0,0,0)。由此, 类别分类任务可表示为(?,0,0,0,0); 推理任务可表示为(A,0,?,0,0)。可见, 无论类别分类任务还是类别推理任务本质上都是个体根据类别的心理表征对未知的样例维度信息做出预测, 这种预测的一个关键问题是如何借助于可以区分类别归属的特征, 即诊断性特征信息(Markman & Ross, 2003)。

先前研究主要比较了分类和推理这两种不同类别学习任务的难易程度、学习的性质以及信息加工过程等(Yamauchi & Markman, 2000; Yamauchi,Love, & Markman, 2002; 刘志雅, 莫雷, 2006;2009)。Chin-Parker和 Ross (2002, 2004)的研究表明,不同的类别学习方式形成不同的心理表征。分类学习者关注类别间的区分性信息, 对诊断性特征信息更为敏感。而推理学习者则关注的是类别内的相同信息, 对典型性信息则更为敏感。而 Yamauchi和Markman (2000), Yamauchi, Love和Markman(2002)所做的有关类别学习中顺序效应的研究表明, 先进行推理学习有利于随后的分类学习, 而分类学习对于随后的推理学习则没有显著影响。也就是说, 在推理学习任务中, 可以同时学到典型性和诊断性特征信息, 而在分类学习任务中只能学到诊断性特征信息, 不能学习非诊断性特征信息(Markman &Ross, 2003)。例如, Chin-Parker和 Ross (2004)研究了类别学习中的特征诊断效应。实验材料由5个特征组成的虫子构成, 两个类别原型是重叠的(A,0,0,0,0,0)和(B,0,0,1,1,1)。所有学习的样例都只有一个特征和原型不同, 构成家族相似性结构。迁移测验的项目与原型有不同程度的重叠。例如, 某个项目3个特征和原型A重叠, 可能重叠的都是诊断性特征(A,1,1,0,0,0), 也可能重叠的有2个诊断性特征和一个非诊断性特征(A,1,0,0,0,1)。结果发现,对于分类学习者, 典型性评价主要的影响来自和原型重叠的诊断性特征的数目, 总特征重叠的数目多少几乎没有影响, 对于推理学习者, 单独的诊断性特征重叠的数目对典型性判断影响很小, 更多的是总特征重叠数目。以往研究侧重于利用选择注意假设(selective attention hypothesis)来解释这种结果(Kruschke,1992; Nosofsky & Zaki, 2002; Medin &Schaffer, 1978; Rehder & Hoffman, 2005a, 2005b;Hoffman & Rehder, 2010; Kim & Rehder, 2011), 即在注意资源有限的情况下, 分类学习导致了注意分配的不均匀, 注意资源更多地分配到了诊断性信息上, 相应的, 非诊断性信息具有的注意资源就减少了。

而 Taylor和 Ross (2009)认为需要对类别学习做一个更全面的理解, 为此, 他们针对分类学习不能学到非诊断性信息提出两种假设。一是非诊断性特征不能促进分类学习; 二是分类学习中也能够学习到非诊断性特征, 只是实验室的非自然条件难以观察到这种结果。Taylor和Ross (2009)根据第二种假设, 设计了新的类别学习任务。采用了三维立体的刺激作为材料, 由于在两维的显示屏上呈现, 必然使到刺激的背面的特征被遮挡, 并通过这种方法操纵缺失特征来进行分类学习。他们指出这种任务更接近自然的条件, 即绝大部分的事物都存在一些被遮挡了的特征。Taylor等人的研究中使用了全部呈现和部分呈现(缺失 2个特征)两种条件, 结果表明, 部分呈现条件下的分类学习也能表征典型性信息, 即分类学习任务中仍然可以学到非诊断性信息。作者用注意广度来解释这种现象, 认为由于注意的资源有限, 部分呈现条件下分类学习的被试需要注意的特征较少, 此时就有更多的注意资源分配到非诊断性特征上, 而在全部呈现条件下, 被试要注意更多的特征, 注意的广度变大, 而被试的注意资源有限, 只能将注意资源放在了作用性更大的诊断性特征上。

但是, 本研究因为, Taylor和Ross (2009)的研究中部分呈现条件下的分类学习能学会非诊断性信息, 并不是注意广度的影响, 实际上是因为被试在这种分类学习任务时也同时进行了推理学习。而推理学习是能够表征非诊断性信息的, 这样就跟先前大多数研究者认为的“推理学习任务中可以同时学到典型性和诊断性特征信息, 分类学习任务中只能学到诊断性特征信息而不能学习非诊断性特征信息”的观点相一致。

为了进一步探讨 Taylor和 Ross (2009)实验结果的真正原因, 并验证本研究的基本设想。我们设计了2个实验。实验1在重复Taylor和Ross (2009)的实验的基础上增加了“缺失1个特征”这一实验条件, 如果部分呈现条件下的分类学习能学会非诊断性信息是注意广度的影响, 那么“缺失1个特征”和“缺失2个特征”条件下非诊断性信息的变化也会有显著差异; 如果部分呈现条件下的分类学习能学会非诊断性信息是被试进行了推理学习造成的, 那么只会出现部分呈现条件下非诊断性信息有变化, 全部呈现条件下非诊断性信息没有变化。实验2则进一步确证部分呈现条件下的分类学习能学会非诊断性信息确实是被试进行了推理学习造成的。实验条件有3种, 全部呈现7个特征、全部呈现5个特征和部分呈现5个特征。前两个水平间的注意广度不同(一个水平要注意7个特征、一个水平要注意5个特征)但推理情况相同(都不需要进行推理学习)。而后两个水平间的注意广度相同(都只需要注意 5个特征)但推理情况不同(一个水平需要推理学习、一个水平不需要推理学习)。如果前两个水平在非诊断性息加工上出现差异, 则说明是注意广度的影响; 如果后两个水平在非诊断性信息加工上出现差异, 则说明是推理加工的影响。

2 实验1

在学习后的迁移材料中增加了 14个低典型的评定材料(见表1), 在重复Taylor和Ross (2009)的实验的基础上增加了“缺失 1个特征”这一实验条件,进一步探讨部分呈现条件下的分类学习中能否学会非诊断性信息以及学会非诊断性信息的原因。

2.1 方法

2.1.1 被试

大学一年级本科生 72名, 分为 3组, 每组 24人, 男女各半。

2.1.2 材料

借用了Taylor和Ross (2009)所用的实验材料,并进行了改进。包括两种虚构的昆虫, 第一类命名为“Deeger”, 第二类称为“Koozle”。这两种类昆虫均具有 6个特征维度(触角、翅膀、前肢、后脚、眼睛、尾巴), 每个维度又有两种特征, 分别用1和0表示相同维度下的不同特征。同一类别内部特征的典型性值是一样的, 但其中有 4个诊断性特征(如尾巴、前肢、眼睛、后脚)和2个非诊断性特征(如翅膀、触角), 其特征诊断力分别为 83%和 50%。“Deeger”的类别原型是 111111, “Koozle”的类别原型是000011。图1为两种类别的原型。实验1首先探讨具有相同原型的分类学习中, 缺失特征的数目是否影响分类学习的结果。

材料是两种昆虫的样例, 即“Deeger”和“Koozle”。

学习阶段, 全部呈现条件下的学习项目是 12张昆虫图片, 不包括原型。而部分呈现条件下则是在这12张图片中随机遮掉1个或2个特征作为学习项目, 缺失1个特征时总共有72个学习项目, 缺失2个特征时总共有180个学习项目。所有学习的样例只有一个特征和原型不同, 构成线性分离的家族相似性类别结构(linearly separable category,Yamauchi & Markman, 2000)。

典型性评定阶段, 样例分别是由与原型有 4个、5个和 6个相同的特征组成, 所有典型性评定阶段的样例都是完整呈现的。与原型有4个相同特征的样例称为低典型, 与原型有5个相同特征的样例称为高典型, “高典型”和“低典型”后面的数字2,3,4分别表示的是诊断性特征的数目。例如, 原型为Deeger样例 111110即可表示为高典型4。表1中所示的是实验1典型性评定的样例。

2.1.3 设计和程序

本实验采用单因素被试间设计, 自变量是材料呈现的完整性, 分为全部呈现、缺失1个特征、缺失2个特征的学习任务3种水平。

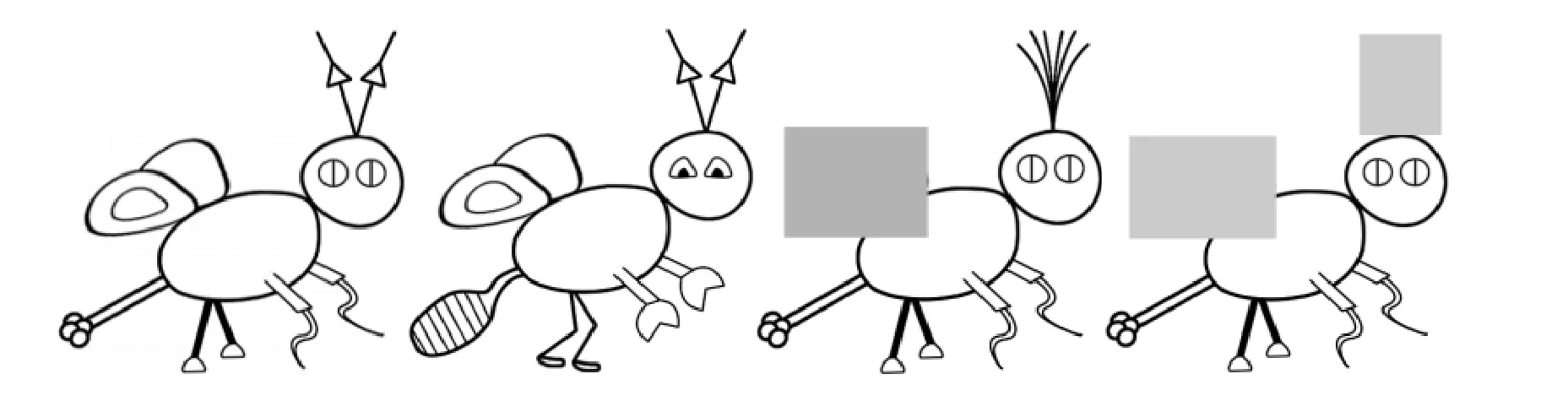
图1 实验1所用材料示例

表1 实验1中典型性评定项目

实验分为学习阶段和典型性评定阶段。在学习阶段, 屏幕呈现指导语, 被试理解后屏幕正中央开始呈现图片, 要求被试判断其为“Deeger”还是“Koozle”。如果是“Deeger”则按 D 键, 是“Koozle”则按K键, 判断后即刻给予反馈, 接着图片上方呈现正确答案, 并和图片一起保持 2s, 然后出现下一张图。类别学习的开始阶段被试只能猜测和试误,随着实验的进行, 他们会逐渐根据自己的观察和反馈信息对类别特征进行学习。不管是全部呈现还是部分呈现, 被试都被要求做完至少 50个 trial直到对连续9张图片判断完全正确为止才能达到学习标准。接下来是典型性评定阶段, 在屏幕上逐个呈现表 1中的完整样例图片和类别的标签(Deeger和Koozle), 要求被试对该图片在这个类别中的典型性进行评定。按1～7数字键反应, 数字越大代表典型性越高。

2.2 结果与分析

学习阶段：

全部呈现条件下, 被试达到学习标准平均需要83.46个trials (

=30.92), 缺失1个特征条件下需要82.96个trials (

=32.98), 缺失两个需要72.91个trials (

=19.28)。尽管缺失条件下被试达到学习标准比全部呈现条件下快, 但是三者差异不显著,

(2,69)=0.99,

>0.05。说明了3种学习条件下, 被试以相同的效率达到的相同的学习程度, 这个结果与Taylor和Ross (2009)的研究一致。

典型性评定：

实验1中各条件的典型性评定的均值见表2。

从表 2看, 3种呈现条件下都表现出了显著的诊断性信息变化, 与学习样例的原型相似在诊断性特征数目越多, 获得的典型性评价越高(表 2：4>3>2); 但是, 只有在缺失特征的条件下, 非诊断性信息的变化差异显著。表3计算出了被试在样例不同呈现形式条件下对于诊断性和非诊断性信息变化的均值与标准差。

通过学习后对新刺激(表 1)的典型性评定, 分析被试对诊断性信息和非诊断性信息的加工差异。计算诊断性信息变化下的典型性评定量的变化, 方法是求具有相同典型性但相差一个诊断性特征样例间的典型性评定均值的差, 见表 1, 计算高典型4-(减号)高典型3; 低典型4-低典型3; 低典型3-低典型2的典型性评定均值的差, 然后三者再求均值,就是诊断性变化一个等级下的典型性评定量的变化; 同理, 计算非诊断性变化下的典型性评定量的变化, 求具有相同诊断性但相差一个非诊断性特征样例间典型性评定均值的差, 即计算原型-高典型4; 高典型 4-低典型4; 高典型 3-低典型3; 然后三者再求均值, 就是非诊断性变化一个等级下的典型性评定量的变化, 结果见表3。

采用典型性评定变化量与基线值0进行t检验的方法进行差异比较。结果表明, 只有在全部呈现形式和非诊断性变化下的均值(0.04)与基线值差异不显著,

(25)=1.71,

=0.10, 说明全部呈现学习条件下, 被试对新刺激的典型性评定, 未受到非诊断性信息变化的影响。此外, 表3中其它的5组平均数与基线值的比较均显著差异。其中, 诊断性变化和全部呈现条件,

(25)=11.57,

<0.01, η=0.83;诊断性变化和缺失 1个特征条件,

(23)=7.54,

<0.01, η=0.71; 诊断性和缺失2个条件,

(21) =3.24,

<0.01, η=0.37, 说明不管是全部呈现条件还是部分呈现条件, 被试对新刺激的典型性评定,均受到诊断性变化的影响, 诊断性信息都能够促进被试进行分类学习。其中, 非诊断性变化和缺失1个特征条件,

(23)=3.01,

<0.01, η=0.28,非诊断性变化和缺失2个特征条件,

(21)=2.30,

<0.05, η=0.20, 说明部分呈现条件下, 被试对新刺激的典型性评定, 受到非诊断性变化的影响,这时候的非诊断性信息都能够促进被试进行分类学习。

表2 实验1中典型性评定各类型样例的均值

表3 不同呈现形式条件下被试判断诊断性和非诊断性信息变化的均值与标准差

3种呈现条件下诊断性变化的方差分析结果表明, 三者差异显著,

(2,69)=5.30,

<0.01, 多重比较结果说明, 全部呈现和缺失2个特征条件间的诊断性变化有显著差异：

(46)=3.18,

<0.05, η=0.18; 缺失2个和缺失1个条件下的诊断性变化也有显著差异：

(44)=2.29,

<0.05, η=0.11, 这个结果表明, 只有在缺失2个特征条件下的分类学习者才显著受到诊断性信息的变化的影响。3种呈现条件下非诊断性变化的方差分析结果表明, 三者差异显著,

(2,69)=3.73,

<0.05, 多重比较结果表明, 全部呈现<缺失1个特征=缺失2个特征,

(46)=1.87,

<0.05, η=0.07;

(44)=0.87,

>0.05, η=0.27, 即非诊断性信息(典型性信息)促进了部分呈现条件下的分类学习。

总的来说, 本实验结果符合预期, 并且与Taylor和Ross (2009)研究结果一致。证明不管是在全部呈现条件下还是缺失条件下, 被试都能够学习到诊断性特征信息, 但是, 只有在缺失条件下, 被试在做典型性评定的时候才会受到非诊断性特征变化的影响。同时还表明, 缺失2个特征条件下学习的速度最快(但差异不显著), 平均只需要 72.91个 trials就达到学习标准, 而缺失 1个特征条件下需要 82.96个 trials, 全部呈现条件需要 83.46个trials, 说明缺失特征越多, 学习效率越高。

为何缺失条件下分类学习能够加工非诊断信息, 而且学习效率还更高, Taylor和Ross (2009)研究的解释是因为注意广度的影响, 相对于全部呈现条件下, 在缺失条件下有更充分的注意资源去加工诊断性信息外的其它信息。然而, 如果被试在缺失条件下对缺失特征进行了推理, 也能够解释为何缺失条件下分类学习能够加工非诊断性息, 而且缺失的特征越多, 加工的程度越深, 这样还进一步解释了为何缺失特征越多, 学习效率反而越好。并且实验1中“缺失1个特征”和“缺失2个特征”条件下非诊断性信息的变化没有显著差异, 这也说明注意广度没有产生影响。因此实验2进一步探索缺失条件下分类学习者对非诊断性信息的加工, 是否确实是推理学习造成的。

3 实验2

学习阶段的学习材料是线性分离的家族相似性类别结构(linearly separable category, Yamauchi &Markman, 2000), 这种类别结构每个样例都和所属的原型有一个特征不同。实验1采用了全部呈现、缺失1个特征和缺失2个特征这3个水平设计, 因此这 3个学习条件的被试分别面对了 6个特征, 5个特征和4个特征的刺激进行分类学习, 所以3个条件的注意广度是不同的; 实验2改变为全部呈现7个特征, 全部呈现5个特征和部分呈现5个特征的三水平设计, 前两个水平间的注意广度不同(7个特征和 5个特征)但推理情况相同(都是全部呈现),而后两个水平间的注意广度相同(都是5个特征)但推理情况不同(全部呈现和部分呈现)。如果前者对非诊断性息加工出现差异显著, 则说明是注意广度的原因; 如果后者对非诊断性信息加工差异显著,则说明是推理加工的原因。

3.1 方法

3.1.1 被试

大学一年级本科生 60名, 分为 3组, 每组 20人, 男女各半。其中一名女生没有达到学习标准。

3.1.2 材料

实验2采用类似实验1的两类虚构的昆虫, 还是命名为“Deeger”和“Koozle”。除了保留 5 个特征维度的类别学习材料, 原型分别为11111和00011,还增加了7个特征维度的类别学习材料, 原型分别为 1111111和 0000011, 构成线性分离的家族相似性类别结构。

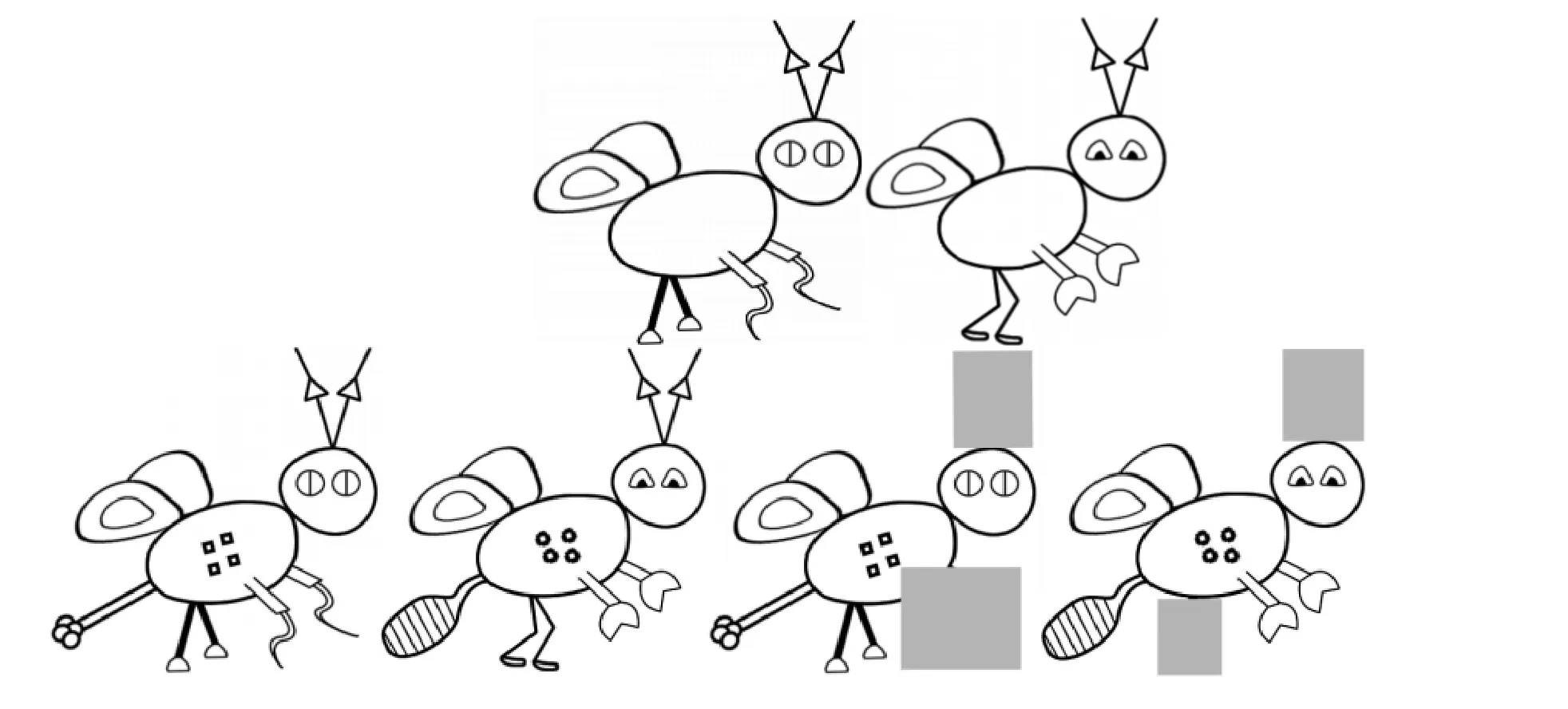
图2 实验2所用材料示例

学习阶段给予3组被试3种不同的学习材料。一为全部呈现 7个特征材料, 原型分别为 1111111和0000011的线性分离类别结构, 有14个学习样例。二为全部呈现5个特征材料, 原型分别为11111和00011的线性分离类别结构, 有10个学习样例。三为部分呈现5个特征材料, 由全部呈现7个特征材料基础上随机遮掉两个特征所得, 有 14个学习样例。

典型性评定阶段, 全部呈现 7个和部分呈现 5个的样例分别是由与原型有5个、6个和7个相同的特征组成, 所有典型性评定阶段的样例都是完整呈现的。与原型有5个相同特征的样例称为低典型性, 与原型有6个相同特征的样例称为高典型性。“高典型”和“低典型”后面的数字 3,4,5分别表示的是诊断性特征的数目。全部呈现5特征条件的样例则是由与原型有3个、4个和5个相同的特征组成。

3.1.3 设计和程序

单因素被试间设计, 自变量是材料呈现方式,分为全部呈现7个特征、全部呈现5个特征和部分呈现5个特征3种水平。

实验程序同实验1。

3.2 结果与分析

学习阶段：

学习效率分析的结果与实验1一致, 同样的表现出缺失特征条件下有最高的学习效率, 但条件间差异不显著。全部呈现7个特征条件下, 被试达到学习标准所需要的trials的平均数为85.13个(

=15.31), 全部呈现 5个条件下, 被试达到学习标准平均需要90.83个trials (

=25.14), 而在缺失2个特征的情况下, 被试学习7个特征数的类别需要76.50个trials (

=15.17)。方差分析结果表明, 三者差异不显著,

(2,56)=1.38,

>0.05。

典型性评定阶段：

同实验1。典型性评定评定了被试对诊断性信息和非诊断性信息的敏感性, 其计算方法也和实验1的类似。在本实验中, 具有 7个特征的类别的诊断性变化相当于高典型5-高典型4, 低典型5-低典型 4, 低典型 4-低典型 3的均值, 非诊断性变化则是原型-高典型 5, 高典型 5-低典型 5, 高典型 4-低典型4三者的均值, 而具有5个特征的类别的诊断性变化为高典型3-高典型2, 低典型3-低典型2, 低典型 2-低典型 1的均值, 非诊断性变化是原型-高典型3, 高典型3-低典型3, 高典型2-低典型2的均值, 具体见表4。

3种条件下都表现出了显著的诊断性信息的变化, 但是只有在部分呈现5个特征的条件下才出现非诊断性信息的变化差异显著。在样例不同呈现形式条件下对于诊断性和非诊断性信息变化的均值与标准差见表5。

同样采用典型性评定变化量与基线值0进行t检验的方法进行差异比较。非诊断性变化与基线值0的差异进行t检验时发现, 全部呈现形式, 包括全部呈现7个和全部呈现5个, 非诊断性变化下的均值(0.04, 0.32)与基线值差异不显著,

(22)=0.29,

>0.05,

(17)=2.10,

>0.05; 部分呈现形式非诊断性变化下的均值(0.25)与基线值差异显著,

(17) =2.80,

<0.05, η=0.31。结果说明, 注意广度不同但推理情况相同的前两个条件都没有加工非诊断性信息, 而注意广度相同但推理情况不同的后两个条件则不同, 其中全部呈现5个条件没有加工非诊断性信息, 而部分呈现5个条件加工了诊断性信息。这个结果说明缺失条件下分类学习者对非诊断性信息的加工, 不是注意广度造成的, 而是推理学习造成的。

表4 实验2中典型性评定各类型样例的均值

表5 不同呈现形式条件下对于诊断性和非诊断性信息变化的均值与标准差

此外, 诊断性变化与基线值0进行比较时都有显著差异。全部呈现 7个条件下：

(22)=7.55,

<0.01, η=0.74; 全部呈现5个下：

(17)=5.28,

<0.01, η=0.62; 部分呈现 5个条件下：

(17) =4.73,

<0.01, η=0.56。这个结果和实验1一致, 说明3种学习条件下被试均能够习得诊断性信息。

4 讨论

4.1 部分呈现条件下的分类学习者能够学习非诊断性信息

以往研究认为, 在类别学习任务中, 分类学习者只对诊断性信息敏感, 而推理学习者对于典型性信息(包括诊断性和非诊断性信息)更加敏感。在这些研究中, 实验材料往往是完整呈现的, 然而, 在日常生活中, 我们对物体进行分类和预测时常常不能了解到该物体的全部特征, 如看到一只狗, 我们知道它有 4条腿, 两只眼睛, 会跑会跳, 但是我们并不清楚它是公的还是母的, 它是什么品种等, 不过, 这并不影响我们对它进行分类。

我们基本沿用了 Taylor和 Ross (2009)所用的研究范式, 采用缺失特征的材料进行实验, 并对材料进行了改进, 验证了部分呈现条件下的类别分类学习的学习者也是能够学习到非诊断性信息的。所以, 不仅在推理学习中可以学习到非诊断性信息,而且在部分呈现条件下的分类学习也可以。

4.2 全部呈现和部分呈现条件下的分类学习导致不同的类别表征

本研究中采用的类别结构是线性分离类别结构, 在类别内部每个特征维度只有一个成员的特征值是例外的。对于部分呈现条件下的分类学习者,由于特征缺失, 学习者将注意力转移到每个类别内的成员的所有特征, 包括诊断性和非诊断性特征,学习到关于类别的典型性信息, 即包括了诊断性信息和非诊断性信息。而全部呈现条件下的分类学习者主要关注诊断性信息, 在所有特征都呈现的情况下, 被试记住所有呈现的特征会比较困难, 诊断性特征能使类别判断具有较高的正确率, 此时, 虽然诊断性信息和非诊断性信息是同时出现的, 但是,非诊断性信息却没有被分类学习者纳入到他们的类别表征中。

结合前人研究结果, 特别是分类和推理两种学习模式比较研究(刘志雅和莫雷, 2006; 2009), 我们推测认为, 全部呈现条件下的分类学习可能是一种自下而上的归纳加工方式, 对个别性的特征信息进行加工, 进而习得一般性的类别知识; 而部分呈现条件下的分类学习则类似于推理学习的模式, 可能是一种自上而下的演绎加工方式, 先对一般性信息和若干个别性的特征信息进行加工, 进一步推导某些个别性的特征信息。

4.3 全部呈现条件下的分类学习结果与类别原型的特征数无关

本两个实验中, 在全部呈现条件下, 不管样例的原型有7个、6个还是5个特征, 被试达到学习标准所需要的 trial数并没有差异显著,

(2,61) =0.98,

>0.05。而这几种条件下的原型所具有的诊断性特征都只有 2个, 这从另一个角度说明了, 全部呈现条件下的学习结果跟全部的特征数无关, 而与诊断性特征有关。这个结果不支持原型理论的假设。原型理论认为(Rosch & Mervis, 1975; Markman& Wisniewski, 1997; Kim & Murphy, 2011), 类别学习实质上是学习类别的原型。当遇到一个新的样例时, 哪个类别的原型与之最相似, 人们会把它归类到这个类别之中。全部呈现条件下, 原型有7个特征的家族相似性类别结构里, 原型特征的典型性最高, 为12/14; 原型有6个特征的次之, 为10/12; 原型有5个特征的最低, 为8/10。如果类别学习的学习结果是原型, 不同典型性类别结构的学习效率应该存在显著的差异, 而 2个实验的结果表明, 不管样例的原型有7个、6个还是5个特征, 被试达到学习标准所需要的trial数并没有显著的差异, 与原型理论的假设不一致。

4.4 部分呈现条件下的分类学习者进行了推理加工

本研究结果表明, 全部呈现条件和部分呈现条件下的分类学习者对于非诊断性信息的敏感程度不同, 部分呈现条件下的分类学习者对非诊断信息的变化敏感, 这种信息表征上的差异究竟是来自心理机制本身, 还是决定于外在的学习形式, 或者两者同时起作用, 这是我们比较关注的问题。

Taylor和Ross (2009)的研究中只使用了全部呈现和部分呈现(缺失 2个特征)两种条件, 发现部分呈现条件下的分类学习仍然可以学会非诊断性信息, 并用注意广度来解释这种现象, 认为由于注意的资源有限, 部分呈现条件下分类学习的被试需要注意的特征较少, 此时就有更多的注意资源分配到非诊断性特征上, 而在全部呈现条件下, 被试要注意更多的特征, 注意的广度变大, 而被试的注意资源有限, 只能将注意资源放在了作用性更大的诊断性特征上。

本研究实验1在重复Taylor和Ross (2009)的实验的基础上增加了“缺失 1个特征”这一实验条件,如果部分呈现条件下的分类学习能学会非诊断性信息是注意广度的影响, 那么“缺失 1个特征”和“缺失2个特征”条件下非诊断性信息的变化就会有显著差异。实验结果发现, 只有部分呈现条件下非诊断性信息有变化, 全部呈现条件下非诊断性信息没有变化, 这跟Taylor等人的研究结果一致, 但是“缺失1个特征”和“缺失2个特征”条件下非诊断性信息的变化没有显著差异, 这说明注意广度没有产生影响。

实验1虽然证明了部分呈现条件下被试非诊断性信息的学习不是注意广度造成的, 但还不能充分说明就是推理学习造成的, 因此本研究又设计了实验2, 对这一问题进行进一步的探讨。

实验2中自变量有全部呈现7个特征、全部呈现5个特征和部分呈现5个特征3种水平。前两个水平间的注意广度不同(一个水平要注意7个特征、一个水平要注意5个特征)但推理情况相同(都不需要进行推理学习)。而后两个水平间的注意广度相同(都只需要注意5个特征)但推理情况不同(一个水平需要推理学习、一个水平不需要推理学习)。如果前两个水平在非诊断性息加工上出现差异, 则说明是注意广度的影响; 如果后两个水平在非诊断性信息加工上出现差异, 则说明是推理加工的影响。实验结果是在全部呈现7个特征和全部呈现5个特征的条件下, 被试都没有学会非诊断性信息, 而只有在部分呈现5个特征的条件下, 被试才学会了非诊断性信息。也就是说, 注意广度不同但推理情况相同前两个条件都没有加工非诊断性信息, 而注意广度相同但推理情况不同的后两个条件则不同, 其中全部呈现5个条件没有加工非诊断性信息, 而部分呈现5个条件加工了诊断性信息。这个结果说明缺失条件下分类学习者对非诊断性信息的加工, 不是注意广度造成的, 应该是推理学习造成的。

综合所有实验结果, 可以认为, 部分呈现条件下的分类学习者进行了推理加工, 由于推理学习能够表征非诊断性信息, 因此, 在部分呈现条件下的分类学习者能够学习到非诊断性信息。部分呈现条件下, 学习者不可能只关注一个或两个维度上的特征就能够顺利进行分类, 因为学习过程中出现的样例是不完整的, 学习者在关注其他特征信息的同时可能对缺失的特征进行了推理加工。

本研究通过2个实验证明了部分呈现条件下的分类学习中可以表征非诊断性信息, 并且这种非诊断性信息的表征不是注意广度造成的, 而是引发被试进行了推理学习造成的。当然, 部分呈现条件下分类学习中被试能够表征非诊断性信息是被试进行了推理学习的观点还需要进一步的实验证据, 特别是这种推理学习是自动化进行的还是策略性发生的, 还需要在以后的研究中进一步探讨。

5 结论

全部呈现条件下和部分呈现条件下分类学习任务中的被试能够学习到诊断性信息, 但只有部分呈现条件下的分类学习能够表征非诊断性信息, 这种实验结果不是由于注意的广度造成的, 而是因为被试在部分呈现的分类学习中进行了推理加工。

Ashby, F. G., & Maddox, W. T. (2005). Human category learning.

Annual Review of Psychology, 56

, 149–178.Chin-Parker, S., & Ross, B. H. (2002). The effect of category learning on sensitivity to within category correlations.

Memory & Cognition,30

(3), 353–362.Chin-Parker, S., & Ross, B. H. (2004). Diagnosticity and prototypicality in category learning: A comparison of inference learning and classification learning.

Journal of Experimental Psychology: Learning, Memory, and Cognition,30

(1), 216–226.Taylor, E. G., & Ross, B. H. (2009). Classifying partial exemplars: Seeing less and learning more.

Journal of Experimental Psychology: Learning, Memory, and Cognition,35

(5), 1374–1380.Hayes, B. K., & Thompson, S. P. (2007). Causal relations and feature similarity in children’s inductive reasoning.

Journal of Experimental Psychology

General, 136

, 470–484.Hoffman, A. B., & Rehder, B. (2010). The costs of supervised classification: The effect of learning task on conceptual flexibility.

Journal of Experimental Psychology: General,139

(2), 319–340.Kim, S. W., & Murphy, G. L. (2011). Ideals and category typicality.

Journal of Experimental Psychology: Learning,Memory, and Cognition, 37

(5), 1092–1112.Kim, B., & Rehder, B. (2011). How prior knowledge affects selective attention during category learning: An eyetracking study.

Memory & Cognition, 39

(4), 649–665.Kruschke, J. K. (1992). ALCOVE: An exemplar-based connectionist model of category learning.

Psychological Review, 99

, 22–44.Nosofsky, R. M., & Zaki, S. R. (2002). Exemplar and prototype models revisited: Response strategies, selective attention, and stimulus generalization.

Journal of Experimental Psychology: Learning, Memory, andCognition, 28

, 924–940.Markman, A. B., & Wisniewski, E. J. (1997). Similar and different: The differentiation of basic level categories.

Journal of Experimental Psychology: Learning, Memory &Cognition,23

(1), 54–70.Markman, A. B., & Ross, B. H. (2003). Category use and category learning.

Psychological Bulletin, 129

(4), 592–613.Medin, D. L., & Schaffer, M. (1978). Context theory of classification learning.

Psychological Review,85

(3),207–238.Liu, Z. Y., & Mo, L. (2006). A comparative study of two types of category learning: Classification and inference learning.

Acta Psychologica Sinica, 38

(6), 824–832.[刘志雅, 莫雷. (2006). 类别学习中两种学习模式的比较研究: 分类学习与推理学习.

心理学报,38

(6), 824–832).]Liu, Z. Y., & Mo, L. (2009). Prototype and exemplar on classification and inference learning.

Acta Psychologica Sinica, 41

(1), 44–52.[刘志雅, 莫雷. (2009). 两种学习模式下类别学习的结果:原型和样例.

心理学报, 41

(1), 44–52.]Rehder, B., & Burnett, R. C. (2005). Feature inference and the causal structure of categories.

Cognitive Psychology,50

(3),264–314.Rehder, B., & Hoffman, A. B. (2005a). Thirty-something categorization results explained: Selective attention,eyetracking, and models of category learning.

Journal of Experimental Psychology: Learning, Memory, and Cognition, 31

, 811–829.Rehder, B., & Hoffman, A. B. (2005b). Eyetracking and selective attention in category learning.

Cognitive Psychology, 51

, 1–41.Rosch, E., & Mervis, C. B. (1975). Family resemblances:Studies in the internal structure of categories.

Cognitive Psychology, 7

, 573–605.Yamauchi, T., & Markman, A. B. (2000). Inference using categories.

Journal of Experimental Psychology: Learning,Memory, and Cognition,26

(3), 776–795.Yamauchi, T., Love, B. C., & Markman, A. B. (2002) Learning nonlinearly separable categories by inference and classification.

Journal of Experimental Psychology:Learning Memory, and Cognition,28

(3), 585–593.Yin, G. E., & Li, Y. (2007). Effect of feature diagnositicity on category use.

Acta Psychologica Sinica,39

(5), 819–825.[阴国恩, 李勇. (2007). 类别使用的特征诊断效应.