采用分割频带法构造宽间隔跳频序列
2014-02-01赵洪林
韩 明,赵洪林
(哈尔滨工业大学 通信技术研究所,哈尔滨 150001)
1 引 言
跳频通信具有抗干扰能力和低截获概率等特点,被广泛应用于保密通信领域。跳频通信的发射频率受到跳频序列的控制,跳频序列对系统抗干扰性能优劣起决定性作用。若电台在某一载频上持续时间过长,受到干扰的概率将大大增加。如果把序列调整成宽间隔的,性能将有所提升。宽间隔跳频在对抗单频干扰、部分频带干扰、跟踪干扰、多径衰落等方面均有优势[1]。
国内陈文德首先提出了宽间隔处理的思想,介绍了去中间频带法[2]。1999年何维苗提出随机平移替代法[3]。2002年梅文华、张志刚将L-G模型与对偶频带法结合构造出性能优良的跳频序列族[4],确立了对偶频带法的经典地位。文献[5-6]曾分别对构造跳频序列的不同方法结合对偶频带法进行了探讨。2007年,李金涛基于m序列,提出非线性模d法[7],性能有所提升,但远不及对偶频带法经典和实用。文献[8]针对RS码跳频序列,运用此方法进行了宽间隔化。文献[9]提出模d加余法。2011年,张鸿儒曾试图对对偶频带法进行改良[10],但收效很小。文献[11]也采用非线性处理方法对其进行了优化,但平衡性下降。2013年,冯建利、赵裔昌对随机平移替代法作了改进[12]。由于对偶频带法经典实用,对其改进变得困难,文献较少,到目前为止,没有实质性进展,但对偶频带法存在保密性差的缺点。
针对这种情况,本文分析了对偶频带法的缺点,进行了优化,在继承其优秀思想的前提下,提出了随机特性增强的分割频带法,着力提高对偶频带法的保密性。
2 跳频序列的性能参数
跳频序列的性能好坏主要通过周期汉明相关性、平衡特性和跳频间隔特性3个参数来表征[1]。
(1) 周期汉明相关性
周期汉明相关表示两个序列的频率碰撞次数,是衡量跳频序列优劣的最重要指标。
若Su={su(j)}和Sv={sv(j)}分别为频率集合F上两个周期长度为L的跳频序列,当相对时延τ时,这两个序列在一个周期内的汉明相关性能可用公式(1)来描述。
(1)
其中,j+τ需要以模L运算,并且
(2)
式中,u=v时称自相关,表征同一用户各多径信号的相互干扰;u≠v时称互相关,表征不同用户信号的频率碰撞。
(2) 平衡特性
平衡特性描述一个跳频序列周期中各频点的分布情况,公式(3)给出了平衡特性δ的定义,δ越小,表示更均匀的频点分布,更优的抗干扰性能。
(3)
式中,N为频点数目,L为跳频序列周期长度,ni为一个跳频周期中频率点fi出现的次数。
(3) 跳频间隔特性
跳频间隔分为最小跳频间隔和平均跳频间隔,表征它们的参数分别以公式(4)和公式(5)定义。宽间隔跳频是指dmin大于某一值。
(4)
(5)
3 对偶频带法
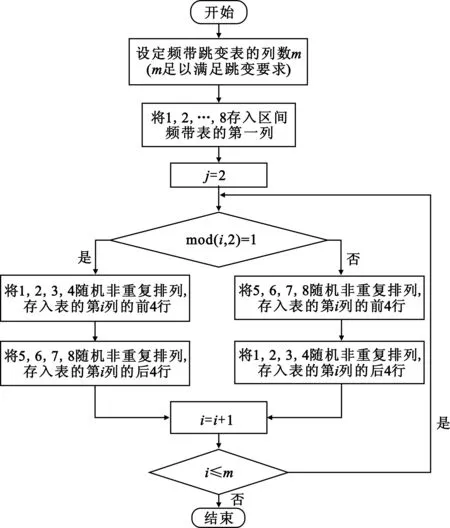
构造宽间隔跳频序列通常是采取先产生一般跳频序列,再进行宽间隔处理的方法,如图1所示。

图1 宽间隔跳频序列生成过程
Fig.1 Process of generating FH sequences with given minimum gap
本文将利用混沌算法生成一般的跳频序列然后宽间隔处理。近年来,人们一直致力于混沌序列的构造研究[13],这里使用比较成熟的优化的cos映射法,文献[6]中有详细介绍,此处不赘述,该方法构造的序列周期长度与给定的频点数相同。下面简单介绍对偶频带法的实现过程。
若给出的跳频频段区间为F,其频率数目为N,要求设计间隔不小于d的跳频序列,为简化问题,假定N为偶数。
(1) 将F分为两个区间频段F1、F2,其中
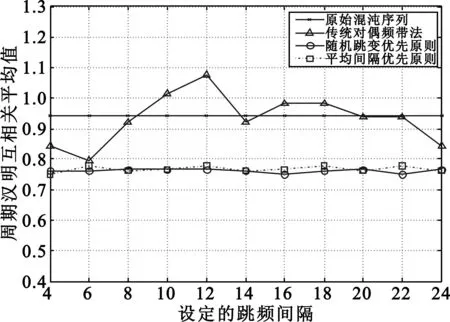
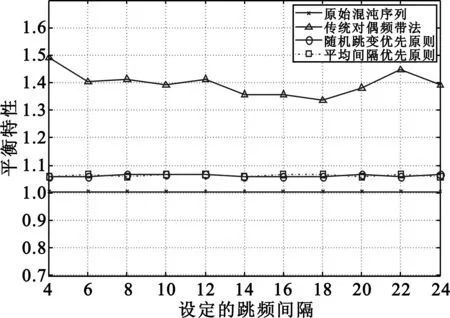
F1={fi,0≤i (6) F1和F2中的频点存在对偶关系,从而组成频率对(fi,fi+N/2),0≤i (2)在F1上从频点fi开始构造跳频序列,当要跳到的频点频率间隔小于d时,就改变路径,跳频到F2上具有对偶关系的频点,之后将在F2上跳变,再出现相同情况时,又跳回到F1上对应频点,如此继续下去,形成周期为L1(L1=N/2)的宽间隔序列。 (3)因为跳频序列首尾是相连的,当首尾频点不满足宽间隔要求时,可将某一个已满足宽间隔的频点改跳到对偶频带上。 Matlab仿真,初始值0.1(混沌算法限制在区间(-1,1)内,无特殊要求)、频点数目256、频率间隔8时构造的宽间隔混沌序列如图2所示,原始序列与宽间隔序列性能对比如表1所示。 由表1可知,经对偶频带法处理,序列在基本不改变相关特性的同时,满足了宽间隔的要求。但是表1和图2同样揭示了对偶频带法的缺点:首先,频带间跳变规律简单,易被破解,保密性差;另外,一般可用频点的数量固定,宽间隔处理后序列周期长度变为原来的一半,周期越短,越容易被截获,这一点是极其不利的;最后,宽间隔序列的平衡特性降低,一些频点没有被使用。 尽管有以上缺点,对偶频带法依旧以其性能良好、易于实现的优势成为宽间隔处理的经典方法。文献[10]改进对偶频带法,着眼于构造更多的序列从而增加保密性,通过在序列族中搜索满足宽间隔要求的频点,以达到产生更多跳频序列的目的,但效果不明显,其他性能也未提升;文献[11]改进时采用非线性处理的方法,改动较大,增加了复杂度,却降低了序列平衡性。本文优化原则为,在尽可能少地改变原来方法的基础上,克服对偶频带法保密性差等缺点,提出了融入随机特性的分割频带法。 表1 混沌序列及其宽间隔序列性能对比Table 1 The comparison of performance between chaotic sequences and its wide interval sequences 分割频带法继承了对偶频带法的核心思想,若给定的跳频频段区间为F,其中频点数为N,要求设计间隔不小于d的跳频序列。其思路是将频带F平均分割成k(正整数)个区间频带,分别记为Fj(1≤j≤k),每个频段含有N/k个频点。类似对偶频率法构造频率对,Fj中的各频点相互对应,即F1中频点fi(0≤i 分割频带法的具体实现方法因所关注的问题不同而有所差异,主要取决于区间频带表的设计,下面分别介绍随机跳变优先和平均间隔优先。 随机跳变优先原则在跳频序列满足最小间隔的前提下,优先考虑跳变的随机性。基本思想是在区间频带Fj跳变,不满足宽间隔要求时,就选择其余7个频带中的一个,跳变到对应频点,跳变规律可由区间频带表控制。 构造随机跳变优先宽间隔序列的基本步骤是: (1)构造区间频带表,算法流程如图3所示; 图3 生成随机跳变优先区间频带表的算法流程Fig.3 Flow chart of generating a frequency band table with randomness prior (2)在F1从频点fi(0≤i (3)当跳到最后一个元素时,转而依次从F2~F8中与fi对应的频点按照步骤2中所指定的规则跳变,只是若从频带Fj开始跳变,在查表时查询的是区间频带表第j行的信息。这样,又形成了7行长度为L′的跳频序列; (4)将生成的8行跳频序列依次存入表F_table中,然后将F_table中的频点按行排成一行即形成周期为L(L=8L′=N)的跳频序列; (5)除对偶频带法所规定的首尾频点要宽间隔外,在表F_table中,需要检查每一行第一个元素和前一行最后一个元素是否满足宽间隔,不满足时,则随机产生一组非重复区间频带,将表F_table中最后一列频率改跳到对应的区间频带上,接着继续检查是否满足宽间隔要求,若不满足重复以上过程,直到满足要求为止,并记录满足要求的这组区间频带,便于将来序列重复产生。 可见,步骤5中使用的方法与对偶频带法有较大差异,因为若用原来的办法解决分割频带法中的问题,不仅复杂、效率低,而且查表时区间频带表的原有规则将被破坏,可能带来周期汉明自相关性能的降低,导致抗多径干扰能力的下降。 平均间隔优先原则在跳频序列满足最小间隔的前提下,优先考虑序列的平均间隔,以使平均间隔增大,实际上此方法在平均间隔和随机性方面寻求折衷。其基本思想是将区间频带分为A={F1,F2,F3,F4}和B={F5,F6,F7,F8}两部分,若在A中的某个频点跳变,不满足频率间隔要求时,就改变路径,选择{F5,F6,F7,F8}中的一个频带,跳变到对应频点;若在B中的某个频段跳变,不满足频率间隔要求时,就改变路径,选择{F1,F2,F3,F4}中的一个频带,跳变到对应频点。 平均间隔优先原则和随机跳变优先原则产生跳频序列的步骤相同,只是所使用的区间频带表不同。产生平均间隔优先区间频带表的算法流程如图4所示。 图4 生成平均间隔优先区间频带表的算法流程Fig.4 Flow chart of generating a frequency band table with average interval prior 由分割频带法的实现步骤可以看出其继承了对偶频带法的经典思想,同时又有自身的特点: (1) 分割频带法完全是对偶频带法的延伸,在每一个小的区间频带,分割频带法与对偶频带法均具有原始混沌序列的特性,从理论上讲,其汉明相关性应与混沌序列、对偶频带法宽间隔序列基本相同。作为跳频序列最重要参数,汉明相关性不恶化是优化的前提,若以增加频率碰撞为代价来换取其他性能的提升,得不偿失; (2) 分割频带法最显眼的一点是,此方法中融入了随机特性,使用了带有明显随机性质的区间频带表。频带之间的跳变与对偶频带法简单规则不同,存在多种选择,如果不加控制,很可能导致一个周期中不同时刻跳到相同的区间频带,从而使得周期汉明自相关性能骤降,抗多径干扰能力严重破坏。分割频带法中使用精心设计的区间频带表完全避免了这些问题,同时又不失随机特性,极大地增强了保密性。区间频带表的引入,是分割频带法的最关键部分,也是其精髓所在; (3) 序列周期长度较原始序列不会改变,按顺序从各区间频带起跳,然后将得到的序列串成一行,保证了跳频周期长度,较对偶频带法具有更强的抗干扰和低截获能力; (4) 由于划分了更多的频带,跳频序列中频点使用情况将更均匀,平衡特性会有所改善。 当然,存储区间频带表需要更多的硬件资源,在硬件存储空间不断扩展的今天,这已经不构成限制。另外,序列平均间隔可能降低,但这对其抗干扰性能影响较小。 根据分割频带法的实现步骤和4.3节中的分析,分割频带法在序列随机性和周期长度方面优势很好理解,但汉明相关性和平衡性需进一步仿真验证。 利用Matlab进行仿真,设定可用频点数256,均分为8个区间频带,序列的初始值为0.1,涉及到互相关时,另一序列初始值为0.3。以上参数除初始值由混沌算法限制在区间(-1,1)外,均无特殊要求。为统一指标比较,对偶频带法的数据均化归到周期256,即原始数据做乘以2处理。设定不同的跳频间隔,各跳频序列的性能对比如图5~7所示,可以直观看出随机跳变优先原则和平均间隔优先原则构造出的序列性能基本相同,正如4.3节中所分析的那样,相对于传统对偶频带法,分割频带法在汉明相关性能基本不改变的前提下,平衡特性显著改观,已接近原始混沌序列;另外,汉明相关性能较稳定,没有大的波动,有利于避免大的突发碰撞。 图5 周期汉明自相关旁瓣性能Fig.5 Performance of cycle Hamming autocorrelation sidelobe 图6 周期汉明互相关性能Fig.6 Performance of cycle Hamming cross-correlation 图7 平衡性能Fig.7 Performance of balance 本文重点研究了构造宽间隔跳频序列的方法,介绍了经典的对偶频带法,将混沌算法与宽间隔处理方法相结合构造出宽间隔混沌序列,分析了对偶频带法的缺点。在尽可能少地改变对偶频带法的情况下对其进行优化,提出了分割频带法。该方法继承了对偶频带法的核心思想,不恶化序列的汉明相关性能,这是一切优化的前提。分割频带法根据不同的需求,设计了随机跳变优先和平均间隔优先两种区间频带表,以控制频带间的跳变规律。区间频带表的引入使得频带间跳变具有随机性,增强了序列的保密性,这是分割频带法的关键思想。另外,使用分割频带法设计出的宽间隔序列周期长度与原始序列相同,平衡性较对偶频带法也有明显提升。本文着力增强了跳频序列的保密性和平衡性,而在此基础上提高汉明相关性能、减少频率碰撞将是下一步工作的重点。 [1] 梅文华,王淑波,邱永红,等.跳频通信[M].北京:国防工业出版社,2005:72-80. MEI Wen-hua,WANG Shu-bo,QIU Yong-hong,et al.Frequency Hopping Communication[M].Beijing:National Defense Industry Press,2005:72-80.(in Chinese) [2] 陈文德.宽间隔的跳频图样[J].系统科学与数学,1983,3(4):295-303. CHEN Wen-de.Frequency Hopping Patterns with Wide Intervals[J].Systems Science and Mathematical Sciences,1983,3(4):295-303.(in Chinese) [3] 何维苗.一种新的实现宽间隔跳频的方法——随机平移替代法[J].现代军事通信,1999,7(4):13-15. HE Wei-miao.A New Method of Generating FH Sequences with Given Minimum Gap——Method of Random Shifted Replace[J].Modern Military Communications,1999,7(4):13-15.(in Chinese) [4] 梅文华,张志刚.一类新的宽间隔跳频序列族的构造[J].电波科学学报,2002,17(1):16-20. MEI Wen-hua,ZHANG Zhi-gang.Construction of families of FH sequences with given minimum gap[J].Chinese Journal of Radio Science,2002,17(1):16-20.(in Chinese) [5] Wu G,Wang D.Design and performance investigation on frequency hopping sequence with minimum gap based on RS Code[C]//Proceedings of 2010 International Conference on Electrical and Control Engineering.Wuhan:IEEE,2010:5120-5123. [6] 牛犇,李文臣.一种新的混沌宽间隔跳频序列的构造方法及其Matlab仿真分析[J].南开大学学报(自然科学版),2005,38(3):49-52. NIU Ben,LI Wen-chen.A new method for generating chaotic FH sequences with given minimum gap and their performance analysis with Matlab[J].Acta Scientiarum Naturalium Universitatis Nankaiensis,2005,38(3):49-52.(in Chinese) [7] 李金涛,汪晓宁,王祎,等.基于 m 序列的宽间隔跳频序列的生成[J].电讯技术,2007,47(3):36-40. LI Jin-tao,WANG Xiao-ning,WANG Wei,et al.Frequency Hopping Sequences with Given Minmium Gap Based on m Sequence[J].Telecommunication Engineering,2007,47(3):36-40.(in Chinese) [8] 赵珂,阳文峰,谢国锋.基于非线性取模法构造宽间隔跳频序列研究[J].南昌航空大学学报(自然科学版),2013,27(2):52-57. ZHAO Ke,YANG Wen-feng,XIE Guo-feng.Based on Nonliner Modulo Method Structure of Wide Interval Frequency Hopping Sequence[J].Journal of Nanchang Hangkong University(Natural Sciences),2013,27(2):52-57.(in Chinese) [9] Zhang H Q.Frequency hopping sequences with given minimum gap[C]//Proceedings of 2010 2nd International Conference on Future Computer and Communication.Wuhan,IEEE:2010:V3-611-V3-614. [10] 张鸿儒.构造宽间隔跳频序列方法的研究[D].成都:西南交通大学,2011. ZHANG Hong-ru.Research on frequency-hopping sequence with given minimum gap[D].Chengdu:Southwest Jiaotong University,2011.(in Chinese) [11] 冯建利,范昕.基于双素数序列的非线性宽间隔跳频序列[J].探测与控制学报,2013,35(5):83-88. FENG Jian-li,FAN Xin.Nonlinear Frequency Hopping Sequences with Given Minimum Gap Based on Double Prime Sequence[J].Journal of Detection & Control,2013,35(5):83-88.(in Chinese) [12] 冯建利,赵裔昌.一类改进的随机平移替代法构造的宽间隔跳频序列[J].电讯技术,2013,53(9):1175-1179. FENG Jian-li,ZHAO Yi-chang.Frequency Hopping Sequences with Given Minimum Gap Generated by Improved Random Shift Replace Method[J].Telecommunication Engineering,2013,53(9):1175-1179.(in Chinese) [13] Liu X,He X,Xueye A N G,et al.A New Chaotic FH Sequences Generator based On Dynamic Quantization[J].Journal of Communications and Information Sciences,2011,1(1):49-55.
4 对偶频带法的优化——分割频带法
4.1 随机跳变优先原则

4.2 平均间隔优先原则
4.3 分割频带法的特点分析
5 Matlab仿真分析

6 结 论
