双向多中继协同通信系统的性能分析
2014-02-01芮国胜
王 林,芮国胜,张 洋
(海军航空工程学院 电子信息工程系,山东 烟台 264001)
1 引 言
中继协同通信技术允许无线网络中不同用户节点共享彼此的天线和其他网络资源,形成虚拟的MIMO信道从而获得空间分集,可增大无线网络通信容量,并提高复用增益。该技术在抗信道多径衰落、扩大无线通信系统的有效覆盖半径及增强特定区域数据速率等方面也有很多优点,目前已经成为一个重要的研究热点[1-3]。然而,目前基于单向中继的协同通信系统在提高边缘用户性能的同时,却浪费了时隙资源,这样就损失了频谱效率。为此,学者提出了基于放大转发(Amplify-and-Forward,AF)和解码转发(Decode-and-Forward,DF)协议下的双向中继机制[4]。Nam等人则在此基础上,推导出了双向单中继系统的信道容量,表明了双向中继系统具有更高的频谱效率[5]。
目前,多数的双向中继理论研究还是基于单中继和两用户节点的三节点模型,多中继的系统模型研究较少。文献[6]研究了多中继节点下基于AF机制的中继选择算法;文献[7]则根据中继译码能力将多中继节点分为不同类型,推导出了DF模式下的容量;文献[8]研究了单中继节点模型AF机制下的中断概率;文献[9]对PSK调制方式下单中继节点模型的平均误码率进行理论分析,并进行了功率优化分配。上述文献中并没有对多中继节点下的AF机制的容量、中断概率、平均误码率等指标进行完整的理论分析。本文重点研究AF机制下多个中继且所有节点都为单天线的双向中继协同通信系统的性能分析,对其信道容量、中断概率、平均误码率等表达式进行理论公式推导,并与单中继的双向中继协同系统进行仿真比较,验证了双向多中继协同通信系统的优越性。
2 系统模型
双向多中继协同通信系统的传输模型如图1所示,此模型具有通用性。两个用户节点U1与U2通过多个中继节点(R1,R2,…,Rn)互换信息,假设所有的节点单元均配置单天线且工作在半双工模式,节点U1与U2之间没有直达链路,所有信道均为准静态独立的频率非选择性瑞利衰落信道。由于时分双工模式下信道的两个时隙较短,因此不失一般性,假设信道具有互易性,即从节点U1到中继节点Ri和中继节点Ri到U1的信道增益相同并设为gi,从节点U2到中继节点Ri和中继节点Ri到U2的信道增益相同并设为hi。为方便对模型性能进行研究,假设两用户节点的发射功率相同且均记为p,中继节点Ri的发射功率记为pi。考虑AF机制下的中继转发,两用户节点可以通过信道估计等方法获取所有的信道状态信息(Channel State Information,CSI)。

图1 双向多中继传输模型Fig.1 The two-way mulit-relays system model
传输全过程分为两个时隙完成,在第1个时隙内,两用户节点U1与U2同时将各自的信息s1与s2发往中继节点Ri,此时中继节点Ri接收到的信号可表示为
yi=gis1+his2+ni
(1)
其中,ni为中继Ri上的零均值、单位方差加性白高斯噪声。在第2个时隙中,参与放大转发信息的各中继节点Ri(i=1,2,…,n)把各自收到的信号乘以各自的放大增益,再把乘积得到的信号发送出去。每个中继Ri的放大增益可表示为ai,其发送的信号为
xi=aiyi=aigis1+aihis2+aini
(2)
式中,ai是基于中继Ri前后链路的信道统计信息获得的增益[10],且受限于节点发射功率pi,即ai可表示为
(3)
于是U1与U2接收到的信息分别为
(4)
式中,w1、w2为用户节点U1与U2上的零均值、单位方差加性白高斯噪声。由于U1与U2已知所有链路的估计信道,根据已知的信息,通过自干扰消除可得到
(5)
式中,等式右边第一项为所接收的信号,第二项和第三项为噪声。
3 模型性能分析
3.1 平均信道容量分析
根据式(5)可以得到n个中继节点参与转发时端到端的接收信噪比为
(6)
式中,γu1、γu2分别为用户U1与U2接收信噪比。由此,可得在多中继节点下,采用AF机制的无线双向中继网络的平均信道容量为
(7)
式中的1/2是由于一次信息传输占用了两个时隙产生的,假设信道为具有对称性的高斯白噪声信道,即对任意中继节点有|hi|=|gi|=1,且令pi=pr,pr则表示中继节点的发射功率。上式可进一步简化为
(8)
3.2 中断概率分析
对于双向协同通信系统中的两个用户节点U1与U2来说,当能够达到的传输速率小于目标传输速率时,节点即发生中断;对于整个双向中继系统而言,双向协同通信系统可以等效为一个多用户的系统,当系统中任意用户节点发生中断,即可认为发生了系统中断事件[11]。因此,基于双向多中继AF协同方案的系统中断概率可以表示为
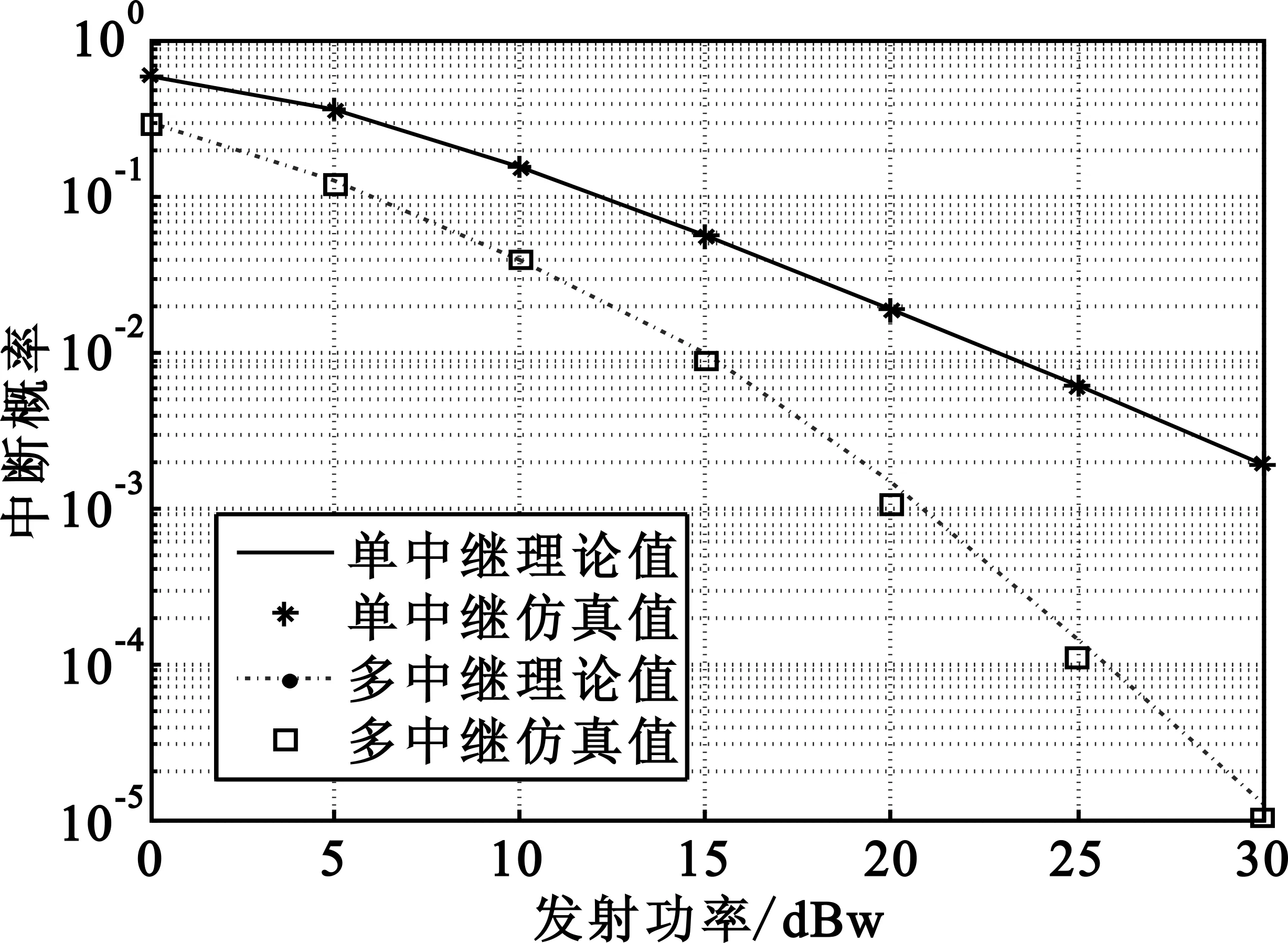
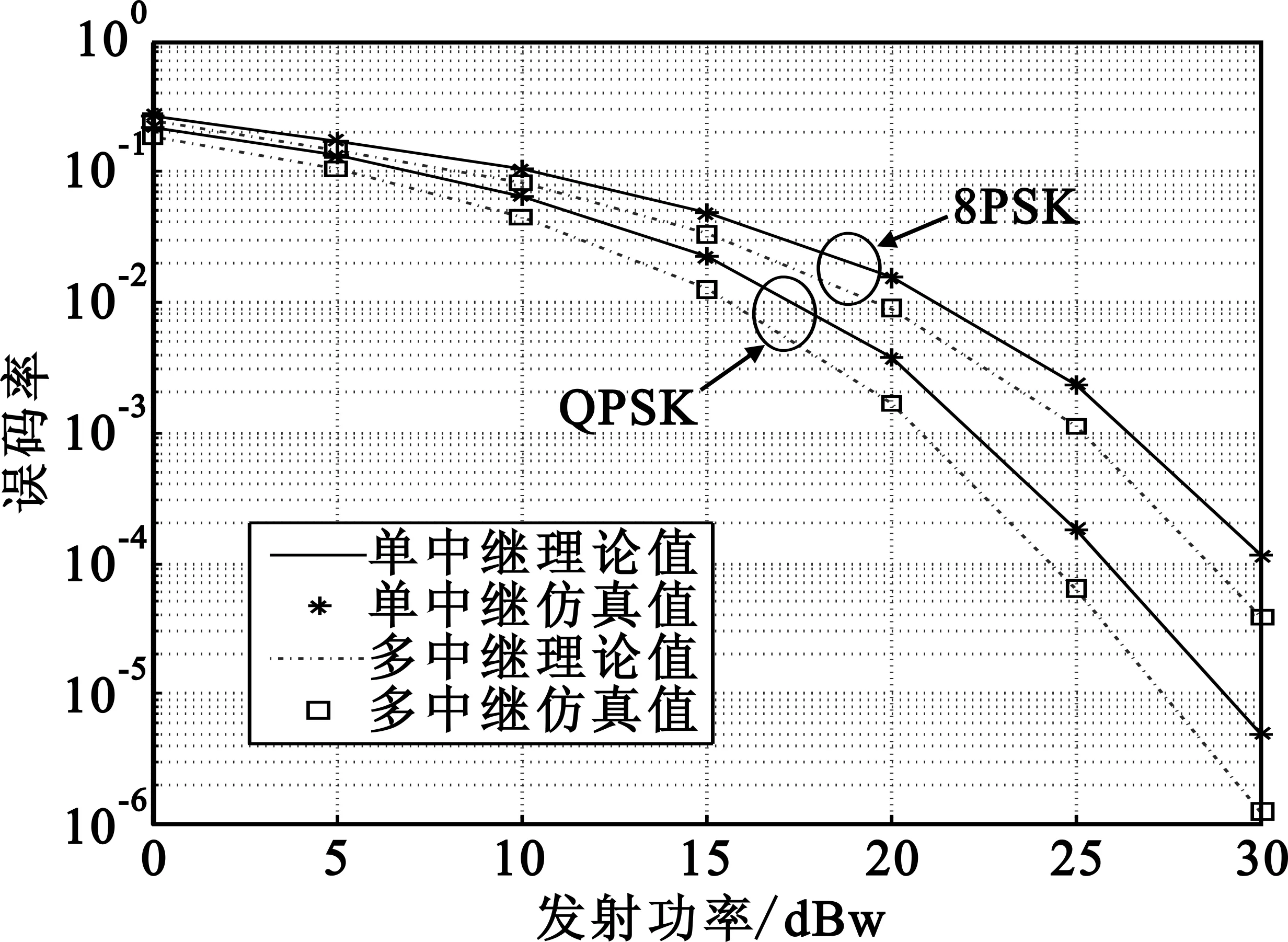
Pout=Pr(R21 Pr(γu1<γorγu2<γ) (9) 式中,r为系统的目标传输速率,γ=22r-1为目标信噪比。对上式进行求解,首先要知道γu1和γu2的概率累积分布函数(Cumulative Distribution Function,CDF)。因系统含有多个中继节点,要得到其闭合累积分布函数非常困难[12]。因此,可以通过推导中断概率的闭合上界进行估计,即 (10) 通过该式可以求得系统至少能达到的中断性能。式中Pi为以单独Ri节点为中继时双向链路的中断概率,其值可以表示为 Pi=Pr(R21,i Pr(R21,i Pr(γu1,i<γ)+Pr(γu2,i<γ)- Pr(γu1,i (11) 上式表示以Ri节点为中继的单条双向链路的中断概率情况,式中Pr(γu1,i<γ)为节点U1接收信号的中断概率,Pr(γu2,i<γ)为节点U2接收信号的中断概率,Pr(γu1,i 由于本文研究的所有信道都为频率非选择性瑞利衰落信道,信道增益gi和hi都为独立的复高斯随机变量,所以gi~CN(0,σgi),hi~CN(0,σhi)。据此可得:|gi|2和|hi|2分别服从参数为λi=1/σgi以及θi=1/σhi的指数分布。为简化推导,假设所有中继节点的功率pi与用户节点的发射功率相同且均记为p,则以单个节点Ri为中继时,用户U1接收信号的中断概率可表示为 Pr(γu1,i<γ)= (12) 其中,K1(·)为第二类一阶修正贝塞尔函数。同理可得单个节点Ri为中继时,用户U2接收信号的中断概率 (13) 单个节点Ri为中继时,双向链路同时中断的概率为 Pr(γu1,i (14) 且 分别将式(12)~(14)代入到式(11)中就可求得Pi的值,将其代入到式(10)中就可求出多中继双向协同通信系统中断概率的闭合上界。 由于系统在用户节点U1与U2处的译码相互独立,所以可以定义系统的平均误码率为 (15) 从上式可以看出系统的平均误码率是两用户接收信噪比的函数。当一个用户的接收信噪比取得最大值时,另一个用户的接收信噪比至少是一个较大值[13],因此可得如下近似: γu≈max(γu1,γu2)≈γu1≈γu2 (16) 通过以上两式可得Pser≈Pser(γu),根据公式(10)的定义,可知Pser(γu)的概率密度函数可表示为 (17) 式中,f(γi)和F(γi)分别表示γi的概率密度函数和累积分布函数。 由文献[9]可知,随机变量γu在高信噪比条件下的矩母函数近似为 (18) 仍假设所有中继节点的功率pi与用户节点的发射功率相同并均为p,式中,ηi=(pσgiσhi)/2(σgi+σhi),ak=0或1,k=1,2,…,n。 本文主要对MPSK信号的误码率进行研究,其平均误码率由下式表示: (19) 将式(18)代入到上式可得 (20) 上式中的积分可以通过文献[13]中如下公式求得其闭式解: (21) 然后,经过代数运算之后就能够得到如下的MPSK信号的误码率表达式: (22) 式中,Tj的表达式如下: (23) 为了证明双向多中继方案的优越性,本节将给出具体的数值仿真结果来分析和比较多中继与单中继双向协同通信系统的中断性能及平均误码率,验证理论分析的正确性,并对中继数量不同情况下误码率性能的变化进行仿真分析。在仿真中,不失通信条件的一般性,可将噪声方差设置为1,所有信道都为瑞利平坦衰落信道。因而,模型中网络节点的发送功率与信噪比的数值相同。将目标传输速率设为R=0.5 b/s·Hz-1。 中断概率的仿真结果如图2所示,以QPSK调制为例,在系统发射功率为0~30 dBw的情况下,对比了单中继模型和4个中继的多中继模型的中断概率。从图中可以看出双向多中继协同通信系统的中断概率性能明显优于单中继系统,并且随着发射功率不断增大优势更加显著,当发射功率为30 dBw时,多中继系统的中断概率性能提高了两个数量级。仿真曲线与理论值之间只有一点细微差别,说明了双向多中继中断概率理论上界分析的正确性。 图2 不同发射功率情况下的系统中断概率Fig.2 The outage probability versus transmit power 图3为QPSK和8PSK调制方式下误码率性能的解析结果和仿真结果,图中多中继模型的中继数目仍为4个。误码率的解析表达式是在高信噪比下的近似,但是它在整个信噪比范围内都与仿真结果吻合得很好,验证了平均误码率理论分析的正确性。从图中还可以看出多中继模型的平均误码率低于单中继模型,说明了双向多中继协同通信系统误码率性能的优势。 图3 不同发射功率情况下的系统平均误码率Fig.3 The SER performance versus transmit power 图4针对中继节点数目从1到10,在QPSK和8PSK调制方式下,发送功率为20 W时,对系统的误码率性能进行了仿真。 图4 不同中继个数情况下的系统平均误码率Fig.4 The SER performance versus the number of relays 从图中可以看出,QPSK调制方式的误码率性能在各种中继个数条件下都优于8PSK调制方式,随着中继个数的增加,多中继的分集增益更加明显,两种调制方式下系统的误码率都不断降低。但在实际应用中,由于通信设备的复杂度有一定限制,中继节点的个数并不能无限制地增加,所以应根据通信环境对大量的节点进行中继选择,在满足通信指标的前提下,尽量减少中继节点数目。 本文主要研究了双向多中继协同通信系统的理论性能。在频率非选择性瑞利衰落信道条件下,首先基于模型的放大转发传输机制,分析了系统的信道容量。在此基础上,推导了系统的中断概率,得到了中断概率的闭合上界表达式;进一步在MPSK调制方式下,推导了平均误码率的闭合表达式;最后对多中继模型的中断概率和平均误码率两项指标进行了仿真,并与单中继模型进行比较。仿真结果说明了多中继模型在中断概率和平均误码率两方面性能指标都优于单中继模型,并且验证了理论推导的正确性。本文在理论上研究了双向多中继协同通信系统的性能,对于双向多中继协同通信系统的实际应用具有指导意义,未来将对多中继多天线协同通信系统的性能开展进一步研究。 [1] Rossetto F,Zorzi M.Mixing network coding and cooperation for reliable wireless communications[J].IEEE Wireless Communications,2011,18(1):15-21. [2] 袁苑.非再生协同通信系统分集性能分析[J].电讯技术,2009,49(9):45-48. YUAN Yuan.Diversity Performance Analysis of Nonregenerative Cooperative Transm ission Systems[J].Telecommunication Engineering,2009,49(9):45-48.(in Chinese) [3] Kim T T,Skoglund M,Caire G.Quantifying the loss of compress-forward relaying without wyner-ziv coding[J].IEEE Transactions on Information Theory,2009,55(4):1529-1533. [4] Rankov B,Wittneben A.Spectral efficient protocols for halfduplex fading relay channels[J].IEEE Journal on Selected Areas in Communications,2007,25(2):379-389. [5] Nam W,Chung S Y,Lee Y H.Capacity bounds for two-way relay channels[C]//Proceedings of 2008 IEEE International Zurich Seminar on Digital Object Identifier.Zurich,Switzerland,:IEEE,2008:144-147. [6] Chen J,Wen C.Near-Optimal relay subset selection for two-way amplify-and-forward MIMO relaying systems[J].IEEE Transactions on Wireless Communications,2011,10(1):37-42. [7] Havary N V,Shahbaz P S,Grami A.Optimal network beamforming for bi-directional relay networks[C]//Proceedings of 2009 IEEE ICASSP.Taipei,Taiwan:IEEE,2009:2277-2280. [8] Ji X D,Zheng B Y,Cai Y M,et al.On the study of half-duplex asymmetric two-way relay transmission using an amplify-and-forward relay[J]. IEEE Transactions on Vehicular Technology,2012,61(4):1649-1664. [9] Yang Y,Ge J H,Ji Y C,et al.Performance analysis and instantaneous power allocation for two-way opportunistic amplify-and-forward relaying[J].IET Communications,2011,5(10):1430-1439. [10] Atapattu S,Jing Yingdi,Jiang Hai,et al.Tellambura,Opportunistic relaying in two-way networks[C]//Proceediugs of 5th International ICST Conference on Communications and Networking in China.Beijing:IEEE,2010:1-8. [11] Zhang J,Bai B,Li Y.Outage-optimal opportunistic relaying for two-way amplify and forward relay channel[J].IEEE Electronic Letters,2010,46(8):595-597. [12] Gou H,Ge J H.Outage probability of two-way opportunistic amplify-and-forward relaying[J].IEEE Electronic Letters,2010,46(13):918-919. [13] Simon M K,Alouini M S.Digital Communication over Fading Channels[M].2nd ed.New York:Wiley,2005:126-128.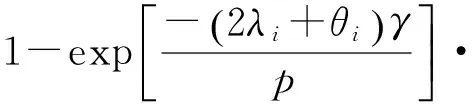
3.3 误码率性能分析
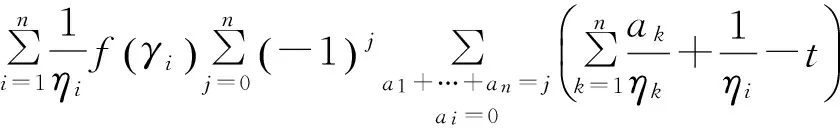

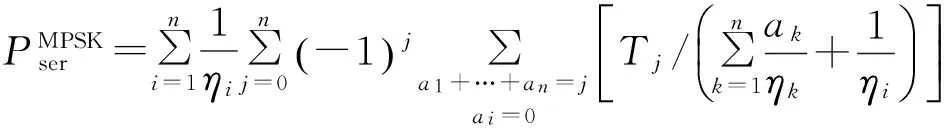
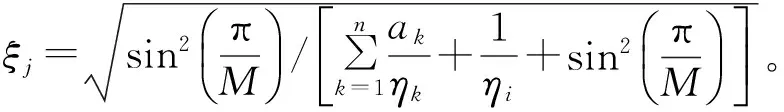
4 仿真分析

5 结 论
