解答数学题是干啥的？

2014-02-01江苏省睢宁高级中学南校吴少堂黄安成

中学数学杂志 2014年2期

关键词：数学题教者结论

☉江苏省睢宁高级中学南校吴少堂黄安成

解答数学题是干啥的？

☉江苏省睢宁高级中学南校吴少堂黄安成

我们都知道解答数学题是巩固知识、熟练技能、训练思维、发展智能、优化心理和磨砺意志的需要，归根到底是为了提高考试成绩、升入理想的大学.但本文从另一个视角来解读，则得到意料之外且新颖别致的答案，但究其实质，却又在情理之中.

一、解答数学题是游戏玩耍

将解答数学题的活动变为游戏玩耍，这是多么神奇美妙的一种境界！世界级的数学大师陈省身先生最著名的话语就是“数学好玩！”由此，解数学题就不再是一种“痛苦的折磨”，而是一种愉快的享受！当然与打篮球、下象棋一样，这种“玩”有时也不是一件十分轻松和顺利的事情，但由于“玩心太重”，困难与挫折也就不在话下了.

例1 求sin238°+sin282°-sin38°sin82°的值.

解析“：38°、82°”，何方“怪物”？何怪之有？38°+82°= 120°，那么38°、82°、60°就是一个三角形的三个内角，则可取△ABC，使∠A=38°，∠B=82°，则∠C=60°.由此想到余弦定理a2+b2-2abcosC=c2，再由正弦定理得4R2sin2A+ 4R2sin2B-2×4R2sinAsinB°cosC=4R2sin2C°，则得sin2A+ sin2B-2sinAsinB°cosC=sin2C.

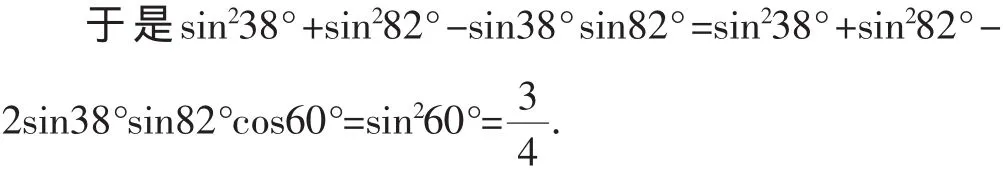
两个重要定理引领字母a、b、c与A、B、C以及一些数字做游戏，玩得可真算是智趣盎然、丰富多彩！

例2 已知a=（cosα，sinα），b=（cosβ，sinβ），0<β<α<π.

（2）设c=（0，1），若a+b=c，求α、β的值.

解析：字母、数字和运算都是我们的“玩具”，此外各种图形也是我们的“玩具”啊！此题是2013年某省的一道高考题，下面给出一种与公布的答案大相径庭且别开生面的解法.

（1）由已知得表示向量a与b的点A与B都在单位圆上（如图1）.

（2）又因为c=（0，1），表示单位圆上的点C（如图2）.

又a+b=c，所以AOBC构成∠A=60°的菱形，∠xOA= 150°，∠xOB=30°.

没用任何计算，两个非常熟悉的平面图形成了我们得心应手的“玩具”，想玩，会玩，运用与向量有关的“游戏规则”，可谓玩得绚丽多姿、赏心悦目.

二、解答数学题是刑侦破案

刑侦破案讲究四点，第一，获取的破案线索和有关信息很可能少得可怜，须扩大搜寻的范围；第二，获取的破案线索和有关信息虽然不少，但须经过精心辨析和筛选，去粗取精，去伪存真；第三，不可能一下子锁定作案人，开始时很可能只是怀疑对象，且怀疑的范围可能比较大，必须逐步缩小这个范围；第四，范围先扩大，后再缩小，当获取的线索和有关信息形成有力的证据链时，最终锁定犯罪嫌疑人，办成无懈可击的铁案.需要的是理性思维和悟性思维的密切配合.

现在的任务就是通过穿云破雾、抽丝剥茧，以确凿的证据锁定“嫌疑人”，以便将它“捉拿归案”.

首先由③得a5q+a5q2=3，结合②得q2+q-6=0.此关于q的方程有两个根，结合①知q=2.

因为n∈N+，所以1＜n≤12，所以n的最大值为12.

办案刑警为保一方平安，经常不辞劳苦、废寝忘食，甚至不顾生死地连续作战，大功告成后才倍感幸福.在这里我们当与他们感同身受了.

三、解答数学题是魔术揭秘

某些数学题的结构以及结论常显得匪夷所思和离奇古怪，真有些“魔幻”色彩.舞台上，魔术师的表演是不会将其中的奥秘告知观众的，故魔术表演被称为“掩盖真相的艺术”.揭露真相会使魔术失去悬疑性和观赏价值.可是数学题的解答与此却正相反，是完全彻底的“魔术揭秘”.

例4 水平地面上有一个篮球，它与地面唯一的接触点（即球与地平面的切点）为H（如图3），在斜平行光线的照射下，其阴影为一个椭圆.求证：H是椭圆的一个焦点.

解析：经斜平行光线的照射，球在地面上的阴影是椭圆形，很容易理解.可匪夷所思的是，这里的点H竟然是椭圆的一个焦点.这是命题者令人感叹的发现.发现也是一种创造嘛！我们能揭露其中的奥秘吗？

设球心为O（1作辅助线过程略），设椭圆的长半轴、短半轴、半焦距的长分别为a、b、c，球的半径为R，设椭圆的中心为O，那么在Rt△AO1B中，OA=OB=OO1=a，则要证的是OH=c.

戳穿谜底，原来如此简单.可魔术师坚守秘密是行规，数学教师揭示秘密也是行规啊！

解析：告诉你们，也许你们不信，已知函数式竟能化为cosθ-sinθ，“毛毛虫”蜕变为“花蝴蝶”，是什么“魔法”使然？现在就来揭穿其中的奥秘.

可能会有人质疑，这种“戏法”也太特殊了，能算通法吗？三角代换法算不算通法？算.凡变量a2+b2=1，则都可以设a=cosθ，b=sinθ；凡变量t∈［-1，1］，则都可以根据需要设t=cosθ，或t=sinθ；凡t∈R，则都可以设t=tanθ.不过这里有点小变化，设的是x+1=tanθ，为什么？图方便嘛！看似特技，实为通法.揭穿谜底，决不可怕！

四、解答数学题是观赏景致

数学是充满美的科学，我们则要努力既是景致的创造者，又是景致的观赏者，观赏自己辛勤加智慧的劳动成果，心理更加踏实和幸福.许多数学题目的多种解法，就给人以瑰丽多姿、流光溢彩的心理感受.特别地，当多种解法各具特色、风格迥然时，则除了观赏价值外，还具有“方寸天地，气象万千.一举多得，收获一片”的功效.

例6 △ABC的内角A、B、C所对的边a，b，c成等差数列，且A-C=90°.

解析：题目的已知条件非常“朴素”、“貌不惊人”：a，b，c成等差数列，且A-C=90°！可是欲证的结论却奇特异常，竟与无理数“”发生“亲缘”关系，想破脑袋也不会想到这样的结果！但此结论不仅不容置疑，且我们发现了六种不同的思路，限于篇幅和时间，这里仅给出其中的四种.

思路1：由已知，必有a＞b＞c，则可设a=b+d，c=b-d（0＜d＜b）.

最容易想到的就是此思路，不过计算比较麻烦些.但若掌握有关技巧则可减少麻烦.如将cosC的表达式中的“d”换成“-d”就得cosA的表达式；在得到关于d的方程后，在动手解题之前就可判断此方程必有解d=■ 7b，则给这个四次方程的解答带来很大的方便.

不须动笔，即知此方程必有解为d=1.岂不精妙至极！

有了三边的关系，如何证得结论，这里就不赘了.

仅有四十几个字符的短题，解起来竟涉及众多知识、技能、技巧和思想方法，对丰富大脑营养的补给和思维的启迪，收获太丰硕了，且精湛景致的创造和欣赏在心灵中将留下美好而深刻的记忆.

五、解答数学题是科研探索

虽然中学生离真正意义上的科研探索还很遥远，但我们在教学中可以且应该大力提倡探究式的学习方式，努力引领学生在问题解决中逐步学会运用数学探索的手段和方法，走进数学科研的门槛，初步品尝数学科研的滋味，感受获得成果的喜悦，启发向科学进军的决心和动力，为将来从事真正意义上的科研探索打下知识、技能、思维、心理和意志品质的基础.

例7 在平面直角坐标系xOy中，若已知A（x1，y1）、B（x2，y2）、C（x3，y3），你能求出△ABC的面积S吗？请将这个问题作为数学科研课题，写出小论文.

三角形的三个顶点的坐标确定，其面积肯定确定，问题是如何建立面积S与六个字母之间的内在联系.学生在以往解题时已获得了初步经验，即先从简单的特殊情况入手，然后再将问题一般化，最后力争将结论简单化，既重视此结果，更享受其过程，并总结进行数学科研探索的心得与体会.

解析：先研究一种特殊情况，即C与原点O重合（如图5）.

再研究一般的情况，尽可能应用上面已获得的成果.

学生回顾科研探索的过程时，感慨万千，他们表示：虽然这个结论也许早已存在，但对于我们来说却是第一次接触，所以仍具有研究的突破性（教者插话：你们今后将会取得更大的实质性的突破）；要不是先来个特殊化，这个问题根本就解决不了（教者插话：能解决，但麻烦太大了.先特殊后一般是数学研究，也几乎是所有科学研究的规律）；当得到cosθ的表达式后，欲想求sinθ的表达式，心里开始也有过动摇，后来坚定了决心，才执著地坚持了下去，没想到代入面积公式后，经过约简，竟得到一个非常简洁的公式①（教者插话：若不坚持，又怎能从奇妙的过程中享受到无比的乐趣.公式①简单的显示是数学的简洁美，越简单的结论，越有实用价值，越具有生命力.虽然公式②不算很简单，但后来人们创造了一个数学工具，可以迅速记住并掌握这个公式，不过现在还不能告诉你们）；整个探索过程具有一定的创造性，但不能否认扎实的基础知识和技能的重要作用（教者插话：夯实基础与思维灵活两者不可偏废，且相得益彰）；此问题当然不可能成为高考试题，但具备了这种探索科研能力，以后在考场上遇到从未见过的试题，也能做到处变不惊、临危不乱，最终实现克“题”制胜（教者插话：从现在起就打下探索科研的深厚扎实基础，将受益终生）.

六、解答数学题是工程建筑

随着国家建设的飞速发展和日新月异，各种工程建筑纷纷上马.面对这些工程，我们常在想，解答数学题不也是在搞“工程建筑”吗？特别是一些中、大型综合题的解答，更需要经过“勘探、设计、施工、监督、完工、验收”等基本程序，有时候还要进行“定期回访”和“跟踪服务”.工程中还有数不清的各种管道和线路，既需要整体的宏观设计，又需要精心的细微加工.遇到关键“节点”，还要想方设法予以即时和恰当的处置.

例8 设函数（fx）=x4-2ax2，已知当x∈［0，1］时，关于x的不等式＞1的解集为空集，求满足条件的实数a取值的集合.

解析：勘探：（fx）是四次函数，f（′x）是其导函数，求满足条件“…”的实数a取值的集合.