重视直观，学会抽象——以一道三角函数对称性习题拓展学习设计为例

☉湖南省株洲县第五中学 罗 灿

重视直观，学会抽象
——以一道三角函数对称性习题拓展学习设计为例

☉湖南省株洲县第五中学 罗 灿

一、问题提出

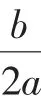
二、对一道三角函数对称性习题的拓展学习设计

1.习题呈现与分析

教材必修4第46页习题1.4A组第11题：

容易知道，正弦函数y=sinx是奇函数，正弦曲线关于原点对称，即原点是正弦曲线的对称中心.除原点外，正弦曲线还有其他对称中心吗？如果有，对称中心的坐标是什么？另外，正弦曲线是轴对称图形吗？如果是，对称轴的方程是什么？

你能用已经学过的正弦函数性质解释上述现象吗？

对余弦函数和正切函数，讨论上述同样的问题.

分析：该题的主要意图，是引导学生对三角函数的对称性有一个完整的认识.教师用书说明“利用三角函数的图象和周期性研究其对称性.”要顺利实现该习题讨论，理顺下列思考：

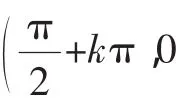
（2）如何多角度发现、描述对称性？譬如，单位圆也可提供“形”的支持；诱导公式提供“数”的支持；当然，周期性、奇偶性既可提供思考的类别参考，也与对称性本身存在内在的联系.

（3）将得到的三角函数的对称性进行运用上的迁移.直接的运用是正弦型函数、余弦型函数和正切型函数的对称性.

（4）学习形式化的表达对称性，即用符号语言表述轴对称和中心对称.尝试用对称的符号语言证明对称问题、对称产生周期的推导.

（5）如何保证教学组织的有序、有效？问题串、学生数学活动、教师示范等有机组合需要精心设计.

2.教学设计

活动1：探讨正弦函数y=sinx图象的对称中心.

问题串：

（1）作出正弦函数y=sinx的图象，除了原点外，你还能找到其他对称中心吗？它们之间有什么联系？能统一表示吗？

设计意图：借助图象，观察正弦曲线对称中心的不唯一性、几何特征及代数表示.

（2）将直角坐标系“抽掉”，只剩下正弦曲线，若将正弦曲线比喻为不断的从波谷→波峰→波谷……的爬坡下坡过程，你能找到对称中心的位置吗？

设计意图：帮助学生意识到对称性是“图”固有的几何属性，没坐标系，有好多“对称中心”都可能作为原点，坐标系的“加入”改变的只是坐标外在“模样”.将正弦曲线比喻为不断的爬坡下坡，那么对称中心正好处在“半山腰”.

（3）对于正弦曲线“上坡路”的“半山腰点”是对称中心，你可以从正弦函数的那条性质给出解释？怎么解释正弦曲线“下坡路”的“半山腰点”（譬如点（π，0））也是对称中心？

设计意图：前者主要是周期性；后者可调整观察视角：从右往左看，或者将原正弦曲线上下“翻个身”，则下坡变上坡，问题变为已解决问题.这里不变的是原图形中的对称性.

活动2：探讨正弦函数y=sinx图象的轴对称.

（4）观察正弦曲线，它是轴对称图形吗？如果是，对称轴的方程是什么？

设计意图：通过观察直接发现正弦曲线也是轴对称图形.

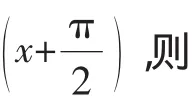
活动3：探讨函数y=f（x）关于直线x=a（点（a，0））对称形式化描述.

（6）偶函数关于直线x=0对称用符号表示为f（-x）=

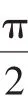
设计意图：是学生经历特殊到一般、具体到抽象、图象到符号的思维过程对函数的轴对称给出形式化定义，即y=f（x）关于直线x=a对称⇔f（a-x）=f（a+x）⇔f（2a-x）=f（x）.

（7）奇函数关于原点（0，0）对称用符号表示为f（-x）=-（fx），类似地，对正弦函数y=sinx关于点（kπ，0）（k∈Z）对称如何用符号表示？一般的，对函数y=f（x）关于点（a，0）对称如何给出形式化描述（定义）.

设计意图：同问题6，y=f（x）关于点（a，0）对称⇔f（a-x）=-f（a+x）⇔f（2a-x）=-f（x）.

活动4：探讨余弦函数的对称性.

（8）观察余弦曲线，说出其对称中心和对称轴方程，并用对称定义验证.

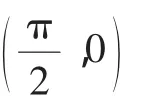
活动5：探讨正切函数的对称性.

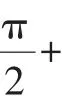
活动6：探讨对称性产生周期.

（10）观察正弦函数y=sinx图象，相邻两条对称轴的距离、相邻两个对称中心的距离、相邻一条对称轴和一个对称中心的距离，它们与正弦函数的最小正周期T=2π存在什么关系？

设计意图：以正弦函数为模型，从直观入手，发现对称性的三种“组合”产生周期这一事实，为猜想和推广提供直观模型支持.

（11）将问题10推广：对于函数y=f（x）：2（a-b）；

②若有两个对称中心（a，0），（b，0），则周期T=2（ab）；

③若有一条对称轴x=a和一个对称中心（b，0），则周期T=4（a-b）.

设计意图：揭示函数对称性和周期性二者间的内在联系，进一步熟悉数学形式化语言的表述，为学会“抽象”积累活动经验.教师可示范其中一个的推导，余下供学生练习.

三、两点感想

1.重视直观、学会抽象

“普通高中数学课程标准（实验）”有一条课程基本理念是“强调本质，注意适度形式化”.对此讨论的文章比较多，“本质”到底是什么，谁说了算？有时是比较模糊的；另一种倾向，过分强调直观而停留于直观层面的教学为数不少，这实质上有悖于课程理念初衷.课标的完整表述是“形式化是数学的基本特征之一.在数学教学中，学习形式化的表达是一项基本要求，但是不能只限于形式化的表达，要强调对数学本质的认识，否则会将生动活泼的数学思维活动淹没在形式化的海洋里.”从中可看出，“形式化”是“基本特征”“基本要求”，试问，谁能堪当“基本”？高中生的思维发展和心理发展应该是到了较高层次，对适度的形式化学习是能接受的.张奠宙先生在文［1］指出那种“要求高中教学比小学教学多多游戏、进行戏剧扮演的教学方式，恐怕是有悖常理的.”数学家徐利治将其一生数学学习、科研经验心得概括为六句话：培养兴趣、追求简易、重视直观、学会抽象、不怕计算、喜爱文学.笔者很喜欢徐老的“六句箴言”，本文的立意，就取乎徐老的三、四两句，笔者以为，高中数学学习，直观是起点、立足点，但还要学会抽象，通过抽象实现提高，将数学学习上升到更高层面，这才是用发展的眼光培养人，也才能适应今后的进一步学习.

2.观念引领、思想导航

在阅读文［3］过程中，从杨振宁大师身上笔者强烈感受了对称思想的魅力和力量.文［3］介绍杨先生在中学时代就对自然界的对称性产生了很强烈的感情，他的第一篇论文，就是关于物理学中的对称性问题.在他以后的科学生涯中，最重要的贡献也是在这个领域做出来的，他所写的二百余篇论文有三分之二是有关对称性问题的.1956年与李政道合作发表《弱相互作用中的宇称守恒问题》开创了对称思想发展的新纪元，杨先生把对称性在物理学中的核心地位与作用概括为一个基本原理：对称性支配相互作用原理.大师的理论博大精深，笔者万难领略皮毛一二，但对其精神感召却似有所悟：播下一些重要的思想观念种子，看似若隐无功，埋在心底，未尝不会待机萌发？难有大作为，小乐趣也别有风味，下举一例：

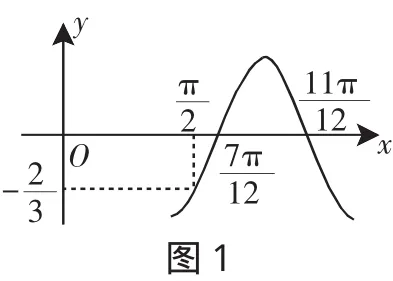
1.张奠宙.“非传统教学方式”要适合学生的年龄［J］.数学教学，2011（5）.

2.章建跃.数学4（必修）［M］.北京：人民教育出版社，2012.

3.高策.走在时代前面的科学家——杨振宁［M］.太原：山西科学技术出版社，1999.

4.罗灿，方厚良.追求知识与思想交融并行的数学学习［J］.数学通讯，2013（5）.