“成果扩大”：解题教学的一种追求——由一次习题讲评课说起<br/>

“成果扩大”：解题教学的一种追求——由一次习题讲评课说起

2014-02-01广东省博罗县福田中学刘伯勋

中学数学杂志 2014年2期

关键词：外角平分线一题

☉广东省博罗县福田中学刘伯勋

“成果扩大”：解题教学的一种追求
——由一次习题讲评课说起

☉广东省博罗县福田中学刘伯勋

解题教学在初中数学教学中占有十分重要的位置，追求解题教学的效益最大化，一直是广大教师心中向往的目标.本文从一次习题课的教学片断说起，阐释在解题教学中对“成果扩大”的追求和思考.

一、一次习题课的教学片断

以下是七年级学习三角形内角和及推论后一次习题课上的教学片断.

例1 如图1，在△ABC中，CP平分∠ACB，BP是△ABC的外角∠ABE的平分线，

试分析∠P与∠A的大小关系.

不少同学都感到很惊讶.

师：你是怎么发现的？

这样一说，部分同学表示能听懂，但还是有些学生感觉云里雾里，表示不是很清楚，于是在笔者帮助下，把生1表达的过程重新板书如下.

由△BCP外角的性质，得到∠P=∠PBE-∠PCB.

由△ABC外角的性质，得到∠A=∠ABE-∠ACB.

这样一来，更多的同学懂了.

师：同学们，现在老师再把问题变式如下.

变式1：如图2，在△ABC中，∠B、∠C的平分线交于O点，探究∠BOC与∠A的关系.

师：你怎么这么熟练？

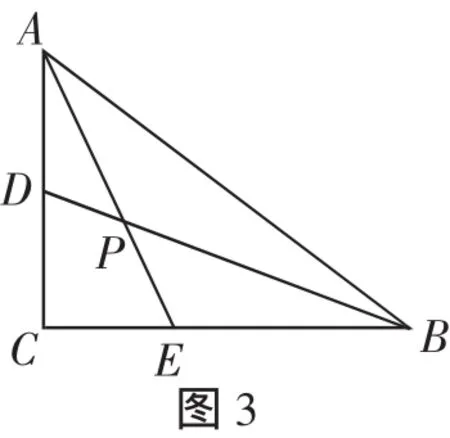
生2：我以前练习过这样一类问题：如图3，在Rt△ABC中，∠ACB＝90°，AE、BD是∠A、∠B的平分线，求∠APB的度数.

师：很好，你刚才的解题经验中，说出了一种重要的求解策略，即从特殊到一般的发现、归纳法，而且积累了一种特殊图形及其性质.现在让我们再“从内到外”，探究一下三角形两个外角平分线的夹角有怎样的性质.

变式2：如图4，在△ABC中，BP、CP分别是△ABC的外角∠DBC、∠ECB的平分线，试求∠BPC与∠A的大小关系.

学生经过2分钟的独立思考.

师：正确！原来三角形的两个角平分线的夹角与“第三个角”都存在一种规律！我们在前面曾说三角形的三条内角平分线会交于一点，属于一种数学上的奇异美现象，我想，上面三种“两角平分线”夹角的规律也是一种奇异美吧！

二、解题教学应该追求“成果扩大”

解题教学中追求“成果扩大”能帮助学生“举一反三”、“做一题，会一类，通一片”，就“眼前利益”来看，能帮助学生提高解题能力、应试能力.此外，追求并传递“成果扩大”，正是践行下述观点的体现，波利亚在名著《怎样解题》中说“一个好的教师应该懂得并且传授给学生下述看法：没有任何问题是可以解决得十全十美的，总剩下些工作要做.经过充分的探讨与钻研，我们能够改进这个解答，而且在任何情况下，我们总能提高自己对这个解答的理解水平”.以下即围绕解题教学中追求“成果扩大”阐释相关思考.

1.“成果扩大”的前提是教学预设

凡事预则立，不预则废.追求“成果扩大”的解题教学，首先要做的是充分的教学预设.若教者对待教数学问题还未有充分思考、预设，那么在解题教学时过分期待“成果扩大”的精彩生成往往会落空.上述案例中，教师能在学生获得一种发现后，及时给出不同变式，促成“成果扩大”，显然这些变式的即时出现，其实在于教师在上课之前对这类问题（三角形“两角平分线”夹角问题）已了然于胸，预设之功显现于此.此外，由于“成果扩大”内涵和外延非常丰富，教学预设就显得更为重要.以下即展开说明对解题教学中追求“成果扩大”的更多认识.

2.“成果扩大”的本质是变式教学

我们知道，变式教学是有中国特点的“双基”特色.本文倡导在解题教学中追求“成果扩大”，本质上就是倡导变式教学.而变式教学的目的在于帮助和促进学生发现、积累模式，并善于对模式进行变式理解.在上述教学片断中，当学生经历变式与探究后，积累了三角形“两个角平分线”夹角的规律问题，这其实是陕西师大罗增儒教授倡导的“模式识别”策略，上述的探究和小结其实就是发现和积累模式图形与性质（也有资料上称“基本图形及性质”），这样在此后的作业或考试中，面对这类模式图形就可以快速打开思路，实现问题的快速突破.实际上，在平时的学习中，这样的变式探究及一般性规律的发现是十分重要的，只有多进行这样的一题多变的训练和反思，才能走出题海，更本质地学习知识，提高数学解题能力！

3.“成果扩大”的追求是回顾反思

我们知道，数学解题并不仅仅是追求答案的获取，还需要在“求出解答后继续前进”（舍费尔德语）.在这里，简单提及新加坡著名数学家、数学教育家李秉彝先生关于“答案、过程、表达”三者关系的论述：“首先，为什么答案是重要的？假如你在造一栋住宅，竣工后，房子塌了，你愿意因为仅仅是过程正确而向建筑商支付报酬吗？其次，为什么过程是重要的？你可以在过程做错的情况下，得到正确的答案，但我不肯定你下次还会那么幸运.第三，为什么表达是重要的？如果你说得很好，你可以通过一扇门，我是说，你可以把所要表达的意思传递给门后的那个人，如果你写得很好，你至少可以通过三扇门，我是说，你可以把所要表达的意思传递给你老板的老板的老板.只有完美的表达才可以传递得更远.”这样来看，如上述案例所见，在学生获得例1的解答后，并没有结束该题的学习，而是连续变式两次，在师生的对话中丰富了这一类问题.进一步，还在点评环节，引导学生对比不同例、习题的求解，发现并感受结论的“奇异美”，这一系列的跟进措施都是“成果扩大”.

4.“成果扩大”需要处理与“必要优化”的关系

如上述案例展示所见，解题教学中的“成果扩大”追求了一题多变.此外，“一题多解”也是“成果扩大”的一种常见形式.无论是解题教学中的“一题多变”或“一题多解”，都要注意一个“度”.

首先，一题多变往哪个方向变？指向何方？这里不妨再链接笔者近期从教材上一道习题出发，预设的一道“五角星”（人教版八年级上册教材第82页第3题改编）的开放式问题.

例2 如图5，五角星的五个角都是顶角为36°的等腰三角形.

（1）填空∠AMB=_______°；

（2）连接AB，求∠MAB的度数；

（3）请过点M画出五角星的一条对称轴（尺规作图，保留作图痕迹）；

（4）请在（3）的图形上，再设计一个求角度的问题.

教学故事讲述：前两问是封闭式设问，后面增加的两问，就是让同学们看看，经典如五角星，还有怎样的设问方式.第三问在作对称轴时，虽然要求是尺规作图，不同的学生有不同的方法，有些认识很深刻的学生，直接连接两个点（点M和相对的“五角星”一个顶点）即可.而第四问学生设计的问题也丰富多样，其中一个学生设计一问：设∠A与∠B的平分线交于O，求∠AOB的度数.值得一说的是，这个问题的求解方法有很多，比如利用三角形内外角性质，或者走外接圆、圆心角的路径.可见一道精心预设的开放式问题，经过师生的共同努力，精彩生成，就有了很有价值的“成果扩大”.

其次，关于一题多解与解法优化的思考.如郑毓信教授所说，积极倡导解题方法的多样化与“思维的必要优化”，不应当看成是直接相冲突的.相反，很好的处理解法多样与思维的必要优化之间的辩证关系，正是教学艺术性的体现.这方面的一个有意义的思考，可以参见刘东升老师在《“通性通法”与“技巧解法”之思》一文中对解法多样的如下观点：恰当的解法多样化是应该坚持的问题解决取向、恰当的思辨有助于“通性通法”与“技巧解法”的理解、恰当的理解“技巧解法”与“特殊解题技巧”的关系.事实上，这也正是广大教师同行作为专业人士需要修炼的基本功之一——“善于优化”.