结合a分层的兼具项目曝光和广义测验重叠率控制的选题策略*
2014-01-31王卓然边玉芳
郭 磊 王卓然 王 丰 边玉芳,2
(1北京师范大学认知神经科学与学习国家重点实验室;2中国基础教育质量评价与提升协同创新中心, 北京 100875)
1 引言
计算机化自适应测验(Computerized Adaptive Testing, CAT)在过去几十年里备受关注, 已经成为了许多大规模教育测量项目的测验模式(陈平,2011)。与传统的纸笔测验相比, CAT的最大优势表现在测试更少项目的同时, 能够快速获取更加精确的能力估计值(Weiss, 1982), 并且施测更加灵活。由于近来年网络的快速发展, CAT的测验功效发挥到了极致, 像GRE、ASVAB、GMAT、美国护士资格考试等大型考试都采用了CAT (唐小娟, 丁树良,俞宗火, 2012)。
在CAT测验中, 特别是高风险(high stake)测验,考试的安全性十分重要(程小扬, 丁树良, 严深海,朱隆尹, 2011)。为了保证测验及题库安全性, 主要做法是控制题库中项目的曝光率, 使其低于预先设定的曝光率最大值。在CAT测验中, 研究者提出了许多控制项目曝光率的方法, 根据Georgiadou,Triantafillou和Economides (2007)的总结, 当前主要有5类项目曝光控制方法:(1)随机化方法; (2)条件选择方法; (3)分层方法; (4)结合前三者的综合方法; (5)多阶段自适应设计。然而, 以上的方法均只关注了项目曝光率的控制。
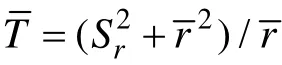
那么, 究竟该如何提高题库使用的均匀性呢?受Chang和Ying (1999)提出的a分层方法的启发,我们认为将a分层方法的思想和SHGT法相结合可以提高后者题库的使用率。a分层的优势在于, 能够提高未使用或较少使用项目的曝光率, 使得项目曝光率和题库使用率更加均衡。但根据Parshall,Harmes和Kromrey (2000)的研究表明, a分层对于某些项目仍然有较大的曝光率。并且在实际题库中,a与b通常都是正相关的(Lord, 1975), 如果某一层内难度b的范围不足以覆盖被试能力水平时, 将会导致某些项目过度选择。很明显, SHGT法和a分层法的缺陷可以相互弥补, 前者能够有效的控制过度曝光项目的出现, 但不能提高题库使用均匀性, 后者虽能提高题库使用率, 但未能有效地控制过度曝光的项目。因此, 本研究尝试将两种方法相结合,以实现既能控制项目曝光率和广义测验重叠率, 又能提高题库使用率的目的。
查阅国内外文献, 尚未见到能够在同时控制项目曝光率和广义测验重叠率的基础上, 提高题库使用率的研究, 并且没有研究过测验考察的内容比例对不同的选题策略有何影响。实际中, 不同测验所考察的内容比例是根据具体的测验目的而设置的,而题库的内容比例是相对稳定不变的。因此, 研究测验考察的内容比例对不同选题策略的影响很有必要。本研究将a分层、按b分块的a分层(Chang,Qian, & Ying, 2001)以及按内容分块的a分层方法(Yi & Chang, 2003)与SHGT法相结合, 分别记作SHGT_a法、SHGT_b法和SHGT_c法, 意在实现上述目标。本文拟采用蒙特卡洛方法进行模拟研究,意在探讨:(1)在不同的项目曝光率和广义测验重叠率水平下, 不同选题策略之间的表现有何差异; (2)在不同区分度和难度的相关水平下, 不同选题策略之间的表现有何差异; (3)在不同的内容考察比例下,不同选题策略之间的表现有何差异。
2 相关选题策略简介
2.1 SHGT法
SHGT法是一个比较复杂的选题策略, 它融合了SH法的思想, 同时控制了广义测验重叠率, 采用在线更新项目曝光控制参数的方法而成。该方法有几大优势:(1)可以同时控制项目曝光率和广义测验重叠率; (2)在线更新曝光控制参数, 无需迭代模拟, 大大节省了CAT的时间; (3)能够适用于题库中项目和被试群体发生变化的情况; (4)可以和其他选题策略相结合使用。
基于广义测验重叠率的概念, Chen (2010)给出了其计算公式:
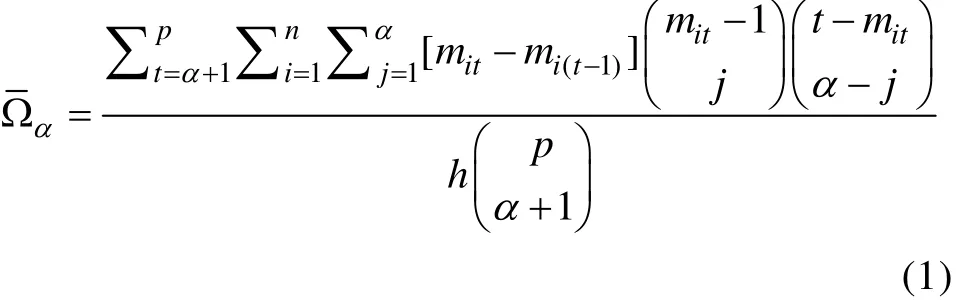

为了计算和编程的便捷性, 需要对广义测验重叠率进行重构, 可以根据递归算法进行计算,公式如下:
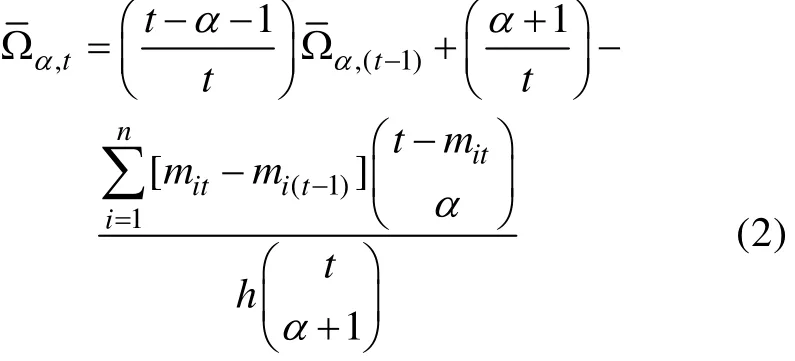
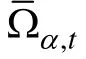
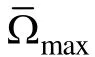
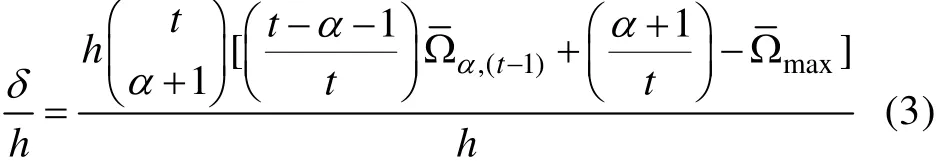
在定义了两个指标之后, SHGT法的具体操作分为以下几个步骤:
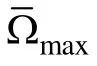
δ
/h
, 在给定的选题策略(在SHGT法中, 本文采用最大费歇信息量法; 在新方法中, 采用b-matching法)下, 若选出了题库中的第i题, 则将第i题的贡献率η
和临界值δ
/h
进行比较, 并且从均匀分布U
(0,1)中产生一个随机数x
。如果满足条件η
≥δ
/h
且x
≤k
, 那么施测第i题,否则将此题从题库中删除, 不再对该被试施测。如此往复;(3)在第一题i施测后, 将前一步的临界值δ
/h
更新为(δ
−η
)/(h
−1), 作为选择下一题比较的条件。将施测的第二题记作项目j, 当第二题j施测后,继续更新临界值为(δ
−η
−η
)/(h
−2), 即每做完一道项目就更新一次临界值, 如此往复;(4)基于已施测的t个被试的测验情况, 计算出每个项目的项目选择概率(记为P
(S
))和项目曝光概率(记为P
(A
)), 然后对k
值进行更新:如果P
(A
)>r
, 那么k
=0;如果P
(A
)≤r
并且P
(S
)>r
, 那么k
=r
/P
(S
);如果P
(A
)≤r
并且P
(S
)≤r
, 那么k
=1(5)更新完k
值后, 为了保证被试均能顺利完成CAT测验, 需要设置h个k
值等于1, 具体做法是令最接近1的那些k
值等于1, 直到有h个1为止;(6)在得到所有k
值后, 返回到第2步对第t+1个被试施测CAT测验。重复以上步骤直到所有被试参加完CAT测验。需要强调的是, 当设定的Ω趋近其下限值时, 会出现无题可选的情况, 此时应在步骤(2)后加上一个补救措施, 详细过程的描述请参见Chen(2010)。
2.2 a分层法, 按b分块的a分层法, 按内容分块的a分层法
2.2.1 a分层法 (STR_a)
Chang和Ying (1999)最早提出了a分层方法来提高题库安全性。经研究表明, 尽管高a的项目很有价值, 但当高a项目施测于能力真值与项目难度不接近的被试时, 该项目的价值并不能得到充分体现。当对被试能力真值认识有限时, 应尽量避免使用高a的项目, 并且在CAT早期阶段使用低a项目,后期使用高a项目的方式是合理的。由此, 他们提出了著名的a分层选题策略, 步骤为:(1)根据区分度a将题库分成K个水平; (2)相应地, 将测验也分成K个阶段; (3)在测验的第k个阶段, 选择项目难度与能力估计值最接近的h
个项目施测, 保证h
+h
+…+h
=h
; (4)重复步骤3。2.2.2 按b分块的a分层法(STR_b)
正如Chang和Ying (1999)的研究表明, a分层有较好表现的一个前提是a和b之间没有相关。但是在实际题库中, a与b通常都是正相关的(Lord,1975)。如果某一层内的b范围不足以覆盖被试能力水平时, 就会导致某些项目过度选择。而且在高a层中, 高a低b的项目很少, 将会导致这些项目过度曝光。于是, Chang, Qian和Ying (2001)提出按难度b分块的a分层法, 步骤为:(1)基于难度b将题库分成M块。所有组块中项目数量相同。将这些组块按照升序排列; (2)在每个组块中, 按照a值分成K个水平; (3)将同一水平的不同组块重新组合,形成K个水平的题库, 这样在同一水平内的难度b也覆盖了整个能力范围; (4)按照a分层的步骤进行CAT测验。若a和b的相关为0时, STR_b和STR_a是一样的。
2.2.3 按内容分块的a分层法(STR_c)
Van der Linden (2000)认为, CAT只有将统计性能和非统计要求相结合才能被接受, 即要在实际中考虑内容平衡等非统计属性, 以便CAT测验有较高的内容效度以及被试的测验分数可以比较。于是,Yi和Chang (2003)提出了按内容分块的a分层法,步骤为:(1)根据内容领域将题库分成若干个组; (2)在每个组里实施STR_b。若内容领域为一个时,STR_c和STR_b是一样的。
3 研究设计
本研究要比较的选题策略包括:随机选题法(RN)、SHGT法、SHGT_a法、SHGT_b法以及SHGT_c法。结合方式为, 首先运用STR_a (b或c)法将题库分层, 在每一层内使用SHGT法。其中,RN作为比较的基线。采用Matlab 2011b自编以上所有选题策略。
3.1 题库及被试
首先生成360题的题库(n
=360)。区分度a, 难度b以及猜测度c按如下先验分布生成:a
~U(0.5,1.5),b
~N(0,1), c~U(0,0.4)。其次, 本研究中固定题库所考察的内容领域数量g=3, 并且规定内容领域的项目数量比例为1:1:1, 各120题,由此生成模拟题库, 用于进行所有的实验。按照先验分布θ
~N
(0,1)生成3000名被试。3.2 实验条件及说明

本研究中CAT测验的终止规则选取定长CAT,这也是大多数CAT研究采取的方法。固定测验长度h=30, 这是因为Stocking (1994)建议题库大小至少应该是测验长度的12倍。若使用SHGT_a法, 令层数K=4。施测顺序为先施测低a层, 最后施测高a层。每层内项目数量固定为7题, 7题, 8题和8题; 若使用SHGT_b法, 令块数M=3, 再令层数K=4, 其他同SHGT_a法; 若使用SHGT_c法, 先按照内容领域将题库分成若干个组, 随后在每个组里实施SHGT_b法; 利用EAP法对被试能力进行更新。
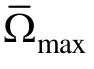
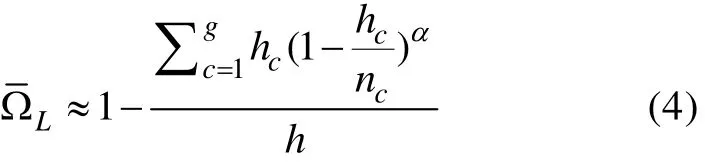
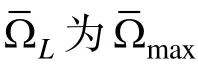
3.3 评价指标
(1)广义测验重叠率

(2)误差均方根
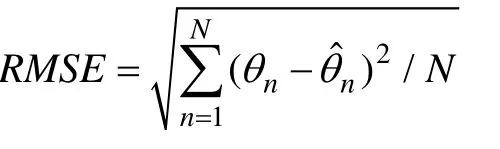
θ
和ˆθ
分别为能力真值和估计值。RMSE反映了参数真值与估计值之间的平均偏差大小, 其值越小越好。除此之外, 程序还记录了最大项目曝光率和使用过的项目数量, 以此考察各选题策略的性能。
4 研究结果
总体来看, 根据表1至表4的结果, 不论共享人数为多少, SHGT及3种新方法均能很好地控制项目曝光率和广义测验重叠率。例如, 根据表1结
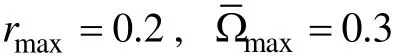

表1 rab=0.2, 测验内容比例为1:1:1时, 5种选题策略的结果

表2 rab=0.8, 测验内容比例为1:1:1时, 5种选题策略的结果
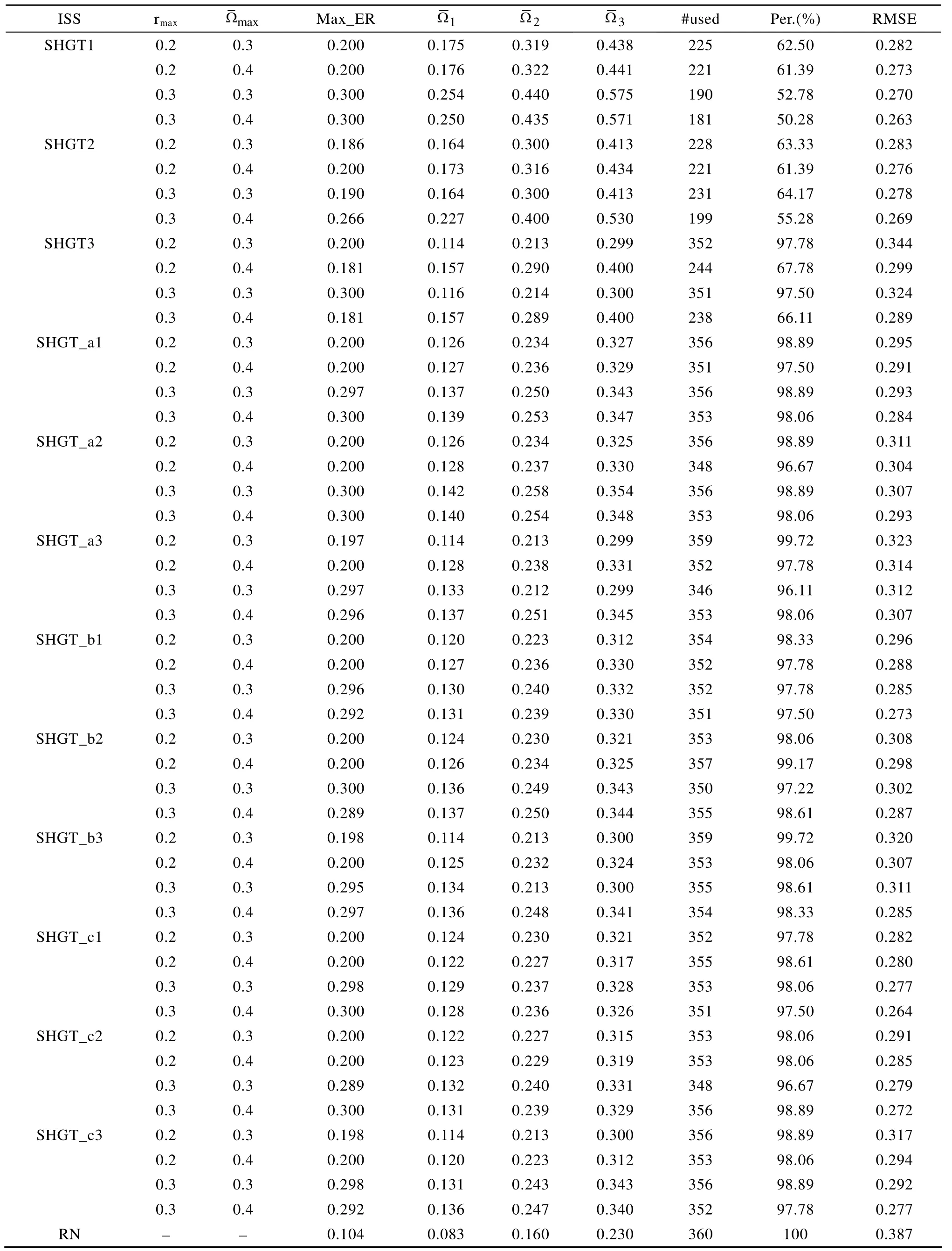
表3 rab=0.2, 测验内容比例为1:2:3时, 5种选题策略的结果
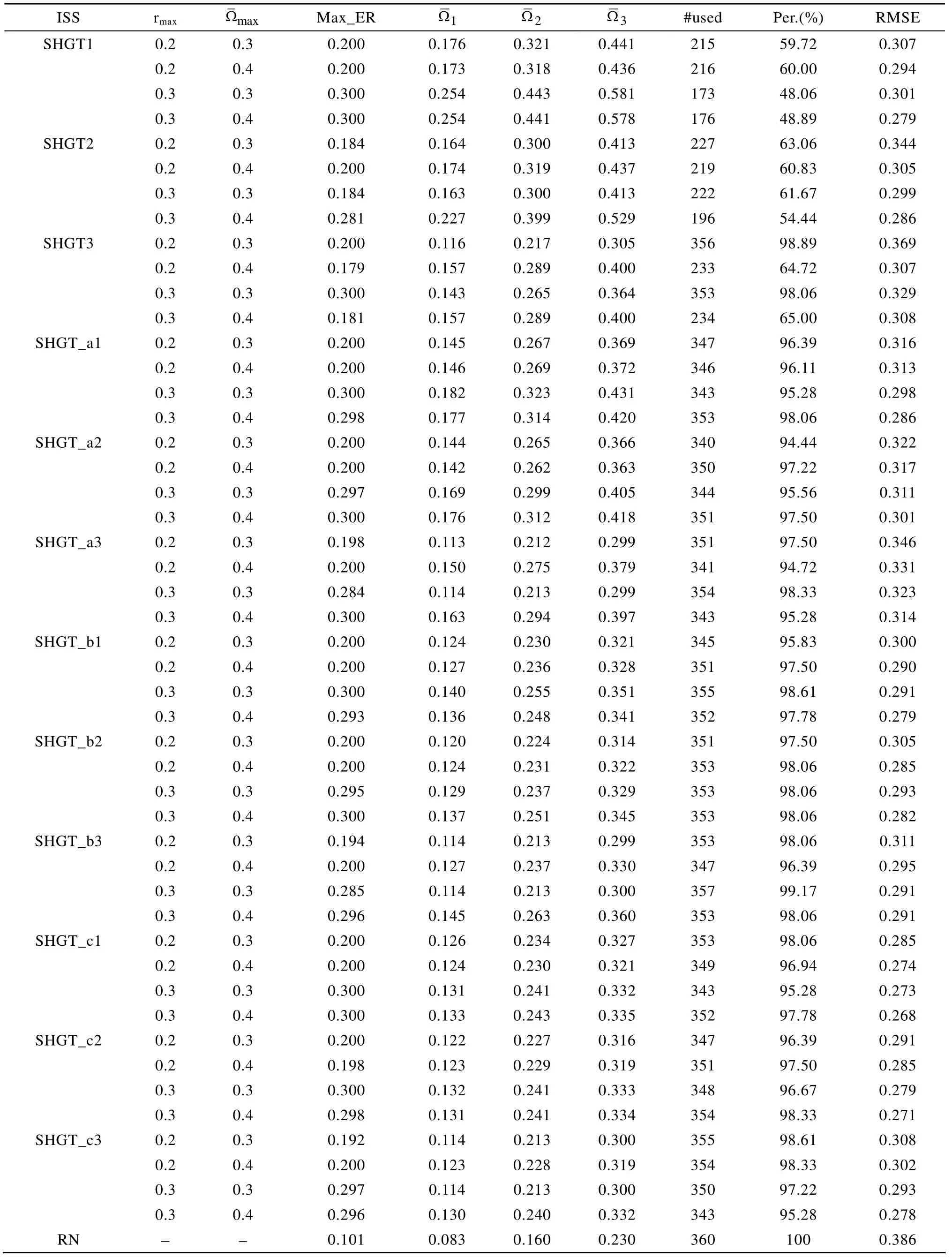
表4 rab=0.8, 测验内容比例为1:2:3时, 5种选题策略的结果


5 小结与讨论
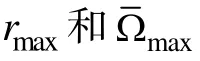
本研究借鉴a分层方法的思想, 成功地将SHGT法与不同形式的a分层法相结合, 在保留各自优势的前提下, 相互弥补了缺陷。SHGT法在控制广义测验重叠率的同时, 解决了项目过度曝光问题, a分层法可以有效提高题库使用率, 保证了测验安全性。
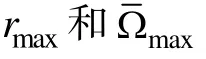
(1)本研究只采取了在a分层的每一层内选取近似相等的项目数量, 没有考察升序的实验条件。根据已有研究表明, 采用升序的a分层效果更佳(Chang & Ying, 1999; Chang & Ying, 1996, 2008; Hau& Chang, 2001), 这在以后研究中可以进行探讨;
(2)本研究发现, 在测验考察内容比例不均衡条件下, 新方法均有较稳定的表现, 尤以SHGT_c法表现最好。但这是在题库及内容数量相对较小,测验长度固定为30题时的结果。今后可以研究在不同题库容量、不同内容领域数量及比例条件下,新方法的表现;
(3) CAT的优势在于可以对每个被试的能力估计精度进行控制, 这时就需要采用变长的CAT。具体做法可以根据每层内达到的信息量值作为变长CAT的标准(Wen, Chang, & Hau, 2000; 戴海琦, 陈德枝, 丁树良, 邓太萍, 2006);
(4)程小扬等人(2011)提出了引入曝光因子的CAT选题策略, 该方法使题库中项目的调用更加均匀, 曝光率指标明显降低, 能力估计精度也较高。将该选题策略与本文提出的方法进行比较也是值得研究的方向。
Chang, H. H., Qian, J. H., & Ying, Z. L. (2001). A–Stratified multistage computerized adaptive testing with b blocking.Applied Psychological Measurement, 25
(4), 333–341.Chang, H. H., & Ying, Z. L. (1996). A global information approach to computerized adaptive testing.Applied Psychological Measurement, 20
(3), 213–229.Chang, H. H., & Ying, Z. L. (1999). A–stratified multistage computerized adaptive testing.Applied Psychological Measurement, 23
(3), 211–222.Chang, H. H., & Ying, Z. L. (2008). To weight or not to weight?Balancing influence of initial items in adaptive testing.Psychometrika, 73
(3), 441–450.Chang, H. H., & Zhang, J. M. (2002). Hypergeometric family and item overlap rates in computerized adaptive testing.Psychometrika, 67
(3), 387–398.Chen, P. (2011).Item replenishing cognitive diagnostic computerized adaptive testing—— based on DINA model.
Unpublished doctoral thesis, Beijing Normal University.[陈平. (2011).认知诊断计算机化自适应测验的项目增补—— 以DINA模型为例
. 博士学位论文, 北京师范大学.]Chen, S. Y. (2010). A procedure for controlling general test overlap in computerized adaptive testing.Applied Psychological Measurement, 34
(6), 393–409.Chen, S. Y., & Ankenman, R. D. (2004). Effects of practical constraints on item selection rules at the early stages of computerized adaptive testing.Journal of Educational Measurement, 41
(2), 149–174.Chen, S. Y., Ankenmann, R. D., & Spray, J. A. (2003). The relationship between item exposure and test overlap in computerized adaptive testing.Journal of Educational Measurement, 40
(2), 129–145.Chen, S. Y., & Lei, P. W. (2005). Controlling item exposure and test overlap in computerized adaptive testing.Applied Psychological Measurement, 29
(3), 204–217.Chen, S. Y., & Lei, P. W. (2010). Investigating the relationship between item exposure and test overlap: Item sharing and item pooling.British Journal of Mathematical and Statistical Psychology, 63
(1), 205–226.Chen, S. Y., Lei, P. W., & Liao, W. H. (2008). Controlling item exposure and test overlap on the fly in computerized adaptive testing.British Journal of Mathematical and Statistical Psychology, 61
(2), 471–492.Cheng, X. Y., Ding, S. L., Yan, S. H., & Zhu, L. Y. (2011).New item selection criteria of computerized adaptive testing with exposure–control factor.Acta Psychologica Sinica, 43
(2), 203–212.[程小扬, 丁树良, 严深海, 朱隆尹. (2011). 引入曝光因子的计算机化自适应测验选题策略.心理学报, 43
(2),203–212.]Dai, H. Q., Chen, D. Z., Ding, S. L., & Deng, T. P. (2006). The comparison among item selection strategies of CAT with multiple–choice items.Acta Psychologica Sinica, 38
(5),778–783.[戴海琦, 陈德枝, 丁树良, 邓太萍. (2006). 多级评分题计算机自适应测验选题策略比较.心理学报, 38
(5),778–783.]Georgiadou, E. G., Triantafillou, E., & Economides, A. A. (2007).A review of item exposure control strategies for computerized adaptive testing developed from 1983 to 2005.The Journal of Technology, Learning and Assessment, 5
(8), 4–37.Hau, K. T., & Chang, H. H. (2001). Item selection in computerized adaptive testing: Should more discriminating items be used first?Journal of Educational Measurement,38
(3), 249–266.Lord, F. M. (1975). The ‘ability’ scale in item characteristic curve theory.Psychometrika, 40
(2), 205–217.Parshall, C., Harmes, J. C., & Kromrey, J. D. (2000). Item exposure control in computer–adaptive testing: The use of freezing to augment stratification.Florida Journal of Educational Research, 40
(1), 28–52.Revuelta, J., & Ponsoda, V. (1998). A comparison of item exposure control methods in computerized adaptive testing.Journal of Educational Measurement, 35
(4), 311–327.Stocking, M. L. (1994).Three practical issues for modern adaptive testing item pools
(ETS Research Rep. No. 94–5).Princeton, NJ: Educational Testing Service.Stocking, M. L., & Swanson, L. (1993). A method for severely constrained item selection in adaptive testing.Applied Psychological Measurement, 17
(3), 277–292.Sympson, J. B., & Hetter, R. D. (1985).Controlling item–exposure rates in computerized adaptive testing.
Paper presented at the Proceedings of the 27th annual meeting of the Military Testing Association. San Diego.Tang, X. J., Ding, S. L., & Yu, Z. H. (2012). Application of computerized adaptive testing in cognitive diagnosis.Advances in Psychological Science, 20
(4), 616–626.[唐小娟, 丁树良, 俞宗火. (2012). 计算机化自适应测验在认知诊断中的应用.心理科学进展, 20
(4), 616–626.]van der Linden, W. J. (2000). Constrained adaptive testing with shadow tests. In W. J. van der Linden & C. A. W. Glas(Eds.).Computerized adaptive testing: Theory and practice
(pp. 27–52).
Norwell MA: Kluwer.van der Linden, W. J. (2003). Some alternatives to Sympson–Hetter item–exposure control in computerized adaptive testing.Journal of Educational and Behavioral Statistics, 28
(3), 249–265.Way, W. D. (1998). Protecting the integrity of computerized testing item pools.Educational Measurement: Issues and Practice, 17
(4), 17–27.Weiss, D. J. (1982). Improving measurement quality and efficiency with adaptive testing.Applied Psychological Measurement, 6
(4), 473–492.Weiss, D. J. (1985). Adaptive testing by computer.Journal of Consulting and Clinical Psychology, 53
(6), 774–789.Wen, J. B., Chang, H. H., & Hau, K. T. (2000).Adaptation of a–stratified method in variable length computerized adaptive testing.
Paper presented at the American Educational Research Association Annual Meeting. Seattle.Yi, Q., & Chang, H. H. (2003). a–Stratified CAT design with content blocking.British Journal of Mathematical and Statistical Psychology, 56
(2), 359–378.