△-∑小数分频频率合成器带外量化噪声滤除技术
2014-01-29胡礼扬
胡礼扬,王 军
(西南科技大学 信息工程学院,四川 绵阳 621010)
近几十年来随着通信、数字电视、卫星定位、导航技术的不断发展,对频率源的频率稳定度、频谱纯度、频率范围和输出频率个数的要求越来越高。为了提高频率稳定度,经常采用晶体振荡器等方法来解决,但它不能满足频率个数多的要求,因此,目前大量采用频率合成技术。小数分频频率合成器的相位噪声是通信系统最关键技术指标之一,例如GSM、分组无线业务、WCDMA等[1-2]。之所以采用高阶的delta-sigma调制器(DSM)小数分频频率合成器(以下简称频率合成器),因为它能提供很宽的带宽且分辨率高,并且可以在制约锁相环设计的一些因素,如相位噪声、锁定时间及参考杂散上折中选择等问题[3]。由于小数分频频率合成器可以产生一个小数分频比,这就使DSM不可避免的会有量化误差,而这种量化误差会产生高通量化噪声,从而使频率合成器输的相位误差就一步恶化[4]。因此有必要对高阶DSM的带外量化噪声进行抑制[5]。本文提出的噪声滤除技术就是要减少这种带外量化噪声,以及电荷泵(CP)引起的折叠噪声也可以得到抑制。在本文中提出的相位噪声滤除技术就是在频率合成器的反馈之路上添加一个锁相环(PLL),而这种锁相环可以视为带外量化噪声滤除器,这种噪声滤除器可以抑制由高阶DSM产生的带外量化噪声,并且减小由于PFD和CP非线性引起的折叠噪声。
1 △-∑调制器量化噪声
在通信系统中,小数分频频率合成器的相位噪声是关键的技术之一,如图1所示,为新型的小数分频频率合成器,在频域中,频率合成器的开环传输函数为
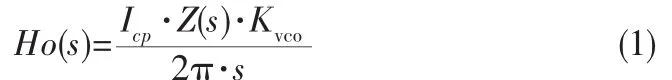
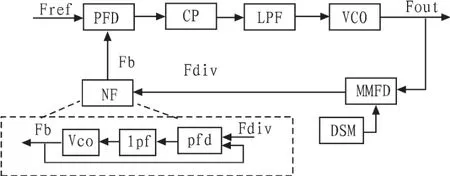
图1 小数频率合成器结构图Fig.1 Structure diagram of fractional-N frequency synthesizers
其中Kvco为压控振荡器(VCO)的增益,Z(s)为环路滤波器阻抗,Icp2π为PFD/CP增益,在此,设量化步长为1,则n-阶DSM噪声输出功率谱密度[6]。
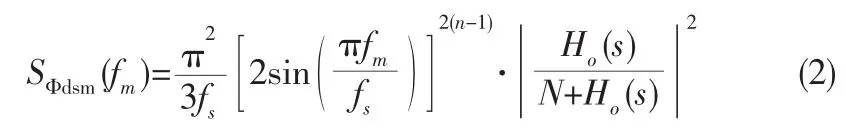
其中fs为DSM的时钟频率,N为分频器的分频比。上述的推导是假设模型为线性的情况下及不考虑噪声滤除器得出的,但是我们知道由于折叠噪声的存在,也就是说由于CP不匹配引起的非线性会加大DSM量化误差,从而进一步影响在PFD输入端的相位误差,因此有必要对式(2)进行修正。
作为将PFD输出脉冲转化为电流的电荷泵其实就是一个电流源,而组成电流源的元件是MOS晶体管,但实际上由于每个MOS晶体管的几何尺寸和阈值电压是无法做的一样,这样就会造成电流或电压不匹配出现。可以得出iup和idown不匹配电流的关系式[7]

其中ε为UP和DOWN电流不匹配因子(非线性度)。为了减小抖动,可以从两个方面着手,一是尽可能的降低CP的不匹配因子,二是减小在PFD输入端的相位误差。本论文就是从减小PFD输入端的相位误差为目的,后面会具体介绍如何减小输入端的相位误差。如图2所示,在PFD输入端,输入信号与分频器输出信号之间会存在到达时间差δ[k]。
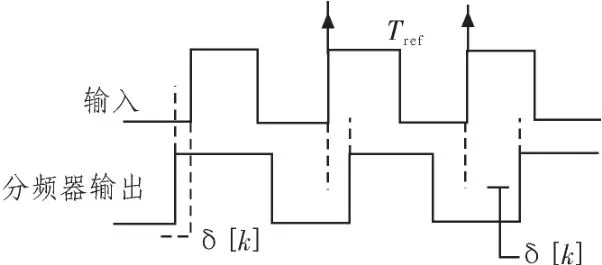
图2 PFD输入端波形示意图Fig.2 Diagram of PFD input waveform
假定δ[k]=tref[k]-tdiv[k],经过CP转换这个相位差为电流脉冲,被传递给环路滤波器的总电荷为
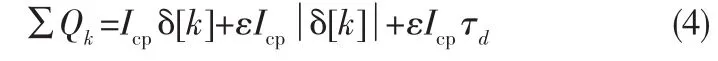
其中τd为延迟时间。在式(4)中,本文将重点考察第二项即CP不匹配项,设定δ[k]为高斯分布(均值为0,方差为),可得到的方差

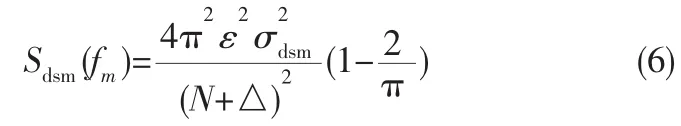
2 系统方案建模
在第二部分已经推导出,为了减小抖动峰值,在不匹配因子给定的情况下,就是要去减小在PFD输入端的相位误差。在小数分频频率合成器嵌入混合有限脉冲(FIR)滤除噪声技术可以减小量化噪声,但是这种方法无法减小折叠噪声[8]。为了对DSM量化噪声进行抑制,必须满足OLPF+ONF≥ODSM[8],其中OLPF为频率合成器环路滤波的阶数,ONF为噪声滤除器(NF)的阶数,ODSM为DSM的阶数。本文采用二阶环路滤波器,采用的DSM的拓扑结构是MBSL-I结构。多模分频器(MMFD)与噪NF连接共同构成一个反馈支路,而这样连接的目的不但可以抑制DSM量化噪声,而且还能减小折叠噪声产生的影响。下面对NF展开分析。
这里为了便于区分与组成频率合成器中的器件,组成噪声滤除器的3个器件分别为压控振荡器 (VCO_NF)、滤波器(LPF_NF)和鉴频鉴相器/电荷泵(PFD/CP_NF)。在其他文献中,组成噪声滤除器的元件的结构设计基本相同,一般设计要求是两个压控振荡器增益满足 Kvco.nf>Kvco,滤波器带宽满足 Blpf.nf<Blpf。而对于PFD/CP_NF的设计思想与PFD/CP基本一致,那就是尽量在设计的过程中使不匹配因子减小。综上考虑,如图3所示,在本文中的LPF_NF为二阶滤波器,这样可以减少极点带来的影响。PFD/CP_NF的结构与PFD/CP的设计结构一样。
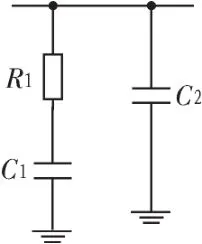
图3 二阶滤波器Fig.3 2-order filter
假定噪声滤除器的传输函数为HNF(s)

其中Hnf(s)=Kvco.nf·Zlpf.nf·Kpfd.nf,最后可以得出嵌入了噪声滤除器元件后在频率合成器输出端的量化噪声功率谱密度
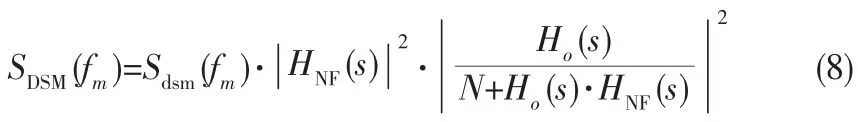
其中 Sdsm(fm)由式(9)求得,H(s)由式(5)得出。
上述只是对DSM量化噪声进行了分析。由图1可知,组成噪声滤除器有VCO和PFD/CP,因此还必须考虑噪声滤除器对量化噪声进行抑制的同时有没有引进其他相位噪声。下面对噪声滤波器中的VCO相位噪声以及PFD/CP_NF相位噪声进行分析,假定噪声滤除器中VCO相位噪声的功率谱密度为Svco.nf(fm)[9],可得出在频率合成器输出端的VCO输出噪声功率谱密度SVCO.NF(fm)
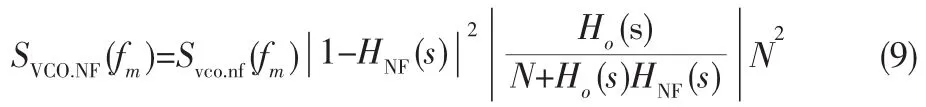
同理,设定噪声滤除器中PFD/CP_NF相位噪声的功率谱密度Scp.nf(fm)[10],可获得在输出端相位噪声功率谱密度SCP.NF(fm)。
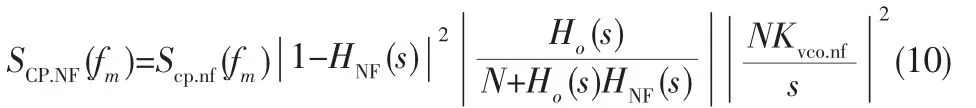
3 仿真结果分析
本论文的DSM的拓扑结构是采用MBSL-I型,这是由于多位量化比一位量化稳定性更好、信噪比更高。另外MBSL-I型比MASH的结构设计更灵活,MBSL-I的噪声传递函数为NTF(z)=(1-z-1)3(1-z-1+0.5z-2)[5]。为了直观的进行比较,本论文主要是对嵌入噪声滤除器的频率合成器与传统频率合成器各自输出量化噪声进行对比。表1为传统型和嵌入噪声滤除器的频率合成器各参数。假定不匹配因子ε=0.08,分频比N+α=165.3,图4为闭环幅频特性,可以看出噪声滤除器的带宽明显比环路带宽宽,从幅度图上可以看出从fm>100 kH噪声滤除器的幅度值相对于环路要高于10 dB。从幅度图可以看出,偏置频率从fm>100 kHz到fm<10 MHz噪声滤除器的增益裕度低于环路传递函数,但是fm>1 MHz后两种传递函数增益很小,也就是说对于在高频端,嵌入噪声滤波器不但不会破坏系统的稳定性,而且还可以滤除带外量化误差。

表1 模块参数Tab.1 Module parameters
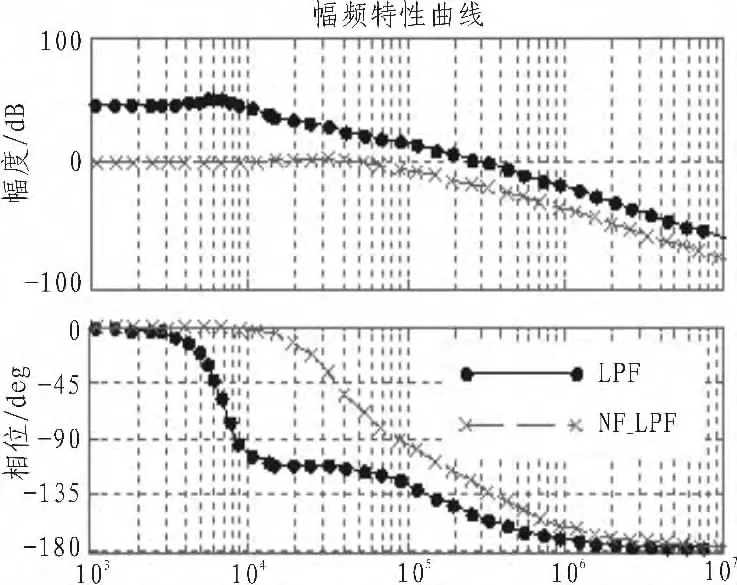
图4 闭环幅频特性Fig.4 Closed-loop amplitude frequency characteristics
如图5所示,得到嵌入噪声滤除器的频率合成器与传统频率合成器的两种传递函数,在偏置fm=900 kHz处,两种传递函数的幅度相差24.6 dB,与理论20×2×log(fm/fnf)=24.1 dB符合。
图6描述的是在两种传递函数下对DSM量化噪声输出的功率谱密度,从图中可以看出该传统模型在低频端的量化噪声有很好的抑制作用,但是随着频率的增大该模型对量化噪声的抑制能力明显减弱,对于抑制高阶DSM带外量化噪声,嵌入噪声滤除器的频率合成器优于传统频率合成器。以上说明对于高频段的DSM量化噪声该模型具有优良的抑制效果。图7为噪声滤波器各个模块所产生的相位噪声在频率合成器输出的功率谱密度。对于VCO产生的相位噪声在高频段被高通滤波器滤除,低频噪声可由低通滤波器滤除,从图中可以看出总得相位噪声在高频处的相位噪声得到了很好的衰减。换句话说,对带外的量化噪声有很好的滤除作用,而且总得相位噪声没有发生改变。这也说明,小数分频频率合成器嵌入噪声滤除器不会引进其他的相位噪声,而且这种新型频率合成器对带外量化噪声有非常好的衰减作用。
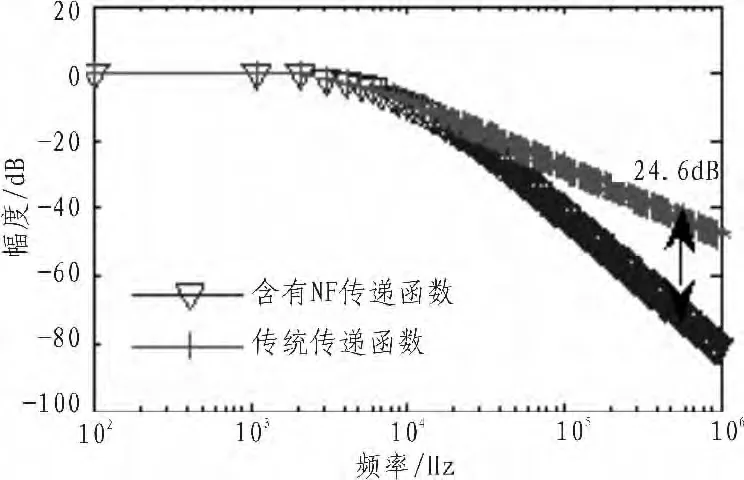
图5 传输函数Fig.5 Transfer function

图6 量化噪声功率谱密度Fig.6 Quantization noise power spectral density
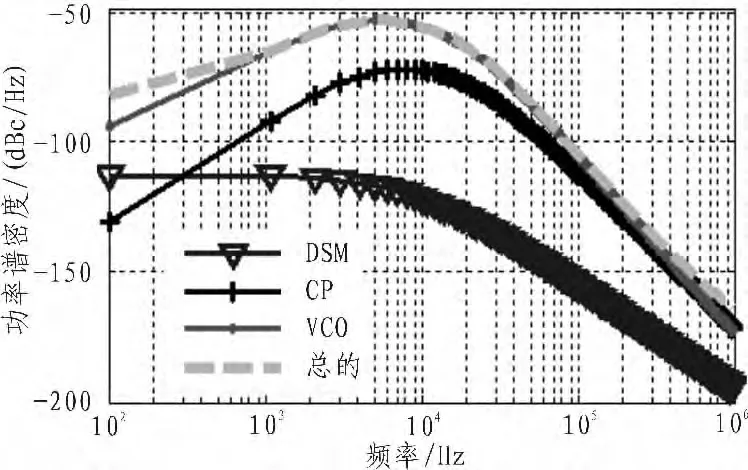
图7 新型频率合成器输出噪声功率谱Fig.7 Novel frequency synthesizer output noise PSD
4 结束语
文中首先对基于△-∑小数分频频率合成器中电荷泵电流不匹配引起的△-∑量化误差展开分析和建模,进而提出了一种新型DSM量化噪声滤除技术。通过MATLAB仿真验证该噪声滤除技术不仅可以对DSM带外量化噪声有衰减作用,而且对由于CP不匹配引起的DSM量化噪声也有抑制效果。
[1]Arora H,Klemmer N,Morizio J C,et al.Enhanced phase noise modeling of fractional-N frequency synthesizers[J].IEEE Trans.Circuits Syst.I:Reular papers,2005,52(2):379-395.
[2]YANG Yu-Che,YU Shi-An,LIU Yu-Hsuan.A quantization noise suppression technique for fractional frequency synthesizer[J].IEEE Journal of Solid State Circuits,2006,41(11):2500-2511.
[3]Lee H,Cho J K,Lee I,et al.A△-∑ fractional-N frequency synthesizer using a wide-band integrated VCO and a fast AFC technique for GSM/GPRS/WCDM applications[J].IEEE J.Solid-State Circuits,2004,39(7):1164-1169.
[4]Yu X,Sun Y,Rhee W.An FIR-embedded noise filtering method for Δ-Σ fractional-N PLL clock generators[J].IEEE J.Solid-State Circuits,2009,44(9):2426-2436.
[5]De B,Steyaert M.CMOS Fractional-N Synthesizers Design for High Spectral Purity and Monolithic Integration[M].Norwell,MA:Kluwer,2010.
[6]Hinz M,Konenkamp I,Horneber E H.Behavioral modeling and simulation of phase-locked loops for RF front ends[C]//inProc 43rd IEEE Midwest Symp.Circuits Syst,2000:194-197.
[7]Mao Xiao-jian,Yang Hua-zhong,Wang Hui.An analytical phase noise model of charge pump mismatch in sigma-delta frequency synthesizer[J].Analog Integr Circ Sig Process.2006(48):223-229.
[8]Levantino S,Collamati L,Samori C,et al.Folding of phase noise spectra in charge-pump phase-locked loops induced by frequency division[J].IEEE Trans.Circuits Syst.II:Exp Briefs,2010,57(9):671-675.
[9]De B,Muer,Steyaert M S J.A CMOS monolithic controlled fractional-N frequency synthesizer for DCS-1800[J].IEEE J.Solid-State Circuits,2002,37(7):835-844.
[10]Maffezzoni Paolo,Levatore Salvatore.Analysis of VCO phase noise in charge-pump phase-locked loops[J].IEEE Transaction on Circuits and Systems—I:Regular Papers,2012,59(10):2165-2175.
