基于萤火虫BP 神经网络的轴承故障诊断研究

翁胜龙，单外平，何国林

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

滚动轴承作为旋转机械的重要组成部分，经常工作在高温、高速、重载等恶劣环境，是容易产生故障的机械部件，机械失效归因于轴承故障的机率非常高[1]。因此，快速、准确的轴承故障监测对于机械设备的正常工作以及安全生产具有重大的意义。

神经网络，只需三层结构就能够实现任意精度的非线性映射[2]，以其良好的泛化性能在旋转机械故障诊断领域受到极大的重视和广泛推广[3-4]，如王志等[5]将神经网络应用于航空发动机的整机振动故障诊断，有效降低了虚报率。神经网络的标准算法为BP算法，其具有良好的可塑性、简易性，但在本质上为一种局部寻优算法，网络训练过程中对初始权值要求较高，易陷入局部极值点，导致神经网络的训练精度较低、无法有效识别故障。萤火虫算法，具备良好的全局寻优特性，能够有效地避免局部极值问题，一经提出，迅速引起国内外学者的广泛关注，已成功应用于生产调度、结构优化、图像处理、机器人等领域[6-7]。

为解决BP神经网络的局部极值问题，有效提高神经网络的训练性能，提出将萤火虫算法结合BP算法共同训练神经网络，在本质上，利用萤火虫算法的全局寻优特性对神经网络进行早期训练，有效避免局部极值点，得到优化的神经网络初始权值后，采用BP算法对神经网络做进一步精细训练，得到萤火虫BP神经网络诊断模型，并应用于轴承故障诊断。

1 萤火虫BP神经网络诊断模型

1.1 BP神经网络基本理论

神经网络[8]标准训练算法——BP算法，其核心是误差逆向传播，以三层神经结构为例，如图1所示。图1中，输入层、隐含层、输出层的节点数分别为R、S1、S2，隐含层和输出层的传递函数分别为f1和f2，各层连接权值分别为

图1 三层BP网络结构Fig.1 Three layer structure

训练误差逆向传播，对各层权值的进行修正，不断反复迭代，直到训练误差达到临界值，完成神经网络的训练。因此，BP神经网络的训练误差的收敛情况与初始权值直接相关，初始权值选取不当，极易导致训练过程陷入局部极小值点。但BP神经网络本身没有给出初始权值的确定方法，初始权值往往采用随机方式进行确定、从而导致BP神经网络的训练结果不稳定性较大。具有全局寻优特性的萤火虫算法，是群体智能的一个新的分支，寻优过程对初始条件的要求低，能够有效避免局部极值点。

为解决BP神经网络的局部极值问题，避免初始权值选取的盲目性，提出将萤火虫算法用于BP神经网络的初始权值的确定，从而解决BP神经网络的局部极值问题，提高神经网络的训练性能。

1.2 萤火虫算法

萤火虫算法的基本思想：每个优化问题的潜在解都是搜索空间内的萤火虫，所有萤火虫都有一个被优化的函数决定的适应值，适应值愈大，萤火虫亮度愈大。所有萤火虫之间都能相互吸引，亮度小的会朝向亮度大的移动，亮度最大的则进行随机移动。

在萤火虫算法[9]中，初始生成m个随机的萤火虫X=(X1,表示该萤火虫在D维搜索空间的位置，也是一个潜在解，然后通过迭代找到最优解。在每一次迭代中，萤火虫通过相互吸引来更新位置，若萤火虫j的亮度Ij小于萤火虫i的亮度Ii，则萤火虫i保持不动，萤火虫j朝向萤火虫i移动：

其中：i，j=1，2，…，m；d=1,2，…，D；k 为当前迭代次数；βo为吸引力系数，通常取βo=1。rij为萤火虫之间的欧式距离；γ为衰减系数，一般γ取1，控制吸引力随rij增加的衰减速度；α为随机性系数，α∈[0,1]，用于控制随机运动在移动过程的比重；为[0,1]分布的随机数。

1.3 萤火虫BP神经网络诊断模型

萤火虫BP神经网络诊断模型如图2所示，分3个部分：神经网络网络结构的确定、萤火虫算法优化、BP神经网络训练和预测，具体步骤如下：

1)确定神经网络的结构，网络的输入层节点数R由训练样本的特征维数确定，输出层节点数S2由训练样本的类别数决定，隐含层节点数S1靠人为选取。确定萤火虫种群个数m，设置 βo、γ 和 α。

2)计算连接权值长度L=R×S1+S1+S2×S1+S2连接权值长度L确定搜索空间的维度D，即D=L。

3)萤火虫种群初始化。

4)将各萤火虫i的位置向量Xi中元素赋值于连接权集合后 W1，b1W2，b2，将训练样本 Pq输入网络，得到输出 aq，q=1,2，…Q，通过式（1）计算训练误差ei来确定每个萤火虫的适应值fi，即 fi=-ei，从而得到萤火虫亮度 Ii，即 Ii=fi，i=1,2，…，m。

5)通过式（2）对种群进行一轮更新。

6)若种群中亮度最大的个体对应的训练误差e低于临界值e′或者达到最大迭代次数n1，则转到步骤7)，否则转到步骤4)。

7)将亮度最大的萤火虫的位置赋值于BP网络的连接权初值。

8)通过BP算法更新连接权值。

9)若BP算法到达最大迭代次数n2，或者训练误差低于临界值e″，则转到步骤10)，否则转到步骤8)。

10)训练结束，输入测试样本，得到预测结果。

图2 萤火虫BP神经网络诊断模型Fig.2 FA-BP neural network diagnosis model

2 轴承实验

实验装置由电机、齿轮减速机、联轴器、转速扭矩传感器、齿轮箱，磁粉加载器载荷组成,如图3所示。实测的轴承为NU204型滚动轴承,振动信号由安装在齿轮箱轴承座上方的加速度传感器来拾取。

图3 实验台示意图Fig.3 Test rig

实验中，轴的转速 600 r/min，载荷 50Nm，采样频率为51.2 kHz。轴承正常、内圈故障、外圈故障的振动加速度信号如图3所示。各类信号提取100组样本，每组样本含25 600个点。训练和测试样本各占总样本的50%。

从图4中可知，轴承内圈故障和外圈故障振动加速度信号中的冲击比正常情况下明显得多，冲击间隔具有一定的规律性；随转速波动，内外圈故障信号具有一定程度的非平稳性，在时域上直接进行诊断难度较大。

图4 轴承信号的时域图Fig.4 Bearing signals

为定量描述时域冲击特性，采用5个无量纲时域统计特征：峭度 xq(1)、波形指标 k(2)、脉冲指标 I(3)、峰值指标 C(4)、裕度指标L(5)来表征3类轴承信号，经归一化后，构输入神经网络。

2.1 参数设置

神经网络采用三层结构，隐含层节点数由训练样本特征维度确定为5，输入层节点数由3类故障模式确定为3，为对比不同隐含层节点下萤火虫BP神经网络的训练、诊断性能，隐含层节点数分别选取 2，3，4，5，6，7，8，9，10 共 9 种情况。

将萤火虫BP神经网络(FABPNN)用于3种故障模式的分类，并与BP神经网络(BPNN)、萤火虫神经网络(FANN)进行对比。萤火虫BP神经网络的参数设置为：种群数30，萤火虫训练的最大迭代次数 n1和误差临界值e′分别为100和0.1，BP算法训练的最大迭代次数n2和误差临界值e″分别为900 和 1e-3。 萤火虫神经网络，初始种群数 30，β0=1，γ=1，α=0.2。BP算法神经网络，学习步长lr=0.1。萤火虫初始种群在[-10,10]中随机生成。

2.2 结果分析

神经网络的训练过程为训练迭代次数达到1000或者训练误差收敛值达到误差临界值1e-3。图5为3种神经网络的一次训练过程中误差收敛情况对比。从图5可知，BP神经网络迭代到第23代，陷入极值点，训练误差无法进一步收敛，直到达到最大迭代次数1 000，训练误差仍处于0.1上。迭代次数从第1代开始，萤火虫神经网络、萤火虫BP神经网络分别迭代了10代、34代收敛到训练误差0.1，萤火虫神经网络的误差收敛速度为萤火虫BP神经网络的3.4倍；在第34代达到训练误差0.1之后，萤火虫BP神经网络开始采取BP算法进行，共迭代了5代达到误差临界值1e-3，而萤火虫神经网络在第10代之后共迭代了101代使训练误差由0.1下降到1e-3，在训练后期，萤火虫BP神经网络的误差收敛速度为萤火虫神经网络的20.2倍。因此，萤火虫BP神经网络在训练过程前期，采用萤火虫算法训练，能有效避免局部极值问题，在训练后期采用BP算法，能够完成神经网络的迅速收敛。

图5 训练误差收敛对比Fig.5 Error converging contrast

为避免试验结果的随机性，重复训练40次，各隐含层节点数下，3种神经网络的平均训练结果，如表1所示。

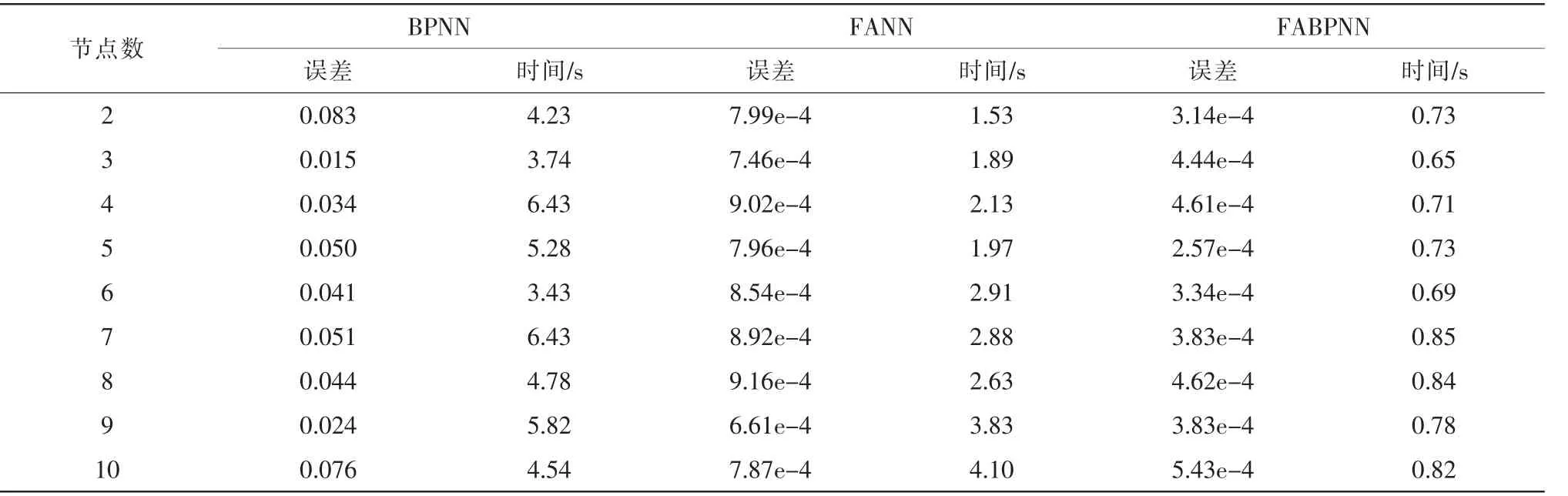
表1 3种神经网络的平均训练结果Tab.1 Average training results of three neural networks

从表1可知，在9种隐含层节点数下，BP神经网络的平均误差收敛结果都高于误差临界值1e-3，在隐含层节点数为3时，BP神经网络的训练误差为最小，为0.015。在各隐含层节点数下，萤火虫神经网络、萤火虫BP神经网络的平均误差收敛结果都低于临界值1e-3，并萤火虫BP神经网络的结果都为最低。在训练时间上，萤火虫BP神经网络具有明显的优势，在隐含层节点数10下，萤火虫BP神经网络的训练时间相比萤火虫神经网络、BP神经网络分别减少了3.08 s、3.52 s。因此，萤火虫BP神经网络的训练误差收敛速度明显优于BP神经网络和萤火虫神经网络。图6为3种神经网络训练模型在各个节点数下的平均测试结果。

图6 3种神经网络的识别正确率对比Fig.6 Contrast on the rate of three neural model

从图6可知，BP神经网络的识别诊断结果在不同隐含层节点数具有较大不同，其中在节点数3，达到最高识别率92.4%，在节点数6，达到最低识别率66.00%。在各个节点数下，萤火虫神经网络和萤火虫BP神经的识别结果都达到95%以上，并且萤火虫BP神经网络的识别率都为最高。在节点数10下，萤火虫BP神经网络的识别率达到最高，为99.47%，相比萤火虫神经网络、BP神经网络提高了1.6%、26.8%。

3 结论

提出将萤火虫算法结合BP算法共同训练神经网络，用于解决BP算法的局部极值问题，提高神经网络的训练误差收敛特性。

轴承实验表明，萤火虫BP神经网络的训练误差收敛速度相比于BP神经网络、萤火虫神经网络有显著提升，取得了99.47%的最高故障识别率。

[1]Randall R B,Antoni J.Rolling element bearing diagnostics—A tutorial[J].Mechanical Systems and Signal Processing,2011,25(2):485-520．

[2]Hornik K,Stinchcombe M,White H.Multilayer feed-forward networks are universal approximators[J].Neural Networks,1989,2(5):359-366.

[3]夏松波,张嘉钟,徐世昌等.旋转机械故障诊断技术的现状与展望[J].振动与冲击,1997,16(2):5-9,96.XIA Song-bo,ZHANG Jia-zhong,XU Shi-chang,et al.State of the art and development trends of fault diagnosis of rotating machinery[J].Journal of Vibration and Shock,1997,16(2):5-9,96.

[4]李巍华,张盛刚.基于改进证据理论及多神经网络融合的故障分类[J].机械工程学报,2010,46(9):93-99.LI Wei-hua,ZHANG Sheng-gang.Fault classification based on improved evidence theory and multiple neural network fusion[J].Journal of Mechanical Engineering,2010,46(9):93-99.

[5]王志,艾延廷,沙云东.基于BP神经网络的航空发动机整机振动故障诊断技术研究 [J].仪器仪表学报,2007,28(4):168-171.WANG Zhi,AI Yan-ting,SHA Yun-dong.Research on fault diagnosis technology of whole body vibration of aero-engine based on BP neural network[J].Chinese Journal of Scientific Instrument,2007,28(4):168-171.

[6]曾冰,李明富,张翼，等.基于萤火虫算法的装配序列规划研究[J].机械工程学报,2013,49(11):177-184.ZENG Bing,LI Ming-fu,ZHANG Yi,et al.Research on assembly sequence planning based on firefly algorithm[J].Journal of Mechanical Engineering,2013,49(11):177-184.

[7]IztokFister,IztokFister Jr,Xin-She Yang,et al.A comprehensive review of firefly algorithms[J].Swarm and Evolutionary Computation,2013,6:1-13.

[8]Rumelhart D E,Hinton G E.Learning representations by backpropagating errors[J].Nature,1986,323(11):533-536.

[9]Yang X H.Firefly algorithms for multimodal optimization[J].Stochastic Algorithms:Foundations and Applications,2009,5792:169-178.