JO－9159炸药强爆轰雨贡纽实验及产物的状态方程研究

王 辉，沈 飞，袁建飞，任新联，张 磊

（西安近代化学研究所，陕西西安710065）

引 言

高能炸药在极强的冲击加载作用下，可以产生压力和速度等均高于定常C－J爆轰状态的爆轰波，通常称为强爆轰或超压爆轰。国内外学者对炸药强爆轰的作用机理、爆轰波传播过程的实验观察、数值计算及其应用技术进行了大量研究［1－5］。其中，炸药爆轰产物的状态方程作为正确描述炸药作功能力及相互作用过程的基础，一直是研究人员关注的一个焦点。对于C－J爆轰状态下的产物状态方程，其参数值一般是通过圆筒试验结果标定的，适用范围为C－J压力至0．1GPa之间［6］，如果外推至强爆轰状态，其描述结果将会产生明显的偏差［7］。因此，针对强爆轰的特点，国内外学者提出了多种描述强爆轰产物的状态方程，其中最为典型的有改进的γ律方程、Lee－Tarver方程、Tang方程、JWL与γ律联合方程等［1－5，7－10］。在强爆轰产物状态方程参数的标定方面，P．K．Tang［8－9］通过分析PBX－9501、PBX－9502 炸药的强爆轰雨贡纽和声速实验数据，得到了修正的JWL 强爆轰产物状态方程（Tang方程）参数；邓农全［10］确定了DG01A 炸药的强爆轰产物多项式状态方程的参数；Liu Z．Y．等［7］确定了Comp B、LX－07等7 种炸药强爆轰产物的JWL与γ律联合方程参数；陈军等［2］修正了Tang方程的形式并确定了JB－9014炸药的强爆轰产物方程参数。但目前国内的相关研究仅能提供少数几种炸药的强爆轰产物状态方程参数，不能满足强爆轰条件、常规战斗部设计等方面的应用需求。

JO－9159炸药是一种能量高、感度较低的塑料黏结炸药［11］。本研究采用高速扫描相机测量JO－9159炸药强爆轰冲击波在不同试样中的传播时间，并由对比法获得JO－9159 炸药强爆轰产物的冲击雨贡纽数据［12］，最后根据实验结果标定产物状态方程的参数，为该炸药在强爆轰驱动、战斗部装药设计、材料物态方程研究等领域的应用提供参考。

1 实 验

1．1 材料及仪器

JO－9159炸药，西安近代化学研究所，配方（质量分数）：95%HMX 和5%黏结剂。采用模具压制成型，密度约为1．844g／cm3。

实验中铝基板和铝试样采用标准LY12硬铝材料，高速扫描相机采用苏州光学仪器厂生产的SJZ型转镜式高速扫描相机，扫描速度为6mm／μs。

1．2 实验装置

实验装置如图1所示，采用Φ100mm平面波透镜起爆主装药驱动铜飞片，经过一定距离的加速后撞击Φ100mm×3mm的铝基板。在铝基板下面分别安装Φ50mm×5mm的JO－9159炸药试样和Φ30mm×5mm的Y12铝试样，并在两种试样的后端面及基板的背面安装有机玻璃光探板。

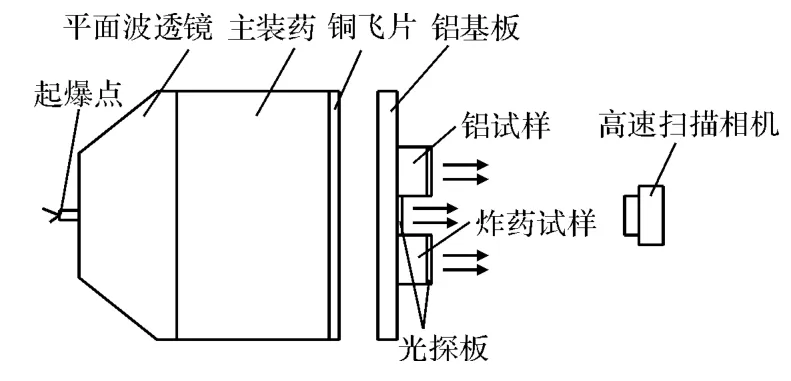
图1 雨贡纽实验装置示意图Fig．1 Schematic diagram of Hugoniot experiment setup

1．3 数据的获取

实验中，当入射冲击波经过基板后，激发基板与光探板之间的气隙发光，再经过样品激发样品与光探板之间的气隙发光，采用高速扫描相机记录冲击波到达基板背面和样品后端面的时间。结合样品的厚度，得到炸药试样中强爆轰波的传播速度及铝试样中的冲击波速度。利用实验数据及标准LY12硬铝的雨贡纽参数，可以计算出炸药的冲击状态参数（粒子速度和压力）。采用不同厚度的铜飞片及主装药组合来调节飞片的速度，从而获得不同冲击状态下的数据。

2 结果与分析

图2为高速相机拍摄的底片图，其中图2（a）为静态图，图2（b）为扫描记录的波形图。由于边侧稀疏的作用，试样边缘的冲击波速度降低，波形曲线的两侧翘起，这部分可去掉，分别将冲击波到达炸药试样扫描线b和铝试样背面扫描线c 与冲击波到达基板背面扫描线a 的位置进行对比，已知相机的扫描速度，对底片上的位置—时间进行转换可得到冲击波经过炸药试样的时间Δt1及经过LY12铝样品的时间Δt2。根据试样的厚度可计算出冲击波在炸药试样及铝试样中的平均速度，分别用D1和D2表示。共试验了4发，所获得的不同冲击状态下的数据见表1。

图2 高速相机拍摄的静态图（a）与扫描记录（b）Fig．2 Still picture and scanning record waveform figure of the high speed camera

表1 雨贡纽实验测量数据Table 1 Testing data on the Hugoniot experiment

获得炸药试样和铝试样中的冲击波速度后，再结合铝试样的雨贡纽关系，采用对比法可计算出炸药试样中冲击波后的粒子速度，图3是对比法的图解过程［12］，横坐标为试样的粒子速度，纵坐标为压力。

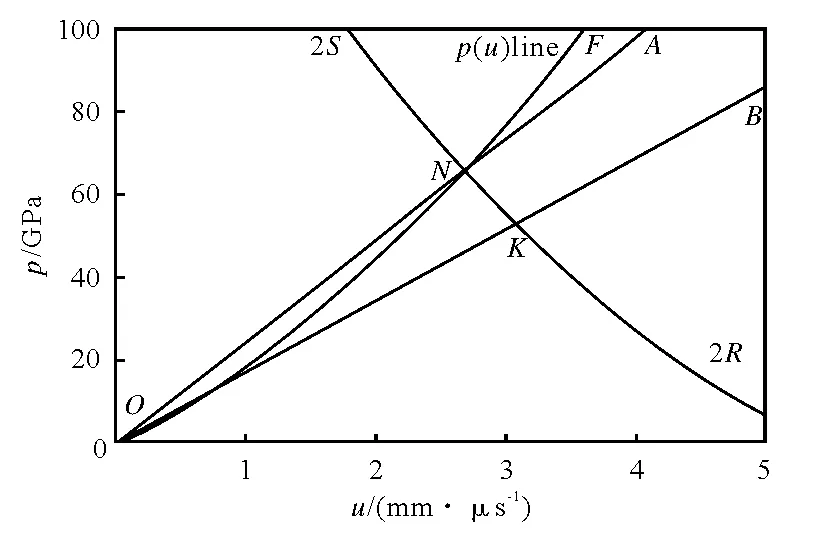
图3 对比法测雨贡纽线的图解Fig．3 Graphic solution of Hugoniot curve with antitheses method

图3中OA 线是铝试样的瑞利线，其表达式为

式中：ρ2为铝试样的密度。OF 线为LY12 铝试样的p－u雨贡纽线，其表达式为

式中：c0，λ 均为表征材料性质的特性常数，对于LY12铝试样，c0＝5．328mm／μs，λ＝1．338［2］。由式（1）和（2）可求出其交点N 所对应的粒子速度uN。于是可求出OF 线的反演线（2S－2R 线）的表达式为：

同时，OB 线是炸药试样的瑞利线，其斜率为ρ1D1（ρ1为炸药试样的密度）。OB 线与2S－2R 线的交点K 即为炸药试样中冲击波波后状态点，对应的速度为炸药试样中冲击波后的粒子速度。

得出炸药试样中冲击波后的粒子速度后，便可根据冲击波动量守恒关系（4）和质量守恒关系（5）计算出强爆轰产物的p－V 数据，结果如表2所示。

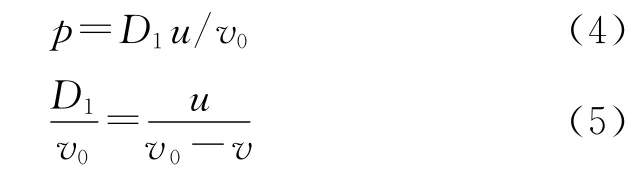
式中：v0和v分别是炸药样品的初始比容和冲击压缩后的比容；V＝v／v0为爆轰产物的相对比容。

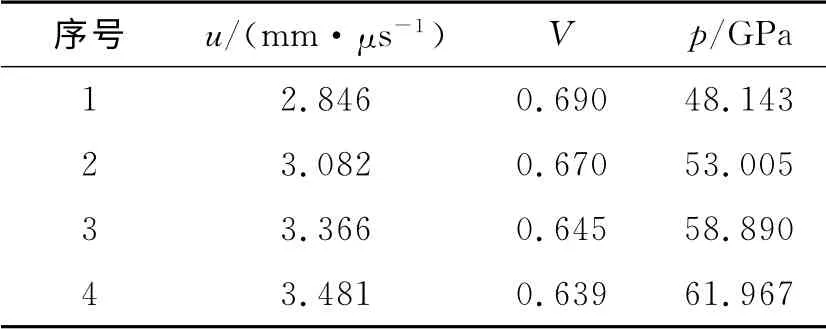
表2 JO－9159炸药强爆轰雨贡纽数据Table 2 Hugoniot data of the over－driven detonation of JO－9159explosive

3 强爆轰产物状态方程

JWL与γ律联合方程［7］由日本Kumamoto University材料冲击动力学实验室提出，将炸药CJ爆轰状态的JWL方程与γ律状态方程相结合，用于描述炸药强爆轰产物的状态方程。与其他几种典型的强爆轰产物状态方程形式相比，该方程有效地利用已知标准JWL状态方程和γ律状态方程的参数，仅加入一个调整参数m，在根据实验的强爆轰雨贡纽数据标定其产物状态方程参数时，可利用较少的实验数据确认参数m 值。同时参数m 的加入，使方程能较好地描述爆轰压力从C－J点过渡至高压时的爆轰产物状态，拟合的强爆轰雨贡纽曲线更具有物理意义，其表达式为：

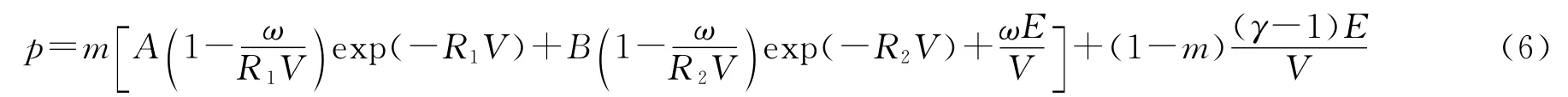
式中：E 为单位体积爆轰产物的内能；A、B、R1、R2、ω 均为炸药C－J爆轰产物的JWL 状态方程参数，γ为γ 律状态方程中的多方指数；m 是由实验确定的强爆轰状态参数。当爆轰压力等于或低于C－J爆轰状态时，m＝0或1分别表示选用JWL 方程或γ律方程计算爆轰压力。

在强爆轰状态中，爆轰产物的内能可表示为：

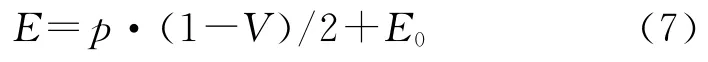
式中：E0为单位体积炸药的初始内能，则式（6）为隐式形式，为了表示方便，可将其转换为显式形式：

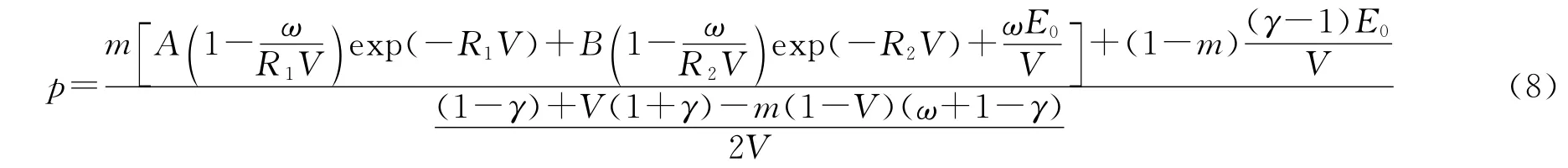
在强爆轰产物状态方程参数的确定过程中，还需要了解A、B、R1、R2、ω、γ的具体值。根据JO－9159炸药的圆筒试验结果［13］，可以确定出其爆轰产物的JWL状态方程参数，且根据文献［11］，多方指数γ可取为2．97，再采用最小二乘法对实验数据进行拟合并确定参数m 的值，所有参数的具体值如表3所示。图4为分别采用标准JWL 状态方程、γ 律状态方程和JWL 与γ 律联合方程对JO－9159炸药的强爆轰产物p－V 拟合曲线。从图4 中可以看出，在相同比容条件下，采用标准JWL 状态方程拟合强爆轰状态时，爆轰压力偏低；采用γ律状态方程拟合时，爆轰压力偏高；而采用JWL 与γ 律联合方程则可以较好地描述炸药的强爆轰产物状态，其拟合曲线与实验结果吻合较好。

表3 JO－9159炸药强爆轰产物状态方程参数Table 3 EOS parameters of over－driven detonation products of JO－9159explosive

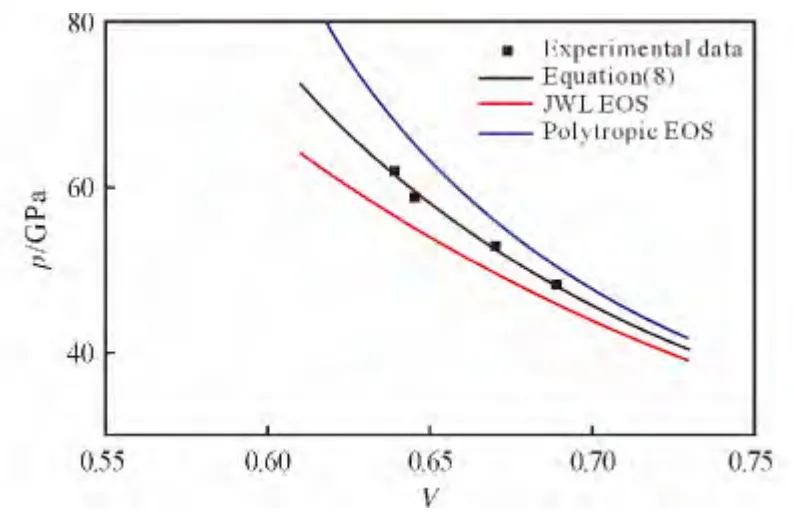
图4 JO－9159炸药强爆轰产物的p－V 曲线Fig．4 The p－Vcurves of over－driven detonation products of JO－9159explosive

4 结 论

（1）采用高速扫描相机获得JO－9159炸药强爆轰冲击波在炸药试样及标准铝试样中的传播速度，得到JO－9159炸药强爆轰产物的雨贡纽数据，并结合冲击波前后物理量守恒关系式得到强爆轰产物的p－V 数据。

（2）采用JO－9159炸药C－J爆轰产物的JWL状态方程或γ律状态方程外推拟合强爆轰产物状态时，其p－V 曲线与实验结果偏差较大，而采用JWL与γ联合方程的形式则可以较好地描述强爆轰产物的状态。

［1］ 张先锋，赵晓宁．夹层装药的超压爆轰研究综述［J］．含能材料，2011，19（3）：352－360．ZHANG Xian－feng，ZHAO Xiao－ning．Review on overdriven detonation of double layer high explosive charge［J］．Chinese Journal of Energetic Materials，2011，19（3）：352－360．

［2］ 陈军．超压爆轰产物状态及相关现象研究［D］．绵阳：中国工程物理研究院，2008．

［3］ 翟喆，张庆明．两级爆轰驱动装置发射弹丸的试验和数值模拟［J］．北京理工大学学报，2012，32（7）：677－680．ZHAI Zhe，ZHANG Qing－ming．Experimental and numerical research of launching high velocity projectile by two－stage detonation system［J］．Journal of Beijing Institute of Technology，2012，32（7）：677－680．

［4］ 文尚刚，赵锋，王建，等．气泡加载下炸药强爆轰驱动技术的初步实验研究［J］．高压物理学报，2011，25（1）：36－40．WEN Shang－gang，ZHAO Feng，WANG Jian，et al．Primary experimental study on driving technique of strong detonation using gas gun［J］．Chinese Journal of High Pressure Physics，2011，25（1）：36－40．

［5］ Liu Z Y，Nagano S，Itoh S．Overdriven detonation phenomenon in high explosive［J］．Shock Compression of Condensed Matter，1999：227－230．

［6］ 孙承纬，卫玉章，周之奎．应用爆轰物理［M］．北京：国防工业出版社，2000．

［7］ Liu Z Y．Overdriven detonation phenomenon and its application to ultra－high pressure generation［D］．Japan：Kumamo to University，2001．

［8］ Tang P K．A study of the overdriven behaviors of PBX 9501and PBX 9502［C］∥Proceedings of the 11th International Detonation Symposium．Colorado：Office of the Naval Research，1998：1058－1064．

［9］ Tang P K，Hixson R S．Modeling PBX 9501overdriven release experiments［J］．Shock Compression of Condensed Matter，1998：365－368．

［10］邓全农．过加载下固体炸药的实验研究和爆轰产物的高压状态方程［D］．绵阳：中国工程物理研究院，1989．

［11］董海山．高能炸药及相关物性能［M］．北京：科学出版社，1989．

［12］经福谦．实验物态方程导引［M］．第二版．北京：科学出版社，1999．

［13］张世文，华劲松，刘仓理，等．金属圆管内爆轰波的相互作用效应的数值模拟研究［J］．爆炸与冲击，2004，24（3）：219－225．ZHANG Shi－wen，HUA Jin－song，LIU Cang－li，et al．Research in numerical simulation on the effect under two detonation waves impacted in metallic tube［J］．Explosion and Shock Waves，2004，24（3）：219－225．