基于T-S模型的连续搅拌反应釜鲁棒L2-L∞控制

李艳辉，冯 岩

(东北石油大学电气信息工程学院，黑龙江大庆163318)

0 引言

连续搅拌反应釜(CSTR:Continuous Stirring Tank Reactor)是石化生产中十分重要的反应器，其控制质量在很大程度上决定生产的效率和产品指标，传统PID(Proportion Integration Differentiation)控制因整定参数不实时而难以达到满意效果。为此，国内外学者根据CSTR反应特点对其控制方法进行了广泛研究，如，Chyi等［1］针对非线性提出一种变结构控制策略，保证CSTR系统在有限时间内到达滑模面，然而系统易产生抖振现象而影响产品质量;WU［2］应用LMI(Linear Matrix Inequality)技术对CSTR进行模型预测控制，该方法假定CSTR系统是线性的，并忽略系统固有的时滞性。

T-S模糊模型是一种能以任意精度逼近非线性系统的模型［3-5］，众多学者在该模型的基础上对非线性系统的控制器和滤波器设计进行了深入研究，并得到良好的效果［6-8］。CAO等［7］基于T-S模糊模型针对含有确定参数的非线性CSTR系统进行稳定性分析和控制器设计，保证了系统稳定;WU等［8］假定非线性满足全局Lipschitz条件，利用LMI技术设计模糊随机系统的鲁棒H∞滤波器，收到了良好的滤波效果。

笔者考虑实际CSTR反应特点，针对进料组份产生的扰动和传热系数不规则变化引起的参数不确定等影响，研究鲁棒L2-L∞状态反馈控制问题。采用T-S模糊模型逼近无量纲化的机理模型，运用LMI技术给出该系统的L2-L∞性能准则，在此基础上进一步给出鲁棒L2-L∞状态反馈控制器存在的充分条件，并将控制器的设计转化为求解LMI的凸优化问题，更易于数值实现。通过仿真验证了该方法的可行性。

1 反应釜模糊模型的建立

物料以一定浓度C0和温度T0进入CSTR发生放热反应，操作目标是不断调整冷却剂温度T(t)使生成物浓度Ca(t)和反应器温度Ta(t)达到生产要求，如图1所示。基于能量守恒定律和化学动力学原理，该CSTR系统的无量纲化机理模型为［7］

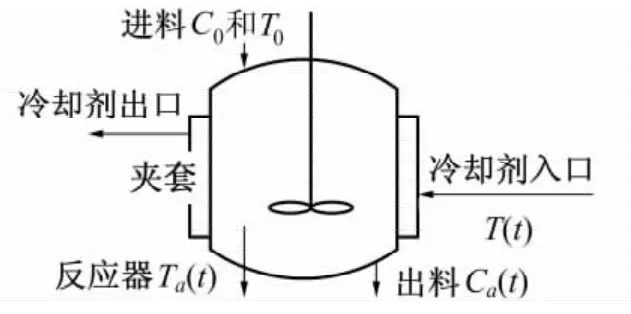
图1 CSTR示意图Fig.1 Schematic of the CSTR

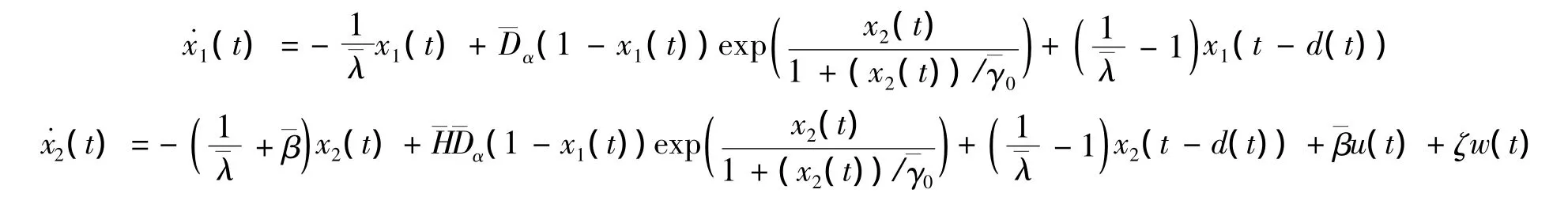
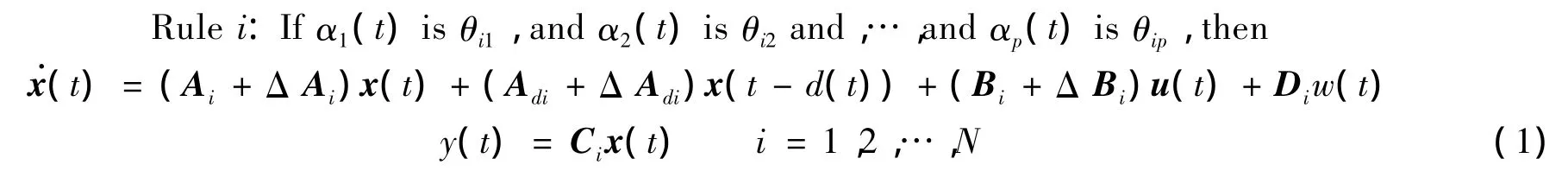
其中α1(t)，…，αp(t)为前件变量;θij为稳态平衡时温度的模糊集合;u(t)∈Rm;y(t)∈Rp为控制输出温度;d(t)满足0≤d(t)≤和0≤(t)≤＜∞(t≥0)，、为常量;w(t)∈L2［0，+∞);标量N为模糊规则的个数;为系统达到平衡点时对应的浓度和温度值。在平衡点有

假设 1 表示系统不确定性的矩阵 Δ Ai、Δ Adi和 Δ Bi满足:［Δ AiΔ AdiΔ Bi］=EFi(t)［GaiGdiGbi］，其中E，Gai，Gdi，Gbi为已知的适当维数实常数矩阵，Fi(t)为未知矩阵函数，且满足。

运用平行分配补偿算法［9］，对各模糊子空间设计相应的局部状态反馈控制器如下

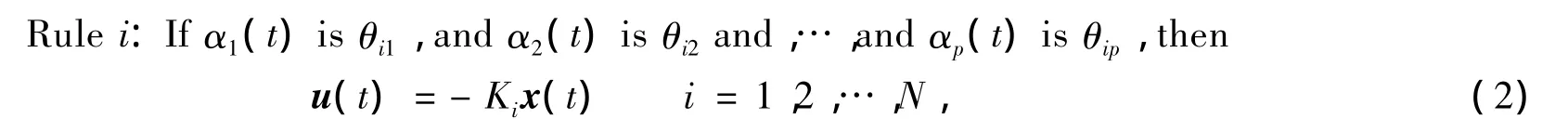
其中Ki∈Rm×n为待确定的对应子系统的状态反馈控制增益矩阵。于是整个模糊系统的状态反馈控制律为

将式(3)代入式(1)中，可得到整个模糊系统的状态方程

笔者针对建立的T-S闭环模糊系统式(4)设计稳定的鲁棒状态反馈控制器式(3)，从而保证闭环系统式(4)稳定且对于任意的非零w(t)，能满足L2-L∞性能约束:‖y(t)‖∞≤γ‖w(t)‖2。

2 主要结果

2.1 闭环模糊系统性能分析

首先给出容许的闭环模糊系统式(4)渐近稳定和满足鲁棒L2-L∞性能存在的充分条件，该条件为后续控制器的设计奠定基础。为证明笔者的主要结论，首先给出如下引理。

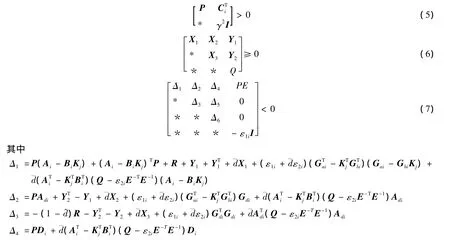
证明 构造Lyapunov函数:V(x(t))=V1(x(t))+V2(x(t))+V3(x(t))，其中V1(x(t))=xT(t)Px(t)，。

由假设1和引理1中1)可得到

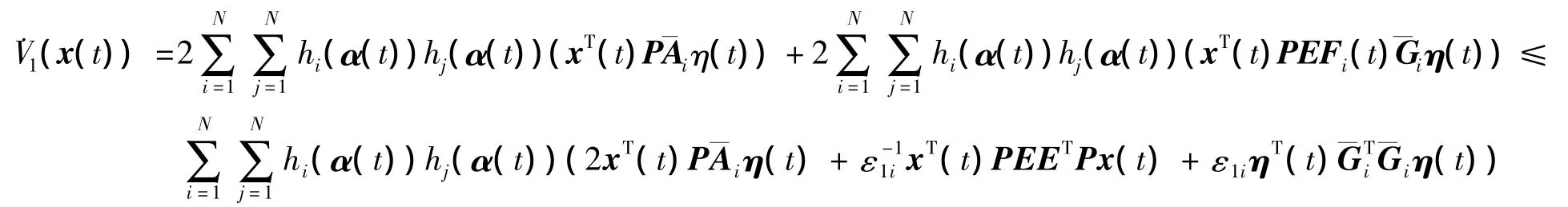
综上，通过对V(x(t))求取的导数，有

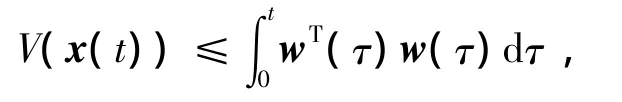
2.2 鲁棒L2-L∞控制器设计

根据定理1中的鲁棒L2-L∞性能准则，应用LMI技术，给出容许的鲁棒L2-L∞状态反馈控制器存在的充分条件。

如果式(9)～式(11)有可行解，则形如式(3)的鲁棒L2-L∞状态反馈控制器参数矩阵为

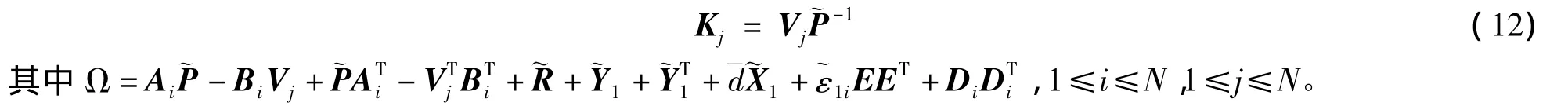
证明 对式(5)用diag［P-1I］进行全等变换，并令，可知式(9)成立;同理，对式(6)不等式两边同时左乘和右乘diag［P-1P-1P-1］，有

推论1 可以看出，对定理2中的式(9)～式(11)，可将γ2作为一个优化变量得到最优扰动衰减水平，即可通过求解如下凸优化问题设计系统(4)的最优鲁棒L2-L∞状态反馈控制器

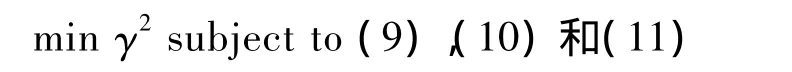
且控制器增益Kj可由式(12)求出。

3 仿真研究

规则1 ifx2(t)is small(x2(t)大约是0.886 2)，then

规则2 ifx2(t)is middle(x2(t)大约是2.752 0)，then

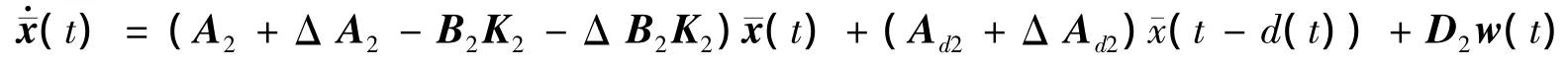
规则3 ifx2(t)is large(x2(t)大约是4.705 2)，then

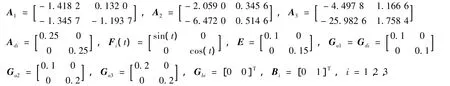
选择如下隶属度函数

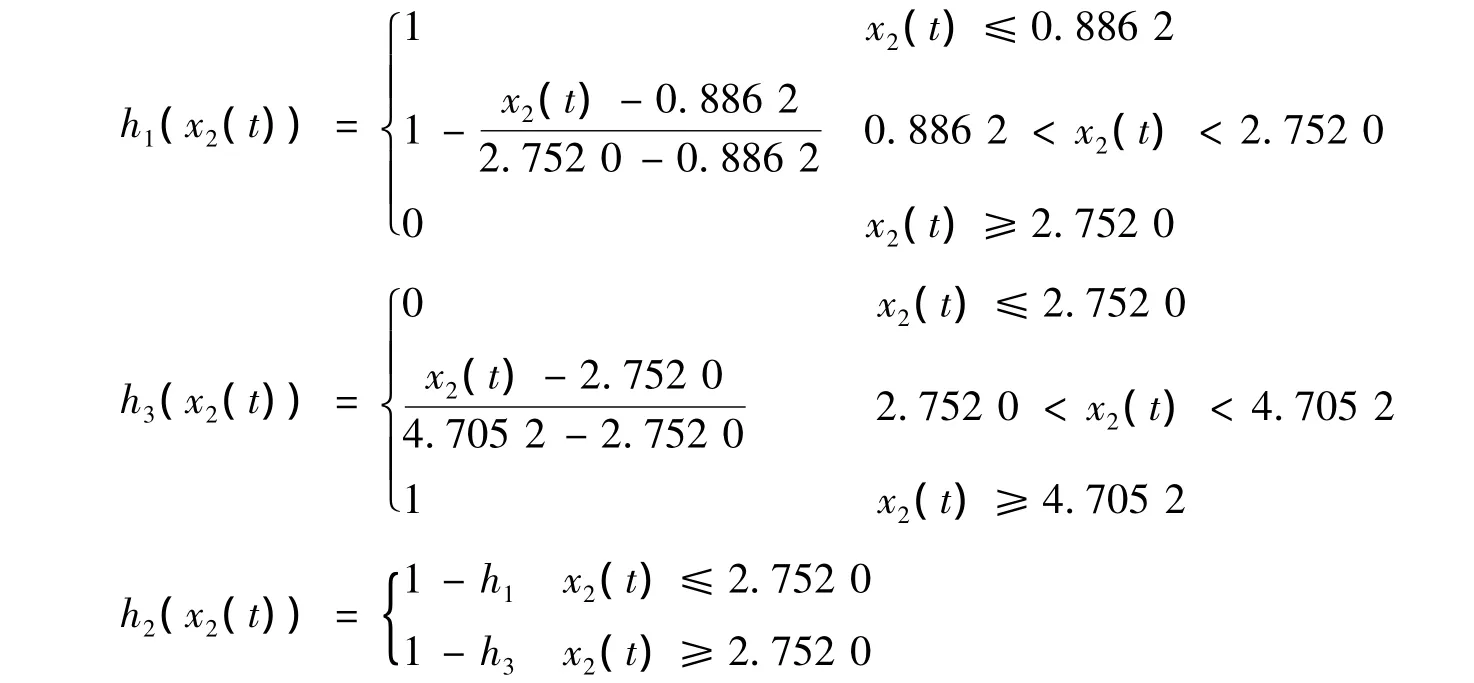
应用 LMI工具箱可得最优L2-L∞噪声抑制水平=0.2，相应状态反馈增益为 K1=［-1.345 7 98.806 2］，K2=［-6.406 6 98.383 4］，K3=［-26.222 8 99.016 2］。分别取系统初始状态x1(0)=［0.9 0.9］T、x2(0)=［2.7 2.7］T和x3(0)=［4.5 4.5］T，从图2a～图2c可以看出，不同初始状态下，CSTR系统稳定且满足给定的L2-L∞扰动抑制水平，表明设计的控制器有效。

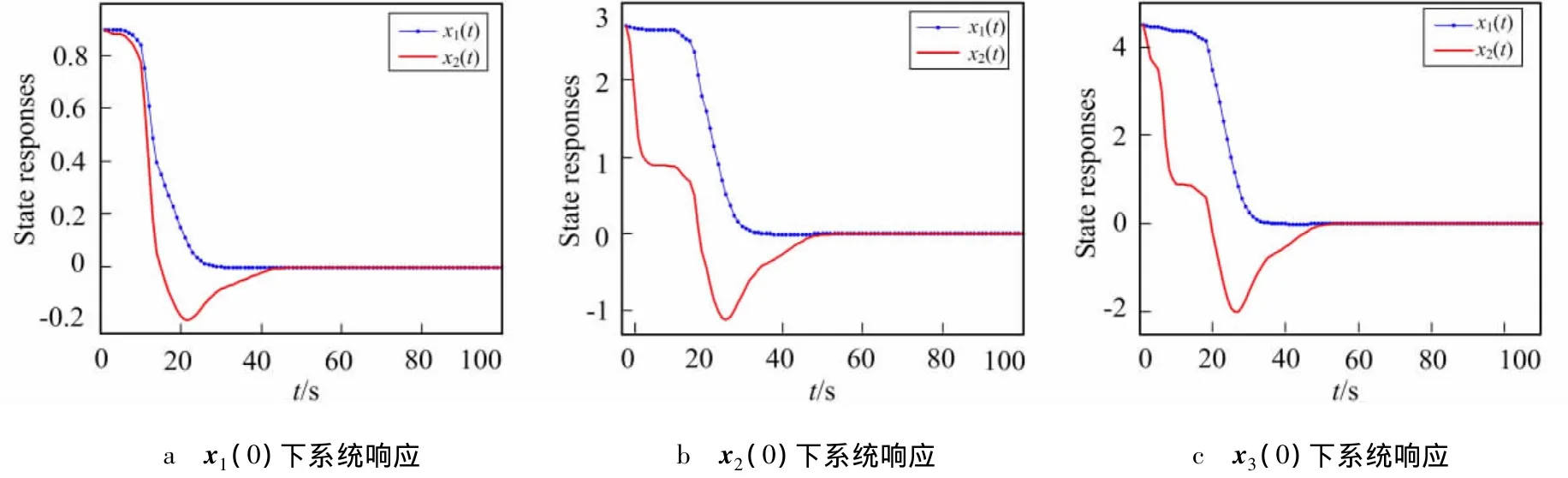
图2 x1(0)，x2(0)，x3(0)下系统响应Fig.2 System responses under x1(0)，x2(0)and x3(0)

4 结语

笔者针对实际CSTR反应系统，通过T-S模糊模型无限逼近反应对象，设计出了鲁棒L2-L∞状态反馈控制器。笔者将更易在线测量的反应器温度作为模糊规则的前件变量，并运用较为成熟的LMI技术求解全局控制器，方法简单容易实现。最后以仿真验证了基于T-S模糊模型设计的控制器可以满足控制要求。

［1］CHYI-TSONG，DAI CHYI-SHEN.Robust Controller Design for a Class of Nonlinear Uncertain Chemical Processes［J］.Journal of Process Control，2001，11(5):469-482.

［2］WU Fen.LMI-Based Robust Model Predictive Control and Its Application to an Industrial CSTR Problem ［J］.Journal of Process Control，2001，11(6):649-659.

［3］GAO Huijun，CHEN Tongwen.Stabilization of Nonlinear Systems under Variable Sampling:A Fuzzy Control Approach［J］.IEEE Transactions on Fuzzy Systems，2007，15(5):972-983.

［4］LEE H J，KIM D W.Robust Stabilization of T-S Fuzzy Systems:Fuzzy Static Output Feedback under Parametric Uncertainty［J］.International Journal of Control，Automation and Systems，2009，7(5):731-736.

［5］YOON T S，WANG Faguang，PARK S K，et al.Linearization of T-S Fuzzy Systems and RobustH∞Control［J］.Journal of Central South University of Technology:English Edition，2011，18(1):140-145.

［6］SAIFIA D，CHADLI M，LABIOD S，et al.RobustH∞Static Output Feedback Stabilization of T-S Fuzzy Systems Subject to Actuator Saturation ［J］.International Journal of Control，Automation and Systems，2012，10(3):613-622.

［7］CAO Yongyan，FRANK P M.Analysis and Synthesis of Nonlinear Time-Delay Systems via Fuzzy Control Approach［J］.IEEE Transactions on Fuzzy Systems，2000，8(2):200-211.

［8］WU Ligang，WANG Zidong.Fuzzy Filtering of Nonlinear Fuzzy Stochastic Systems with Time-Varying Delay［J］.Signal Processing，2009，89(9):1739-1753.

［9］WU Ligang，SU Xiaojie，SHI Peng，et al.A New Approach to Stability Analysis and Stabilization of Discrete-Time T-S Fuzzy Time-Varying Delay Systems［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2011，41(1):273-286.

［10］GASSARA H，EI HAJJAJI A，CHAABANE M.ReliableH∞Control for T-S Fuzzy Systems with Time Varying Delay and Actuator Faults ［C］// 18th Mediterranean Conference on Control and Automation，MED'10-Conference Proceedings.Marrakech，Morocco:［s.n.］，2010:1377-1382.