基于改进HWD 的小波阈值法图纸去噪研究

任伟建，任 璐，公丽颖，石 阔

(1.东北石油大学电气信息工程学院，黑龙江大庆 163318;2.胜利油田胜利软件有限责任公司，山东东营 257000)

基于改进HWD 的小波阈值法图纸去噪研究

任伟建1，任 璐1，公丽颖2，石 阔1

(1.东北石油大学电气信息工程学院，黑龙江大庆 163318;2.胜利油田胜利软件有限责任公司，山东东营 257000)

针对小波阈值法中的小波变换只能将图像分解到有限方向，而不能较好地表征图像多方向性的问题，用改进混合小波-方向滤波器组(HWD：Hybrid Wavelet-Directional filter banks)变换代替单纯小波变换，使在图像分解过程中更好地表征图像的多方向性，保存更多的图像信息;在分析小波阈值去噪原理的基础上，改变隶属度函数，构建HWD隶属度的权系数，从而避免因小波系数间存在幅值交叉使小波阈值法的应用受到限制。改进的HWD在损失最少图像小波系数的前提下，能最大限度地置零噪声小波系数。实际工程图纸去噪研究表明，改进的小波阈值法可在去除一定噪声的前提下，保留更多的工程图纸细节信息。

小波变换;方向滤波器;小波阈值法;工程图纸去噪

0 引 言

随着现代化工业的不断发展，工程图纸数字化已成为当前发展趋势，而数字化后的图纸图像在获取或传输过程中不可避免地会受到噪声污染，对其进行去噪处理也势必成为人们研究的热点。人们在研究实际图像与噪声分布特性的基础上，提出了许多行之有效的图像去噪理念［1］。小波变换在时域和空域上同时具有局部化特性，优于经典的傅立叶变换，所以在信号与图像去噪处理中得到了广泛应用［2］。

1994年，Donoho等［3］提出小波阈值萎缩方法(WaveShrink)，并给出了阈值公式。这种理论包括软阈值和硬阈值去噪两种方法，原理是根据信号和噪声在小波域内的不同分布特性采用不同的阈值方法，从而推动了小波理论的发展［4］。该方法利用图像小波分解后，各个子带图像的不同特性，选取不同的阈值，从而达到较好的去噪效果。但也同样受到高频信息的困扰［5］。基于这种分布特点，在小波域中，可置零绝对值相对较小的小波系数，而保留绝对值相对较大的小波系数，最后将剩余小波系数重构，得到估计去噪图像。

小波变换在一维信号处理中具有很好的特性，为处理二维图像，人们将一维小波变换成二维甚至高维，虽然达到了较好的去噪效果，但这种简单的由一维小波张量积形成的二维小波，只能捕获有限的方向信息，方向性的缺失使小波变换不能充分利用图像本身的几何正则性。因此，人们致力于发展一种新的高维函数的最优表示方法，目前提出了Ridgelet变换、Curvelet变换、Contourlet变换和WBCT(Wavelet-Based Contourlet Transform)变换等［6］。这些变换所采用的是基于支撑区间，表现出更高的方向敏感性，即具有各向异性(Anisotropy)，与小波变换相比，它们能更好地表现边缘特征，更适于进行多尺度的边缘增强处理。2004年，Eslami等［7］将Contourlet变换中拉普拉斯变换替换为无冗余小波变换，并对变换后的高频子带进行无冗余方向滤波(DFB：Directional Filter Bank)，即WBCT变换。该变换具有良好的无冗余特点，更有利于图像处理。然而，WBCT也存在严重振铃效应。为此，Eslami等［8］进一步研究了DFB与小波变换的特点，提出了混合小波-滤波器组(HWD：Hybrid Wavelet-Directional Filter banks)变换。其主要思想是假设小波子带与方向滤波器子带方向一致时，可取得最好效果，因此，水平子带(HL：High Low)(水平高频，垂直低频)与垂直子带(LH：Low High)(水平低频，垂直高频)应采用相应的半方向滤波器。HWD变换以无冗余且振铃效应最弱而成为多尺度几何分析的最高水平。然而传统的HWD采用FDFB(Full-tree DFB)对3个高频均进行FDFB分解，使HL与LH的低频信息也被分解，从而导致去噪后图像存在严重振铃效应。混合小波-方向滤波器组变换，首先对图像进行小波变换，然后对各子带进行md(md＜L，L为小波分解级数)级方向滤波器组分解，根据各细节的不同选用不同的滤波器，得到相应的方向信息。同时对最精细尺度上的系数使用DFB和改进型DFB增加小波分解的方向性特征，并将其应用到图像压缩中，取得了较好的效果［9］。由小波阈值法可知，代表图像细节信息的小波系数与代表噪声信息的小波系数同样主要分布于高频子带。对于细节信息丰富的工程图纸，细节信息与噪声信息的大量叠加是不可避免的。HWD变换对确定方向子带内的所有系数，都会以同样的权重予以增大，因此，对去除含丰富细节信息的工程图纸中的噪声，一般基于HWD变换的小波阈值法并不是最佳选择。

笔者提出一种基于模糊隶属度的HWD变换，利用隶属度函数区分小波系数代表图像及噪声信息程度的特点，使HWD变换可有选择地增大小波系数;对隶属度函数表征图像信息的性能以及改进HWD变换可有选择地增大小波系数的性能做出证明;利用笔者提出的基于改进混合小波-方向滤波器组变换的小波阈值去噪算法对实际工程图纸进行去噪处理，分析研究小波阈值法对工程图纸去噪效果的影响。

1 混合小波-方向滤波器组变换

DFB最早是由Bamberger等［10］提出的，它将频谱一定方式分解到多个楔形子带中，这些子带承载着各异方向的信息。

由于小波变换后的3个方向子带中其低频信息与高频信息的分布位置不同，对角HH方向的信息均为高频信息，应用FDFB对其进行方向滤波处理，可较好地捕获到图像的方向信息，而HL(LH)方向子带的高频信息主要分布在其水平(垂直)方向，低频信息则主要分布在其垂直(水平)方向。研究指出对低频子带进行DFB分解会产生严重的振铃效应，而对高频进行DFB分解其振铃则较弱。Eslami等［8］提出了半方向滤波器分解，即基于水平滤波的半方向DFB分解及基于垂直滤波的半方向DFB分解(VDFB：Vertical half-tree DFB)，并在此基础上提出(IHWD：Improve Hybrid Wavelets-Directional Filter Banks)变换，即根据不同小波分解方向选择不同方向滤波器，以避免对低频信息分解，并通过对小波系数加权处理将易产生振铃效应的信息尽量移至不易产生振铃效应的区域，以减轻振铃效应［11］。

其中whl为垂直子带权系数，wlh为水平子带权系数，方向角θ(i)表征该方向子带的方向，因此该方向角的正弦值sinθ(i)表征其偏离垂直轴的程度;同理，其余弦值cosθ(i)表征其偏离水平轴的程度。λ是常数，一般取0.2。将小波系数与相应子带内的权重系数相乘，即可得到加权后的小波系数。该HWD变换对应的图像分解流程如图1所示。

图1 基于IHWD变换的图像分解Fig.1 Image decomposition based on the IHWD transform

2 基于模糊隶属度的混合小波方向滤波器组变换

2.1 模糊隶属度函数

模糊逻辑可以处理任何不确定性的问题，而工程图纸所含噪声的大小和分布情况，以及经扫描输入后自身易产生粘连、交叉，都使待去噪的图纸图像具有一定的不确定性问题。张飞猛等［12］利用模糊逻辑设计模糊系统，并将其应用到含乘性噪声的合成孔径雷达图像去噪中，取得了良好的去噪效果。

设待处理的工程图纸图像的像素幅值Yi(n)，在采样时间间隔n的条件下，采样结果为Y0=Y(n)，则以Y0为中心，其邻域内的M+1个采样点的集合可表示为W(n)={Yj}，即

任意像素点的Si(n)值越小，其隶属度越高，此像素点属于原图像像素点的概率越大。最后根据上述Si(n)值与隶属的关系设计了模糊集，其三角模糊集坐标图如图2所示。其中u为该模糊集的宽度，其大小与该领域像素平均值相关联，一般取u=2.5σ。

根据三角模糊集坐标图，可得出隶属度与S(n)的关系式，设隶属度z为因变量，S(n)为自变量，则有

图2 三角模糊集坐标图Fig.2 Graph of triangle fuzzy set coordinate

2.2 改进混合小波-方向滤波器组变换

小波阈值法去噪的原理是对高频系数设定阈值，阈值以下的小波系数是由噪声引起的，将其置零。然而代表噪声的小波系数与代表图像细节的小波系数，其幅值界限不绝对清晰，存在交叉，这种现象对细节信息丰富的工程图纸去噪效果影响尤为严重。通常阈值的选取只是估计一个使上限图像系数与下限噪声系数同时最多的阈值，因此阈值法存在去噪不完整或图像信息损失过多的问题。为改善这一现象，笔者对HWD变换的对角高频同样设计加权系数

使对角高频系数同样可以有选择性地增大。将隶属度函数值z替代式(4)、式(5)及式(8)中的λ，得改进权系数

对于某一确定方向信息，若隶属度z值越大，其为图像信息的概率越大，则权系数也越大;若隶属度z值越小，其为图像信息的概率越小，即为噪声的概率越大，则其权系数越小。由此，经加权处理后的图像小波系数在减轻振铃效应的同时，有选择性地加大图像系数幅值与噪声系数幅值间的距离，为小波阈值法打下良好的基础。

综上所述，基于模糊隶属度的IHWD变换对应的图像分解流程如图3所示。

图3 基于模糊隶属度IHWD变换的图像分解Fig.3 Image decomposition based on fuzzy degree ofmembership of IHWD transform

3 改进HWD变换的相关证明

方向滤波器的引入使图像的纹理信息得到充分表现，为获取丰富的细节信息奠定重要基础。改进的方向滤波器不仅可实现对图像进行多方向分解，还可加大高频系数中图像细节系数与噪声系数间的幅值距离，并能最大程度减轻振铃效应。

定理1 改进的方向滤波器在实现对图像进行多方向分解的基础上，可有选择性地加大高频系数中图像细节系数与噪声系数间的幅值差。

证明 设图像观测信号

由此可知，若某一小波系数为图像小波系数的可能性越大，其图像小波系数与噪声系数间的幅值距离越大;反之越小。改进的方向滤波器不仅可实现对图像进行多方向分解，还可有选择性地加大高频系数中图像细节系数与噪声系数间的幅值距离。

证毕。

4 实际图纸去噪研究

结合改进HWD变换，笔者的小波阈值去噪法具体步骤如下：

1 )选取sym4小波基，确定3分解层数，在Matlab中对含噪图纸进行小波分解;

2 )将分解后的图纸图像经改进HWD变换处理，得到多方向小波系数，并给予每一方向高频子带上的小波系数相应权重;

3 )选取阈值及阈值函数;

4 )利用阈值和阈值函数处理经变换后的小波系数，得到估计小波系数;

5 )将此估计小波系数按原有方向除以相应权重，并利用小波反变换得到估计图像。

含噪工程图纸根据受污染程度大致可分为轻噪声背景下的一般工程图纸和强噪声背景下的严重污染工程图纸。将改进的小波阈值法应用到受污染情况不同的实际工程图纸去噪中，并将去噪结果与同等去噪条件下领域平均法和一般小波阈值法的去噪结果进行对比分析。

4.1 一般工程图纸去噪

受污染情况不是很严重的一般工程图纸，其噪声含量较轻，在现有技术及设备基础上可实现对其去噪处理，且处理后的效果较好，具有一定的后续处理及应用意义。

笔者依次选取5幅噪声量不同的一般工程图纸，在Matlab中利用鲁棒中值法及第1层小波分解高频系数估计每个图纸的噪声方差，分别利用领域平均法、一般小波阈值法和基于改进HWD小波阈值法对其进行去噪处理，并计算去噪后的均方误差与信噪比。其中一幅图纸去噪效果图如图4所示。5幅图纸去噪后均方误差及信噪比均值如表1所示。

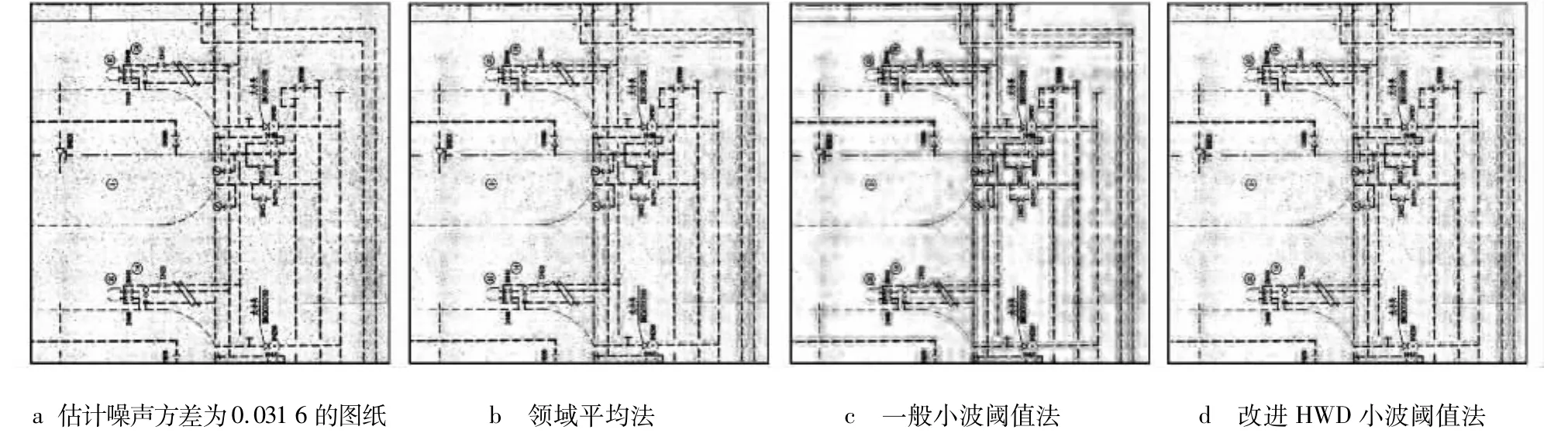
图4 各种去噪法对估计方差为0.031 6 cm2的图纸去噪结果Fig.4 The results of different denoisingmethod for the drawing with the estimate variance of 0.031 6 cm2

对于一般含噪情况的工程图纸，其去噪效果基本可以反映当前工程图纸去噪领域的研究水平及实现情况。从客观评价方式上，传统领域平均法，其均方误差小于小波阈值法，且信噪比高于小波阈值法，即传统去噪算法在噪声去除量上远优于小波阈值法;然而从主观评价法上，传统去噪算法虽然可以去除大量的噪声，但由于其去噪后图像较平滑，造成很多重要的图像纹理及细节信息的丢失，无法达到人们预想的效果，故失去了除噪的意义。小波阈值法根据小波变换后图像与噪声的不同特性，有选择地去除噪声，避免了图像信息的大量损失，主观上分析，其去噪效果远优于传统去噪算法。为了进一步提高小波阈值法的去噪性能，笔者对其进行了改进，从主观上，其在去除大量的噪声的前提下，保留了更多的图像细节信息，从客观上，其均方误差和信噪比虽仍不及传统去噪算法，但却远优于一般小波阈值法。

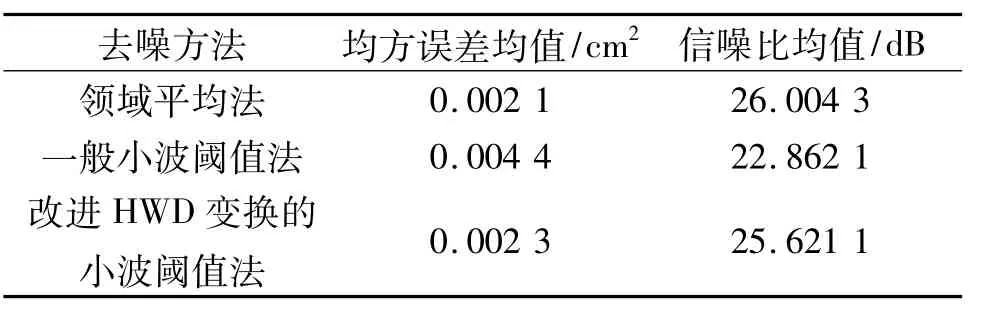
表1 各种去噪法去噪后均方误差与信噪比均值Tab.1 Average value ofmean square error and signal-noise ratio of different denoisingmethod

4.2 严重受污工程图纸去噪

受污染情况较严重的特殊工程图纸在实际工程项目中较少见，其特点是噪声含量较重，在现有技术及设备基础上不可实现对其去噪处理，即使可实现处理，其处理后的效果也未必很好，可能不具有后续处理及应用意义。然而这并不是说污染严重的图纸可以丢弃，有时对这种图纸的处理却是必要的，如有的图纸无副本，且相对重要或是有一定的收藏价值，而有的图纸只是部分受污染，其图纸仍含有部分可去噪处理的信息。因此，对于这两类图纸，尽管去噪效果不可预知，但去噪处理仍是必要的。

笔者依次选取5幅噪声量不同的严重受污工程图纸，在Matlab中利用鲁棒中值法及第1层小波分解高频系数估计每个图纸的噪声方差，分别利用不同方法对其进行去噪处理，并计算去噪后的均方误差与信噪比。其中一幅图纸去噪效果如图5所示。5幅图纸去噪后均方误差及信噪比均值如表2所示。

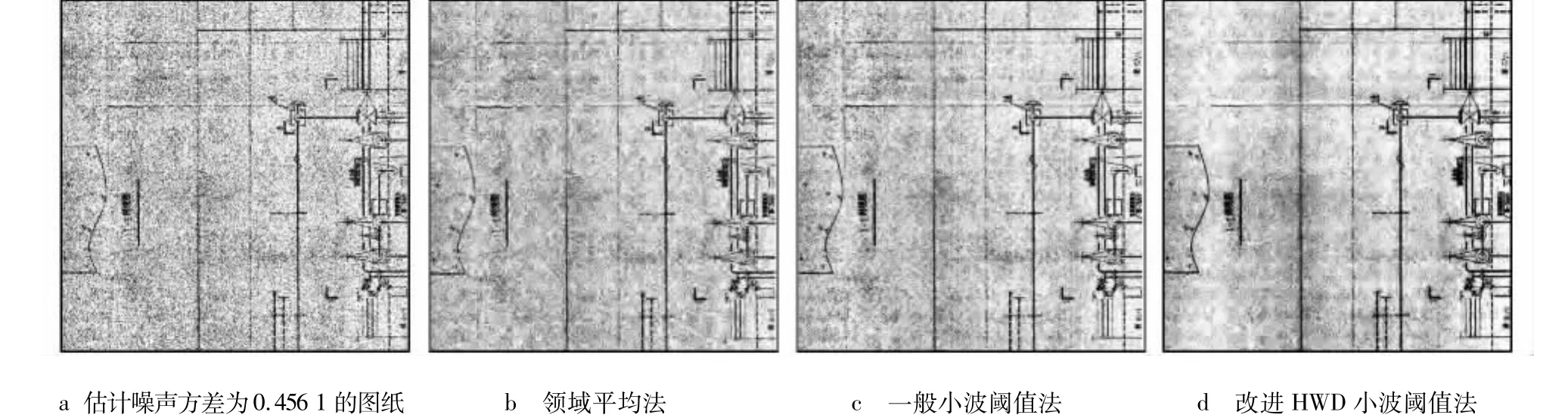
图5 各种去噪法对估计方差为0.456 1 cm2的图纸去噪结果Fig.5 The results of different denoisingmethod for the drawing with the estimate variance of 0.456 1 cm2

对于污染较严重的工程图纸，由于其特殊性，其去噪效果虽不足以反映当前工程图纸去噪领域的研究水平及实现情况，但仍具有一定的实际意义。因此，对这种含噪图纸的去噪研究也是必要的，与一般工程图纸去噪不同的是，无论是传统去噪法还是小波阈值法，其去噪效果都远不如一般工程图纸的去噪效果。传统去噪算法由于是以平滑为代价去除噪声，虽去除了大量噪声，但其强大噪声加剧了图像平滑的后果，使图像细节信息损失过多;小波阈值法区分噪声与图像的能力有限，噪声过强使图像信号淹没于强大的噪声信号中，因此其噪声去除量较少。

然而，改进小波阈值法由于在小波分解阶段加入模糊隶属度方向滤波器，使图像小波系数与噪声小波系数间的幅值差增大，从而提高了小波阈值法区分图像小波系数与噪声小波系数的能力，使改进的小波阈值法能较好地处理严重污染条件的工程图纸去噪。

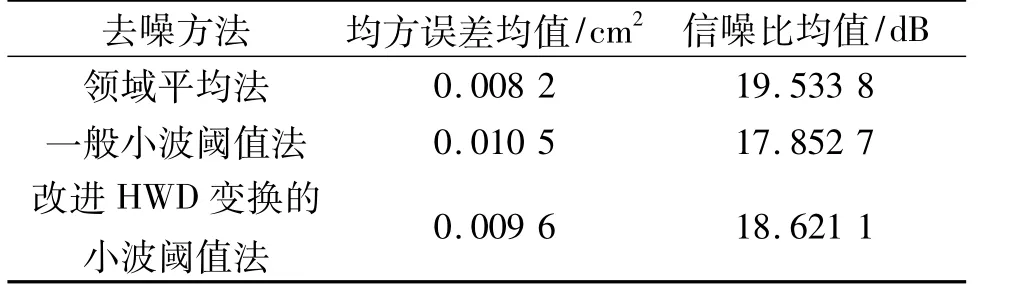
表2 各种去噪法去噪后均方误差与信噪比均值Tab.2 Average value ofmean square error and signal-noise ratio of different denoisingmethod

5 结语

笔者利用混合小波-方向滤波器变换代替单纯小波变换，改善小波分析只能将图像分解到3个方向的局限性，使更多的信息在小波变换中被表征利用;针对小波阈值法去噪实质是最大限度区分噪声与图像小波系数幅值，因此对混合小波-方向滤波器变换加入模糊隶属度函数，在图像分解阶段有选择地增大图像与噪声间的小波系数幅值差，提高小波阈值法的去噪性能，从而提高了工程图纸去噪质量。

［1］侯建华.基于小波及其统计特性的图像去噪方法研究［D］.武汉：华中科技大学控制科学与工程学院，2007.

HOU Jianhua.Research on Image Denoising Approach Based on Wavelet and Its Statistical Characteristics［D］.Wuhan：College of Control Science and Engineering，Huazhong University of Science and Technology，2007.

［2］倪虹霞，杨信昌，陈贺新.基于小波自适应阈值的图像去噪方法［J］.吉林大学学报：信息科学版，2005，22(4)：445-448.

NIHongxia，YANG Xinchang，CHEN Hexin.Desnoising Method Based on Adaptive Wavele Thresholding［J］.Journal of Jilin University：Information Science Edition，2005，22(4)：445-448.

［3］DONOHO D L，JOHNSTONE I.Ideal Spatial Adaptation via Wavelate Shrinkage［J］.Bianetrika，1994，81(3)：425-455.

［4］吴美璇.基于小波的图像阈值去噪方法［D］.重庆：重庆大学电子与通信工程学院，2012.

WU Meixuan.Denoising Method Based on Wavelet Image Threshold ［D］.Chongqing：College of Electronic and Communication Engineering，Chongqing University，2012.

［5］柳薇，马争鸣.基于边缘检测的图象小波阈值去噪方法［J］.中国图象图形学报，2002(8)：44-49.

LIUWei，MA Zhengming.Wavelet Image Threshold Denoising Based on Edge Detection［J］.Chinese Journal of Image and Graphics，2002(8)：44-49.

［6］李燕，刘斌.基于小波-全相位方向滤波器组变换的多聚焦图像融合［J］.计算机与现代化，2011(10)：76-80.

LIYan，LIU Bin.Multi-Focus Image Fusion UsingWavelet-Based All Phase Directional Filter Bank Transform［J］.Computer and Modernization，2011(10)：76-80.

［7］ESLAMIR，RADHA H.Wavelet-Based Contourlet Transform and Its Application to Image Coding［C］∥Proc IEEE Int Conf Image Processing.Hamiton：Image Processing Press，2004：3189-3192.

［8］ESLAMIR，RADHA H.A New Family of Nonredundant Transformations Using Hybrid Wavelets and Directional Filter Banks［J］.IEEE Trans on Image Processing，2007，14(4)：1152-1167.

［9］戴喆，彭进业，冯晓毅.一种基于HWD结构相似的图像质量评价方法［J］.电子设计工程，2013(1)：181-183.DAIZhe，PENG Jinye，FENG Xiaoyi.Imaga Quality Assessment Based on HWD Structural Similarity［J］.Electronic Design Engineering，2013(1)：181-183.

［10］BAMBERGER R H，SMITH M JT.A Filter Bank for the Direction Decomposition of Image：Theory and Design［J］.IEEE Transactions on Signal Processing，1992，40(4)：882-893.

［11］曹端午.图像的方向滤波及其在压缩中的应用研究［D］.广州：华南理工大学电子与信息学院，2011.

CAO Duanwu.Research on Image Directional Filtering and Its Application in Compression［D］.Guangzhou：Institute of Electronic and Information，South China University of Technology，2011.

［12］张飞猛，顾国华，凌冬冬，等.模糊方向滤波在SAR图像处理中的应用［J］.工程图学学报，2006(6)：69-73.

ZHANG Feimeng，GU Guohua，LING Dongdong，et al.Application of Fuzzy Direction Filtering in SAR Image Processing［J］.Journal of Engineering Graphics，2006(6)：69-73.

Research on Drawings Denoising Based on Improved Wavelet Threshold Algorithm with Hybrid Wavelet-Directional Filter Transform

RENWeijian1，REN Lu1，GONG Liying2，SHIKuo1
(1.College of Electrical and Information Engineering，Northeast Petroleum University，Daqing 163318，China;2.Shengli Oil Field Victorysoftware Company Limited，Dongying 257000，China)

For the defects that the image can only be decomposed into a finite orientation by the wavelet transformation，and multi-directional of image can not be better characterized，the directional filter is applied to themethod of wavelet threshold，namely，the HWD(Hybrid Wavelet-Directional filter banks)instead of the mere wavelet transform is used to better characterized the multi-directional of image and to retain more image information.To avoid the phenomenon of amplitude cross exists between image wavelet coefficients and noise wavelet coefficients，themethod ofwavelet thresholding was restricted by this shortcoming，membership function was changed based on the principle of the wavelet，and the membership weights of HWD was built by the membership function.The wavelet coefficients of noise were set to zero maximum with losing the image coefficients at least by this improved HWD.The wavelet coefficients of noise were set to zero maximum with losing the image coefficients at least by this improved HWD.The studies show thatmore details of engineering drawings can be retained by the improved wavelet threshold method beside removing some noise.

wavelet transform;directional filter;wavelet thresholding algorithm;engineering drawings denoising

TP391

A

1671-5896(2014)03-0239-08

2013-10-26

国家自然基金资助项目(61374127);黑龙江省教育厅科学技术研究基金资助项目(12511014);黑龙江省博士后科研基金资助项目(LBH-Q12143)

任伟建(1963— )，女，黑龙江泰来人，东北石油大学教授，博士生导师，主要从事复杂系统的建模与控制研究，(Tel)86-13845901386(E-mail)renwj@126.com。

何桂华)