高速SRM无位置传感器控制

马庆庆， 葛宝明， 毕大强， 李硕

(1.北京交通大学电气工程学院，北京100044;2.清华大学电力系统国家重点实验室，北京100084)

0 引言

开关磁阻电机调速系统(switched reluctance drive，SRD)是20世纪80年代中期发展起来的新型交流调速系统。自问世起，就因其结构简单，调速范围宽，运行效率高和低速启动转矩大等优点广受关注。开关磁阻电机通过定子各相绕组轮流导通产生电磁转矩，这就需要在转子轴端部安装光电编码器来检测转子位置。光电编码器不仅增加了成本，而且在恶劣的环境下，由于容易损坏而增加了系统的不可靠性，另外，在转子轴端部安装编码器也不利于减小SRM(swithed reluctance motor)体积。因此，无位置传感器研究受到国内外学者广泛关注［1－4］。

由于SRM的凸极效应，不同转子位置对应着不同磁链－电流曲线，文献［5］根据不同转子位置对应的磁链－电流簇建立电流、磁链、位置的三维表，并存储在内存中，通过检测相电流、相电压估算磁链，并通过查找三维表，得到当前转子位置，该方法需占用大量内存，且查表时间较长。在此基础上，文献［6］仅存储最大电感位置的磁链－电流曲线，通过检测相电流、相电压，估算磁链，然后查寻二维表，将估算得的磁链值和查寻得到的磁链值比较，以此作为换相时刻。但是，该方法仅适合单相轮流导通，即一相绕组关断另一相立刻导通，不适合SRM高速运行情况下的角度位置控制。文献［7－9］在推导电感模型基础上，构造基于电感模型的无位置传感器系统，该方法需要通过实验法或有限元法得到最大电感位置、最小电感位置以及两者中间位置的磁链－电流曲线，以此构建电感表达式，结合检测到的相电流和相电压，通过二分法估算转子位置角。与简化磁链法相比，该方法必须计算出较准确的电感模型，否则很难准确估算电机转子位置，且算法较复杂，不适合超高速SRM的无位置检测。例如，对于一个转速为50 000 r/min的4/2极SRM电机而言，一个相周期所需要时间为60 μs，因此算法的计算时间不能超过60 μs，否则所用算法将来不及估算转子位置。文献［10］对带状态观测器的无位置传感技术进行研究。该方法通过检测电机相电压和相电流，根据构建的状态空间模型，估算转子位置，其系统结构复杂，对微处理器实时性和计算功能要求很高。文献［11］提出一种基于频率调制技术的SRM无位置传感器控制系统，但该方法需要额外的检测电路。文献［12］针对超高速开关磁阻电机提出一种电流微分法检测换相时刻，以此来估算电机转子位置和转速，同样，该方法需要额外用于检测换相时刻的微分电路和滤波电路。另外，该检测方法仅适用于基速以上的调速范围，因此需要结合其他无位置检测法实现电机的高速无位置检测。文献［13］针对横向磁场直线开关磁阻电机的结构，利用各相绕组磁链在磁极中随位置不同产生的差异，提出了一种换相位置间接检测法，但该检测法需附加一套三相检测绕组来获取换相位置参考点。文献［14－17］通过检测相电流、相磁链，建立神经网络来估算转子位置，该方法需要对样本进行离线训练，训练样本选择的不准确或者数量不够，将对转子位置估计产生很大影响，并且工程应用中较难实现。

上述提到的无位置传感器法仅适合低速SRM的运行，当电机运行在高速或超高速情况下，越复杂的算法无疑对控制芯片运算速度提出更高要求，虽然传统简化磁链法算法简单、占用内存小、不需要额外检测电路，但仅适用于单相轮流导通条件下的PWM控制，这就无法采用角度位置控制来实现SRM的高速或超高速运行。此外，传统简化磁链法只能运行于固定的开关角，因此SRM效率受到影响。鉴于此，本文提出可实时调整开关角的无位置检测控制策略，该方法可以任意控制开通、关断角，实现低速和高速SRM的角度位置控制，改进后的算法不需要额外检测电路，算法简洁，为高速或超高速运行提供可能。为验证该无位置传感器检测法，分别以一台三相12/8极和一台两相4/2极 SRM为样机，设计了以TMS320LF2812为控制核心的数字控制器并编写相关算法，分别进行了低速和高速试验。

1 传统简化磁链法及实际磁链估算

磁链法于1991年由 J.Lyons等人首次提出［1］，其基本思想是:根据SRM不同转子位置的磁链－电流曲线簇，建立一个电流、磁链、位置的三维表，并存储在内存中。该算法需要计算多个不同转子位置的磁链－电流曲线，计算磁链－电流区线簇越多估算的转子位置越精确，但同时工作量越大，算法越复杂、计算时间越长，占用内存越大。这对主控制芯片提出了更高的要求，由于采样和计算时间受限制，很难将其应用在高速或超高速SRM无位置传感器控制器中。

在电机单相轮流导通条件下，SRM导通和关断位置检测可归结为:确定一个换相位置角，以该位置角对应的磁链作为当前导通相的参考磁链，将其与实际磁链比较，如果实际磁链小于参考磁链，表明实际转子位置未到达参考磁链对应的转子位置;反之，表明转子位置到达参考位置，即换相位置已到，开始导通下一相。该算法通过检测实际磁链是否达到参考磁链来判断是否需要换相，通常情况下，换相位置靠近电感最大位置，因此算法中只需存储最大电感位置的磁链－电流曲线作为参考磁链，这样，不仅减少工作量，也减小所需内存。

开关磁阻电机正常运行时，其第n相电压平衡方程可表示为

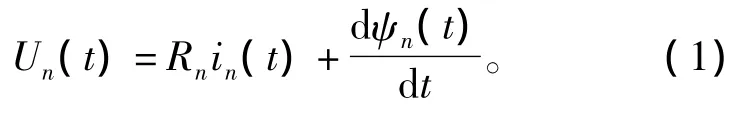
式中:Un(t)、in(t)、Rn分别表示第n相的相电压、相电流和绕组电阻;Ψn(t)是第n相磁链，它是绕组电流i和转子位置角θ的函数。

由式(1)得出一相绕组的磁链表达式为

将式(2)离散化可得

式(3)可进一步表示为

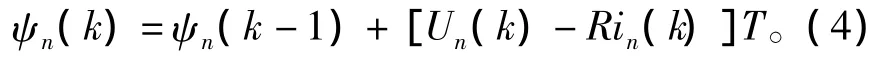
式中:T为采样计数周期;Un(k)、in(k)分别为n相第k个离散周期的相电压和相电流。

2 改进型简化磁链法

2.1 参考磁链的选取原则

由传统简化磁链法可知:算法中存储了最大电感位置的磁链－电流曲线，之后乘以一个小于1的系数k，得到对应换相位置的参考磁链值。然而，由于SRM磁链特性较强的非线性，采用上述简化磁链法很难得到良好的运行效果，因此，本文在分析传统简化磁链法选取参考磁链不足的基础上，提出新的选取原则。

SRM定子和转子是双凸极结构，转子每转过一个转子齿极，相电感重复一次，因此一个相周期内的位置角θT可表示为

式中，Nr为转子极数。

设SRM最小电感位置为0°，根据式(5)可知，4/2极和12/8极SRM的相周期分别为180°和45°，由于一个相周期内电感是对称的，所以，只需计算出半个周期内的磁化曲线。图1(a)和图1(b)分别为通过JMAG有限元仿真软件计算得到的4/2极和12/8极电机磁链－电流曲线簇，其中，4/2极电机每隔10°计算一条磁链－电流曲线;12/8极电机每隔2.5°计算一条磁链－电流曲线。从图1(a)和图1(b)可明显看出，两种不同结构SRM在最大电感位置和最小电感位置附近的磁链－电流曲线簇较密集，因此，选择最大电感位置作为参考磁链时，很小磁链误差将导致较大转子位置误差。另外，由于SRM磁链、相电流和转子位置角三者之间呈强烈的非线性关系，简单将最大电感位置的磁链－电流曲线乘以系数k难以准确求出任意开关角对应的参考磁链。因此，依据传统简化磁链法选择最大电感位置磁链－电流曲线将导致开关角的不准确性，这对于中低速SRM影响不大，但是对高速和超高速SRM来说，产生的误差将会更大，甚至造成换相混乱严重影响电机的运行。因此，本文选取较稀疏处的磁链－电流曲线作为参考磁链，如图1(a)和图1(b)箭头所示范围内的曲线。

图1 SRM电机磁化特性曲线簇Fig.1 SRM magnetization curves cluster

2.2 改进型简化磁链法控制策略

要实现SRM无位置传感器角度控制，必须选择参考位置角θref，同时使控制器输出如图2所示的角度位置控制信号。图中P为电机一个相周期位置角信号;A为输出控制信号;θon和θoff分别为设定的开通角和关断角(机械角度)。

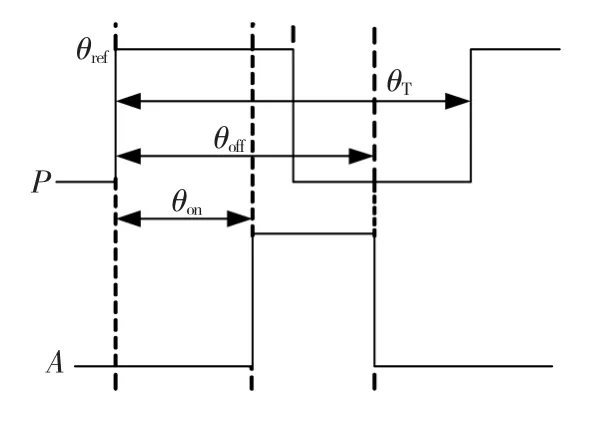
图2 SRM无位置传感器角度位置逻辑Fig.2 The sensorless SRM angular position control logic diagram

提出的无位置传感器SRM系统控制框图如图3所示。

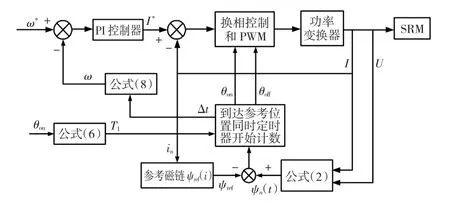
图3 SRM系统控制框图Fig.3 SRM control system diagram

其角度位置控制过程及换相策略如下:

1)对于三相12/8极样机，为准确确定其初始起动位置，在电机运行之前，首先给三相绕组同时注入一短时间电压脉冲，注入的电压脉冲必须能产生满足测试要求的响应电流;另外，产生的响应电流不至于使电机转子转动，然后比较三相响应电流的大小即可确定初始导通相，实现三相12/8极样机无反转起动。然而，对于传统两相4/2极样机，在电机启动时，存在死区，即当转子处于最大电感位置时无法启动，因此，设计不对称转子结构样机如图4所示，这样转子可以在任意角度自启动。由于该电机为两相SRM，不能再按照注入脉冲法实现无反转启动，但可通过如下方法实现启动:首先励磁电动机某相(例如A相)绕组，使其处于如图4所示最大电感位置，然后关断该相，导通另外一相(例如B相)绕组，从而可以顺利完成4/2极电动机起动过程。

2)SRM开通角控制可由定时器中断服务程序完成，当前瞬时磁链值估算可通过式(4)计算，依据参考磁链选取原则，选取转子位置角15°时的磁链作为12/8极SRM参考磁链;取转子位置角60°时的磁链作为4/2极SRM参考磁链。参考磁链Ψref(i)可通过最小二乘法拟合计算。

3)当第n相瞬时磁链值Ψn(i)小于参考磁链值Ψref(i)时，认为转子位置角未到达指定关断角，此时保持当前导通相不变;当第n相瞬时磁链值Ψn(i)=Ψref(i)，认为转子位置角到达关断角，此时关断当前导通相。开通角可通过实际转速实时计算得到，然后根据式(6)计算出T1，便可通过定时器控制下一相的开通时刻。

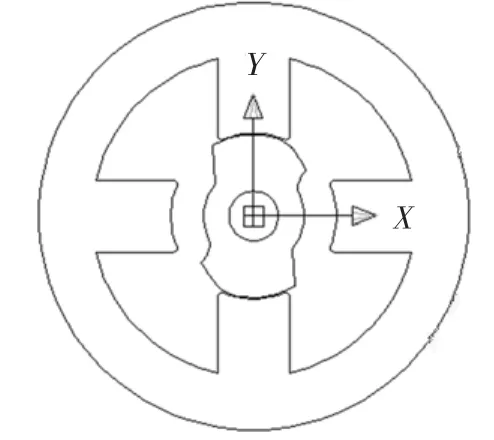
图4 可以自起动的4/2极SRM结构Fig.4 Self starting 4/2 pole SRM with the type of asymmetrical rotor

T1为开通角对应的延迟计数值，可表示为

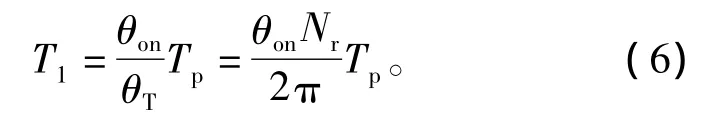
式中:Tp为一个相周期;θT内的计数值。

2.3 改进型简化磁链法转速与位置估算

在改进型简化磁链法控制策略中，由于选择的参考磁链为固定磁链值，所以SRM绕组两次关断时刻之间转子转过的角度刚好为一个相周期θT如图5所示，图中toff为关断时刻;Δθ为5个相周期;Δt为转过Δθ所用时间，可由两个关断时刻之间定时器中断服务程序执行次数计算。

图5 基于参考位置的速度估算Fig.5 Speed estimation based on reference position

当转速较高时，为了提高转速计算精度，SRM转子角速度表示为

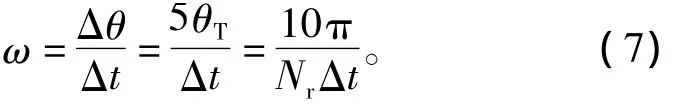
式中，ω为转子估算角速度。

将式(7)积分、离散化可得到任何转子位置的运动方程为

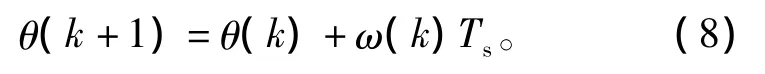
式中:Ts是采用周期;ω(k)是当前采样时刻转子角速度;θ(k)、θ(k+1)分别为当前采样时刻和下一采样时刻转子位置角。

由于式(8)中的积分每次都是从参考位置开始，故估算的转子位置不存在积分累计误差。

3 试验研究

3.1 试验样机

本文用一台低速样机和一台高速样机分别进行了无位置传感器控制策略的试验，两台样机参数如表1所示。

设计硬件电路并搭建如图6所示的无位置传感器SRM试验平台。试验中采用TMS320LF2812数字信号处理器作为控制器核心。该DSP具有强大的数字运算能力，一个指令周期仅为6.7 ns，这为较复杂的无位置控制算法在高速和超高速运行条件下提供可能。主功率电路采用如图7所示的不对称半桥型结构，该主电路控制灵活，可缺相运行。试验中，从三相12/8样机换到两相4/2样机时，只需将图7右边虚线框断开即可。SRM绕组的相电流和相电压分别由霍尔电流、电压传感器测量，经调理电路送到DSP的12位AD采样口，低速样机采样频率为6 kHz，为提高磁链计算精确度，高速样机采样频率选为15 kHz。另外，控制器还设计有电流、电压保护电路以及转子位置信号检测电路。所有的开通关断信号经过逻辑综合单元后再送给IGBT驱动芯片，功率驱动器件故障保护通过PDPINT的外部中断实现。

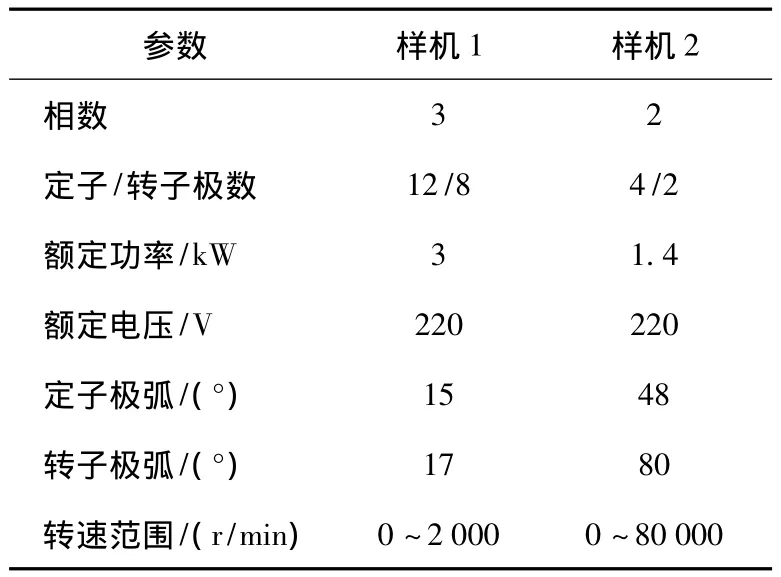
表1 样机结构参数Table 1 Parameters of prototype structure

图6 无位置传感器SRM实验平台Fig.6 Experiment platform for sensorless SRM

图7 不对称半桥型功率变换器Fig.7 Power converter with asymmetrical half-bridge

根据参考磁链的选取原则，选择不同的参考磁链意味着不同的关断角，为了简化控制算法，系统中给定参考磁链，即关断角固定不变。

为便于和实际转子位置比较，试验中保留光敏式位置传感器，其检测到的换相时刻用来与无位置传感器控制策略下的SRM换相时刻比较，以判断本文所采用方法的正确性和有效性。

3.2 试验结果

图8所示为给定开通角为4°，选取参考磁链为15°的12/8极样机稳态试验波形，从上到下依次为转速、实际转子位置信号、C相电流、B相实际磁链和B相参考磁链。其中，将AD采样得到的相电压和相电流代入式(4)可计算出实际磁链;B相参考磁链通过最小二乘法拟合。为了提高拟合的精度，试验中采用了分段拟合法，得到的分段多项式为

由图8可知，实际转子位置信号有3种状态，分别代表三相绕组A、B和C的开通状态。由(5)可知，12/8极SRM的相周期为45°，因此图中一个位置周期代表45°。图中电流为 C相电流波形，其开关角控制由B相实际磁链和参考磁链确定。从试验结果可以看出，C相电流开通角约为4°，这验证了根据式(5)可控制开通角，而关断角可根据选取不同的参考磁链确定。

图9所示为给定开通角为20°，参考磁链选取60°的4/2极高速SRM实验结果波形，从上到下分别为直流母线电压、相电流、估算转子位置、实际转子位置和转速波形。图中转子位置周期为90°，将实际转子位置和估算转子位置做差可得到如图10的误差波形，其中图10(a)为传统磁链法得到的转子位置误差，图10(b)为采用改进磁链法得到的转子位置误差，比较可知，前者误差最大值明显大于后者。

图11所示为给定开通角为4°，选取参考磁链为60°的样机稳态试验波形，从上到下分别为直流母线电压、实际转子位置脉冲、相电流、参考磁链、实际磁链和转速波形。其中，实际磁链可通过式(4)得到，参考磁链的分段多相式可表示为

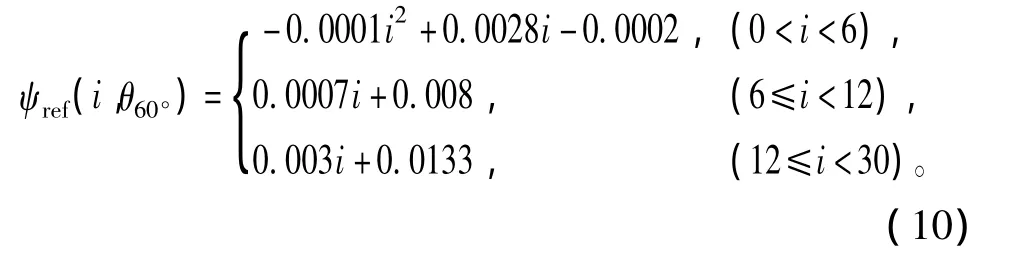
图8 12/8极SRM转速为1200r/min稳态试验波形Fig.8 Steady-state experimental waveforms for 12/8 pole SRM at 1 200 r/min

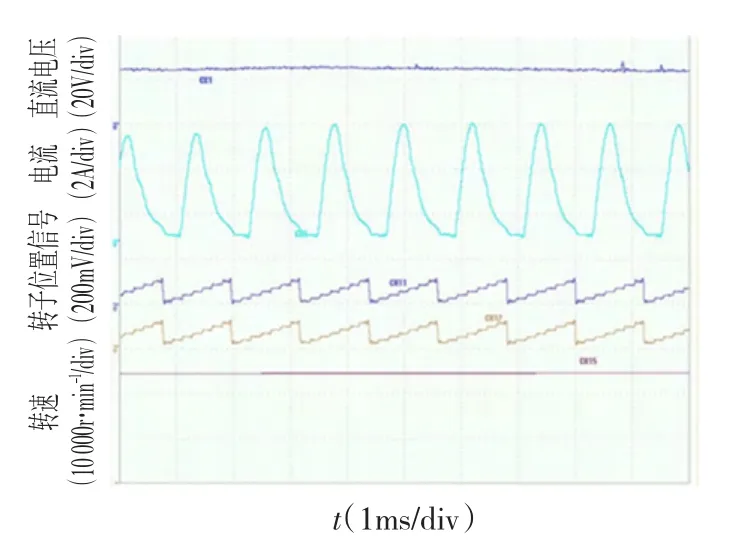
图9 4/2极SRM转速为24 000 r/min稳态试验波形Fig.9 Steady-state experimental waveform for 4/2 pole SRM at 24 000 r/min

图10 转速为24 000 r/min稳态位置误差Fig.10 Steady-state position error at 24 000 r/min

由图11可知，实际磁链和参考磁链的交叉点即为60°关断时刻，将给定的开通角代入式(6)，可计算出定时器计数值从而控制给定的开关角。由图11中实际位置信号脉冲可知，实际值和估算值存在一定的误差，这主要是由于转速较高，同样的采样频率，所计算得到的估算磁链误差更大所致。

图11 4/2极SRM转速为45 000 r/min稳态试验波形Fig.11 Steady-state experimental waveforms for 4/2 pole SRM at 45 000 r/min

图12所示为采用传统简化磁链法和改进的磁链法在不同电压下得到的速度响应曲线。从图中可明显看出，采用固定开关角控制策略时，当转速达到40 000 r/min时，由于此时相电流产生了制动转矩，即使增加直流母线电压也无法再提高转速，此时必须采用改进的简化磁链法来实现角度位置控制。同时，可以得出在同一电压下，采用改进后的算法电机转速明显高于传统的简化磁链法，突破了传统方法的局限性。

图12 4/2极SRM不同控制策略下的转速曲线Fig.12 4/2 pole SRM speed curves by different control strategy

4 结语

本文在简化磁链法的基础上，提出适应用于低速和高速SRM无位置传感器检测法，该方法可实现任意开通角和关断角的独立控制，为SRM在高速运行条件下的角度位置控制提供了有效方法。文中建立低速和高速样机有限元模型，总结简化磁链法中参考磁链的选取原则，在此基础上，详细论述提出的无位置传感器控制策略，给出转速和转子估算位置角计算公式。搭建试验平台，编写相关程序，分别在低速和高速样机上进行试验，试验结果表明提出的无位置检测控制策略可实现变角度控制，在低速和高速范围内均具有良好的性能，且和传统型简化磁链法相比，具有更高的检测精度，为SRM在低速和高速运行条件下无位置检测技术奠定基础。

［1］CAI Jun，DENG Zhiquan.Sensorless control of switched reluctance motor based on phase inductance vectors［J］.IEEE Transactions on Power Electronics，2012，17(10):3410 －3423.

［2］KRISHNAMURTHY M，EDRINGTON C S，FAHIMI B.Prediction of rotor position at standstill and rotating shaft condition in switched reluctance machines［J］.IEEE transactions on power electronics，2006，21(1):225 －233.

［3］GAO Hongwei，SALMASI F R，EHSANI M.Inductance modelbased sensorless control of the switched reluctance motor drive at low speed［J］.IEEE Transactions on Power Electronics，2004，19(2):1568－1573.

［4］张磊，刘闯，王云林，等.开关磁阻电机磁链特性检测与位置信号估计［J］.电机与控制学报，2013，17(2):28 －32.ZHANG Lei，LIU Chuang，WANG Yunlin，et al.Flux linkage characteristic detection of switched reluctance motor and the position estimate［J］.Electric Machines and Control，2013，17(2):28－32.

［5］GALLEGOS-Lopez G，KJAER P C，MILLER T J E.High-grade position estimation for SRM drives using flux linkage/current correction model［J］.IEEE Transactions on IA，1998，34(4):859－869.

［6］丘亦慧，詹琼华，马志源，等.基于简化磁链法的开关磁阻电机间接位置检测［J］.中国电机工程学报，2001，21(10):59 －62.QIU Yihui，ZHAN Qionghua，MA Zhiyuan，et al.The indirect position sensing of SRM on the basis of simplified flux method［J］.Proceedings of the CSEE，2001，21(10):59－62.

［7］蒯松岩，王鹏飞，黄玉龙.基于简化电感模型全域 SRM无位置传感器研究［J］.电机与控制学报，2013，17(10):52 －64.KUAI Songyan，WANG Pengfei，HUANG Yulong.The global position sensor-less technology of switched reluctance motor based on the simple inductance model［J］.Electric Machines and Control，2013，17(10):52 －64.

［8］陈坤华，孙玉坤，吴建兵，等.基于电感模型的开关磁阻电机无位置传感器技术［J］.电工技术学报，2006，21(11):71－75.CHEN Kunhua，SUN Yukun，WU Jianbing，et al.Inductance model-based sensorless control of the switched reluctance motors［J］.Transactions of China Electrotechnical Society，2006，21(11):71－75.

［9］SURESH G，FAHIMI B，RAHMAN K M，et al.Inductance based position encoding for sensorless SRM drives［C］//Power Electronics Specialists Conference，June 27，1999，Charleston，USA.1999:832－837.

［10］LUMSDAINE A，LANG J H.State observers for variable-reluctance motors［J］.IEEE Transactions on Industrial Electronics，1990，37(2):133 －142.

［11］EHSANI M，HUSAIN I，MAHAJAN S，et al.New modulation encoding techniques for indirect rotor position sensing in switched reluctance motors［J］.IEEE Transactions on Industry Applications，1994，30(1):85 －91.

［12］BATEMAN C J，MECROW B C.Sensorless operation of an ultrahigh-speed switched reluctance machine［J］.IEEE Transations on Industry Applications，2010，46(6):2329 －2337.

［13］张艺腾，葛宝明.横向磁场直线开关磁阻电机换相位置的间接检测方法［J］.机车电传动，2006，(2):49－52.ZHANG Yiteng，GE Baoming.Indirect detecting method of commutation position for transverse flux linear switched reluctance Motor［J］.Electric Drive for Locomotives，2006(2):49 － 52.

［14］蒯松岩，张旭隆，王其虎，等.开关磁阻电机神经网络无位置传感器控制［J］.电机与控制学报，2011，15(8):18 －22.KUAI Songyan，ZHANG Xulong，WANG Qihu，et al.Position sensorless control of SRM using neural network［J］.Electric Machines and Control，2011，15(8):18 － 22.

［15］ZHONG R，WANG Y B，XU Y Z.Position sensorless control of switched reluctance motors based on improved neural network［J］.IET Electric Power Applications，2012，6(2):111 －121.

［16］MAKWANA J A，AGARWAL P，SRIVASTAVA S P.ANN based sensorless rotor position estimation for the switched reluctance motor［C］//Nirma University International Conference，Dec.8 －10，2011，Ahmedabad Gujarat.2011:1 －6.

［17］杨先有，易灵芝，段斌，等.开关磁阻电机调速系统BP神经网络建模［J］.电机与控制学报，2008，12(4):447 －450.YANG Xianyou，YI Lingzhi，DUAN Bin，et al.Modeling switched reluctance driving with the BP neural network［J］.Electric Machines and Control，2008，12(4):447 － 450.