基于LCL滤波器的谐波抑制型能量回馈器的研究

王 燕，赵孔仓，贺慧勇，唐立军，赵 丹，廖文平

(长沙理工大学物理与电子科学学院，湖南长沙410114)

0 引言

随着社会的快速发展，能量的循环利用越来越受到人们的重视，然而交流变频调速系统的制动往往就是采用能耗制动［1-3］。这样不但白白浪费了多余的能量，而且消耗能量产生的热量对变频器的正常工作也带来了很大的影响。能量回馈器是一种再生制动装置，它能把多余的电能回馈到电网，具有很大的使用价值。然而由于电网电压含有大量谐波，并且时而会不稳定［4］，如果能量回馈器的抗干扰能力和稳定性不够好，则能量回馈器的工作效率会很低，并且回馈到电网电压中的电流谐波也会很大，这样会对电网电压造成谐波污染，缩短机器的使用寿命。现在也有很多人对能量回馈器开始了研究设计工作，但是真正应用到实际生产中的抗干扰能力强、稳定性高的能量回馈器很少［5-7］。基于此，本研究开始了对具有抗干扰能力强，稳定性高的能量回馈器的研究。

LCL 滤波器在高频阶段具有较好的滤波特性，但还不足以完全抑制谐波干扰［8-9］，并且LCL 滤波器会使系统产生谐振尖峰。传统的去掉谐振尖锋的方法是在电容支路加电阻，但是这种方法会增加系统的功耗［10］，对提高能量回馈效率无益。同时，网侧电流环和电容电流环双环控制具有很高稳定性和快速性等动静态特性，但是不能抑制电网电压的扰动带来的谐波干扰。比例谐振控制可以对特定频率正弦信号实现无静差控制，具有较好动态性能，但是它只对特定频率的谐波具有抑制作用，因此对不同频率的谐波需要不同的谐振控制器，这无疑增加了控制的复杂性。电网电压前馈控制可以很好地对电网的波动进行抑制，并且结构简单。

本研究提出通过有源阻尼来消除谐振尖峰，即利用电容电流反馈形成虚拟电阻的方式增加谐振阻尼。同时提出了基于电网电压前馈的电流双环控制策略。

1 LCL 能量回馈器的数学模型

三相LCL 能量回馈器的主电路拓扑结构如图1所示。

图1 三相LCL 型能量回馈器的主电路拓扑结构

1.1 三相abc 静止坐标系下的数学模型

根据KCL 和KVL 定律，可得有源逆变器侧输出电流、三相网侧并网电流、滤波电容电压和直流母线电容电压等的描述方程。

各桥壁输出电压是:

逆变桥侧输出电感Li、电流ii满足:

式中:uCoN—直流母线负极与滤波器电容中电之间的电位差。

三线制系统满足iia+iib+iic=0，iaa+iab+iac=0，将上式相加可得:

考虑到系统三相对称性，即满足uca+ucb+ucc=0，则式(3)可改写为:

将式(4)代入式(2)中，可得到:

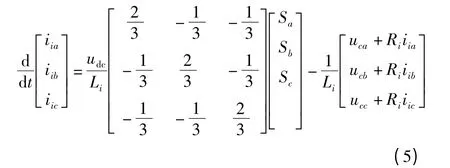
令:

则式(5)可化简为:

电网侧滤波器输出并网电流ig满足:

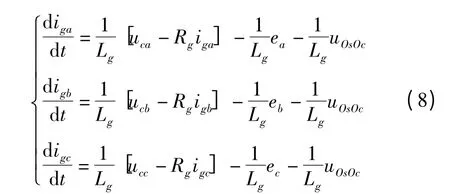
式中:uOsOc—三相电网中电与滤波器电容中点之间的点位差。

考虑系统三相对称，满足uOsOc=0，上式可写为:

滤波电容电压uc满足:

滤波母线电压udc满足:

1.2 同步旋转dq 坐标系下的数学模型

在三相三线制有源逆变器系统中，三相电压、电流并不是独立变量，可以采用两相同步旋转dq 坐标系对系统进行描述，以简化并网逆变器模型。

从而将式(7)进行旋转变换，得:

令uid=udcSd，uiq=udcSq，代入上式可化简为:

同样的，将式(9)进行旋转变换，可得:

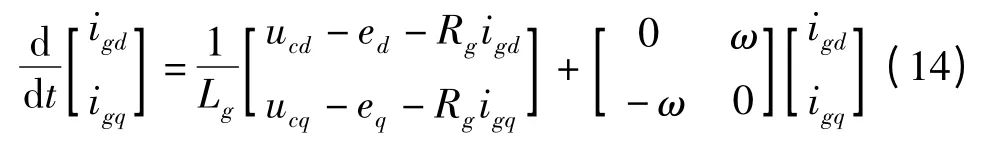
将式(10)进行旋转变换，可得:

将式(11)进行旋转变换，可得:

笔者对上式进行拉普拉斯变换，可得到模型在两相同步旋转坐标系下的复频域数学模型，如图2所示。

本研究通过框图等效变换原理［11］对模型进行解耦后的模型图如图3所示。

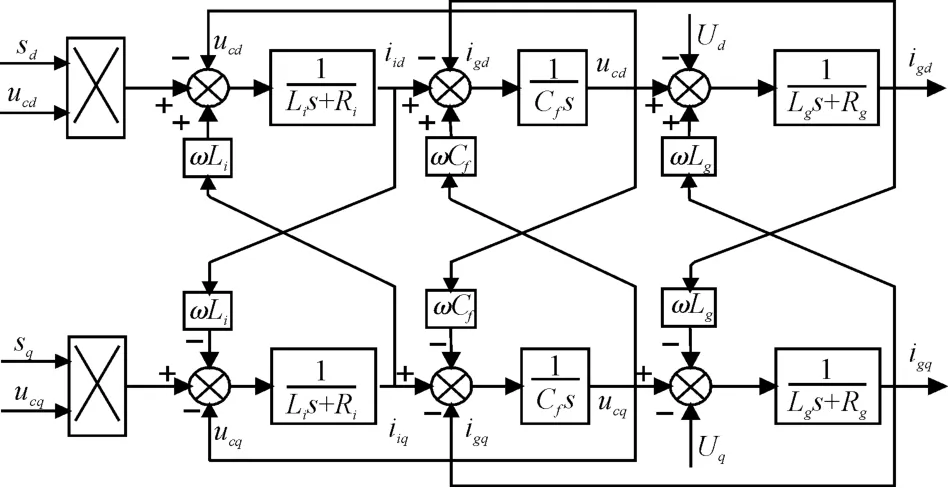
图2 旋转坐标系下的LCL 型有源逆变器数学模型

图3 LCL 滤波器完全解耦后化简框图模型

从图3 可以看出，d 轴和q 轴解耦后的模型框图完全对称，并且相互之间已经没有任何影响，其中解耦总项看作是干扰输入，故分析和控制其中一个轴即可，令d 轴作为有功功率控制轴进行讨论。

2 能量回馈系统的控制策略研究

2.1 基于有源阻尼的电流双环控制策略研究

常规的L 型能量回馈器一般采用单电流反馈控制，但是对于LCL 型能量回馈器只采用但电流反馈不能使系统稳定运行。LCL 型能量回馈器是三阶系统，由于滤波电容的存在会使系统在谐振频率处产生谐振尖峰，这样会导致系统工作不稳定。一般抑制谐振尖锋的方法是在电容支路串联电阻增加支路的阻尼，但是这种方法会增加系统的功耗，影响系统的效率。因此，针对单环控制系统存在谐振峰值的问题，本研究提出了通过电容电流反馈的方式增加系统的阻尼，即有源阻尼。相比于无源阻尼方式，有源阻尼一方面降低了能量损耗，另一方面也节省了成本;同时，引入电容电流的反馈控制还防止了网侧回馈电流滞后逆变侧电流的发生，提高了系统的功率因数［12］。其控制结构图如图4所示。

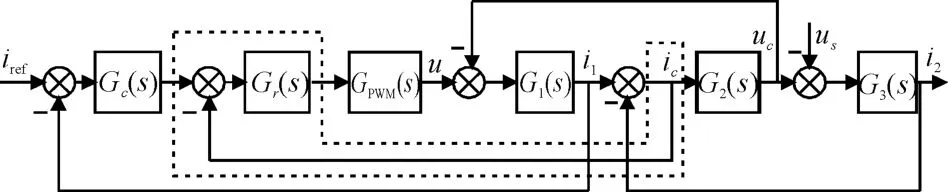
图4 电容电流有源阻尼控制框图

其中:Gr(s)=kcp;G1(s)=1/(Lis +Ri);G2(s)=1/Cfs;G3(s)=1/(Lgs +Rg);Gc(s)=kp+ki/s 是逆变侧电流反馈控制器，采用比例积分控制;GPWM(s)为逆变桥的等效传递函数，由于开关频率远大于基波频率，可以将逆变桥单元看成是一个相对于直流源的等效输出增益，即:

式中:Udc—直流侧电压;U'a—载波的幅值。

忽略电网电压us的干扰，为便于讨论忽略电感寄生电阻，系统的开环传递函数为:

其中:a4=LiLgCf，a3=(1 +kp)kcpkPWMLgCf;a2=kikcpkPWMLgCf+Lg+Li

分别代入Li、Lg、Cf、kPWM、kp、ki和kcp的值，利用Matlab 比较分析当系统加入电容电流有源阻尼比例反馈控制后频率特性曲线中谐振峰值的变化情况。系统的Bode 图如图5所示。

图5 电容电流有源阻尼控制系统频率特性图

比较两条对数幅相频率响应特性曲线明显可以看出，增加了电容电流反馈后，系统在谐振时的谐振尖峰基本完全消除，ζ ＞0.707，可看作是过阻尼系统，而且高频段和低频段的滤波效果完全没受影响;同时，相位也实现了超前校正，大幅提高了系统的截止频率ωc，从670 rad/s 增大到4 000 rad/s。

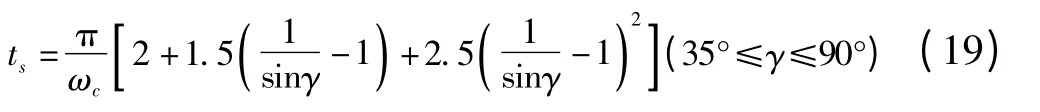
由式(19)可以看出当相位裕度γ 一定时，调节时间ts与截止频率ωc成反比，所以截止频率ωc增大，调节时间ts就会减小，从而增加了系统的快速性，网侧电流i2实现超前校正后，也减小了网侧电流对逆变侧电流的滞后相位。在系统的中频段，从图5 可以看出对数幅频特性曲线的斜率大概是－23 dB/dec 并且还占据了较宽的范围，这可以近似看作是一阶系统，几乎没有震荡，与G1曲线系统相比，G2曲线系统具有较高的平稳性;系统的相位裕度γ=45°，在合理的范围内，保证了系统的稳定性。

2.2 基于重复控制和电流双环控制的复合控制技术的研究

前面章节分析了基于电流双环控制的有源逆变系统，在忽略电网电压干扰的情况下，系统在电流双环控制下可以稳定、快速地高效工作。但是现实情况下，面对来自电网等其他外界的干扰，仅仅是基于dq 坐标系下PI 控制电流环和有源阻尼电容电流环的双环控制不能够保证系统正常、高效地工作，在此背景下提出了重复控制。周期性的波动产生的干扰可以通过重复控制器进行抑制;但是重复控制器的动态特性比较差，恰好PI 控制器具有较好的动态特性［13-14］，所以重复控制与PI 结合的复合控制可以实现互补。这样基于重复控制和电流双环控制的复合控制既可以使系统输出高质量波形又可以保证了系统具有良好的动态特性。基于重复控制和电流双环控制的复合控制系统框图如图6所示。

图6 基于重复控制和电流双环控制的复合控制框图

框图由重复控制器GRC(z)和电流双环控制系统Gp(s)两部分构成。

其中:

为便于分析用Gp(z)代替离散下的双环控制系统对象，则基于重复控制和电流双环控制的复合控制系统框图可化简为如图7所示。

图7 化简后的复合控制系统框图

通过以下几个方面对复合控制系统的性能进行分析。

2.2.1 系统稳定性分析

由图7 可以得到误差的表达式为:

由式(22～24)可得:

由上一节分析可知，被控制对象Gp(z)是稳定的，所以前向通道中1－Gp(z)也是稳定的。令Q(z)的取值小于1，则1－Q(z)z－N肯定也是稳定的。由上式可知，被控制系统达到稳定需要以下关系式:

系统的特征方程为:

解出方程(27)后就可以得到多个根，可以根据特征根的分布情况来判断系统是否是稳定的。当离散系统稳定的时候|zj| ＜1，zj为特征方程的一个根，则得出|zj|N＜1，根据稳定性判据，由特征方程变化可得下式:

则有:

即:

满足该条件可知系统肯定是稳定的。

式(30)还可以写成下面的形式:

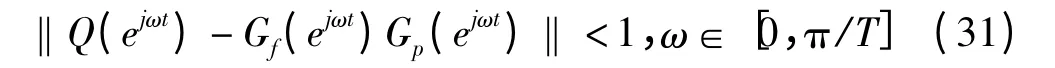
2.2.2 扰动抑制性分析

理想状态下，重复控制的扰动抑制性分析如下。

电网电压干扰与系统的误差关系为:

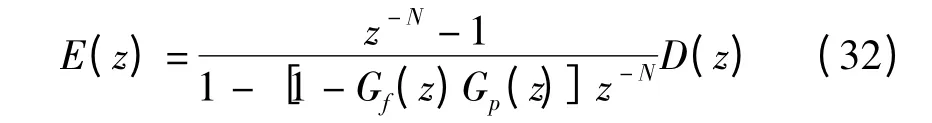
当扰动的角频率ωd是输入信号角频率ωr的整数倍关系时:

把式(33)代入式(32)中，得出系统在干扰下的误差是零。即理想条件下的重复控制可以抑制任何与输入频率成整数倍的扰动。

改进后的重复控制器对扰动的抑制能力如下面的分析。

电网电压干扰与系统的关系式为:

令:

把式(35)代入式(34)，得到:

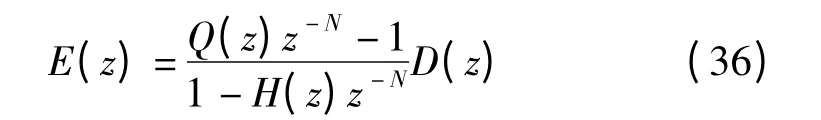
则误差的幅值特性为:

从上式可以看出，外界扰动引起的误差被削弱到原来的|Q(z)－1/(1－H(z))|倍，Q(z)值左逼近于1 时，误差会越来越小;Q(z)值右逼近于0 时，误差会更大。

2.2.3 收敛性分析

从式(29，35)可以推导出:

对于能量回馈有源逆变控制系统来说，其大部分的输入和扰动都是周期性重复的。

从式(39，40)可以得出，被控制系统的输入信号在一个周期内的幅值都会衰减H(z)，并且它的值越小其收敛的速度也就会更快。

H(z)=Q(z)－Gf(z)Gp(z)中补偿器Gf(z)在理想的状态下能够很好的对控制对象Gp(z)进行补偿，设置为Gp(z)的逆变换形式，并且Q(z)取值为1;那么H(z)的值这个时候就会变成零。换句话说就是基本上任何频率下的稳态误差都会很快逐渐的衰减为零。但是实际情况下，被控制系统不能实现稳态误差全为零的理想结果。

原因有很多，首先是Q(z)的取值大小不能选择为1［15］，否则系统会有处于临界稳定的风险。其次补偿器也不可能与被控制对象完全对消。再次，波动引起的干扰有时候也不能保证一直是周期性的。基于以上几个原因，现实情况下的重复控制系统和理想状态是不能完全相同的或者比理想状态下的收敛性好。但是从总体上来看，仍然是H(z)的值越小，能量回馈系统函数的收敛速度越快。

2.3 重复控制器参数的设计

由重复控制器的结构可知，重复控制器的设计主要有滤波器Q(z)、周期延迟系数和二阶补偿器Gf(z)等环节的设计。

2.3.1 Q( z)的设计

根据前面的分析可知，Q(z)对系统性能的影响表现为Q(z)的取值［16］:补偿器Q(z)的取值越小，就会使系统的抗干扰性更好，但是系统误差精度会有所下降;补偿器Q(z)的值越大系统稳态误差越高，但是系统的鲁棒性就越差。所以Q(z)的值的选择要综合考虑系统的干扰抑制性和误差精度两部分［17］。最终经过仿真分析，综合考虑各方面因素，本研究选择Q(z)的值为0.85。

2.3.2 周期延迟系数的选择

系统的开关频率为10 kHz，三相电网电压频率和能量回馈系统输出的电压频率都为50 Hz，每个基波采样拍数为:

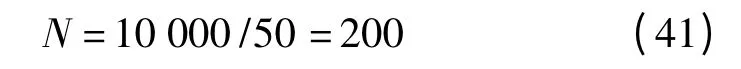
周期延迟系数一般去基波采样拍数，因此周期延迟环节设计为:

2.3.3 补偿器Gf( z)的设计

Gf(z)的设计非常重要，Gf(z)的主要任务就是对输出信号的相位和幅值进行偏差补偿。Gf(z)包括了3 个部分:重复控制增益Kr、相位补偿量zk和低通滤波器S(z)。

(1)Kr的取值

重复控制增益Kr的作用是进行幅值补偿。它的范围在Kr∈［0，1］。Kr的值会影响系统的动静态特性，增大Kr的值可以使系统的稳定性得到增强，但是系统的快速性降低;而减小Kr的值对提高系统的快速性有很大的作用［18］，但是系统的稳定性会降低。根据前面章节得到的控制对象的幅值特性，经过仿真分析，综合考虑选择Kr的取值为0.4。

(2)低通滤波器S(z)的设计

由于本研究设计的系统采用了有源阻尼电容电流环的电流控制，LCL 三阶有源逆变系统的输出信号中的谐振峰值已经被抑制掉，因此不需要再对谐振峰值进行抑制，只需高频信号进行衰减。在设计电流双环控制系统的控制参数时，本研究采用了极点配置的方法，忽略了系统中的非主导极点，只考虑了主导极点的作用，被控系统就转换成了二阶系统，因此把低通滤波器设计成二阶滤波器。

滤波器的表达式为:

滤波器的自然频率的大小一般要比空载时控制系统的谐振频率小［19］，比极点配置后的频率大。控制系统在空载的时候的谐振频率为:

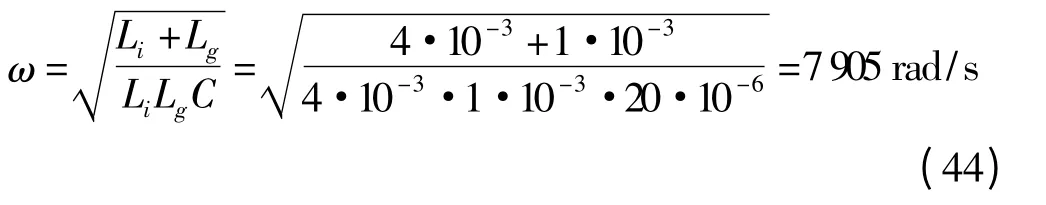
能量回馈系统在电流双环控制下极点配置后的自然频率为6 200 rad/s，在这里取7 000 rad/s 为它的自然频率。ξ 为系统的阻尼比，一般在ξ 为0.707 的时候能量回馈系统的性能相对较好，但是在实际的情况下，能量回馈系统还要考虑线路上的阻抗和自身存在的负载，所以ξ 取值的时候要考虑到这些方面的因素，经过综合分析取ξ 为0.6。

(3)超前环节zk的设计

经分析，被控对象和滤波器存在相位滞后，这是由低通滤波器引起的。与此同时，控制对象自身也有相位滞后的问题［20］，因此笔者利用超前环节zk对滞后的相位进行补偿。但是对k 值的大小的选择目前还仍然没有一个明确的方法，本研究经过综合的仿真分析比较最后选取k=4。

综上所述，可以得出重复控制器的表达式为:

给复合控制模块加入一个周期性随机谐波干扰信号如图8(a)所示。经过重复控制和电流双环控制的复合控制后的输出波形如图8(b)所示。很显然谐波干扰信号基本上被完全抑制掉，输出的波形的幅值在很短的时间内基本上趋于1 附近。这样就很好的实现了系统对谐波信号的完全消除，证明了复合控制技术对谐波抑制的有效性和优越性。

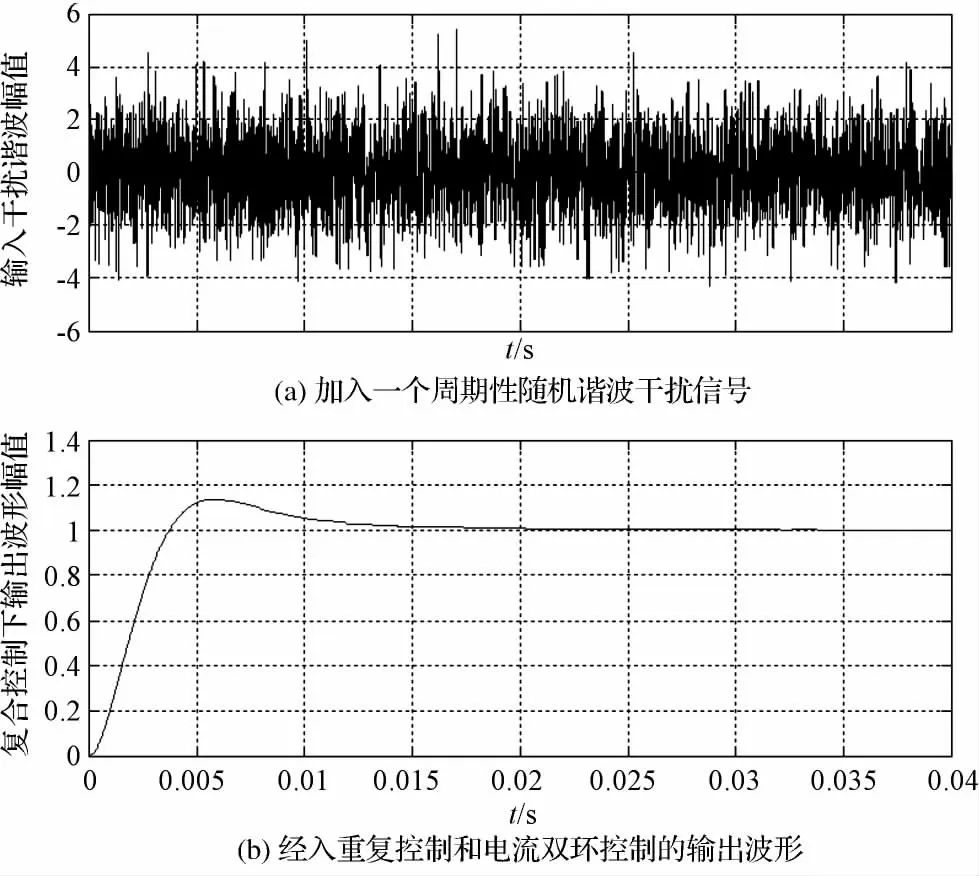
图8 复合控制模型在随机谐波干扰下的响应曲线

综上所述，系统将采用直流电压外环、基于重复控制和电流双环控制的复合控制下电流内环的控制策略。

3 仿真验证

为验证本研究控制方法下系统的动静态特性，笔者基于Matlab 仿真平台建立了系统的系统模型，仿真参数如下:系统功率为20 kW，额定电流为30 A，电网相电压220 V，直流电压600 V，开关频率为10 kHz，逆变侧电感为4 mH，滤波电容为20 μF，网侧电感为1 mH，Kp=1，Kcp=10，Ki=300。

根据前面章节所提到以及设计的参数，基于Simulink 对系统进行仿真，从以下两个方面对仿真结果进行分析。

3.1 系统输出电流所含谐波分析比较

电流双闭环控制与基于重复控制和电流双环控制的复合控制下能量回馈器回馈到电网中的电流的谐波含量如图9、图10所示。其中，电流双闭环控制下的输出电流谐波含量是4.33%，要比基于重复控制和电流双环控制的复合控制下的能量回馈器回馈到电网的电流谐波含量高。这说明复合控制可以使系统得到谐波含量更少的回馈输出电流。

图9 电流双环控制下输出电流谐波分析

3.2 复合控制下电网电压扰动仿真分析

给电网电压加入谐波扰动，在电流双环控制下输出电流谐波含量如图11所示。明显可以看出，输出电流波形谐波含量达到了7.98%，超出了合理范围，系统不能正常地工作。

图10 复合控制下输出电流谐波分析

图11 电流双环控制下输出电流谐波分析

基于重复控制和电流双环控制的复合控制系统的输出电流谐波分析图如图12所示。可以看出，输出电流波谐波含量降到了2.13%。显然加入电网电压前馈后，系统可以很好地抑制电网电压扰动的干扰。

4 结束语

在电流单环反馈控制的基础上，本研究加入了有源阻尼电容电流环，提高了系统的精确性和稳定性。针对电网电压的扰动干扰，本研究提出了重复控制和电流双环控制结合的复合控制技术。

采用重复控制和电流双环控制结合的复合控制技术的能回馈器具有以下特点:首先，可以保证系统具有较好的稳定性和快速性;其次，提高了能量回馈器的功率因数，增大了系统的转换效率;再次，系统对电网电压的扰动干扰，具有很好的抑制作用，增强了系统的鲁棒性。

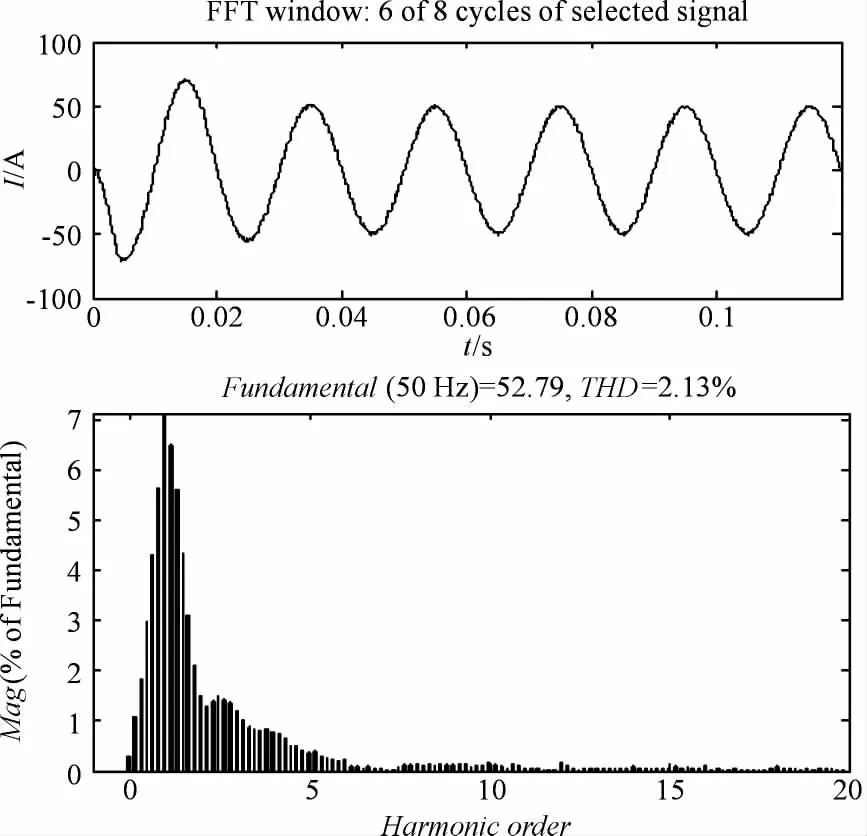
图12 电网电压前馈控制下输出电流谐波分析

［1］宋小亮，蔚 兰，陈国呈，等.基于直接电流控制的电机能量回馈器研究［J］.电力电子技术，2010，44(5):49-51.

［2］张钦军.基于单片机的电动车能量回馈控制策略分析［J］.机电工程技术，2012(6):36-38.

［3］葛 昂.带有LCL 滤波器的变频能量回馈并网控制策略研究［D］.天津:天津大学电气与自动化工程学院，2011.

［4］钱伯章.世界能源消费现状和可再生能源发展趋势［J］.节能与环保，2006(3):8-11.

［5］DANNEHL J，WESSELS C.Limita-tions of voltage-oriented PI current control of grid-connected PWM rectifiers with lCL filters［J］.IEEE Transactions on Industrial Electronics，2009(56):380-388.

［6］OYARBIDE E，GALARZA J，AURTENECHEA S，et al.Second-order predictive direct control of avoltage source inverter coupled to an LC filter［J］.IET Power Electronics，2007，1(1):38-49.

［7］ZHANG Ming，LI Bin，HANG Li-jun，et al.Performance study for high power density three-phase vienna PFC rectifier by using sVPWM control method［J］.IEEE Transactions on Industrial Electro-nics，2012(56):1187-1191.

［8］SHI Lei，XU Hai-ping，LI Dong-xu，et al.A novel high power factor PWM rectifier inverter for electric vehicle charging station［J］.IEEE Transactions on Industrial Electronics，2011(56):1-6.

［9］MALINOWSKI M，STYNSKI S，KOLOMYJSKI W，et al.Control of three-level PWM converter applied to variablespeed-type turbines［J］.Industrial Electronics，IEEE Transactions on，2009，56(1):69-77.

［10］许津铭，谢少军，肖华锋.LCL 滤波器有源阻尼控制机制研究［J］.中国电机工程学报，2012，32(9):27-33.

［11］包献文，卓 放，谭佩喧.三相LCL 型并网逆变器的模型分析及解耦控制［J］.西安交通大学学报，2014，48(2):44-49.

［12］王要强，吴凤江，孙 力.并网逆变器用LCL 滤波器新型有源阻尼控制［J］.电力自动化设备，2011，31(5):75-79.

［13］陈 东.并网逆变器系统中的重复控制技术及其应用研究［D］.杭州:浙江大学电气工程学院，2013.

［14］斯 然，吕征宇.LCL 型并网逆变器中重复控制方法研究［J］.中国电机工程学报，2010，30(27):69-75.

［15］HORNIK T，ZHONG Q C.A current-control strategy for voltage-source inverters in microgrids based on and repetitive control［J］.Power Electronics，IEEE Transactions on，2011，26(3):943-952.

［16］JAMIL M，SHARKH S M，ABUSARA M，et al.Robust Repetitive Feedback Control of a Three-phase Grid Connected Inverter［C］.Power Electronics，Machines and Drives(PEMD2010)，5th IET International Conference on Brightow:［s.n.］，2010:1-6.

［17］MORENO J C，HUERTA J M E，GIL R G，et al.A robust predictive current control for three-phase grid-connected inverters［J］.Industrial Electronics，IEEE Transactions on，2009，56(6):1993-2004.

［18］WU M，ZHOU L，SHE J.Design of observer-based robust repetitive-control system［J］.Automatic Control，IEEE Transactions on，2011，56(6):1452-1457.

［19］王汝田，王建赜，谭光慧，等.基于重复控制的新型三相变换器研究［J］.电力自动化设备，2009，28(6):11-16.

［20］SHE J，ZHOU L，WU M，et al.Design of a modified repetitive-control system based on a continuous-discrete 2D model［J］.Automatica，2012，48(5):844-850.