基于客观性权重的PPP 项目0 -1整数规划多目标决策

刘荣自，吴书安，史晓燕

(扬州职业大学，江苏 扬州 225009)

PPP 融资模式(Public-Private Partnerships)，因政府参与其全过程经营的特性而受到国内外广泛关注，将公共部门和私人部门以伙伴关系结合到一起，并将部分政府责任以特殊形式(特许经营权)转移给社会主体(企业)。政府与企业共同合作、利益共享、风险共担。政府依赖企业减轻财政负担，企业也因政府的参与而风险系数大幅降低。由于政府以社会效益最大化为价值取向，而企业以自身经济效益最大化为终极奋斗目标，因此，造成这些参与方目标定位的大不同，使得项目决策无形中增大了难度。

对于PPP 项目融资决策类问题，目前采用的方法主要包括运用权重敏感性分析的方法分析权重的变化，进而确定PPP 项目的最优决策，但由于无法归纳出数学模型公式，使得问题的解决不具一般性［1］;运用实物期权理论建立数学模型进行评价研究解决对PPP 项目融资决策问题，但并没有针对PPP 项目特有的多个目标从目标层次去分析进而决策［2］;建立一种模型，有利于政府和企业合作投资使项目风险性降低，但却没有给出最优方案选取的方法［3］。如果分析透彻效益主体，把目标属性合理归类统一，也可以为最优方案的选取提供一种较合理的方式。本文从PPP项目各目标属性的类型出发，建立了适用于PPP项目融资决策的赋予权重的0 -1 整数规划数学模型。

1 PPP 项目决策多目标0 -1 规划数学模型

1.1 目标类型的统一化

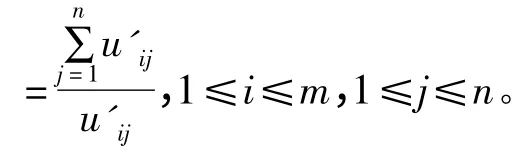
进而得新矩阵

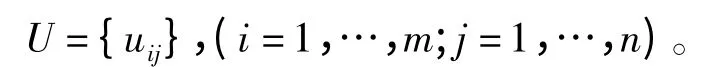
1.2 模型的建立

首先假设PPP 项目决策时各重要属性值αi均可量化，且围绕某一特定值波动，对各属性进行量化，然后将各方案进行排序，由前述可得选定取值最大者即为最优方案。并且设定进行风险投资前先预知每个方案αi各个属性值fi的准确赋值，因此对于一般的PPP 项目，令

由前述，目标类型统一化后的矩阵为:U ={uij}，(i=1，…，m;j=1，…，n)，

可得PPP 项目决策多目标0 -1 规划模型为:

该模型相应满足各目标属性利润总和最大化的要求，由于其典型的多目标性，赋予各目标客观性权重以方便求解。

1.3 客观性权重的确定

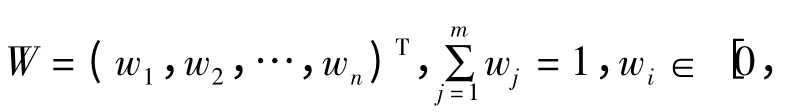
2 仿真算例

某地拟建一水坝项目，采用PPP 模式，拟采用限额设计方式。该项目主要有旅游、发电、渔业、航运、防洪、灌溉等收益来源，共有5 个备选方案。收益来源记为(a1，a2，a3，a4，a5，a6)6 个属性，相应得到各方案的属性值见表1。

表1 各个方案对应的属性值

分析收益目标来源的本质，可得旅游、发电相关的属性值越大越好，为效益性目标;洪水量属性值越小越好，为成本性目标;而渔业、航运、灌溉量均有一个最佳值，为固定性目标，但是由于这个固定值不影响min，max 的取值，故而可以忽略不计。从而可得该PPP 项目0-1 整数规划模型为:

使用MATLAB 多目标优化工具［5］箱求解器，编写目标函数的M 文件myfun0. m，根据该PPP项目自身属性特点，赋予客观性权重，并给出初值。

计算结果为:X=(0，0，0，0，1)T，因此根据此结果给出的建议是优先选择第5 个方案，整个求解过程简单、方便。从实际操作的角度显示了模型的可操作性。该方法相比于文献［1］中给出的方案，更显简单、直观和明确。MATLAB 多目标优化工具箱应用于PPP 项目是一种新的尝试，还需要更多的实践反馈来改进完善。

3 结语

PPP 模式将政府资金与企业资金结合在一起，两大投资主体之间相互取长补短，发挥各自优势，进行风险分担。由于项目两大参与方(政府与企业)收益来源目标定位不同甚至差异巨大，导致决策过程复杂甚至难以为继，之前学者提供的方法多数流于表面，不具备一般性。在这个前提下，本文建立了PPP 项目决策的多目标0 -1整数规划模型。MATLAB 多目标优化工具箱对于客观性权重的成果运用，为方案决策提供了一种新方法。当方案目标属性确定后，运用文中提出的方法，可以很快求得一个较好方案。相比其它方法，更加明确和直观。这是解决PPP 项目决策问题的一次创新，为PPP 项目多方案决策问题开辟了一个新的解决途径。

［1］ 韩亚品，蒋根谋.基于权重敏感性分析的PPP 项目多目标决策分析［J］.商场现代化，2009(12):33.

［2］ 杨璐. 基于实物期权的PPP 项目投资决策研究［D］.杭州:浙江大学，2008.

［3］ 黄怿炜.PPP 项目评价方法与决策研究［D］.上海:同济大学，2007.

［4］ 李柏年.多目标决策中客观性权重的一种确定法［J］.运筹与管理，2002，11(5):37 -38.

［5］ 苏金明，张莲花，刘波. MATLAB 工具箱使用［M］.北京:电子工业出版社，2004.