预应力锚索损伤软化精细有限元模型

张 雄，陈胜宏

（1.中国水电工程顾问集团有限公司，北京 100120；2.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072）

1 引 言

预应力锚索通过钻孔将钢筋、钢绞线或高强度钢丝固定于深部稳定的地层中，并在被加固体表面通过张拉产生预应力，从而达到使被加固体稳定和限制其变形的目的[1]。因其经济合理、安全可靠、对岩土体扰动小、施工快捷等优点而被广泛应用于岩土体的加固工程中[2]。

锚固段是预应力锚索主要受力结构，其依靠钢筋或钢绞线与砂浆、砂浆与岩体孔壁的界面相互作用传递、转移巨大的锚固力。试验研究表明，大多数的预应力锚固的失效是发生在钢绞线-砂浆、砂浆-围岩体接触面上，接触界面是锚固系统的薄弱环节。接触面上两种材料变形不一致、粘结强度较弱、韧性较低，导致失效极易发生在界面上[3]。目前对于锚固段接触面应力规范[4]还是假设锚固段剪应力沿锚固段呈均匀分布。但除了土体、砂层、软岩等岩土体中，锚固段剪应力分布不均匀性已得到普遍认可，也通过试验得到验证，其分布形式如图1 所示，有A、B、C 3 种模式[5-7]。目前大都是独自研究一个单独模式，笔者认为，锚固段的应力分布其实是动态变化的，在荷载较小的情况下或者端口处粘结较好时，接触面全长处于弹性状态，此时剪应力峰值在端口，如A 模式；当荷载逐渐加大时或端口处粘结较差时，接触面已经部分屈服，但还能承担部分剪应力，峰值转移到里面，如B 模式；当荷载增大到接触面破坏时，端口已不能承担剪应力，所以为0，如C 模式，应力已逐渐转移到内部。尤春安[8]通过试验将锚固体界面上的变形分为弹性变形、塑性滑移变形和脱黏变形3个阶段验证了这一点。

目前还没有模拟成果能反映这一力学变化过程，有关锚固段的模拟大多较粗糙，因此，建立合理的界面模型研究岩体与灌浆体之间的力学行为，正确认识荷载传递机制，研究锚固段应力的分布规律，对于预应力锚固设计和应用具有极其重要的意义。

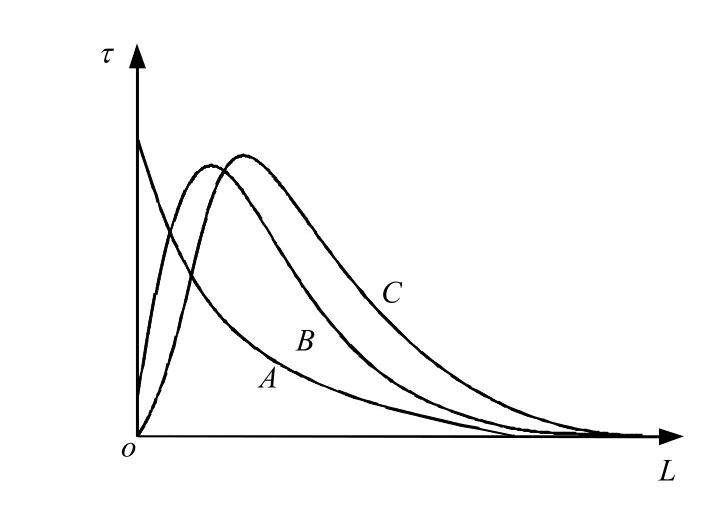
图1 剪应力分布形式示意图Fig.1 Distributions of shear stress

2 有关模拟锚固段接触面的讨论

如何正确地分析接触面上的受力变形机制、剪切破坏发展趋势、荷载传递过程，并在计算中加以正确地模拟，是锚固数值分析研究中的关键点。接触面的研究主要包含两个方面：一是接触面上的本构关系，尤其是剪应力和剪切变形之间的关系，以及接触面的错动、张开对其本构关系的影响；另一方面是接触面单元，它是数值分析中模拟接触面变形的一种特殊单元。这两方面的研究应该是互相联系、互相影响的，接触面本构关系是为了表达接触面上的变形，接触面变形的表示又要适应所选用的接触面单元。

在本构关系方面，Yazici[9]采用了粘结介质强度理论模型。该模型认为，界面的压力与砂浆的剪胀和径向位移有关。Hyett 等[10]根据介质破坏的摩擦-剪胀力学机制，讨论了砂浆和粘结界面变形破坏情况。伍国军等[11]根据锚固界面法向刚度服从指数分布的软接触型式，提出剪切面的非线性流变本构模型。

在接触单元方面，通常分为有厚度和无厚度模型。无厚度接触面单元充分考虑了相邻接触物体接触面间位移的不连续性。而薄层界面单元则相反，通过节点位移来插值构造单元内部位移场，认为相邻接触物体接触面的位移具有某种连续性。应用到预应力锚固界面分析中的有Goodman 单元、常规的薄层单元。张雄等[12]提出，用复合单元模型来研究内锚段，将接触单元隐含在常规有限元单元里面，避免了复杂的网格前处理，同时又可以保证计算精度。雷晓燕[13]以新接触摩擦单元直接取节点接触应力作为基本未知量，模拟两物体间的摩擦滑动、张开和闭合过程。

上述锚固数值分析方法多侧重于研究锚固体界面的滑移进行分析，模拟得也较为简单、粗糙。关于钢绞线、砂浆和岩体的共同作用变化过程，锚固体应力分布变化特征的研究有待深入。

3 接触面特性

一般采用界面的法向应力和剪应力以及界面位移约束来描述界面的滑移及开合状态，模拟钢绞线-砂浆、砂浆-围岩体之间的接触过程。他们之间的关系可以通过试验反映。

3.1 界面力学特性试验

尤春安[3]通过预应力锚索锚固段界面力学特性试验发现，锚固体界面层是具有一定厚度并具有特殊力学性质的材料，其力学性质与岩土体的性质相关。通过典型的拉拔荷载-位移曲线，如图2 所示，提出锚固段从加载到破坏分为弹性变形、塑性滑移变形和脱粘变形3个阶段，进而提炼出锚固段界面层的剪应力-位移本构关系，如图3 所示。（图2、3均引自文献[3]）

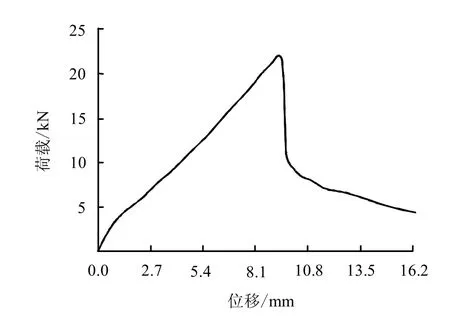
图2 荷载-位移曲线[3]Fig.2 Curve of load-displacement[3]

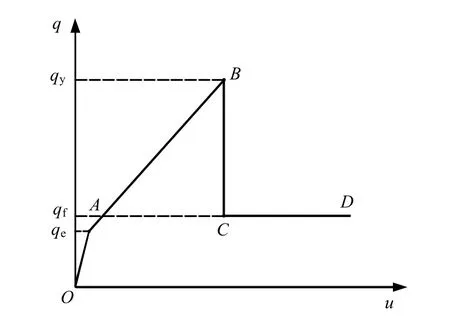
图3 荷载-位移本构关系[3]Fig.3 Constitutive relation of load-displacement[3]

3.2 接触面法向行为

当接触面的法向应力小于接触面的抗拉强度时，接触面为闭合状态，此时接触面传递法向应力。当接触面的法向应力大于等于接触面的抗拉强度时，接触条件从闭到开时，不传递法向应力，法向应力得到释放。

3.3 接触面切向行为

当接触面剪切应力达到临界剪应力值之前，不会发生切向运动；当等于或超过临界剪应力时，接触面之间会发生相对滑动。此时应力进行重新调整，峰值向内部转移。

接触面从稳定到滑移到失效的变化过程，实质是材料力学性能在外载的强迫作用下发生损伤劣化的过程。本文将采用钢绞线、砂浆及其相互接触面的有限元精细化模型，建立界面损伤软化精细模型，探索锚段应力分布及其传递变化规律，通过试验与数值分析对比，验证其合理性。有关这方面的报道还很少，本文试图在此进行一些有益的尝试。

4 接触面损伤软化本构模型建立

4.1 基本原则

接触单元由薄层实体和接触元件串联而成，见图4，具有以下两条基本原则：应变迭加原则，单元的应变增量等于实体与接触面的应变增量之和；应力-致原则，单元、实体块和接触面的应力增量相等[14]。下面的公式可参考文献[14]。

在有限元计算中，这两条原则可分别表示如下（小写字母下标表示在局部坐标下的量，大写字母下标表示在整体坐标下的量，不带下标则表示等效后的接触单元的量）：

（1）应变迭加原则

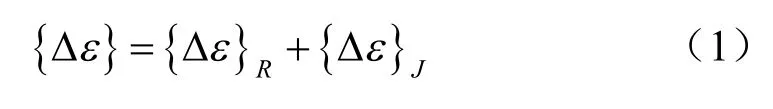
式中：R为实体元件；J为接触元件。

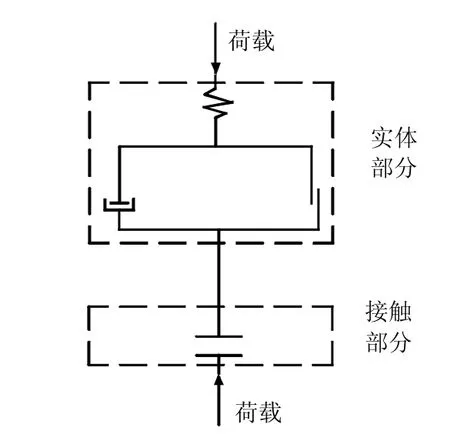
图4 接触单元模型Fig.4 Contact element model

（2）应力一致原则

定义整体坐标和局部坐标下的应力和应变相互转换关系为

式中：[T]j为整体局部坐标转换矩阵。

根据弹黏塑性势理论，各组成元件的弹黏塑性本构关系均可写为

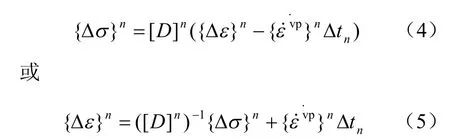
式中：Δtn是在时间 tn的时步长；[D]、分别是弹性矩阵、黏塑性应变率；n为时步。

4.2 损伤变量的选取

根据弹黏塑性势理论，Δt时步内的黏塑性应变增量为

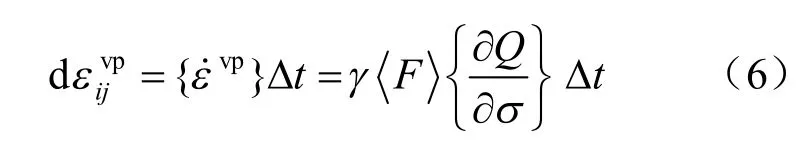
式中：Q为黏塑性势函数，当F=Q时，称黏塑性流动是关联的，否则为非关联；F为屈服开关函数，为流动参数。

于是，黏塑性体积应变增量为

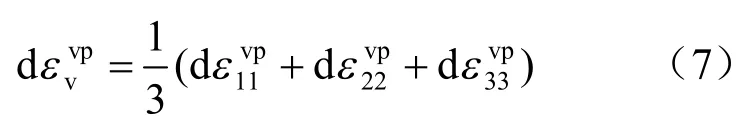
黏塑性偏应变增量为

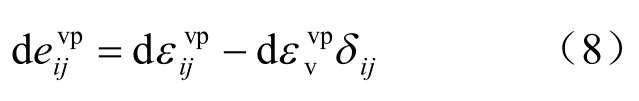
应变偏量的3个不变量分别为

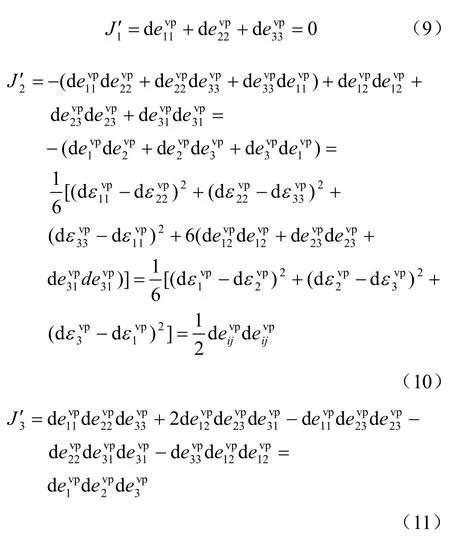
于是，等效黏塑性偏应变增量可以写为

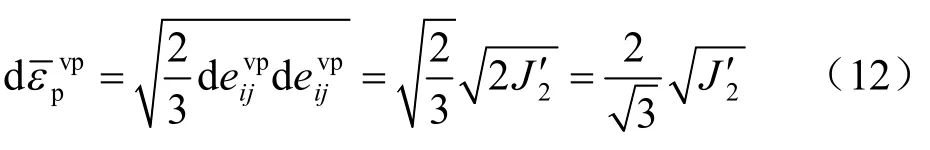
因此，累积黏塑性体积应变、累积等效黏塑性偏应变分别为（文中的一些推导可以参考文献[15]）

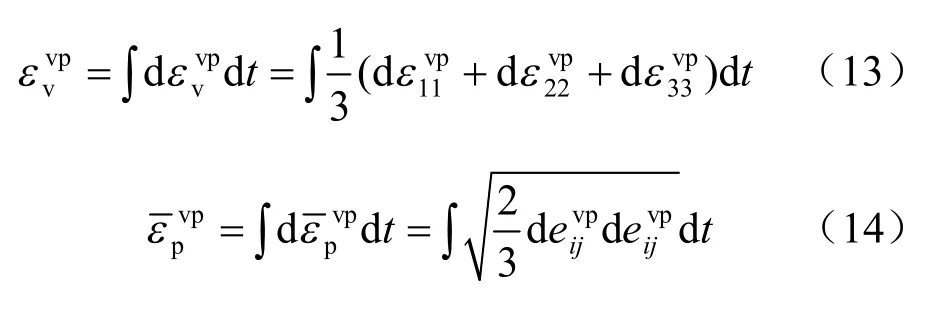
通常，在实际锚固工程中接触面会在外载的作用下受到不同程度的损伤，其材料性质在一定程度上的弱化可以采取一些指标进行衡量，主要体现为法向刚度Kn、切向刚度Ks、弹性模量E、摩擦角φ、凝聚力c、流变系数γ 的降低和泊松比μ 的升高。一般而言，接触面材料性质在外载作用下会随着时间发生变化的，具体表现为弹性指标、强度指标和流变参数的逐步劣化。

周华[16]利用取累积等效黏塑性偏应变研究了岩体松弛岩体力学参数的损伤及演化。本文在此基础上将其拓展到接触面力学参数损伤软化上，可以将接触面各力学参数变化的具体形式写为（本文只列出法向刚度、切向刚度的参数变化推导过程，其他的如弹性模量、泊松比、凝聚力、内摩擦角和流变系数依次类推）：

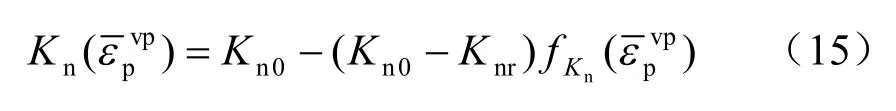
式中：Kn0、Ks0分别为接触面初始状态的法向刚度、切向刚度；Knr、Ksr为接触面损伤后残余状态的参数；为一定累积等效黏塑性偏应变下接触面损伤后的力学参数；分别为力学参数随累积等效黏塑性偏应变单调递增的函数，可以采用线性函数或其他非线性函数。

引入损伤的概念，则参数变化的具体形式可写为

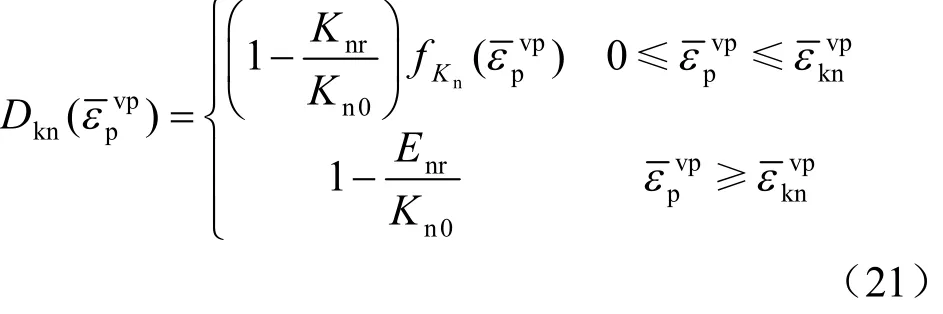
若损伤接触面各力学参数随累积等效黏塑性偏应变单调递增的函数均采用线性函数，则法向刚度、切向刚度损伤变量与等效黏塑性偏应变的关系曲线如图5～7 表示。

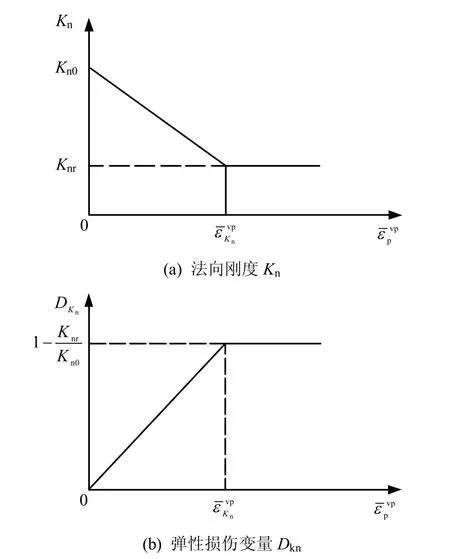
图5 法刚及其损伤变量与等效黏塑性偏应变关系曲线Fig.5 Curves of normal stiffness and its damage variableequivalent viscoplastic deviator strain.

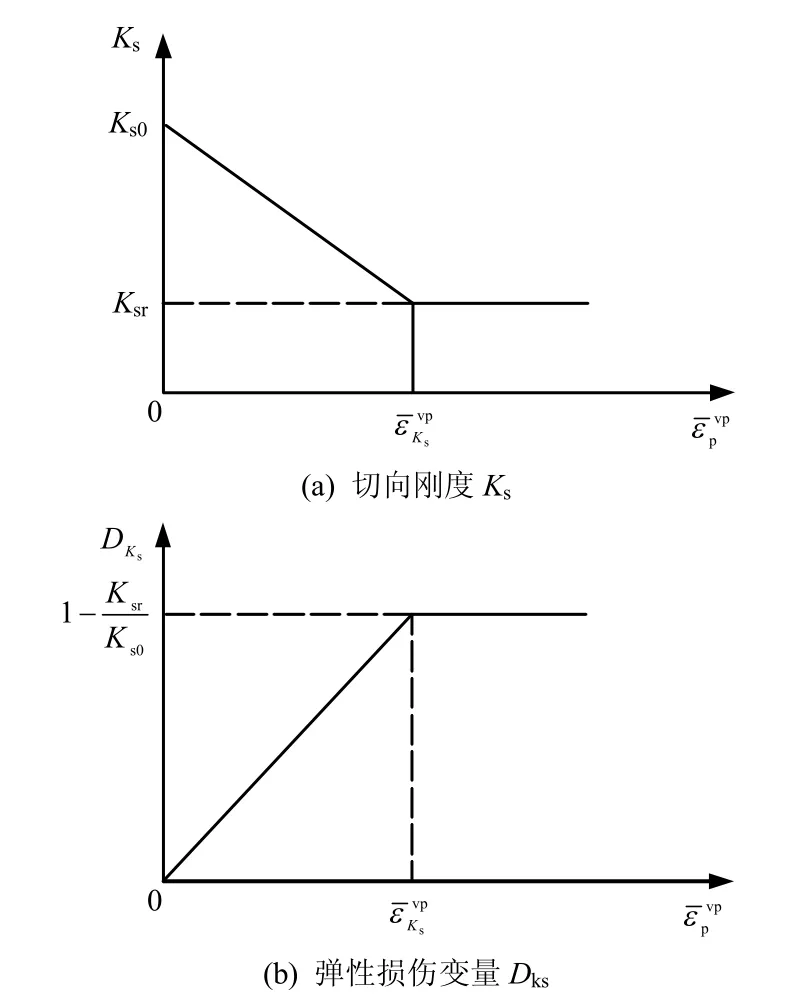
图6 切向刚度及其损伤变量与等效黏塑性偏应变关系曲线Fig.6 Curves of shear stiffness and its damage variableequivalent viscoplastic deviator strain

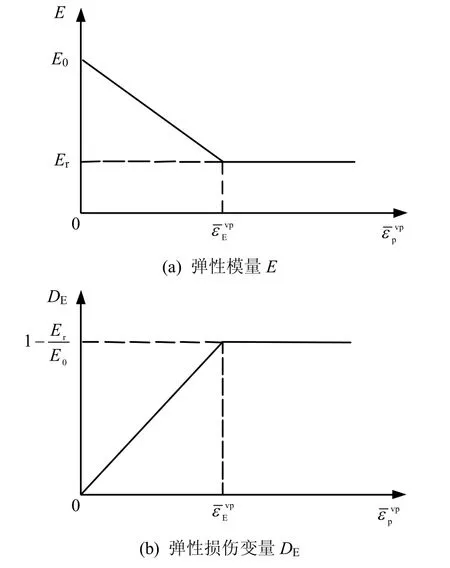
图7 弹性模量及其损伤变量与等效黏塑性偏应变关系曲线Fig.7 Curves of elastic modulus and its damage variableequivalent viscoplastic deviator strain

4.3 弹黏塑性损伤本构模型

对实体和接触元件分别进行具体化，接触面进入塑性阶段后，某时刻损伤后的本构关系如下：

4.3.1 实体元件的本构关系

弹性矩阵可表示为

采用Drucker-Prager 屈服准则：

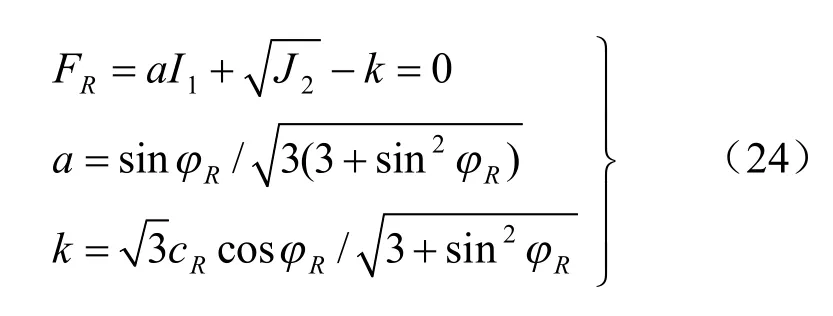
式中：φR、cR分别为内摩擦角、凝聚力。

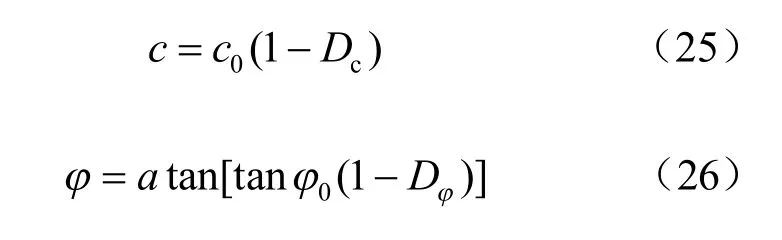
假定关联流动法则成立，即

则黏塑性应变率为

式中：γR为流动参数。

4.3.2 接触元件的本构关系

弹性矩阵：

式中：knj=Kn0(1-Dkn)、ksj=Ks0(1-Dks)分别为法向和切向刚度系数。

黏塑性应变率为

屈服函数取Mohr-Coulomb 模型：

式中：cj、φj分别为凝聚力、内摩擦角；γj为流动参数，形式分别如式（25）、（26）、（29）。

4.3.3 单元的本构关系

将式（31）、（28）代入式（1），即可得到接触单元的本构方程：

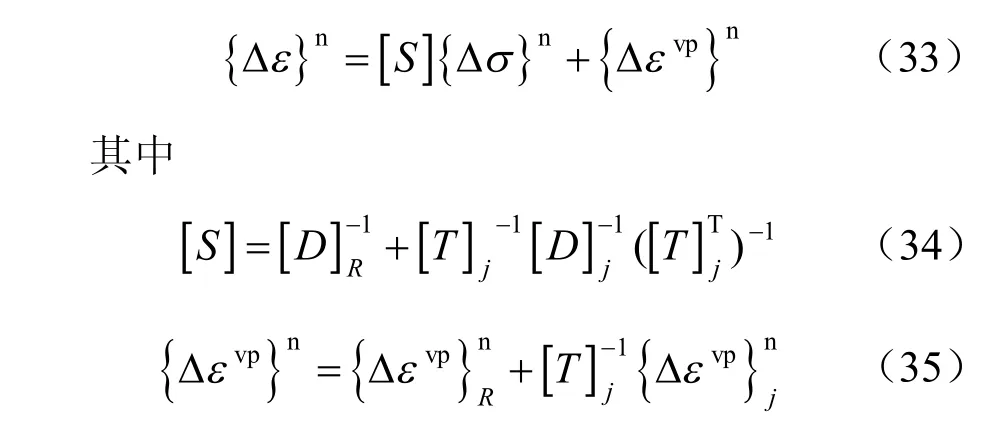
5 算例分析

顾金才等[17]对预应力锚索内锚固段受力进行了现场试验，采用该试验进行数值模拟对比。取尺寸5 m×5 m×5 m 的立方体进行分析。表1为试验参数，表2为注浆材料力学指标。张拉步骤：先用小千斤顶进行3 次单根循环张拉，每次荷载增量ΔP=120 kN(6×20 kN)，然后使用大千斤顶进行整体张拉，整体张拉的第一级荷载P=400 kN，以后每级荷载增量为ΔP=50 kN，I号锚索最大张拉荷载为1 000 kN。

表1 试验锚索编号及其主要特征Table 1 Numbering and main characteristics of cable

表2 注浆材料主要力学指标Table 2 Mechanical parameters of grouting materials

图8为钢绞线布置图。图9为有限元网格，共有21 925个单元，20 520个节点。表3为实体材料力学参数。表4为接触面力学参数。有限元接触面是用含有1 mm 的接触单元模拟的。

表3 材料的力学参数Table 3 Mechanical parameters of materials

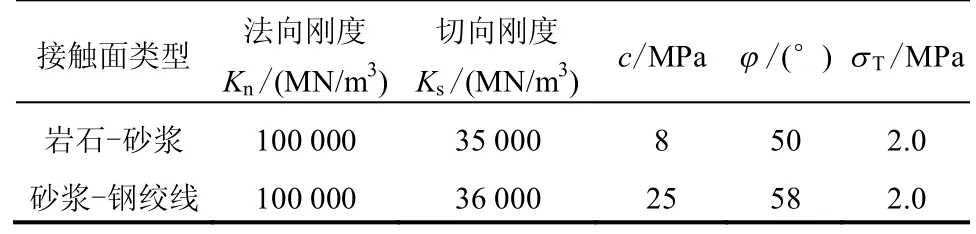
表4 接触面的力学参数Table 4 Mechanical parameters of interfaces

图8 钢绞线布置图Fig.8 Distributions of steel stranded wires

图9 有限元网格Fig.9 FE meshes

图10为接触面剪应力沿锚固段长度分布试验值，从试验值可以看出，注浆体与岩体之间接触面在距端口0.25 m 处出现一定程度的损伤软化，在数值分析计算中认为此部分随着荷载加大到400 kN，其材料参数不断损伤软化。0～0.1 m 处材料强度参数降到0，0.1～0.2 m 处材料强度参数降到1/2，0.20～0.25 m 处材料强度参数降到1/3，各参数等效黏塑性偏应变阀值均取为1.0×10-3。图11、12为有限元数值模拟的计算结果，从图中可以看出，数值分析反映的锚固段应力变化规律与试验基本一致，且具有以下特点：

（1）注浆体与钢绞线之间的剪应力分布特点

剪应力在内锚段端口呈现峰值，往里呈指数型衰减，峰值剪应力为平均剪应力的8～10 倍，分布范围集中在距端口2 m 内。峰值没有随着荷载的增大往里衰减，说明注浆材料与钢绞线粘结效果较好。

图10 接触面剪应力沿内锚段长度分布状态试验值Fig.10 Shear stress of interface along the anchoring segment for prestressed anchor cable(test)

图11 接触面剪应力沿内锚段长度分布有限元值Fig.11 Shear stress of interface along the anchoring segment for prestressed anchor cable(FEM)

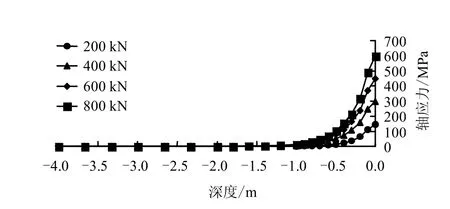
图12 1#钢绞线轴应力沿内锚段长度分布有限元值Fig.12 Axial stress of steel stranded wires 1# along the anchoring segment for prestressed anchor cable(FEM)

（2）注浆体与岩体之间的剪应力分布特点

注浆体与岩体之间的剪应力分布也是不均匀的，在内锚段端口附近有高度的剪应力集中，其峰值剪应力可大平均剪应力的4～8 倍。剪应力的分布范围集中在距端口2 m 内，剪应力峰值和分布范围随着锚索张力的增大而增大。但峰值点的位置和损伤长度几乎不变，说明距端口0.25 m 处注浆材料与岩体粘结效果没有里面好。

（3）钢绞线轴应力分布特点

钢绞线的轴应力分布也是不均匀的，与注浆体和钢绞线接触面剪应力的分布形式相似，峰值随深度增加急剧减小，轴应力的分布范围集中在距端口2 m 内，轴应力峰值和分布范围随着锚索张力的增大而增大，当超过2 m 后应力分布不明显，几乎为0。

5 结 语

本文建立了包含钢绞线、砂浆、接触面的损伤软化精细有限元模型，研究锚固段应力分布变化过程。该模型优点是精细地描述了钢绞线、砂浆和接触面等结构的力学行为，可以反映接触面力学材料损伤软化过程，更加符合实际情况，常规有限元难以体现这一变化过程。为检验其正确性，与现场试验进行了对比，结果显示，计算分析反映的锚固段应力变化规律与试验基本一致。随着荷载不断加大，锚固段接触面上的剪应力峰值由端口往里转移。当端口处于弹性阶段峰值在端口，呈指数衰减模式；当端口处出现损伤软化，峰值往里转移。

[1]杨晓东.锚固与注浆手册[M].北京:中国电力出版社,2009.

[2]何君弼.“八五”攻关预应力群锚加固边坡机理研究[J].建筑技术开发,1997,24(2):9-12.HE Jun-bi.Mechanism study of strengthening slope with prestressed multi-bolts[J].Building Technology Development,1997,24(2):9-12.

[3]尤春安.预应力锚索锚固段界面滑移的细观力学分析[J].岩石力学与工程学报,2009,28(10):1976-1985.YOU Chun-an.Analysis of interfacial slip mesomechanics in anchorage section of prestressed anchor cable[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):1976-1985.

[4]中华人民共和国国家发展和改革委员会.DL/T5083-2004 水电水利工程预应力锚索施工规范[S].北京:中国电力出版社,2004.

[5]PHILLIPS S H E.Factors affecting the design of anchorages in rock[R].London:Cementation Research Ltd,1970.

[6]张发明,刘宁,赵维炳.岩质边坡预应力锚固的力学行为及群锚效应[J].岩石力学与工程学报,2000,19(增刊1):1077-1080.ZHANG Fa-ming,LIU Ning,ZHAO Wei-bing.Mechanical behaviour and effects of prestressed anchorage for rock slope[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(Supp.1):1077-1080.

[7]蒋忠信.拉力型锚索锚固段剪应力分布的高斯曲线模式[J].岩土工程学报,2001,23(6):659-662.JIANG Zhong-xin.A Gauss curve model on shear stress along anchoring section of anchoring rope of extensional force type[J].Chinese Journal of GeotechnicalEngineering,2001,23(6):659-662.

[8]尤春安.预应力锚索锚固段界面滑移的细观力学分析[J].岩石力学与工程学报,2009,28(10):1976-1985.YOU Chun-an.Analysis of interfacial slip mesomechanics in anchorage section of prestressed anchor cable[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):1976-1985.

[9]YAZICI S.Damage mechanics around a tunnel due to incremental ground pressure[J].International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts,1997,34(3,4):655-627.

[10]HYETT A J,BAWDEN W F,MACSPORRAM G R,et al.A constitutive law for bond failure of fully ground cable bolts using a modified Hoek cell[J].International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts,1995,32(1):11-34.

[11]伍国军,陈卫忠,贾善坡,等.岩石锚固界面剪切流变试验及模型研究[J].岩石力学与工程学报,2010,29(3):520-527.WU Guo-jun,CHEN Wei-zhong,JIA Shan-po,et al.Shear creep experiments for anchorage interface mechanics and nonlinear rheological model of rocks[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):520-527.

[12]张雄,陈胜宏.预应力锚索内锚段复合单元模型研究[J].岩土力学,2012,33(3):933-938.ZHANG Xiong,CHEN Sheng-hong.Composite element model research on inner anchoring section of prestressed anchor cable[J].Rock and Soil Mechanics,2012,33(3):933-938.

[13]雷晓燕.三维锚杆单元理论及其应用[J].工程力学,1996,13(2):50-60.LEI Xiao-yan.Formulation and application of 3D anchor bolt elements[J].Engineering Mechanics,1996,13(2):50-60.

[14]陈胜宏.计算岩体力学与工程[M].北京:中国水利水电出版社,2006.

[15]郑颖人,孔亮.岩土塑性力学[M].北京:中国建筑工业出版社,2010.

[16]周华.岩体开挖损伤松弛机理与分析[D].武汉:武汉大学,2010.

[17]顾金才,明治清,沈俊,等.预应力锚索内锚固段受力特点现场试验[C]//岩土锚固新技术.北京:人民交通出版社,1998:109-114.